本記事の内容
本記事は、準同型写像、同型、核(kernel)について解説する記事です。
本記事を読むにあたり、群、部分群、正規部分群について知っている必要があるため、以下の記事も合わせてご覧ください。
↓群の記事
↓部分群、正規部分群の記事
群、部分群、正規部分群の軽い復習
群、部分群、正規部分群を軽く復習します。
群とは?
群
\(G\)を空でない集合とする。\(G\)上の演算\(\varphi:G\times G\longrightarrow G\)が定められていて、次の性質を満たすとき、\(G\)を群(group)という。- 結合律 任意の\(a,b,c\in G\)に対して、\(\varphi\left(\varphi(a,b),c \right)=\varphi\left(a,\varphi(b,c) \right)\)が成り立つ。
- 単位元の存在 ある\(e\in G\)が存在して、任意の\(a\in G\)に対して\(\varphi(a,e)=\varphi(e,a)=a\)が成り立つ。この\(e\in G\)を単位元と呼び、\(1_G\)と書くことがある。
- 逆元の存在 任意の\(a\in G\)に対して、ある\(b\in G\)が存在して、\(\varphi(a,b)=\varphi(b,a)=e\)が成り立つ。この\(b\in G\)を\(a\in G\)の逆元といい、\(a^{-1}\)で表す。
演算\(\varphi:G\times G\longrightarrow G\)に対して
$$
\varphi(a,b)=ab
$$
と書くことにすると、
群(簡易的な記法を使ったver.)
\(G\)を空でない集合とする。\(G\)上の演算が定められていて、次の性質を満たすとき、\(G\)を群(group)という。- 結合律 任意の\(a,b,c\in G\)に対して、\(\left(ab \right)c=a\left(bc \right)\)が成り立つ。
- 単位元の存在 ある\(e\in G\)が存在して、任意の\(a\in G\)に対して\(ae=ea=a\)が成り立つ。この\(e\in G\)を単位元と呼び、\(1_G\)と書くことがある。
- 逆元の存在 任意の\(a\in G\)に対して、ある\(b\in G\)が存在して、\(ab=ba=e\)が成り立つ。この\(b\in G\)を\(a\in G\)の逆元といい、\(a^{-1}\)で表す。
以降、断りがない限り、演算\(\varphi:G\times G\longrightarrow G\)の演算結果を\(\varphi(a,b)=ab\)で表すことにします。
詳しくは、【代数学の基礎シリーズ】群論編 その1を御覧ください。
部分群とは?
部分群
\(G\)を群、\(H\subset G\)とする。\(H\)が\(G\)の演算によって群になるとき、\(H\)を\(G\)の部分群(\(H\) is a subgroup of \(G\))という。部分群を一言で述べれば、
でした。
正規部分群とは?
正規部分群
\(H\)を\(G\)の部分群とする。任意の\(g\in G\)、任意の\(h\in H\)に対して、\(ghg^{-1}\in H\)となるとき、\(H\)を\(G\)の正規部分群(normal subgroup of \(G\))という。またこのとき、\(H\triangleleft G\)、あるいは\(G\triangleright H\)と書く。準同型写像
群と群との間の写像で、かつ特別な性質を持つ写像を準同型写像といいます。
準同型写像は、2つの群\(G_1\)、\(G_2\)が与えられたとき、\(G_1\)と\(G_2\)が本質的に同じモノかどうかということを定式化するために必要です。
群は集合ですが、単なる集合ではありません。
その集合に定められている演算が群の構造を決めます。
つまり、2つの集合の要素は全て同じだったとしても、それぞれに定められている演算が異なれば群としては異なります。
従って、2つの群を比べるとしたらば、単に集合として対応しているだけでは不十分で、演算も対応している(演算が等しくなくても良いですが、演算にも対応がある、という意味)ようなモノを考えなければなりません。
その対応(つまりは写像)が準同型写像です。
「準同型写像」を一言で。
準同型写像を一言で述べれば
です。
「”群の構造を保つ”ってどういうこと?」となるかと思いますが、直感的には、先に述べたとおり、単に群が集合として対応しているだけでなく、演算をも対応しているという状態のことを指します。
もう少し踏み込んだお話をすると、群\(G_1\)での演算の結果が、群\(G_2\)での演算結果と一致しているという状態と表現することも出来ます(これは誤認しがちな部分だと思いますので、後に詳しく書きます)。

「準同型写像」とは?(数学的なお話)
準同型写像
2つの群\(G_1\)、\(G_2\)の間の写像\(\phi:G_1\longrightarrow G_2\)は、群の構造を保つとき、すなわち- 任意の\(g,h\in G_1\)に対して\(\phi(gh)=\phi(g)\phi(h)\)である。
- 任意の\(g\in G_1\)に対して\(\phi(g^{-1})=\phi(g)^{-1}\)である。
- \(\phi(1_{G_1})=1_{G_2}\)である。
字面だけを見ると、「なんだ。大したこと無いじゃないか。」と思うかもしれません。
勿論、準同型写像自体は難しい概念ではありませんが、先に述べたとおり、群で重要なのは演算です。
「どの群での演算なのか?」ということに常に注意しなければなりません。
上記の準同型写像の説明は確かに正しいのですが、「どの群の演算なのか?」ということが分かりにくくもあると思います。
そこで、どの群での演算なのかを明記して少し詳しく書き直してみます。
準同型写像(演算について詳しく書いたver.)
2つの群\(G_1\)、\(G_2\)それぞれの演算を\(\ast_1\)、\(\ast_2\)とする。\(G_1\)と\(G_2\)の間の写像\(\phi:G_1\longrightarrow G_2\)は、群の構造を保つとき、すなわち- 任意の\(g,h\in G_1\)に対して\(\phi(g\ast_1h)=\phi(g)\ast_2\phi(h)\)である。
- 任意の\(g\in G_1\)に対して\(\phi(g^{-1})=\phi(g)^{-1}\)である。
- \(\phi(1_{G_1})=1_{G_2}\)である。
このように書けば、\(G_1\)の演算なのか、それとも\(G_2\)での演算なのか、ということがわかりやすいと思います。
ただ、それは上記の条件1.についてです。
条件2.および条件3.について補足説明をします。
準同型写像に対する補足説明
そもそも、準同型写像\(\phi:G_1\rightarrow G_2\)の定義域は\(G_1\)で、終域が\(G_2\)である、ということに注意しさえすれば大丈夫です。
- 条件2.について $$ (\forall g\in G_1)\ \phi(g^{-1})=\phi(g)^{-1} $$ という条件2.を言葉で書けば、
- 条件3.について これもほぼ同じです。
何が言いたいかというと、「\(\phi(g)^{-1}\)は\(G_2\)の演算\(\ast2\)における逆元ですよ。」ということです。
$$ \phi(1_{G_1})=1_{G_2} $$ という条件3.は結局の所「\(G_1\)の単位元は\(G_2\)の単位元に対応していますよ。」ということです。
準同型写像の例
例1.(部分群から群への包含写像)
\(H\)が群\(G\)の部分群だとします。
このとき、包含写像\(i:H\longrightarrow G\)、\(i(h)=h\)は準同型写像です。
実際、
- 任意の\(h_1,h_2\in H\)に対して
$$
i(h_1h_2)=h_1h_2=i(h_1)i(h_2)
$$
を満たします。 - 任意の\(h\in H\)に対して\(i(h^{-1})=h^{-1}=i(h)^{-1}\)を満たします。
- \(i(1_H)=1_H=1_G\)を満たします。
従って、\(i\)は準同型写像です。
例2.(群\(G\)から\(\mathbb{Z}\)への写像)
\(\mathbb{Z}\)は整数のたし算で群でした(これについては【代数学の基礎シリーズ】群論編 その1を御覧ください)。
\(G\)を群、\(x\in G\)とするとき、写像\(\phi:\mathbb{Z}\rightarrow G\)を\(\phi(n)=x^n\)で定めます。
このとき、
- 任意の\(m,n\in\mathbb{Z}\)に対して、
$$\phi(m+n)=x^{m+n}=x^mx^n=\phi(m)\phi(n)$$
が成り立ちます。 - 任意の\(n\in \mathbb{Z}\)に対して、
$$\phi(n^{-1})=\phi(-n)=x^{-n}=\left( x^n\right)^{-1}=\phi(n)^{-1}$$
が成り立ちます。 - \(\phi(0)=x^0=1_G\)が成り立ちます。
従って、\(\phi(n)=x^n\)で定められる写像\(\phi:\mathbb{Z}\rightarrow G\)は準同型写像です。
例3.(行列式)
\(\mathbb{R}\)は実数のかけ算で群です。
このとき、一般線形群
から\(\mathbb{R}\)への写像\(\phi:{\rm GL}_n(\mathbb{R})\rightarrow \mathbb{R}\)を、任意の\(A\in{\rm GL}_n(\mathbb{R})\)に対して\(\phi(A)=\det A\)で定めると、\(\phi\)は準同型写像です。
実際、
- \(A,B\in {\rm GL}_n(\mathbb{R})\)に対して、
$$
\phi(AB)=\det\left( AB\right)=\det A\cdot\det B=\phi(A)\phi(B)
$$
を満たします。 - 任意の\(A\in{\rm GL}_n(\mathbb{R})\)に対して、\(A\)は正則だから
$$
\phi\left( A^{-1}\right)=\det\left( A^{-1}\right)=\left( \det A\right)^{-1}=\phi(A)^{-1}
$$
を満たします。 - \(I_n\)を単位行列とするとき、
$$
\phi(I_n)=\det I_n=1
$$
を満たします。
従って、\(\phi(A)=\det A\)で定められる写像\(\phi:{\rm GL}_n(\mathbb{R})\rightarrow \mathbb{R}\)は準同型写像です。
準同型写像であることの必要十分条件
群と群の間の写像が準同型写像であることを確かめるための最も基本的な方法は、先の例のように3つの条件を確かめることです。
しかし、3つ確かめる、というのは少々面倒です(3つだけですがね)。
実は、1つ確かめるだけで準同型写像か否かを判定することが出来る、準同型写像であることの必要十分条件が存在します。
状況にも依りますが、通常は以下で示す必要十分条件を使って準同型写像か否かを判定することが多いと思います。
定理4.(準同型写像であることの必要十分条件)
\(G_1,G_2\)を群とする。写像\(\phi:G_1\rightarrow G_2\)が準同型写像であるための必要十分条件は $$ (\forall g,h\in G_1)\quad \phi\left( gh^{-1}\right)=\phi(g)\phi(h)^{-1} $$ が成り立つことである。定理4.の証明
\(G_1,G_2\)を群とするとき、写像\(\phi:G_1\rightarrow G_2\)が準同型写像だとすると、任意の\(g,h\in G_1\)に対して
$$
\phi\left( gh^{-1}\right)=\phi(g)\phi\left( h^{-1}\right)=\phi(g)\phi(h)^{-1}
$$
が成り立ちます。
逆に、写像\(\phi:G_1\rightarrow G_2\)が、任意の\(g,h\in G_1\)に対して
$$
\phi\left( gh^{-1}\right)=\phi(g)\phi(h)^{-1}
$$
を満たしているとします。
まず、
$$
\phi(1_{G_1})=\phi(1_{G_1}1_{G_1}^{-1})=\phi(1_{G_1})\phi(1_{G_1})^{-1}=1_{G_2}
$$
だから、準同型写像の条件3.が成り立ちます。
次に、任意の\(h\in G_1\)に対して
$$
1_{G_2}=\phi(1_{G_1})=\phi\left( hh^{-1}\right)=\phi(h)\phi\left( h^{-1}\right)
$$
であるので、\(\phi\left( h^{-1}\right)=\phi(h)^{-1}\)だから、準同型写像の条件2.が成り立ちます。
最後に、任意の\(g,h\in G_1\)に対して
\begin{eqnarray}
\phi\left( gh\right)&=&\phi\left( g(h^{-1})^{-1}\right)\\
&=&\phi(g)\phi\left( h^{-1}\right)^{-1}\\
&=&\phi(g)\left( \phi(h)^{-1}\right)^{-1}\\
&=&\phi(g)\phi(h)
\end{eqnarray}
が成り立つので、準同型写像の条件1.が成り立ちます。
従って、\(\phi\)は準同型写像です。
定理4.の証明終わり
核(kernel)
次に核という概念を解説します。
(字面だけを見ると少々怖いですが、数学の範囲では何も怖くありません)
核(kernel)を一言で。
核を一言で述べれば
です。
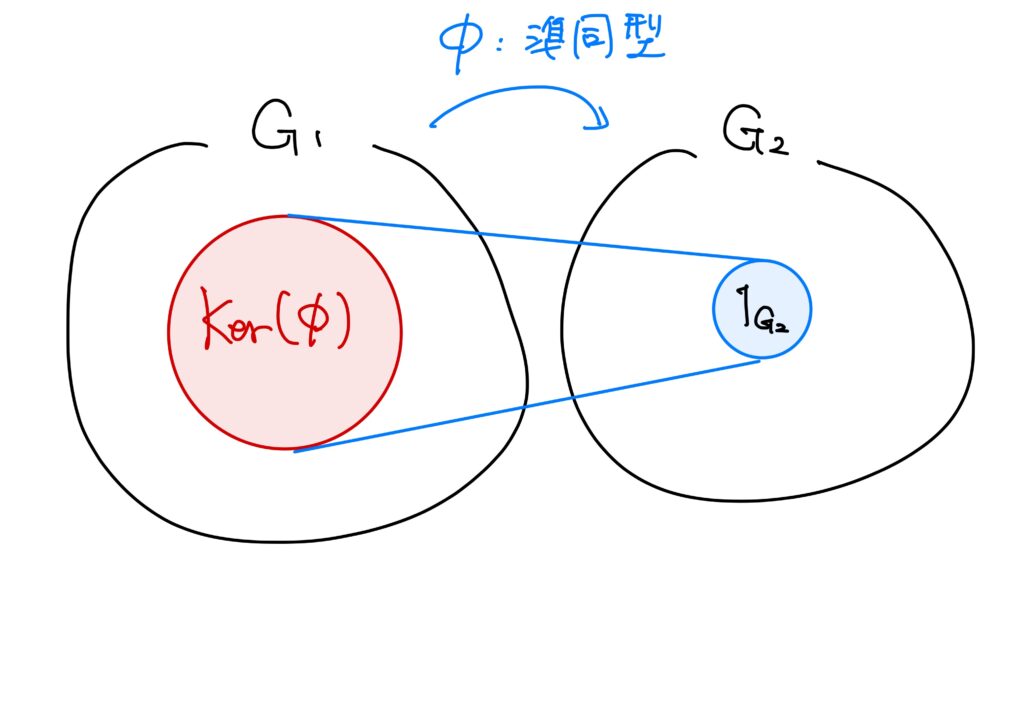
実は、この核は、準同型写像での対応先の群の正規部分群となっています(後で証明します)。
「核」とは?(数学的なお話)
核(kernel)
\(G_1\)、\(G_2\)を群、\(\phi:G_1\longrightarrow G_2\)を準同型写像とする。このとき $$ {\rm Ker}(\phi)=\left\{x\in G_1\middle|\phi(x)=1_{G_2}\right\} $$ を準同型写像\(\phi\)の核(kernel)という。\({\rm Ker}(\phi)\)は定義域の部分集合、すなわち準同型写像\(\phi:G_1\longrightarrow G_2\)に対して\({\rm Ker}(\phi)\subset G_1\)であることに注意です。
「核」の例
(今思うと字面が怖いですねえ…)
例2.の\({\rm Ker}(\phi)\)
\(G\)を群、\(x\in G\)とするとき、写像\(\phi:\mathbb{Z}\rightarrow G\)を\(\phi(n)=x^n\)で定めると、\(\phi\)は準同型写像でした。
このときの\({\rm Ker}(\phi)\)は
$$
{\rm Ker}(\phi)=\left\{n\in\mathbb{Z}\middle|x^n=1_G\right\}
$$
です。
例3.の\({\rm Ker}(\phi)\)
\(\mathbb{R}\)は実数のかけ算で群でした。
このとき、一般線形群
から\(\mathbb{R}\)への写像\(\phi:{\rm GL}_n(\mathbb{R})\rightarrow \mathbb{R}\)を、任意の\(A\in{\rm GL}_n(\mathbb{R})\)に対して\(\phi(A)=\det A\)で定めると、\(\phi\)は準同型写像でした。
このときの\({\rm Ker}(\phi)\)は
\begin{eqnarray}
{\rm Ker}(\phi)&=&\left\{A\in{\rm GL}_n(\mathbb{R})\middle|\phi\left(A \right)=1\right\}\\
&=&\left\{A\in{\rm GL}_n(\mathbb{R})\middle|\det A=1\right\}\\
&=&{\rm SL}_n(\mathbb{R})
\end{eqnarray}
です。
なんと、\({\rm GL}_n(\mathbb{R})\)における行列式を、行列を実数に対応させる写像だと捉えると、行列式は準同型写像であり、なおかつ行列式の核は\({\rm SL}_n(\mathbb{R})\)だと言うことです。
核\({\rm Ker}(\phi)\)は正規部分群です。
定理5.
\(G_1\)、\(G_2\)を群、\(\phi:G_1\longrightarrow G_2\)を準同型写像とする。このとき、\({\rm Ker}(\phi)\triangleleft G_1\)、すなわち\(\phi\)の核\({\rm Ker}(\phi)\)は\(G_1\)の正規部分群である。定理5.の証明
$$
{\rm Ker}(\phi)=\left\{x\in G_1\middle|\phi(x)=1_{G_2}\right\}
$$
でした。
まずは、\({\rm Ker}(\phi)\)が\(G_1\)の部分群であることを、以下の定理を使って確かめます。
定理6.(部分群であることの必要十分条件)
群\(G\)の部分集合\(H\)が\(G\)の部分群になるための必要十分条件は次の3つの条件が満たされることである。- \(1_G\in H\)である。ただし、\(1_G\)は群\(G\)の単位元である。
- \(x,y\in H\Rightarrow xy\in H\)である。
- \(x\in H\Rightarrow x^{-1}\in H\)である。
定理6.の証明は【代数学の基礎シリーズ】群論編 その2を御覧ください。
- \(1_{G_1}\in {\rm Ker}(\phi)\)です。
- 任意の\(x,y\in{\rm Ker}(\phi)\)に対して、\(\phi\)は準同型写像だから、
$$
\phi(xy)=\phi(x)\phi(y)=1_{G_1}1_{G_1}=1_{G_1}
$$
となるため、\(xy\in{\rm Ker}(\phi)\)です。 - \(x\in{\rm Ker}(\phi)\)とすると、
$$
\phi\left( x^{-1}\right)=\phi(x)^{-1}=1_{G_1}^{-1}=1_{G_1}
$$
となるため、\(x^{-1}\in {\rm Ker}(\phi)\)です。
従って、定理6.から\({\rm Ker}(\phi)\)は\(G_1\)の部分群です。
次に、\({\rm Ker}(\phi)\)が\(G_1\)の正規部分群であることを示します。
任意の\(h\in{\rm Ker}(\phi)\)に対して、\(\phi(h)=1_{G_1}\)だから、任意の\(g\in G_1\)に対して
\begin{eqnarray}
\phi\left( ghg^{-1}\right)&=&\phi(g)\phi(h)\phi\left(g^{-1} \right)\\
&=&\phi(g)\phi(h)\phi(g)^{-1}\\
&=&\phi(g)1_{G_1}\phi(g)^{-1}\\
&=&\phi(g)\phi(g)^{-1}\\
&=&1_{G_1}
\end{eqnarray}
であるので、\(ghg^{-1}\in{\rm Ker}(\phi)\)です。
従って、\({\rm Ker}(\phi)\)は\(G_1\)の正規部分群です。
定理5.の証明終わり
準同型写像が単射であることの必要十分条件
定理7.
準同型写像\(\phi:G_1\longrightarrow G_2\)が単射であるための必要十分条件は、\({\rm Ker}(\phi)=\left\{1_{G_1}\right\}\)となることである。定理7.の証明
\(\phi:G_1\longrightarrow G_2\)が単射であれば、\(\phi(g)=1_{G_2}\)を満たすような\(g\in G_1\)に対して、\(\phi(g)=\phi(1_{G_1})\)だから、\(g=1_{G_1}\)です。
つまり、\({\rm Ker}(\phi)=\left\{1_{G_1}\right\}\)です。
逆に、\({\rm Ker}(\phi)=\left\{1_{G_1}\right\}\)ならば、\(\phi(g_1)=\phi(g_2)\)のとき、
$$
\phi\left(g_1g_2^{-1} \right)=\phi(g_1)\phi(g_2)^{-1}=1_{G_2}
$$
だから、\(g_1g_2^{-1}=1_{G_1}\)です。
従って、\(g_1=g_2\)となって、\(\phi\)は単射です。
定理7.の証明終わり
同型写像と同型
最後に、同型写像と同型について解説します。
同型写像
簡単です。
同型写像を一言で述べれば、
です。
つまり、群の演算を保ち、しかも各群の要素が1つ1つ対応しているような写像が同型写像です。
同型写像
全単射であるような準同型写像、すなわち、準同型写像\(\phi:G_1\longrightarrow G_2\)が\({\rm Ker}(\phi)=\left\{1_{G_1}\right\}\)かつ\({\rm Image}(\phi)=G_2\)を満たすとき、同型写像(isomorphism)と呼ぶ。先にも述べましたが、要するに全単射準同型が同型写像です。
同型
群における同型というのは
ということです。
これを数学的に書けば、以下です。
同型
群\(G_1\)、\(G_2\)の間に同型写像が存在するとき、それらは同型(isomorphic)と呼ばれ、このとき\(G_1\cong G_2\)と書く。先に、同型写像は
と述べました。
読んで字の如しなのですが、「要素同士だけでなく、群の演算も保つような全単射な写像」が同型写像なので、同型写像が存在するような群同士は”同”じ”型”をしているというわけです。
要するに、群の構造を保ち、かつ要素同士も一対一対応しているということから、同型な群同士は本質的に同じものとして扱うことが出来ます。
少し踏み込んだ話をすると、同型な群同士は「ピッタリと一致するわけではないけれど、同じものとして扱って良い。」というわけです。
扱いにくいような群(複雑な集合)に同型なシンプルな群を見つけ、複雑な群に対応させたシンプルな群で考察し、その後逆写像でもとに戻して結論を得る、みたいなことができるというわけです。
自己同型群
群\(G\)から\(G\)自身への同型写像を自己同型写像といいいます。
「そんなの恒等写像だけじゃない?」と思われるかもしれませんが、それだけではありません。
例えば、\(\mathbb{Z}\)は整数のたし算で群となるのでした。
このとき、写像\(\varphi:\mathbb{Z}\longrightarrow \mathbb{Z}\)を、任意の\(n\in\mathbb{Z}\)に対して\(\varphi(n)=-n\)で定めても、この\(\varphi\)は全単射かつ準同型なので、同型写像です。
今紹介したのは誠に簡単な例ではありますが、自己同型写像は恒等写像だけでなく他にも定め方によってはたくさんあります。
そこで、\(G\)の自己同型写像、すなわち\(G\)から\(G\)自身への同型写像の集合を\({\rm Aut}(G)\)と書くことにします。
自己同型
群\(G\)から\(G\)自身への同型写像を\(G\)の自己同型写像(automorphism)といい、\(G\)の自己同型写像全体の集合を\({\rm Aut}(G)\)と書く。すなわちこの群\(G\)の自己同型写像全体の集合\({\rm Aut}(G)\)に演算を定めます。
任意の\(\phi,\psi\in{\rm Aut}(G)\)に対して、\({\rm Aut}(G)\)の演算を写像の合成\(\phi\circ\psi\)で定めます。
すると、
- 結合律
任意の\(\phi,\psi,\omega\in{\rm Aut}(G)\)、任意の\(g\in G\)に対して
\begin{eqnarray}
\left(\left(\phi\circ \psi \right)\circ \omega\right)(g)&=&\left(\phi\circ \psi \right)\left(\omega(g)\right)\\
&=&\phi\left(\psi\left(\omega(g)\right)\right)\\
&=&\phi\left(\left(\psi\circ\omega\right)(g)\right)\\
&=&\left(\phi\circ\left(\psi\circ\omega\right)\right)(g)\\
\end{eqnarray}
となるので結合律が成り立ちます。 - 単位元の存在
恒等写像\({\rm id}_{G}\)は\({\rm Aut}(G)\)の単位元です。
実際、任意の\(\varphi\in{\rm Aut}(G)\)、任意の\(g\in G\)に対して
\begin{eqnarray}
\left( \varphi\circ {\rm id}_G\right)(g)=\varphi(g),\\
\left( {\rm id}_G\circ \varphi\right)(g)=\varphi(g)
\end{eqnarray}
となるからです。 - 逆元の存在
任意の\(\varphi\in{\rm Aut}(G)\)は全単射なので、逆写像\(\varphi^{-1}:G\longrightarrow G\)が存在します。
任意の\(g\in G\)に対して、
\begin{eqnarray}
\left( \varphi\circ \varphi^{-1}\right)(g)={\rm id}_G(g)=g,
\left( \varphi^{-1}\circ \varphi\right)(g)={\rm id}_G(g)=g
\end{eqnarray}
が成り立つので、\({\rm Aut}(G)\)の任意の要素\(\varphi\)に逆元が存在します。
故に、\({\rm Aut}(G)\)は写像の合成という演算で群となります。
この\({\rm Aut}(G)\)を自己同型群といいます。
自己同型群
群\(G\)の自己同型写像全体の集合\({\rm Aut}(G)\)は、写像の合成を演算として群となる。この\({\rm Aut}(G)\)を自己同型群という。ここで、自己同型群の性質を一つ紹介します。
定理8.
\(G\)を群、\(g\in G\)とするとき、写像\(i_g:G\longrightarrow G\)を、任意の\(h\in G\)に対して\(i_g(h)=ghg^{-1}\)で定める。また、写像\(\varphi:G\longrightarrow {\rm Aut}(G)\)を、任意の\(g\in G\)に対して\(\varphi(g)=i_g\)で定める。このとき、\(\varphi\)は準同型写像である。定理8.の証明
\(g_1,g_2\in G\)とします。
\(h\in G\)に対して、
\begin{eqnarray}
\varphi(g_1g_2)(h)&=&i_{g_1g_2}(h)\\
&=&g_1g_2h(g_1g_2)^{-1}\\
&=&g_1g_2hg_2^{-1}g_1^{-1}\\
&=&i_{g_1}\left( i_{g_2}(h)\right)\\
&=&\left(\varphi(g_1)\circ \varphi(g_2)\right)(h)\\
&=&\varphi(g_1)\varphi(g_2)(h)
\end{eqnarray}
となります。
従って、\(\varphi(g_1g_2)=\varphi(g_1)\varphi(g_2)\)であるため、\(\varphi\)は準同型写像です。
定理8.の証明終わり
皆様のコメントを下さい!
今回はフェルマーです。
ピエール・ド・フェルマー(1601-1655)はフランスの数学者。
本職は弁護士であり、南フランスの町トゥルー ズの高等行政官の地位(正確には王立議会の議員の職)につきましたが、余暇はすべて数学の研究に費やしたといわれています。
\(x^n+y^n=z^nが\(n\geq3\)の場合は自然数解を持たないというフェルマー予想(フェルマーの大定理)で有名です。
ディオファントスの「数論」(バシュが翻訳した1637年度版)の自筆写本の余白に、「(フェルマーの大定理の)証明を書くには、場所が十分ではない」と書き込んだと言われています(完全な証明は、1994年にワイルズにより与えられました)。
この他にも、数論(不定方程式論)についての様々な結果を友人(メルセンヌ、パスカル、カルカヴィ)への書簡の中で言明し、後の時代に大きな影響を与えました(オイラーもその一人です)。
確率論、微分積分学でも先駆的な業績を残しています。
最小作用の原理に繋がるアイディアを用いて屈折の法則を説明したことも顕著な業績です。
如何でしたか?
フェルマーの大定理は「フェルマーの最終定理」という名前でも有名ですよね。
ここに書かれている事のほかにでフェルマーについてご存知のことがあれば是非コメントで教えて下さい!
結
今回は準同型写像、核(kernel)、同型について解説しました。
準同型写像とは、群の構造を保つような群同士の間の写像、核は準同型写像でもって終域の単位元に写される定義域の要素の集合、同型は準同型写像が全単射であるときをいいます。
次回は商群(剰余群)について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
代数についてより詳しく知りたい方は以下を参考にすると良いと思います!





コメントをする
定理8にてφ^-1が準同型写像となっていますが、φの誤りかと思われます。
名無し様
ご指摘ありがとうございます。
訂正いたしました。
同型写像の定義で Image(φ) = G1 となっていますが、G2の誤りかと思われます。
名無し様
ご指摘ありがとうございます。
おっしゃるとおり、誤りでした。
訂正致しました。