「軌道、推移的な作用、等質空間、安定化群とは？」【代数学の基礎シリーズ】群論編その14

代数学

2023.03.04 2022.11.03

本記事の内容
軌道
1. まずは例から。
2. 軌道を数学的に書くと以下です。
推移的な作用、等質空間
安定化群
例
1. 例1.
2. 例2.
諸性質
皆様のコメントを下さい！
結

本記事の内容

本記事は、軌道、推移的な作用、等質空間、安定化群について解説する記事です。

本記事を読むに当たり、群作用について知っている必要があるため、以下の記事も合わせてご覧ください。

軌道

まずは、例から考えてみます。

まずは例から。

$G={\rm SO}(2)=\left\{ R_\theta= \begin{pmatrix} \cos\theta&-\sin\theta\\ \sin\theta&\cos\theta \end{pmatrix} \middle| \theta\in\mathbb{R}\right\},\quad X=\mathbb{R}^2$
とします。
このとき、 $G$ は行列の積で $X$ に左から作用しています。
$\mathbb{R}^2$ の要素は $\displaystyle\left(\begin{array}{c}x\\y\end{array}\right)$ と書きます。

$a(>0)\in\mathbb{R}$ に対して、
$\left(\begin{array}{c}a\\0\end{array}\right)= \left(\begin{array}{c}a\cos\theta\\ a\sin\theta\end{array}\right)$
です。

ここで、 $\boldsymbol{x}\in X=\mathbb{R}^2$ に対して集合
$G\boldsymbol{x}=\left\{g\boldsymbol{x}\middle|g\in G\right\}$
という集合を考えます。
このとき、
$\begin{eqnarray} G\boldsymbol{x}&=&{\rm SO}(2)\boldsymbol{x}\\ &=&\left\{g\boldsymbol{x}\middle|g\in {\rm SO}(2)\right\}\\ &=&\left\{\begin{pmatrix} \cos\theta&-\sin\theta\\ \sin\theta&\cos\theta \end{pmatrix} \left(\begin{array}{c}x\\ y\end{array}\right) \middle|\theta\in\mathbb{R}\right\}\\ &=&\left\{\left(\begin{array}{c}x\cos\theta-y\sin\theta\\ x\sin\theta+y\cos\theta\end{array}\right) \middle|\theta\in\mathbb{R}\right\}\\ \end{eqnarray}$
です。

故に、点 $\displaystyle\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}a\\0\end{array}\right)$ は半径 $a$ の円上を動きます。

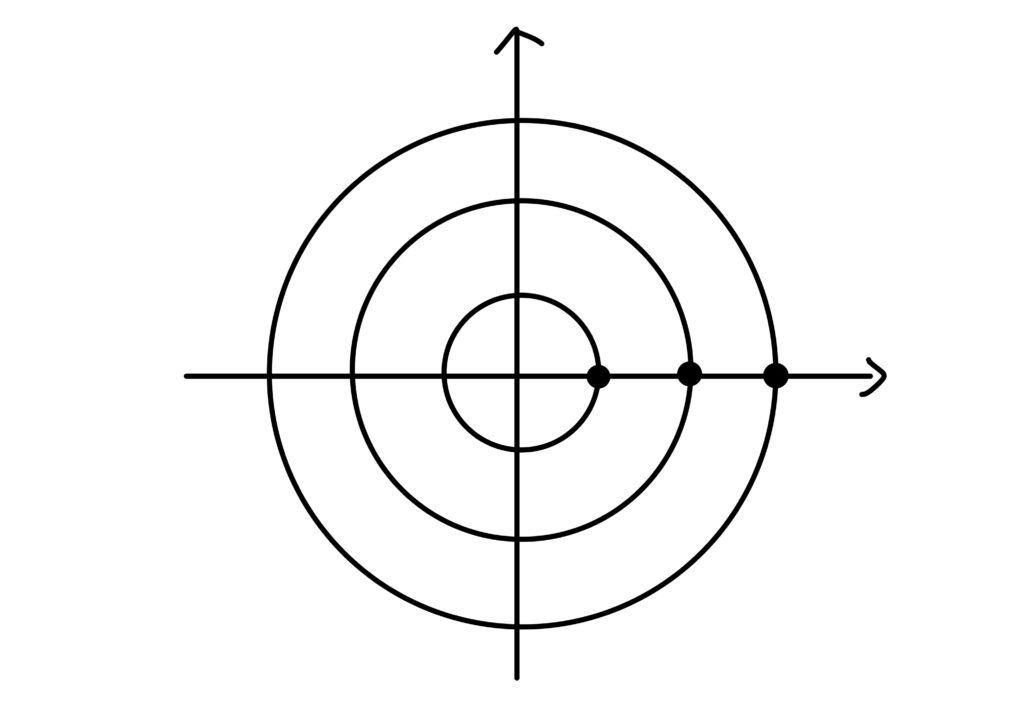
この集合
$G\boldsymbol{x}=\left\{g\boldsymbol{x}\middle|g\in G\right\}$
を $\boldsymbol{x}$ の $G$ による軌道といいます。

軌道を数学的に書くと以下です。

軌道

群

$G$ が集合

$X$ に左から作用するとする。

$x\in X$ のとき

$Gx=\left\{gx\middle| g\in G\right\}$ と書き、

$x$ の

$G$ による軌道という。

言い換えれば、軌道というのは $G$ の要素で移り合うような $X$ の要素全体の集合です。

推移的な作用、等質空間

これらについては早速ながら、数学的に説明していまいます。

推移的な作用と等質空間の数学的な説明

推移的な作用、等質空間

群

$G$ が集合

$X$ に左から作用するとする。

$x\in X$ が存在して、

$Gx=X$ となるとき、この作用は推移的であるという。また、

$X$ は

$G$ の等質空間という。

つまりどういうことですか？(推移的な作用)

推移的な作用を論理式で書くと
$(\forall p,\ q\in X)\ (\exists g\in G)\ {\rm s.t.}\ gp=q$
ということです。
つまり、推移的な作用を粗く言えば

群の作用によって、

$X$ のどこから

$X$ のどこへでも移れる。

ということです。

つまりどういうことですか？(等質空間)

また、等質というのは、粗く言えば

等質とは、どの点の周りでも性質が等しい。

ということです。
例えば、円 $S^1=\left\{(x,y)\in\mathbb{R}^2\middle| x^2+y^2=1\right\}$ はどの点の周りでも性質が同じです。
というのも、任意の $\boldsymbol{x},\boldsymbol{y}\in S^1$ に対して、回転させることで $\boldsymbol{x}$ を $\boldsymbol{y}$ に移すことができるからです。

群作用の言葉を使えば、 ${\rm SO}(2)$ が $S^1$ に推移的に作用している、ということです。

まとめると…

要するに、まとめれば、群が集合に推移的に作用していると、どの点の周りでも性質が等しいので、軌道空間が特別な集合になる、ということになります。
つまり、もとの集合 $X$ を考える代わりに、軌道空間で考えることができる、というわけです。
軌道空間で考えることで、群の性質だったりを使うことができるため、扱う武器が増える、ということになります。

安定化群

軌道を言い換えれば、「 $G$ の要素で移り合う $X$ の要素全体の集合」でした。
1つの軌道に含まれる要素の個数を軌道の長さと言ったりします。
軌道 $Gx$ において、 $g\in G$ は $G$ 全体を動くので、 $Gx$ は直感的には $G$ の要素の同じ数の要素を持ちます。
しかしながら、この中には同じものも含まれていて、実際には $G$ の要素の数よりも少ないこともあります。
そこで、 $g,h\in G$ に対して、いつ $gx=hx$ が成り立つのか？ということを考えます。
$gx=hx$ とすると、
$x=1_Gx=\left( g^{-1}g\right)x=g^{-1}(gx)=g^{-1}(hx)=\left( g^{-1}h\right)x$
です。
そこで、
$G_x=\left\{g\in G\middle| gx=x\right\}$
として、これを $x$ の $G$ における安定化群といいます。
実は、安定化群は $G$ の部分群になります。
それ故、安定化群は安定化部分群と呼ばれたりもします。

安定化群

群

$G$ が集合

$X$ に左から作用するとする。

$x\in X$ のとき、

$G_x=\left\{g\in G\middle|gx=x\right\}$ を $x$ の( $G$ における)安定化群という。

例

例1.

群 $G$ の $G$ 自身への左からの席による作用を考えます。
つまり、 $X=G$ とし、 $g\in G$ 、 $x\in X=G$ に対して、 $gx\in G=X$ を $g$ の要素としての演算とします。
すなわち $\psi:G\times X=G\times G\ni (g,x)\mapsto \psi(g,x)\in X=G$ を $\psi(g,x)=gx$ と定めた、ということです。
故に、

$\psi(1_G,x)=1_Gx=x$ 、
$\psi\left(g,\psi(h,x)\right)=\psi(g,hx)=ghx=(gh)x=\psi(hg,x)$

となるため、 $\psi$ は $G$ の $X=G$ への左作用です。
右からの演算を考えると、 $G$ から $G$ への右作用を得ます。

$g\in G$ ならば、 $g=g1_G$ ですので、 $g\in G1_G$ です。
故に、 $G=G1_G$ ですのでこの作用は推移的です。
$g1_G=1_G$ であれば、 $g=1_G$ ですので、 $1_G$ の安定化群は自明な群、すなわち $\left\{1_G\right\}$ です。

例2.

$G=\mathcal{G}_n$ の $X=\left\{1,\dots,n\right\}$ への作用を考えます。
ただし、 $\mathcal{G}_n$ は対称群と呼ばれる群でした(詳しくは【代数学の基礎シリーズ】群論編その1を御覧ください)。

$\sigma=(i\ n)$ であれば、 $\sigma(n)=i$ なので、この作用は推移的です。
$n$ の安定化群は $H=\left\{\sigma\in \mathcal{G}_n\middle|\sigma(n)=n\right\}$ です。
$\sigma\in H$ は $n$ を普遍にするので、 $Y=\left\{1,\dots, n-1\right\}$ の置換を引き起こします。
故に、安定化群 $G_n$ を $\mathcal{G}_{n-1}$ とみなすことが出来ます。
従って、 $\mathcal{G}_n/{\mathcal{G}_{n-1}}$ は $\left\{1,\dots,n\right\}$ と一対一対応します。

諸性質

命題1.

$G$ が

$X$ に作用し、

$x,y\in X$ 、

$g\in G$ で

$gx=y$ なら、

$Gy=Gx$ 、

$G_y=gG_xg^{-1}$ である。

命題1.の証明

$h\in G$ なら $hy=hgx\in Gx$ なので、 $Gy\subset Gx$ です。
$x=g^{-1}y$ なので、 $Gx\subset Gy$ とものあり、 $Gx=Gy$ です。
$h\in G$ であれば、
$\begin{eqnarray} h\in G_y&\Longleftrightarrow&hy=y\\ &\Longleftrightarrow&hgx=gx\\ &\Longleftrightarrow&g^{-1}hgx=x\\ &\Longleftrightarrow&g^{-1}hg\in G\\ &\Longleftrightarrow&h\in gG_xg^{-1} \end{eqnarray}$
です。
従って、 $G_y=gG_xg^{-1}$ です。

命題1.の証明終わり

系2.

$G$ が集合

$X$ に作用し、

$x,y\in X$ で

$Gx\cap Gy\neq\emptyset$ なら、

$Gy=Gx$ 、

$G_y\cong G_x$ である。

系2.の証明

$z\in Gx\cap Gy$ なら、 $z=g_1x=g_2y$ となるような $g_1,g_2\in G$ が存在します。
$y=g_2^{-1}g_1x$ となるので、命題1.から $Gx=Gy$ です。
$g=g_2^{-1}g_1$ とおくと、 $G_y=gG_xg^{-1}$ ですが、 $\varphi:G_x\ni h\mapsto ghg^{-1}\in G_y$ とすると、 $h_1,h_2\in G_x$ に対して
$\varphi\left( h_1h_2\right)=gh_1h_2g^{-1}=gh_1h_2g^{-1}=hg_1g^{-1}gh_2g^{-1}=\varphi(h_1)\varphi(h_2)$
により $\varphi$ は準同型です。
$h\mapsto g^{-1}hg$ が $\varphi$ の逆写像なので、 $\varphi$ は同型写像です。

系2.の証明終わり

系3.

群

$G$ が集合

$X$ に作用するとき、

$x,y\in X$ で

$Gx=Gy$ のときに

$x\sim y$ として関係を定める。このときの関係

$\sim$ は

$X$ 上の同値関係である。また、この同値関係による剰余類は

$X$ 上の軌道と一対一対応する。

系3.の証明

まずは関係 $\sim$ が同値関係になることを示しますが、証明するまでもないような感じです。
$Gx=Gx$ なので $x\sim x$ です。
$Gx=Gy$ なら $Gy=Gx$ なので $x\sim y$ なら $y\sim x$ です。
$Gx=Gy$ 、 $Gy=Gz$ なら $Gx=Gz$ なので $x\sim y$ 、 $y\sim z$ なら $x\sim z$ です。
故に $\sim$ は同値関係です。

命題1.により、 $y\sim x$ は $y\in Gx$ と同値です。
故に、 $x$ の同値類は $Gx$ と一致します。

系3.の証明終わり

同じ軌道に属することが同値関係なので、 $y\in Gx$ であるとき、 $y$ はこの軌道の代表元であるといいます。
また、各軌道の代表元をちょうど一つずつ含む部分集合を軌道の完全代表系といいます。

皆様のコメントを下さい！

今回はブルバキです。

ニコラ・ブルバキ(Bourbaki)は、1934年にフランスにおいて「数学原論」という著作を刊行するための共同作業に加わった数学者集団のペンネームです。
1939年に最初の巻が出版されて以来、集合論、代数学、実1変数関数論、位相線形空間、積分、リー群とリー環、可換環、スペクトル理論、可微分多様体、解析多様体についての巻が継続的に出版されましたが、現在は「数学原論」の出版については一応終止符を打っています。
しかし、ブルバキセミナーの名のもとに、現在でも最先端の数学について質の高い報告が行われており、セミナーノートの出版が続いています。
初期のブルバキのメンバーは、アンリ・カルタン、クロード・シュヴァレー、ジャン・デルサルト、ジャン・デュドネ、スツオレム・マンデルブロー、ルネ・ド・ボッセル、アンドレ・ヴェイユです。
ブルバキの活動の背景には、ヒルベルトの影響化でドイツにおける数学研究(特に代数学、解析学)が現代化しつつあったことに比べて、フランスが概して古典的な数学に留まっていたことに対する若い世代の不満があったといわれます。
従って，フランスの大学における数学教育の改革が所期の目標でした。
また、数学の諸理論を、1つの「原理」のもとに纏めようという機運は、当時の数学の発展の状況下では自然なことでした。
ブルバキ自身による構造主義に対する考え方は、「数学的建築術」(1948年)という短い著作の中に表明されています。

如何でしたか？
ペンネームで有名な数学者集団もいるのですね。
ここに書かれれいることの他にブルバキについてご存知のことがあれば、ぜひコメントで教えて下さい！

結

今回は、軌道、推移的な作用、等質空間、安定化群について解説しました。
それぞれ

軌道：群の要素で移り合うような集合の要素全体。
推移的な作用：群の作用によって、集合のどこからどこへでも移れるような作用。
等質：どの点の周りでも性質が等しい。
安定化群：作用しても不変な群の要素の集合。

です。

次回は推移的な作用と有限群の要素の個数に関する事実を解説します。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよよ一週間以内にお答えします。

代数についてより詳しく知りたい方は以下を参考にすると良いと思います！

コメントをする

名前:名無しさん : 投稿日：2023/02/16(木) 17:29:31 ID：MzODMzOTM

系3の証明終わり、以降に誤字がたくさんあります。

返信

名前:オノコウスケ : 投稿日：2023/02/19(日) 03:09:41 ID：Y1MDQ3MDI

名無し様

ご指摘ありがとうございます。
訂正いたしました。

返信

名前:naru : 投稿日：2023/02/23(木) 14:35:48 ID：E0ODA5OTA

　「プリンストン数学大全」より、軌道、推移的作用などについてモチベーションをわからせようにと書かれています。曰く、「GのXへの作用は、一つの軌道しか持たないとき推移的であるという。言い換えれば、…。作用が推移的でないときは、それぞれの軌道への作用を別々に考えることができ、元の作用を共通部分のない軌道それぞれへの作用に事実上分けることができる。そこで、Gの集合への作用をすべて調べるには、推移的作用のみを調べればよい」（p.469,「作用」の項）
　読み取りにくいのです。推移的作用の定義があり、推移的でない場合は、と続く。「作用をすべて調べるには、推移的作用のみを調べればよい」。推移的作用のみ？推移的でない場合は、どうすればいいのか、わかりにくいです。ご教示ください。

返信

名前:オノコウスケ : 投稿日：2023/03/04(土) 23:11:30 ID：I2NTQ2OTg

naru様

返信が遅れてしまい申し訳ありません。
私はプリンストン数学大全を持ち合わせておりませんので、厳密な解答とはならないかもしれませんが、その点ご了承下さい。

>「作用をすべて調べるには、推移的作用のみを調べればよい」。推移的作用のみ？推移的でない場合は、どうすればいいのか、わかりにくいです。ご教示ください。
というお問い合わせですが、推移的でない場合は、naru様のコメントにあるように「作用が推移的でないときは、それぞれの軌道への作用を別々に考えることができ、元の作用を共通部分のない軌道それぞれへの作用に事実上分けることができる。」ということになります。
この文章を平たく言い換えれば、「推移的でない作用は、推移的な作用の”集まり”としてある種”分解”することができるため、結局は”分解した”個々の推移的な作用を考えれば良い」ということだと思います。
なぜそのようにできるのか？ということの触りをここで解説致します。

$G$ を群、 $X$ を集合、 $\varphi:G\times X\longrightarrow X$ を $G$ の $X$ への左作用とします(右作用も同じように考えることができます)。
このとき、 $X$ に関係 $\sim$ を以下で定めます。
$(\forall x,y\in X)\quad x\sim y\Longleftrightarrow (\exists g\in G)\ {\rm s.t.}\ y=gx\left( =\varphi(g,x)\right)$
この関係 $\sim$ は同値関係です(簡単に確かめられます)。
このとき $x\in X$ の同値類 $C(x)$ は
$\begin{eqnarray} C(x)&=&\left\{y\in X\middle| y\sim x\right\}\\ &=&\left\{y\in X\middle|(\exists g)\ {\rm s.t.}\ y=gx\right\}\\ &=&\left\{gx\middle| g\in G\right\}\\ &=&Gx \end{eqnarray}$
となります。
ただし、 $Gx$ は $x\in X$ の $G$ による軌道(空間)です。
すなわち、先程定めた関係 $\sim$ は同値関係であり、その同値類は軌道(空間)と一致するわけです。
さて、 $\forall a,b\in Gx$ に対して、 $Gx$ は同値関係 $\sim$ の同値類ですから、 $a\sim b$ です。
すなわち、
$(\exists g^\prime\in G)\ {\rm s.t.}\ a=g^\prime b\left( =\varphi(g^\prime,b)\right)\tag{$\ast$}$
が成り立っています。
ここで、推移的な作用とは何だったかというと、

推移的な作用(言い換え。記事内に有り)

群 $G$ が集合 $X$ に左から作用するとする。このとき作用 $\varphi:G\times X\longrightarrow X$ が
$(\forall p,q)(\exists g\in G)\ {\rm s.t.}\ q=\varphi(g,p)$
を満たすならば、 $\varphi$ は推移的、または作用 $\varphi$ は推移的な作用という。

でした。
故に、今考えている作用 $\varphi$ は推移的であるということになります。
したがって、平たく言えば、各軌道では作用が推移的になっており、各軌道は同値類であるから、 $X$ をクラス分け(共通部分が存在しない集合の和集合)しています。
そういう意味で、結局の所は各軌道では作用が推移的だから、各軌道で推移的な作用を考える、ということを繰り返せばよいのだ、ということになります。
恐らく、プリンストン数学大全で述べているのはそういうことだと思われます。

返信

名前:名無しさん : 投稿日：2023/07/22(土) 18:19:42 ID：ExNDY1OTQ

軌道をもっと例を挙げて
具体的に説明して頂きたい

返信

名前:オノコウスケ : 投稿日：2023/07/23(日) 22:50:28 ID：gxNjQ4NDM

名無し様

>軌道をもっと例を挙げて具体的に説明して頂きたい
とのお問い合わせですが、お答えします。

例1.
本記事で挙げた例とほぼ同じですが、 ${\rm SO}(3)$ の $\mathbb{R}^3$ への作用による軌道空間は同心球面です。

例2.(これは作用の例も含まれますが)
$n$ を正の整数とし、 $S$ を集合とします。
$S^n$ を $S$ の $n$ 個の直積集合、すなわち
$S^n:=S\times\cdots\times S=\left\{ (s_1,\dots,s_n)\mid s_i\in S,\ i=1,\dots,n\right\}$
とします。
このとき、写像 $\varphi:\mathcal{S}_n\times S^n\longrightarrow S^m$ を
$\left(\sigma,(s_1,\dots,s_n) \right)\mapsto \sigma\cdot(s_1,\dots,s_n):=\left( s_{\sigma^{-1}(1)},\dots,s_{\sigma^{-1}(n)}\right)$
で定めます。
ただし、 $\mathcal{S}_n$ は $n$ 次対称群です。
この写像 $\varphi$ は、 $S^n$ 穰の $\mathcal{S}_n$ の作用です。
ちなみに
「どうして $\sigma^{-1}$ ？」と思われたかもしれませんが、 $\sigma$ の作用が $s_k$ を $\sigma(k)$ に移動させる、と考えればOKです。

例えば、 $n=6$ 、 $S=\left\{ {\rm C},\ {\rm E},\ {\rm F},\ {\rm O}\right\}$ とすると、
$\begin{eqnarray} &&\begin{pmatrix} 1&2&3&4&5&6\\ 2&6&3&5&4&1 \end{pmatrix}\cdot \left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left({\rm E},\ {\rm C},\ {\rm F},\ {\rm E},\ {\rm F},\ {\rm O} \right)\\ &&\begin{pmatrix} 1&2&3&4&5&6\\ 1&3&2&4&5&6 \end{pmatrix}\cdot \left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left({\rm C},\ {\rm F},\ {\rm O},\ {\rm F},\ {\rm E},\ {\rm E} \right)\\ &&\begin{pmatrix} 1&2&3&4&5&6\\ 1&2&4&3&6&5 \end{pmatrix}\cdot \left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right) \end{eqnarray}$
ということです。
とどのつまり、 $n$ 次対称群 $\mathcal{S}_n$ を長さ $n$ の $S$ の要素からなる文字列の置換として作用させているということです。
$n$ 次二面体群 $D_n$ は、 $n\geq 3$ のとき $D_n\subset\mathcal{S}_n$ です(二面体群については【代数学の基礎シリーズ】群論編その12を御覧ください)。
故に、 $\mathcal{S}_n$ の $S^n$ への作用は、 $D_n$ の $S^n$ への作用も誘導します。
例えば、 $\sigma=\left(1\ 2\ 3\ 4\ 5\ 6 \right)\in D_6$ 、 $\tau=(2\ 6)(3\ 5)\in D_6$ により、
$\begin{eqnarray} &&\sigma\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left({\rm E},\ {\rm C},\ {\rm O},\ {\rm F},\ {\rm E},\ {\rm E} \right)\\ &&\tau\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left({\rm C},\ {\rm E},\ {\rm E},\ {\rm F},\ {\rm F},\ {\rm O} \right) \end{eqnarray}$
などなどです。
さて、この作用 $D_6\times S^6\longrightarrow S^6$ に対して、
$\begin{eqnarray} &&e\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)\quad \sigma\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm E},\ {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E}\right)\\ &&\sigma^2\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm E},\ {\rm E},\ {\rm C},\ {\rm O},\ {\rm F},\ {\rm F}\right)\quad \sigma^3\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm F},\ {\rm E},\ {\rm E},\ {\rm C},\ {\rm O},\ {\rm F}\right)\\ &&\sigma^4\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm F},\ {\rm F},\ {\rm C},\ {\rm E},\ {\rm C},\ {\rm O}\right)\quad \sigma^5\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E},\ {\rm C}\right)\\ &&\tau\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm C},\ {\rm E},\ {\rm E},\ {\rm F},\ {\rm F},\ {\rm O}\right)\quad \sigma\tau\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm O},\ {\rm C},\ {\rm E},\ {\rm E},\ {\rm F},\ {\rm F}\right)\\ &&\sigma^2\tau\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm F},\ {\rm O},\ {\rm C},\ {\rm E},\ {\rm E},\ {\rm F}\right)\quad \sigma^3\tau\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm F},\ {\rm F},\ {\rm O},\ {\rm C},\ {\rm E},\ {\rm E}\right)\\ &&\sigma^4\tau\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm E},\ {\rm F},\ {\rm F},\ {\rm O},\ {\rm C},\ {\rm E}\right)\quad \sigma^5\tau\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\left( {\rm E},\ {\rm E},\ {\rm F},\ {\rm F},\ {\rm O},\ {\rm C}\right)\\ \end{eqnarray}$
です。
これは ${\rm C}\leftrightarrow{\rm O}\leftrightarrow{\rm F}\leftrightarrow{\rm F}\leftrightarrow{\rm E}\leftrightarrow{\rm E}$ という順序に並べたアルファベットを何処かの文字から初めて、連続して文字を読んだときに得られる文字列の全体の集合です。
別の言い方をすれば、円順列において、 $\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)$ と同一視されるような順列の全体の集合です。
このとき、軌道空間 $D_6\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)$ は
$D_6\cdot\left( {\rm C},\ {\rm O},\ {\rm F},\ {\rm F},\ {\rm E},\ {\rm E}\right)=\{\left( X_1,\dots,X_6\right)\mid{\rm X_1}\leftrightarrow{\rm X_2}\leftrightarrow{\rm X_3}\leftrightarrow{\rm X_4}\leftrightarrow{\rm X_5}\leftrightarrow{\rm X_6}と\\ {\rm C}\leftrightarrow{\rm O}\leftrightarrow{\rm F}\leftrightarrow{\rm F}\leftrightarrow{\rm E}\leftrightarrow{\rm E}は同じ順列\}$
となります。

例3.(具体的、というわけでは無いかもしれませんが)
ざっくりと述べます。
軌道空間は力学系と密接な関係があります。
ここで、力学系とは、「時間」、「状態空間」、「時間発展のルール」の３つ組のことだ、と言えます。
つまり、群(または半群) $G$ の空間 $X$ への作用 $\psi:F\times X\longrightarrow X,\ (g,x)\mapsto\psi(g,x)$ が
$\begin{eqnarray} &&\psi(e,x)=x,\quad (\forall x\in X)\\ &&\psi(gh,x)=\psi\left( h,\psi(g,x)\right)\quad (\forall x\in X,\ \forall g,h\in G) \end{eqnarray}$
で与えられると、 $G$ を時間、 $X$ を状態空間、 $\psi$ を時間発展のルールとするような力学系が定まるといいます。
状態空間の点 $x\in X$ が、ある「状態」を表すとすれば、その $G$ による軌道空間 $Gx=\left\{ \psi(g,x)\mid g\in G\right\}$ は時間とともに状態がどのように変化するか、ということを表現します。
例えば、時間 $G$ として加法群 $\mathbb{Z}$ を取りましょう。この場合、 $\psi_e:\{e\}\times X\longrightarrow X$ という写像を考えると、軌道は
$Gx=\mathbb{Z}x=\left\{ \psi_e^k(e,x)\middle|k\in \mathbb{Z}\right\}$
となり、状態 $x$ の時間 $k$ 後の状態が $\psi_e^k(e,x)$ です。
ただし、 $\psi_e^k(e,x)$ は $\psi_e(e,x)$ の $k$ 回の合成写像です。
時間が $\mathbb{R}$ であり、 $\psi$ が連続写像であれば、軌道は $\mathbb{R}$ の連続写像による像、すなわち曲線となります。

返信

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34