本記事の内容
本記事は群作用について解説する記事です。
本記事を読むに当たり、群、商群(剰余群)について知っている必要があるため、以下の記事も合わせて御覧ください。
↓群の記事
↓商群(剰余群)の記事
ちょっと小咄
「群作用とは何か?」という話をする前に、群作用の応用としてシロー(Sylow)の定理があります。
シローの定理は有限群を調べる上で、基本的な道具です。
後に解説する有限アーベル(可換)群の基本定理の証明にもシローの定理を使います。
群作用とは?
まずは群作用の大雑把な意味を述べます。
群作用の大雑把な意味
群作用を大雑把に一言で述べれば、
です。
これだけ読んでも、「どういうことだ?」となるかと思いますが、シローの定理やらを学んでいくと意味がわかってくると思います。
より詳しくは後の記事で群作用が出てきた際に再度説明します。
群作用とは?(数学的な話)
群作用を数学的に述べます。
群作用
\(G\)を群、\(X\)を集合とする。\(G\)の\(X\)への左作用とは、写像\(\varphi:G\times X\ni (g,x)\mapsto \varphi(g,x)\in X\)であり、次の性質1.、2.を満たすものをいう。- \(\varphi(1_G,x)=x\)
- \(\varphi(g,\varphi(h,x))=\varphi(gh,x)\)
- \(\psi(x,1_G)=x\)
- \(\psi\left(\psi(x,g),h\right)=\psi\left(x,gh \right)\)
\(G\)の\(X\)への作用が存在するとき、\(G\)は\(X\)に作用するという。左作用なら、\(G\)は\(X\)に左から作用するという。右作用も同様である。
結局、群作用の正体は写像です。
しかし、群の演算のときもお話しましたが、写像の言葉で書くと少々見にくいと思われますので、写像の部分を少々省略した形で再掲することにします。
群作用\(\varphi:G\times X\longrightarrow X\)に対して\(\varphi(g,x)\)を\(gx\)と書き、\(\psi:X\times G\longrightarrow X\)に対して\(\psi(x,g)\)を\(xg\)と書いたとします。
すると、
群作用
\(G\)を群、\(X\)を集合とする。\(G\)の\(X\)への左作用とは、次の性質1.、2.を満たす写像\(\varphi:G\times X\longrightarrow X\)をいう。ただし、\(\varphi(g,x)=gx\)と書くことにする。- \(1_Gx=x\)
- \(g(hx)=(gh)x\)
- \(1_Gx=x\)
- \((xg)h=x(gh)\)
\(G\)の\(X\)への作用が存在するとき、\(G\)は\(X\)に作用するという。左作用なら、\(G\)は\(X\)に左から作用するという。右作用も同様である。
と言い換えることができます。
\(G\)が\(X\)に左から作用し、\(x,y\in X\)、\(g\in G\)、\(gx=y\)なら、\(g\)により\(x\)は\(y\)に移るといいます。
群の演算と混乱しやすいので注意です。
先のように、群作用における\(\varphi(g,x)\)を\(gx\)と簡易的に記述すると、「群の演算に見える」という気もします(筆者は誤認したことがあります)。
そこで、重要になってくるのが、「群作用は写像である」ということです。
写像を構成する要素として定義域と終域があります。
群の演算の定義域は\(G\times G\)で、群の作用の定義域は\(G\times X\)であるという違いがあります。
故に、\(gx\)という記号が出てきたらば、定義域を確認することで群の演算なのか、それとも作用なのかを判断する必要があります。
\(x\in X\)を\(gx \in G\times X\)に写す写像は全単射です。
定理1.
群\(G\)が集合\(X\)に作用すると、\(g\in G\)に対して定まる写像\(X\ni x\mapsto gx\in X\)は全単射である。定理1.の証明
\(G\)が\(X\)に左から作用し、\(x,y\in X\)、\(g\in G\)、\(gx=y\)なら、\(g\)により\(x\)は\(y\)に移るというのでした。
このとき、
$$
g^{-1}gx=1_Gx=x=g^{-1}y
$$
となります。
つまり、\(g\)により\(x\)が\(y\)に移るなら、\(g^{-1}\)により\(y\)は\(x\)に移ります。
あるいは言い方を変えて、\(x\)に戻ります。
\(g^{-1}\)による作用が\(g\)による作用の逆写像となっているため、定理1.が成り立ちます。
定理1.の証明終わり
群作用の例
いくつか群作用の例を挙げます。
例1.(自明な作用)
\(G\)を群、\(X\)を集合とします。
\(g\in G\)、\(x\in X\)に対して\(gx=x\)と定めると(写像の言葉で言えば\(\varphi(g,x)=x\)で定めると)、これは左作用でもあり、右作用でもあります。
この作用のことを自明な作用といいます。
例2.
\(G=\mathcal{G}_n\)、すなわち
とすると、\(\mathcal{G}_n\)は写像の合成で群となります。
これを置換群または対称群というのでした。
このとき、\(X=\left\{1,\dots, n\right\}\)とします。
\(G\)の要素は\(X\)から\(X\)への全単射から成っています。
\(\sigma\in G\)、\(i\in X\)に対して、\(\sigma(i)\)を写像としての値とすると、\(\sigma,\tau\in \mathcal{G}_n\)に対して、\((\sigma\tau)(i)=\sigma\left( \tau(i)\right)\)が\(G\)に定まった演算だったので、\((\sigma,i)\mapsto \sigma(i)\)は左作用です。
例3.(線型作用)
\(G\)を群、\(\rho:G\longrightarrow {\rm GL}_2(\mathbb{R})\)を準同型写像とします。
ここで、
でしたので、
です。
\(\mathbb{R}^2\)を、実数を成分に持つ2次元の列ベクトルの成す実線型空間とします。
\(g\in G\)なら、\(\rho(g)\)は\((2,2)\)型の行列なので、\(\boldsymbol{x}\in \mathbb{R}^2\)に対して演算\(\rho(g)\boldsymbol{x}\)を定めることが出来ます。
\(\rho\)は準同型なので、\(\rho(1_G)=I_2\)(2次元の単位行列)です。
従って、\(\rho(1_G)\boldsymbol{x}=\boldsymbol{x}\)となります。
また、\(g,h\in G\)なら、行列の積に関しては結合則が成り立つので、
$$
\rho(g)\left( \rho(h)\boldsymbol{x}\right)\left(\rho(g)\rho(h) \right)\boldsymbol{x}=\rho(gh)\boldsymbol{x}
$$
となります。
従って、\((g,\boldsymbol{x})\mapsto \rho(g)\boldsymbol{x}\)は左作用です。
各\(\rho(g)\)は線型写像なので、このような作用のことを線型な作用といいます。
例3.についてもうちょっと踏み込んでみます。
\(G\)が\({\rm GL}_2(\mathbb{R})\)の部分群なら、包含写像\(G\longrightarrow {\rm GL}_2(\mathbb{R})\)は準同型です。
故に、\(G\)は\(\mathbb{R}^2\)に作用します。
特に、直交群\(O(2)\)について考えてみます。
ここで、直交群について少々説明します。
行列\(A\)に対して、その転置行列を\(A^\top\)と書きます。
行列\(A,B\)の積が定まるなら、\((AB)^\top=B^\top A^\top\)でした。
また、\(A\in{\rm GL}_n(\mathbb{R})\)なら、\((A^\top)^{-1}=\left( A^{-1}\right)^\top\)です。
\(G={\rm GL}_n(\mathbb{R})\)、
$$
H=\left\{g\in G\middle|g^\top g=I_n\right\}
$$
とします。
勿論、\(I_n\in H\)です。
\(g,h\in H\)なら、
$$
(gh)^\top(gh)=h^\top g^\top gh=h^\top(g^\top g)h=h^\top I_nh=h^\top h=I_n
$$
なので、\(gh\in H\)です。
また、\(g^\top=g^{-1}\)となるので、\(g g^\top=I_n\)です。
故に、
$$
(g^{-1})^\top g^{-1}=(g^\top)^{-1}g^{-1}=(gg^\top)^{-1}=I_n^{-1}=I_n
$$
となるので、\(g^{-1}\in H\)です。
従って、\(H\)は\(G\)の部分群です。
この\(H\)のことを直交群といいます。
直交群
$$ H=\left\{g\in G\middle|g^\top g=I_n\right\} $$ を\(O(n)\)と書き、直交群という。\(SO(n)=O(n)\cap {\rm SL}_n(\mathbb{R})\)とおき、特殊直交群という。先の考察から、\(g\in O(n)\)ならば、\(g^\top\in O(n)\)です。
さて、直交群\(O(2)\)に対する考察に戻りましょう。
\(\theta\in\mathbb{R}\)に対して、
$$
R_\theta=
\begin{pmatrix}
\cos\theta&-\sin\theta\\
\sin\theta&\cos\theta
\end{pmatrix}\tag{1}
$$
とします。
\(R_\theta\in SO(2)\)だということは計算するとわかります。
\(R_\theta\)により、ベクトル\(\displaystyle\left(\begin{array}{c}1\\0\end{array}\right),\left(\begin{array}{c}0\\1\end{array}\right)\)はそれぞれ\(\displaystyle\left(\begin{array}{c}\cos\theta\\ \sin\theta\end{array}\right),\left(\begin{array}{c}-\sin\theta\\ \cos\theta\end{array}\right)\)に移ります。
従って、\(R_\theta\)は角度\(\theta\)の回転を表しています。
補題2.
$$SO(2)=\left\{R_\theta\middle|\theta\in\mathbb{R}\right\}$$補題2.の証明
\(\displaystyle g=\begin{pmatrix}a&b \\c&d\end{pmatrix}\in SO(2)\)であれば、\(a^2+c^2=1\)、\(b^2+d^2=1\)、\(ab+cd=0\)となります。
従って、\(a=\cos\theta\)、\(c=\sin\theta\)となる\(\theta\in\mathbb{R}\)が存在します。
\(ab+cd=0\)なので、\(b=-t\sin\theta\)、\(d=t\cos\theta\)となる\(t\in\mathbb{R}\)が存在します。
\(\det g=1\)なので、\(t=1\)となり、\(g=R_\theta\)です。
補題2.の証明終わり
補題2.は、\(SO(2)\)が回転により\(\mathbb{R}^2\)(平面)に作用しているということを主張しています。
\(g\in O(2)\)なら、\(g^\top g=I_2\)の行列式を考えると、\(\left( \det g\right)^2=1\)です。
故に\(\det g=\pm1\)です。
$$
r=
\begin{pmatrix}
1&0\\
0&-1
\end{pmatrix}\in O(2)
$$
ですので、\(\det :O(2)\longrightarrow \left\{\pm1\right\}\)は全射準同型です。
ここで、準同型定理を使います。
定理0.(準同型定理(第一同型定理))
\(\varphi:G\longrightarrow H\)を群の準同型とする。\(\pi:G\longrightarrow G/{{\rm Ker}(\varphi)}\)を自然な準同型写像とするとき、以下の図が可換図式となるような準同型写像\(\psi:G/{{\rm Ker}(\varphi)}\longrightarrow H\)が唯一つ存在し、\(\psi\)は\(G/{{\rm Ker}(\varphi)}\)から\({\rm Image}(\varphi)\)への同型となる。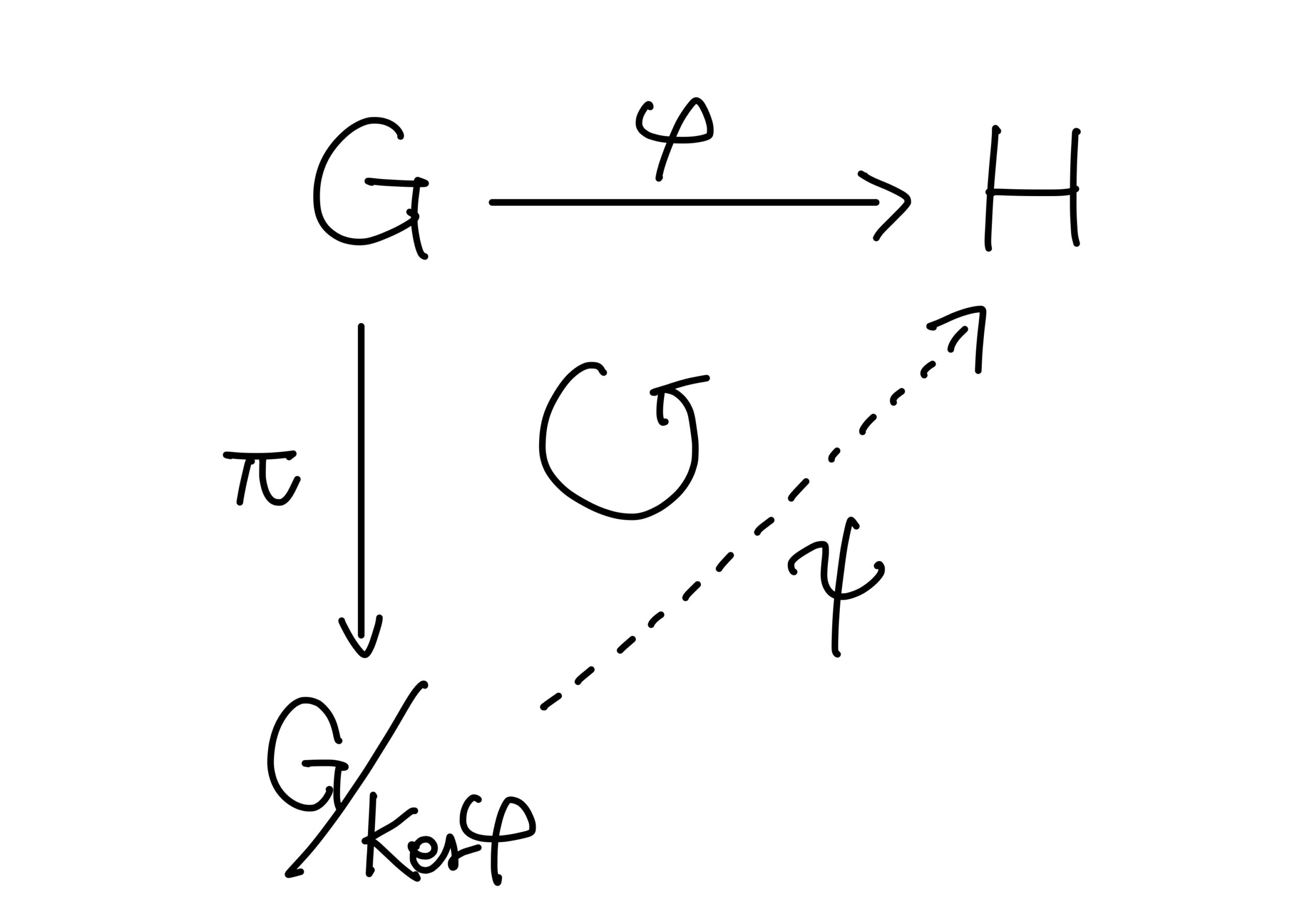
準同型定理の証明は【代数学の基礎シリーズ】群論編 その5を御覧ください。
\({\rm Ker}(\det)=SO(2)\)なので、準同型定理から、\(O(2)/{SO(2)}\cong\left\{\pm1\right\}\)です。
従って、\(SO(2)\)の\(O(2)\)における指数\(O(2):SO(2)\)は2です。
\(r\)はベクトル\(\displaystyle\left(\begin{array}{c}x\\ y\end{array}\right)\)を\(\displaystyle\left(\begin{array}{c}x\\ -y\end{array}\right)\)に移します。
つまり、\(x\)軸に対して対称な点に移す作用です。
例3.では2次元の場合を考えましたが、\(G\longrightarrow {\rm GL}_n(\mathbb{R})\)が準同型写像である場合も同様で、\(G\)は\(\mathbb{R}^n\)に作用します。
従って、\(O(n)\)、\(SO(n)\)も\(\mathbb{R}^n\)に作用します。
また、準同型\(G\longrightarrow {\rm GL}_n(\mathbb{C})\)があれば、\(G\)は\(\mathbb{C}^n\)に左から作用しています。
この場合も線型な作用といいます。
皆様のコメントを下さい!
今回はデカルトです。
デカルトの時代は、大航海時代以後に世界を制覇していたスペイン、ポルトガルが次第に衰え、フランス、オランダ、イギリスなどの新興勢力に取って代わられる過渡期でした。
フランスでは、新旧のキリ スト教徒が争ったフランスの宗教戦争(1562-1598)が収拾され、近代国家として秩序が整いつつある頃です。
時代の雰囲気は、一言で言えばアレクサンドル・デュマ(Dumas, Alexandre;1802-1870)の小説『三銃 士』に象徴されます。
デカルトはフランスのアンドル・エ・ロワールで生まれました。
0歳のときからイエズス会が運営するラ・フレーシュ学院に入り、スコラ哲学、論理学、自然学などを学びましたが、就中、特に興味を抱いたのは数学です。
メルセンヌは学院での先輩であり、終生の友人でした。
〇デカルトは近世哲学の父ともよばれます。
スコラ哲学の教育を受けましたが、それへの不満からアリストテレスの自然哲学に代わる新しい自然哲学を建設しようと企て、直観と演繹による科学方法論を提唱しました。
〇一般に、スコラ学とは11世紀以降にキリスト教神学者・哲学者などの学者たちによって採られた学問のスタイルを指し、問題に対する解答を導き出し、矛盾を解決することを目標としています。
スコラはSchool(学校)の同源語です。
アンセルム(St. Anselm;1033-1109)やトマス・アクィナスが代表的なスコラ学者です。
如何でしたか?
デカルトについてここに書いてあることの他にご存知のことがあれば、是非コメントで教えて下さい!
結
今回は、群作用について解説しました。
群作用は今後方程式論に関わってくる重要な概念です。
シローの定理は群作用の応用です。
次回は群作用についてもう少し踏み込んでみます。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
代数についてより詳しく知りたい方は以下を参考にすると良いと思います!





コメントをする
右作用の定義の2.が上下で逆になってるかもしれません♂️
名無し様
ご指摘ありがとうございます。
修正いたしました。