本記事の内容
本記事は「準同型定理(第一同型定理)」を証明する記事です。
本記事を読むにあたり、準同型写像と商群(剰余群)について知っている必要があるため、以下の記事も合わせてご覧ください。
↓準同型写像の記事
↓商群(剰余群)の記事
準同型写像と商群の軽い復習
前回解説した準同型写像と商群の軽い復習をします。
準同型写像
準同型写像
2つの群\(G_1\)、\(G_2\)の間の写像\(\phi:G_1\longrightarrow G_2\)は、群の構造を保つとき、すなわち- 任意の\(g,h\in G_1\)に対して\(\phi(gh)=\phi(g)\phi(h)\)である。
- 任意の\(g\in G_1\)に対して\(\phi(g^{-1})=\phi(g)^{-1}\)である。
- \(\phi(1_{G_1})=1_{G_2}\)である。
詳しくは、【代数学の基礎シリーズ】群論編 その3を御覧ください。
核(kernel)
核(kernel)
\(G_1\)、\(G_2\)を群、\(\phi:G_1\longrightarrow G_2\)を準同型写像とする。このとき $$ {\rm Ker}(\phi)=\left\{x\in G_1\middle|\phi(x)=1_{G_2}\right\} $$ を準同型写像\(\phi\)の核(kernel)という。詳しくは、【代数学の基礎シリーズ】群論編 その3を御覧ください。
左剰余類、右剰余類
左剰余類、右剰余類
\(H\subset G\)を群\(G\)の部分群、\(x,y\in G\)とする。- 左剰余類 群\(G\)上の関係\(\sim_1\)を $$ x\sim_1 y\Longleftrightarrow x^{-1}y\in H $$ で定めると、\(\sim_1\)は同値関係である。 このとき、\(x\in G\)の同値類を\(xH\)と書き、\(x\in H\)の\(H\)による左剰余類という。 この同値関係による商集合、すなわち\(G/{\sim_1}\)を\(G/{H}\)と書く。
- 右剰余類 群\(G\)上の関係\(\sim_2\)を $$ x\sim_2 y\Longleftrightarrow yx^{-1}\in H $$ で定めると、\(\sim_2\)も同値関係である。 このとき、\(x\in G\)の同値類を\(Hx\)と書き、\(x\in H\)の\(H\)による右剰余類という。 この同値関係による商集合、すなわち\(G/{\sim_2}\)を\(H\backslash{G}\)と書く。
詳しくは、【代数学の基礎シリーズ】群論編 その4を御覧ください。
商群(剰余群)
商群(剰余群)
\(N\)を群\(G\)の部分群とする。左剰余類\(G/{N}\)は演算 $$ G/{N}\times G/{N}\ni \left( gN,hN\right)\mapsto ghN\in G/{N} $$ により群となる。この\(G/{H}\)を\(G\)の\(N\)による商群(quotient group)または剰余群(factor group)と呼ぶ。詳しくは、【代数学の基礎シリーズ】群論編 その4を御覧ください。
準同型定理(第一同型定理)とは?
準同型定理は群論において最も重要と言っても過言ではないほどの定理です。
実際、群論の講義のゴールとして準同型定理を挙げていたりします。
準同型定理は、群の間の準同型写像があたえられたとき、その準同型写像による核と像とを関連付ける定理です。
早速、主張を明示します。
定理0.(準同型定理(第一同型定理))
\(\varphi:G\longrightarrow H\)を群の準同型とする。\(\pi:G\longrightarrow G/{{\rm Ker}(\varphi)}\)を自然な準同型写像とするとき、以下の図が可換図式となるような準同型写像\(\psi:G/{{\rm Ker}(\varphi)}\longrightarrow H\)が唯一つ存在し、\(\psi\)は\(G/{{\rm Ker}(\varphi)}\)から\({\rm Image}(\varphi)\)への同型となる。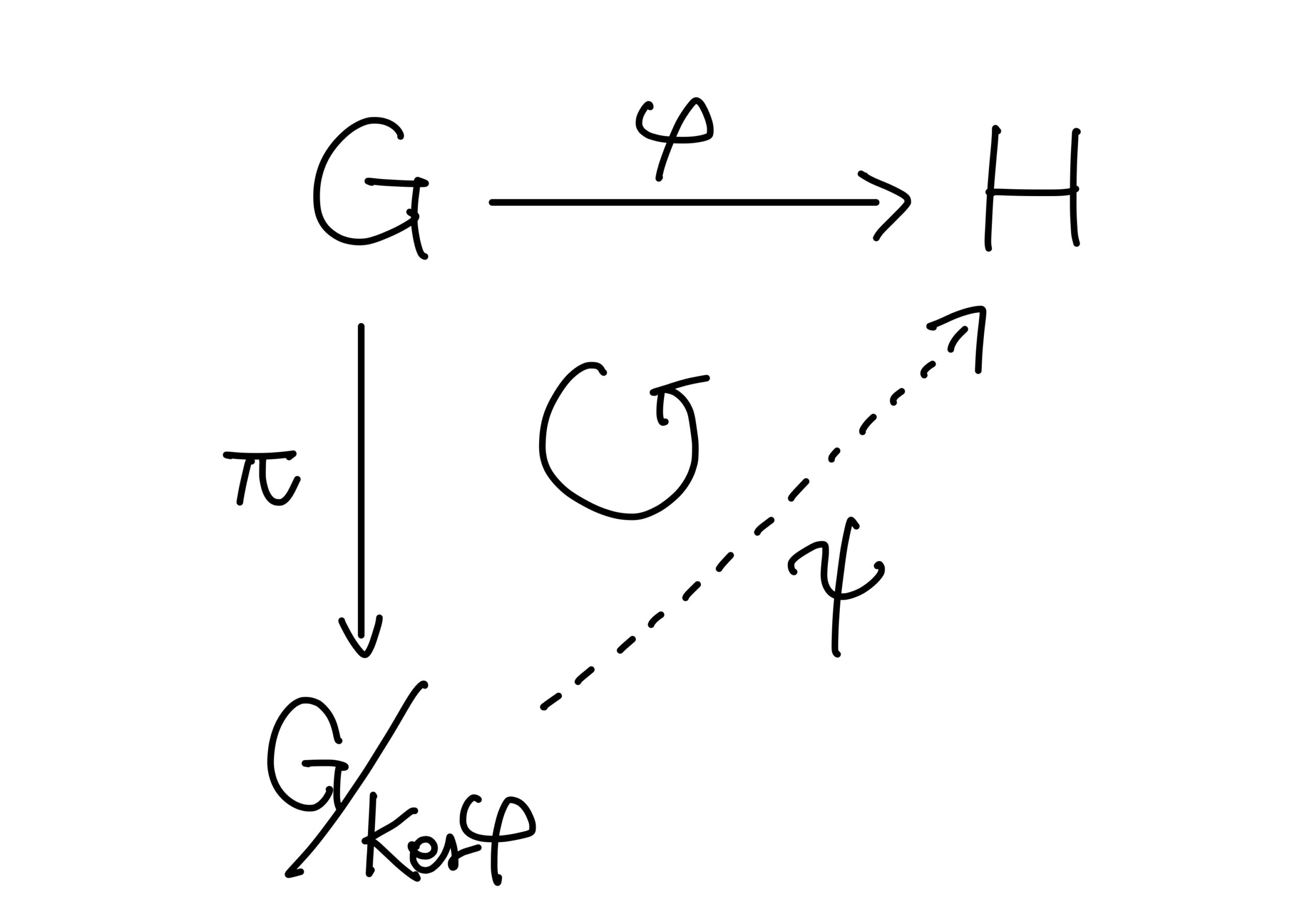
準同型定理(第一同型定理)の証明
では証明します。
準同型定理(第一同型定理)の証明
①\(\psi\)を定め、それがwell-definedであることの証明
\(g\in G\)に対して、写像\(\psi:G/{{\rm Ker}(\varphi)}\longrightarrow H\)を
$$
\psi\left( g{\rm Ker}(\varphi)\right)=\varphi(g)
$$
で定めます。
ここで、以下の事実を使います。
定理1.
\(G_1\)、\(G_2\)を群、\(\phi:G_1\longrightarrow G_2\)を準同型写像とする。このとき、\({\rm Ker}(\phi)\triangleleft G_1\)、すなわち\(\phi\)の核\({\rm Ker}(\phi)\)は\(G_1\)の正規部分群である。定理1.の証明は【代数学の基礎シリーズ】群論編 その3を御覧ください。
定理1.により、\({\rm Ker}(\varphi)\)は正規部分群であるため、\({\rm Ker}(\varphi)\)は群\(H\)の部分群です。
故に\({\rm Ker}(\varphi)\)は結合律を満たし、かつ\(n\in {\rm Ker}(\varphi)\)であれば\(\varphi(n)=1_G\)であるので
$$
\varphi(gn)=\varphi(g)\varphi(n)=\varphi(g)1_G=\varphi(g)
$$
です。
従って、\(\psi\)は剰余類\(g{\rm Ker}(\varphi)\)の代表元のとり方に依存せずに定まります。
つまり、\(\psi\)は写像としての体裁が整っています(これをwell-definedと言ったのでした)。
②定めた\(\psi\)が準同型写像であることの証明
\(g,h\in G\)であれば、商群\(G/{{\rm Ker}(\varphi)}\)の演算と、\(G\)が群なので結合律を満たすことから
\begin{eqnarray}
\psi\left( \left( g{\rm Ker}(\varphi)\right)\left( h{\rm Ker}(\varphi)\right)\right)&=&\psi\left( gh{\rm Ker}(\varphi)\right)\\
&=&\varphi(gh)\\
&=&\varphi(g)\varphi(h)\\
&=&\psi\left( g{\rm Ker}(\varphi)\right)\psi\left( h{\rm Ker}(\varphi)\right)
\end{eqnarray}
となるので、\(\psi\)は準同型写像です。
またこのとき、\(\varphi=\psi\circ \pi\)です。
実際、\(\varphi\)と\(\psi\circ \pi\)の定義域と終域が一致しており、任意の\(g\in G\)に対して、
$$
\left(\psi\circ \pi \right)(g)=\psi\left(\pi(g) \right)=\psi\left( g{\rm Ker}(\varphi)\right)=\varphi(g)
$$
だからです。
ただし、\(\pi:G\longrightarrow G/{{\rm Ker}(\varphi)}\)は自然な写像なので、任意の\(g\in G\)に対して
$$
\pi(g)=g{\rm Ker}(\varphi)
$$
です。
③定めた\(\psi\)が同型写像(全単射な準同型写像)であることの証明
\(\psi\left( g{\rm Ker}(\varphi)\right)=\varphi(g)\)と定めたので、\(\psi\left( g{\rm Ker}(\varphi)\right)=1_H\)であれば、\(\varphi(g)=1_H\)です。
故に\(g\in{\rm Ker}(\varphi)\)となり、\(g{\rm Ker}(\varphi)={\rm Ker}(\varphi)\)です。
従って、\(g{\rm Ker}(\varphi)={\rm Ker}(\varphi)\)は\(G/{{\rm Ker}(\varphi)}\)の単位元です。
ここで、次の事実を使います。
定理2.
準同型写像\(\phi:G_1\longrightarrow G_2\)が単射であるための必要十分条件は、\({\rm Ker}(\phi)=\left\{1_{G_1}\right\}\)となることである。定理2.の証明は【代数学の基礎シリーズ】群論編 その3を御覧ください。
定理2.から\(\psi:G/{{\rm Ker}(\varphi)}\longrightarrow H\)は単射です。
\(g\in G\)であれば、\(\varphi(g)=\psi\left( g{\rm Ker}(\varphi)\right)\)であるので、\({\rm Image}(\psi)s\subset{\rm Image}(\psi)\)です。
\(G/{{\rm Ker}(\varphi)}\)の任意の要素は\(g{\rm Ker}(\varphi)\)という形をしているので、\({\rm Image}(\varphi)\subset {\rm Image}(\varphi)\)ということも分かります。
故に、\({\rm Image}(\psi)={\rm Image}(\varphi)\)だから\(\psi\)は全射です。
\(\psi\)は単射だったので、全射かつ単射だから\(\psi\)は全単射です。
従って、\(\psi\)は準同型写像だったので、\(\psi\)は同型写像だから、\(G/{{\rm Ker}(\varphi)}\)と\({\rm Image}(\psi)={\rm Image}(\varphi)\)は\(\psi\)で同型です。
④\(\psi\)が一意的に存在することの証明
\(\psi\)が\(\psi\circ \pi=\varphi\)という条件を満たせば、\(g\in G\)に対して、\(\psi\left( g{\rm Ker}(\varphi)\right)=\varphi(g)\)と値が定まるので、\(\psi\)は一意的です。
準同型定理(第一同型定理)の証明終わり
準同型定理(第一同型定理)のキモチ(軽く)
準同型定理のキモチを例から見てみます。
\(\mathbb{R}^3\)はベクトルの和を演算として群で、\(\mathbb{R}\)は実数のたし算を演算として群です。
ここで、写像\(\varphi:\mathbb{R}^3\longrightarrow \mathbb{R}\)を、
$$
\varphi(x,y,z)=x+y+z
$$
で定めます。
このとき、\(\varphi\)は準同型写像です。
実際、任意の\((x_1,y_1,z_1),(x_2,y_2,z_2)\in\mathbb{R}^3\)に対して
\begin{eqnarray}
\varphi((x_1,y_1,z_1)+(x_2,y_2,z_2)^{-1})&=&\varphi((x_1,y_1,z_1)-(x_2,y_2,z_2))\\
&=&\varphi\left( x_1-x_2,y_1-y_2,z_1-z_2\right)\\
&=&(x_1-x_2)+(y_1-y_2)+(z_1-z_2)\\
&=&(x_1+y_1+z_1)-(x_2+y_2+z_2)
\end{eqnarray}
だからです。
このとき、
$$
{\rm Ker}(\varphi)=\left\{(x,y,z)\in \mathbb{R}^3\middle| x+y+z=0\right\}
$$
で、また\({\rm Image}(\varphi)=\mathbb{R}\)です。
ここで、\(k\in\mathbb{R}\)に対して、
$$
S_k=\left\{(x,y,z)\in\mathbb{R}^3\middle|x+y+z=k\right\}
$$
としましょう。
すると、\((x_k,y_k,z_k)\in S_k\)、\((x^\prime_k,y^\prime_k,z^\prime_k)\in S_k\)とすると、
$$
(x_k-x^\prime_k,y_k-y^\prime_k,z_k-z^\prime_k)\in{\rm Ker}(\varphi)
$$
です。
従って、\(S_k\)は同値類です。
準同型定理から、\(\mathbb{R}^3/{{\rm Ker}(\varphi)}\cong\left\{S_k\middle|k\in\mathbb{R}\right\}\)です。
このとき、\(S_k\)が動くのは\(\mathbb{R}\)だけで、これは平面を表しています。
準同型定理は\(\mathbb{R}^3/{{\rm Ker}(\varphi)}\)と\(\left\{S_k\middle|k\in\mathbb{R}\right\}\)が群として同じものだ、ということを主張していますので、これは「空間は平面を積み重ねたもの」ということを示している、ということになります。
皆様のコメントを下さい!
今回はパスカルです。
パスカル(Blaise Pascal;1623-1662)はフランスの数学者、物理学者、宗教哲学者です。
確率論のパイオニアでもあり、幾何学でも重要な貢献を行いました。
計算機の発明(1642年)でも有名です。
早熟の天才であり、家庭で教育を受けました。
16歳(1640年)のとき、『円錐曲線試論』を発表。
これはわずか1ページの論文で、デザルグの影響を色濃く受けています。
1648年には、これを発展させて『円錐曲線論』を完成しました。
没後、その原稿を見たライプニッツがパスカルの甥に出版を勧めたものの、そのままになり、原稿は惜しくも散逸してしまいました。
妹のひとりがポール・ロワヤル修道院に入ったことに影響され、キリスト教信仰に深く帰依して、人生の途中で宗教活動に入りました。
「人間は考える葦である」という言葉で有名な著述「パンセ」は、死後に刊行されたものです。
パスカルの思想はデカルトの合理主義と対比されますが、自然科学の研究では、むしろデカルトより合理的です。
「哲学をばかにすることこそ、真に哲学することである」という言葉がこれを象徴しています。
如何でしたか?
パスカルと言えば、筆者は物理で出てくる圧力の単位を連想します。
ここに書かれている事のほかにでパスカルについてご存知のことがあれば是非コメントで教えて下さい!
結
今回は準同型定理(第一同型定理)の証明を解説しました。
準同型定理は、群論において最も重要と言っても過言ではないほどの定理です。
実際、群論の講義のゴールとして準同型定理を挙げていたりします。
準同型定理は、群の間の準同型写像があたえられたとき、その準同型写像による核と像とを関連付ける定理です。
次回は部分群の対応に関する準同型定理について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
代数についてより詳しく知りたい方は以下を参考にすると良いと思います!





コメントをする