本記事の内容
本記事は第三同型定理の証明と準同型の分解について解説する記事です。
本記事を読むにあたり、準同型定理について知っている必要があるため、以下の記事も合わせてご覧ください。
第三同型定理の証明
まずは主張を明確にします。
第三同型定理の明示
定理1.(第三同型定理)
\(G\)を群、\(N\subset N^\prime\)を\(G\)の正規部分群とするとき、次の1.、2.が成り立つ。- 準同型\(\varphi:G/{N}\longrightarrow G/{N^\prime}\)で、、\(\varphi(xN)=xN^\prime\)となるものが存在する。
- \(\left( G/{N}\right)/{\left(N^\prime/{N} \right)}\cong G/{N^\prime}\)である。
第三同型定理の証明
では、早速証明していきます。
第三同型定理の証明
(1)の証明
\(x\in G\)、\(y\in N\)ならば、\(N\subset N^\prime\)なので、\(xyN^\prime=xN^\prime\)です。
故に、\(\varphi(xN)=xN^\prime\)とすると、\(\varphi\)は\(G/{N}\)から\(G/{N^\prime}\)へのwell-definedな写像になります(写像として体裁が整っています)。
\(\varphi\)が準同型写像となるのは、任意の\(x,y\in G\)に対して
$$
\varphi(xNyN)=\varphi(xyN)=xyN^\prime=xN^\prime yN^\prime
$$
となるからです。
(2)の証明
準同型定理を使います。
定理0.(準同型定理(第一同型定理))
\(\varphi:G\longrightarrow H\)を群の準同型とする。\(\pi:G\longrightarrow G/{{\rm Ker}(\varphi)}\)を自然な準同型写像とするとき、以下の図が可換図式となるような準同型写像\(\psi:G/{{\rm Ker}(\varphi)}\longrightarrow H\)が唯一つ存在し、\(\psi\)は\(G/{{\rm Ker}(\varphi)}\)から\({\rm Image}(\varphi)\)への同型となる。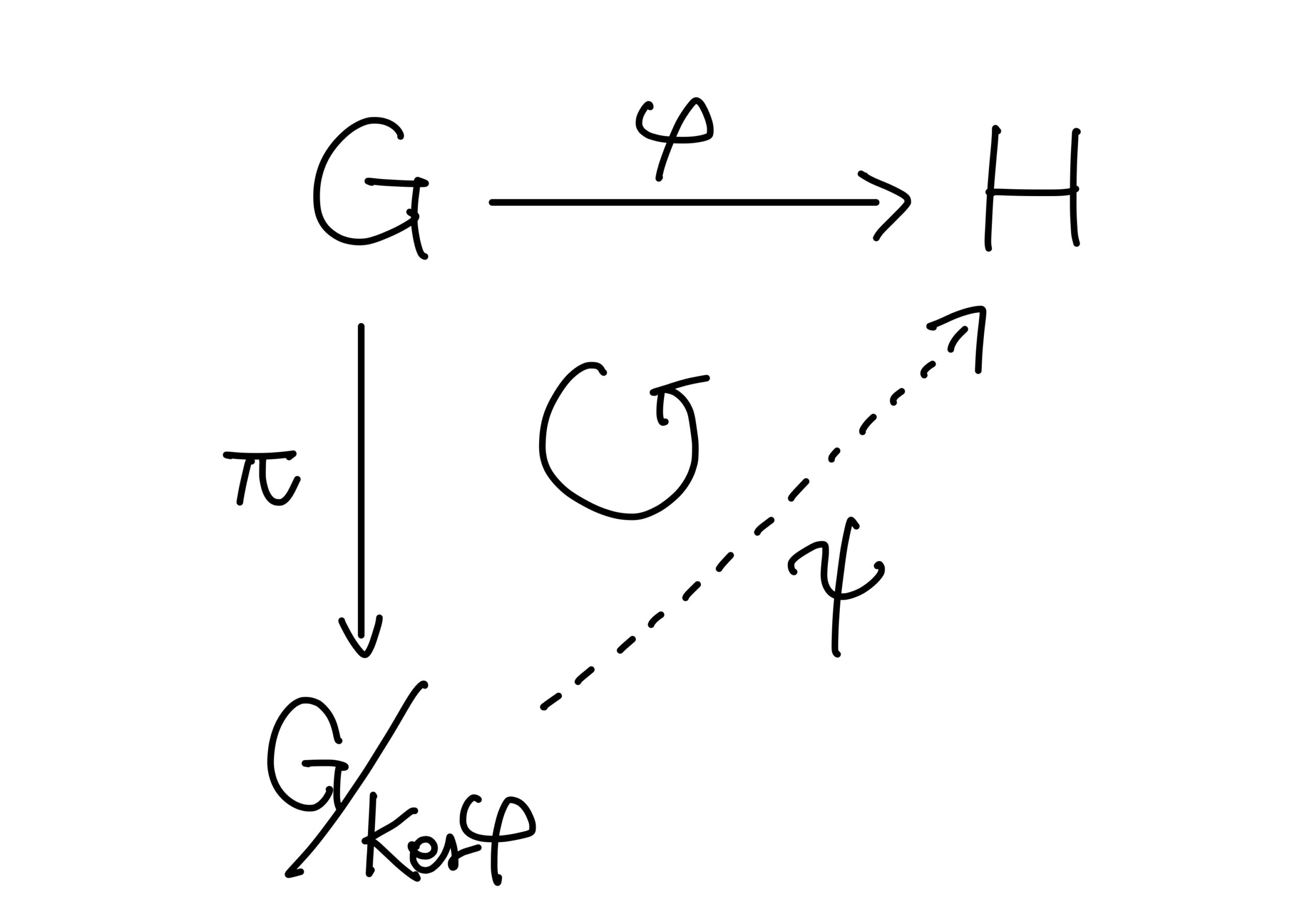
定理0.(準同型定理)の証明は【代数学の基礎シリーズ】群論編 その5を御覧ください。
\({\rm Ker}(\varphi)=N^\prime/{N}\)となるので、定理0.(準同型定理)から2.を得ます。
第三同型定理の証明終わり
第三同型定理の言いたいこととしては、商群同士の割り算において、約分のようなことができる、という定理です。
第三準同型定理に出現する準同型写像\(G/{N}\longrightarrow G/{N^\prime}\)を自然な準同型といいます。
準同型の分解
主張を明示します。
主張の明示
定理2.(準同型の分解)
\(\varphi:G\longrightarrow H\)を群の準同型とする。\(N\subset G\)が正規部分群なら、\(\pi:G\longrightarrow G/{N}\)を自然な準同型とするとき、下図が可換図式となるような準同型\(\psi:G/{N}\longrightarrow H\)が存在するための必要十分条件は\(N\subset {\rm Ker}(\varphi)\)となることである。
定理2.の証明
定理2.の条件を満たすような\(\psi\)が存在したとします。
\(\varphi=\psi\circ \pi\)なので、\(N={\rm Ker}(\pi)\subset {\rm Ker}(\varphi)\)です。
逆に、\(N\subset {\rm Ker}(\varphi)\)だとすると、\(N^\prime={\rm Ker}(\varphi)\)とおくと、先程証明した第三同型定理から、\(x\in G\)ならば、\(f(xN)=xN^\prime\)となる準同型\(f:G/{N}\longrightarrow G/{N^\prime}\)が存在します。

再度準同型定理から、準同型\(\psi^\prime:G/{{\rm Ker}(\varphi)}\longrightarrow H\)で、\(\pi^\prime:G\longrightarrow G/{{\rm Ker}(\varphi)}\)を自然な準同型とするとき、\(\varphi=\psi^\prime\circ f\circ \pi\)です。
従って、\(\psi=\psi^\prime\circ f\)とすればOKです。
定理2.の証明終わり
皆様のコメントを下さい!
今回はフィボナッチです。
フィボナッチ(1170年頃–1250年頃)はイタリアの数学者であり、フルネームはレオナルド=フィリオ=ボナッチ(Fibonacci)。
フィボナッチは「ボナッチの息子」を意味する愛称です。
ピサの出身ということから、ピサのレオナルド(Leonardo de Pisa)ともよばれます。
エジプト、シリア、ギリシャ、シシリーなどに旅行し、その間にアラビア数学を含む多くの知識を吸収しました。
1202年にフィボナッチが発行した『算盤の書』(Liber Abaci) はアラビア数学の真髄とインドの記数法 をヨーロッパに紹介した先駆的な書物です(1202 年)。
フィボナッチ数列の名称は。『算盤の書』の中で扱われていたことに由来します(古くにはインドの数学書にも記載されていました)。
如何でしたか?
平清盛が没したのが1181年ですから、そのくらいに生きていた人物です。
なんとすごいことでしょうか。
ここに書かれている事のほかにでフィボナッチについてご存知のことがあれば是非コメントで教えて下さい!
結
今回は第三同型定理と準同型写像の分解の証明を解説しました。
これらも群論において最も重要と言っても過言ではないほどの定理です。
実際、群論の講義のゴールとしてこれらの定理を挙げていたりします。
第三同型定理は、商群同士の割り算で、約分のようなことができる、という定理です。
次回は三次方程式の解法について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
代数についてより詳しく知りたい方は以下を参考にすると良いと思います!




コメントをする
φ=π∘πなので、N=Ker(π)⊂Ker(φ)です,とありますが、φ=ψ∘πが正しいのではないでしょうか。
質問です。https://www.math.kyoto-u.ac.jp/~yukie/alg-closure.pdfをご覧ください。代数閉包の存在の別証明と題されたPDFファイルです。F’の存在が矛盾を示すとありますが、Fの存在でも矛盾が示せるのではないでしょうか。FはL_0の自明でない代数拡大である、とありますが代数拡大は拡大体を意味するのだから、L_0の自明でない代数拡大である、とはL_0<Fを意味するのではないか、と思うわけです。
質問する指導者がいなくて困っているところです。
naru様
コメントありがとうごさいます。
返信が遅れてしまい誠に申し訳ございません。
お答えいたします。
>φ=π∘πなので、N=Ker(π)⊂Ker(φ)です,とありますが、φ=ψ∘πが正しいのではないでしょうか。
naru様のご指摘の通り、\(\varphi=\psi\circ \pi\)でした。修正いたしました。
ご指摘ありがとうございました。
>質問です。https://www.math.kyoto-u.ac.jp/~yukie/alg-closure.pdfをご覧ください。代数閉包の存在の別証明と題されたPDFファイルです。F’の存在が矛盾を示すとありますが、Fの存在でも矛盾が示せるのではないでしょうか。FはL_0の自明でない代数拡大である、とありますが代数拡大は拡大体を意味するのだから、L_0の自明でない代数拡大である、とはL_0
ご回答ありがとうございました。私のスマホからは、「代数閉包の存在の別証明」のご回答が表示されないのですが、ご回答を拝見することは可能でしょうか。
naru様
代数閉体の部分のご質問へのコメントが途中で切れてしまっておりました。
改めてこちらで回答させていただきます。
pdfを拝見いたしました。
疑問に思っていらっしゃる部分は\(L_0\)が代数閉体であることの証明の部分かと存じます。
結論から申しますと、pdfに書かれている証明法で正解です。
この部分の証明の大まかな流れは以下です。
①\(L_0\)が\(Y\)の極大元であるとき、\(L_0\)が代数閉体であることを背理法で示す。
↓
②\(L_0\)が代数閉体でないと仮定。
↓
③\(L_0\)が代数閉体でないことから、\(2\)次以上の既約多項式\(f(x)\in L_0[x]\)が存在。
↓
④存在する\(f(x)\in L_0[x]\)を用いた\(F:=L_0[x]/\left(f(x) \right)\)は\(L_0\)の代数拡大。
↓
⑤\(F^\prime:=L_0\cup i\left(F\setminus L_0 \right)\)は\(L_0< F^\prime\)とみなせる。
↓
⑥しかしこれは\(L_0\)の極大性に矛盾。
です。
つまり、\(F\)の存在は、背理法の仮定「\(L_0\)が代数閉体でない」の範疇です。
故に、\(F\)の存在自体(\(F^\prime\)の存在もですが)はあくまで背理法の仮定から得られる主張であって、矛盾させる対象ではないということになります。
平たく言えば、「\(L_0\)が代数閉体でないことを仮定して話をすすめると、\(L_0\)が代数閉体でないことから別の代数拡大が得られ(\(F^\prime\))、その存在が\(L_0\)の極大性に矛盾する。」ということになります。
したがって、ご提示いただいたpdfの証明方法で正解です。
お示ししてくださった証明の要約は、私も一応追うことができます。追加コメントで引っかかりがあります。
①(F’の存在もですが)…矛盾させる対象ではない。
②(F’)、その存在が…矛盾する
言葉遣いに誤読を招きやすいところはありませんか。F’は「矛盾させ」ないのか、「矛盾する」のか、どちらが言いたいのか読み取りにくいです。
質問のお答えになっていないような気がします。「L_0が代数閉体でないことから別の代数拡大が得られ(F’)、その存在がL_0の極大性に矛盾する」とあります。「その存在」とは、別の代数拡大の存在と読め、証明の要約で「FはL_0の代数拡大」と書いていることから、F’ではなくFでも矛盾が示せるのではないかという当初の疑問は残ります。
naru様
先程の群のご質問のところで書き忘れてしまいました。
例のpdf関する質問ですが、数日お待ちいただければ幸いです….
「数学ガール」流に言わせていただくと、準同型の分解を示せてso what?
意義などを聞かせてほしい。
naru様
続けてご回答させていただきます。
私個人の印象といたしましては、準同型の分解は「群の表示(ブログでは”生成元と関係式で定義された群”として紹介しています)」に使われていることが最たる応用例だと感じています。
群の表示はトポロジーでよく見かける概念という印象があります(専門分野ではないのであくまで印象ですが)。
群の表示は「群を構成する要素(生成元のこと)と群の間の関係(関係式)を”一括して調べてしまう”ことで、その背景にある性質を見えやすくする」というものです。
群の表示の性質として、以下があります。
定理.
\(G\)は\(n\)個の生成元\(y_1,\dots,y_n\)を持ち、関係式
$$
R_1(y_1,\dots,y_n)=\dots=R_m(y_1,\dots,y_n)=1_G
$$
を持つとする。このとき、
$$
K=\left\langle x_1,\dots,x_n\middle|R_1(\boldsymbol{x})=1,\ \dots,R(\boldsymbol{x})=1\right\rangle
$$
から\(G\)への、\(\varphi(x_1)=y_1,\cdots,\varphi(x_n)=y_m\)を満たす全射準同型\(\varphi\)が存在する。
(群論編 その30を御覧ください。)
これにより、全射準同型の存在が分かり、位数の決定につながります。
早く知りたいのでよろしくお願いします。
こんにちは。あまりに些細な質問で申し訳ありませんが、定理2の証明の冒頭部分の
N=Ker(π)⊂Ker(φ)
ですが、なぜそうのような関係になるのかわかりません。よろしければ、ご説明頂けませんでしょうか。よろしくお願い致します。
トエダ様
コメントありがとうございます。
>定理2の証明の冒頭部分のN=Ker(π)⊂Ker(φ)ですが、なぜそうのような関係になるのかわかりません。
というお問い合わせですが、お答えいたします。
まず、\(N={\rm Ker}(\pi)\)である理由ですが、それは次が成り立っているからです。
定理.
\(G\)を群、\(N\subset G\)を群\(G\)の正規部分群とする。このとき、自然な写像
$$
\pi:G\longrightarrow G/{N}
$$
は全射かつ準同型写像である。また、\({\rm Ker}(\pi)=N\)である。
前半については証明を省略します(この証明にご関心をお持ちであれば、再度お問い合わせください)。
\(1_G\)を\(G\)の単位元とします。
商群\(G/{N}\)の単位元は\(N\)ですから、\(g\in G\)に対して、\(\pi(g)=gN=N\)であることと\(g\in N=1_gN\)は同値です。したがって、\({\rm Ker}(\pi)=N\)です。
(この証明に不明点があれば、またお問い合わせください)
次に、\({\rm Ker}(\pi)\subset {\rm Ker}(\varphi)\)についてです。
今、仮定として
が可換図式となるような準同型写像\(\psi:G/{N}\longrightarrow H\)が存在しています。
示すべきは
$$
g^\prime\in N={\rm Ker}(\pi)\Longrightarrow g^\prime\in {\rm Ker}(\varphi)={\rm Ker}(\psi\circ \pi)
$$
です。
ここで、群\(H\)の単位元を\(1_H\)、\(G/N\)の単位元を\(1_{G/{N}}(=N)\)と書いたとすると
\begin{eqnarray}
&&{\rm Ker}(\varphi)={\rm Ker}(\psi\circ\pi)=\left\{ g\in G\middle|\left( \psi\circ\pi\right)(g)=1_H\right\}\\
&&{\rm Ker}(\pi)=\left\{ g^\prime\in G\middle|\pi(g^\prime)=1_{G/{N}}=N\right\}
\end{eqnarray}
であることに注意です。
さて、このとき\(g^\prime\in N={\rm Ker}(\pi)\)に対して\(\varphi(g^\prime)=\left( \psi\circ\pi\right)(g^\prime)=1_H\)であればOKです。
\(g^\prime\in N={\rm Ker}(\pi)\)ですから、\(\pi(g^\prime)=1_{G/{N}}=N\)であることを使えば、
\begin{eqnarray}
\varphi(g^\prime)&=&\left(\psi\circ\pi \right)(g^\prime)\\
&=&\psi\left( \pi(g^\prime)\right)\\
&=&\psi\left( 1_{G/{N}}\right)\\
&=&\psi\left(N \right)
\end{eqnarray}
です。
\(\psi:G/{N}\longrightarrow H\)は準同型写像ですので、\(G/{N}\)の単位元\(N\)は\(\psi\)で\(H\)の単位元\(1_H\)に写ります。
したがって、\(\psi(N)=1_H\)です。
故に、\(g^\prime\in N={\rm Ker}(\pi)\)に対して、\(\varphi(g^\prime)=\left( \psi\circ\pi\right)(g^\prime)=1_H\)が証明されたので、\(N={\rm Ker}(\pi)\subset {\rm Ker}(\varphi)\)です。
オノ様
雪江明彦さんの著書「整数論1」の「群論」の章の「準同型の分解」(p.122)を読み、証明の冒頭部分で「定理の条件を満たすψが存在したとすると。φ=ψ∘πなので、Ker(π)⊂Ker(φ)である。」の意味が理解できず、こちらのサイトに辿り着き、質問させて頂いた次第でした。
g′∈N=Ker(π),g′∈Ker(φ)は導出できたのですが、そこから g′∈N=Ker(π)⟹g′∈Ker(φ) を導出できなかったのですが、ご説明を噛み締めながら読み「Ker(π)⊂Ker(φ)」が成立していることが理解できました。
御説明頂き大変有り難うございました。