本記事の内容
本記事は点列と数列の商(点列と数列との割り算)の極限を解説する記事です。
本記事を読むにあたり、点列の極限と数列の極限について知っている必要があるため、その際は以下の記事を参照してください。
ではいきましょう!
点列の極限のチャラい復習
点列の極限についてより詳しく知りたい方は【解析学の基礎シリーズ】点列編 その1を御覧ください。
ここでは掻い摘んだ復習に留めます。
点列の極限をチャラく復習しましょう。
点列は数列の多次元バージョンでした。
つまり、数列の値は実数でしたが、点列の値はベクトルというわけでした。
数列の極限は極限(実数)への近づき方が直線的だったのに対して、点列の極限は極限(ベクトル)への近づき方が空間的(ありとあらゆる方向から近づく)なのでした。
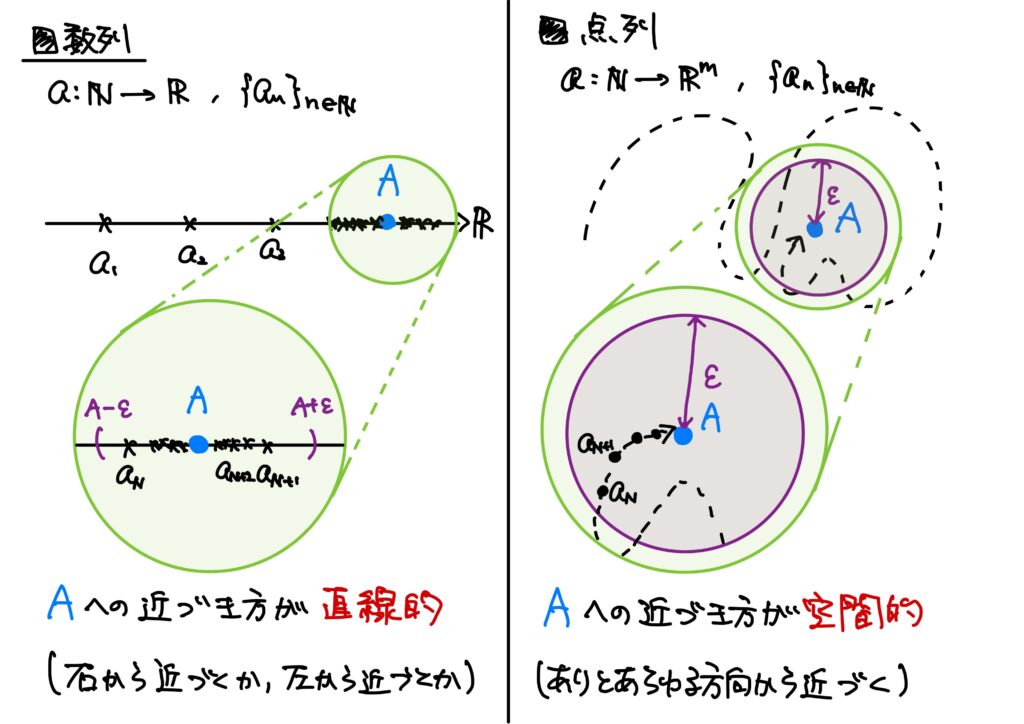
さらに、以下の定理が成り立つのでした。
つまり、点列の極限は数列の極限に帰着できる、ということでした。
ベクトルの商?
前回は点列の外積の極限と極限の外積が一致するということを説明しました。
ベクトルにおける積は実数の積のような単純な話ではなく内積、外積、ウェッジ積など色々ありました。
筆者と同年代の方は高校の数Cで行列を習うのですが、ベクトルは行列の一部だと思えば掛け算を考えることはできますが、それはベクトルの掛け算というより行列の掛け算です。
今回扱う「商」も比較的似ています。
つまり、ベクトルをベクトルで割るというベクトルにおける割り算は基本的に考えません。
勿論、無理やり割り算という演算規則を定めようとすることはできますが、その演算自体に意味があることはあまりありません。
そもそも割り算は掛け算の逆演算なので、掛け算が一筋縄でいかないのですから、割り算も一筋縄ではいけません。
従って、今回扱うのは「点列と数列の商の極限」です。
点列と数列の商の極限はどうなりそう?
まずは例を見てみましょう。
例1. 数列\(\{k_n\}_{n\in\mathbb{N}}\)が\(\displaystyle k_n=1+\frac{1}{n}\)で定められていて、点列\(\{\boldsymbol{a}_n\}_{n\in\mathbb{N}}\)が\(\displaystyle\{\boldsymbol{a}_n\}_{n\in\mathbb{N}}=\left(\frac{1}{n^2},\ \frac{2}{n}\right)^\top\)とします。
任意の\(n\in\mathbb{N}\)に対して\(k_n\neq0\)です。
このとき、
\begin{eqnarray}
\lim_{n\to\infty}\frac{1}{k_n}\boldsymbol{a}_n&=&\lim_{n\to\infty}\frac{1}{1+\frac{1}{n}}
\left(
\begin{array}{c}
\displaystyle\frac{1}{n^2} \\
\displaystyle\frac{2}{n} \\
\end{array}
\right)\\
&=&\lim_{n\to\infty}
\left(
\begin{array}{c}
\displaystyle\frac{1}{n^2+2n} \\
\displaystyle\frac{2}{n+2} \\
\end{array}
\right)\\
&=&
\left(
\begin{array}{c}
\displaystyle\lim_{n\to\infty}\frac{1}{n^2+2n} \\
\displaystyle\lim_{n\to\infty}\frac{2}{n+2} \\
\end{array}
\right)\\
&=&\left(
\begin{array}{c}
0\\
0\\
\end{array}
\right)\\
\end{eqnarray}
です。
ここで、
$$\lim_{n\to\infty}\frac{1}{n^2+2n}=\lim_{n\to\infty}\frac{2}{n+2}=0$$
です。
これの証明は「数列の収束って?」〜直感から論理へ〜【解析学の基礎シリーズ】を御覧ください(アルキメデスの原理を使うことで証明できます)。
一方で、
\begin{eqnarray}
\left(\frac{1}{\displaystyle\lim_{n\to\infty}k_n}\right)\cdot\lim_{n\to\infty}\boldsymbol{a}_n&=&\frac{1}{1}
\left(
\begin{array}{c}
0 \\
0 \\
\end{array}
\right)=\left(
\begin{array}{c}
0 \\
0 \\
\end{array}
\right)
\end{eqnarray}
従って一致します。
点列と数列の商の極限
では主張を明示しましょう。
証明
これは式変形することで証明できます。
\begin{eqnarray}
\lim_{n\to\infty}\frac{1}{k_n}\boldsymbol{a}_n&=&\lim_{n\to\infty}\frac{1}{k_n}
\left(
\begin{array}{c}
a_{n,1} \\
a_{n,2} \\
\vdots\\
a_{n,m}
\end{array}
\right)\\
&=&\lim_{n\to\infty}
\left(
\begin{array}{c}
\displaystyle\frac{a_{n,1}}{k_n} \\
\displaystyle\frac{a_{n,2}}{k_n} \\
\vdots\\
\displaystyle\frac{a_{n,m}}{k_n} \\
\end{array}
\right)\\
\end{eqnarray}
です。
ここで、定理(点列の収束と同値な命題)から
\begin{eqnarray}
\lim_{n\to\infty}
\left(
\begin{array}{c}
\displaystyle\frac{a_{n,1}}{k_n} \\
\displaystyle\frac{a_{n,2}}{k_n} \\
\vdots\\
\displaystyle\frac{a_{n,m}}{k_n} \\
\end{array}
\right)
=\left(
\begin{array}{c}
\displaystyle\lim_{n\to\infty}\frac{a_{n,1}}{k_n} \\
\displaystyle\lim_{n\to\infty}\frac{a_{n,2}}{k_n} \\
\vdots\\
\displaystyle\lim_{n\to\infty}\frac{a_{n,m}}{k_n} \\
\end{array}
\right)
\end{eqnarray}
です。
従って、任意の\(n\in\mathbb{N}\)に対して\(b_n\neq0\)かつ\(\displaystyle\lim_{n\to\infty}b_n\neq0\)が成り立つような収束する数列\(\{a_n\}_{n\in\mathbb{N}}\)と\(\{b_n\}_{n\in\mathbb{N}}\)に対して
$$\lim_{n\to\infty}\frac{a_n}{b_n}=\frac{\displaystyle\lim_{n\to\infty}a_n}{\displaystyle\lim_{n\to\infty}b_n}$$
が成り立てば、再度定理(点列の収束と同値な命題)を使うことで、
\begin{eqnarray}
\left(
\begin{array}{c}
\displaystyle\lim_{n\to\infty}\frac{a_{n,1}}{k_n} \\
\displaystyle\lim_{n\to\infty}\frac{a_{n,2}}{k_n} \\
\vdots\\
\displaystyle\lim_{n\to\infty}\frac{a_{n,m}}{k_n} \\
\end{array}
\right)&=&
\left(
\begin{array}{c}
\frac{\displaystyle\lim_{n\to\infty}a_{n,1}}{\displaystyle\lim_{n\to\infty}k_n} \\
\frac{\displaystyle\lim_{n\to\infty}a_{n,2}}{\displaystyle\lim_{n\to\infty}k_n} \\
\vdots\\
\frac{\displaystyle\lim_{n\to\infty}a_{n,m}}{\displaystyle\lim_{n\to\infty}k_n} \\
\end{array}
\right)=\frac{1}{\displaystyle\lim_{n\to\infty}k_n}
\left(
\begin{array}{c}
\displaystyle\lim_{n\to\infty}a_{n,1} \\
\displaystyle\lim_{n\to\infty}a_{n,2} \\
\vdots\\
\displaystyle\lim_{n\to\infty}a_{n,m} \\
\end{array}
\right)
=\frac{1}{\displaystyle\lim_{n\to\infty}k_n}\cdot
\lim_{n\to\infty}
\left(
\begin{array}{c}
a_{n,1} \\
a_{n,2} \\
\vdots\\
a_{n,m} \\
\end{array}
\right)\\
&=&\frac{1}{\displaystyle\lim_{n\to\infty}k_n}\cdot
\lim_{n\to\infty}\boldsymbol{a}_n
=\frac{\displaystyle\lim_{n\to\infty}\boldsymbol{a}_n}{\displaystyle\lim_{n\to\infty}k_n}
\end{eqnarray}
となり、証明完了です。
従って、次を示せば証明が終わります。
数列の商の極限の証明
今、
が成り立つため、収束する数列\(\{b_n\}_{n\in\mathbb{N}}\)に対して任意の\(n\in\mathbb{N}\)で\(b_n\neq0\)かつ\(B\neq0\)が成り立つならば、
$$\lim_{n\to\infty}\frac{1}{b_n}=\frac{1}{\displaystyle\lim_{n\to\infty}b_n}$$
が成り立つことを示せば証明完了です。
従って、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow \left|\frac{1}{b_n}-\frac{1}{B}\right|<\epsilon)$$
を示します。
さて、結局はある番号\(N\)を見つけたいわけです。
そのために、\(\displaystyle\left|\frac{1}{b_n}-\frac{1}{B}\right|\)を変形してみます。
\begin{eqnarray}
\left|\frac{1}{b_n}-\frac{1}{B}\right|=\left|\frac{B-b_n}{b_nB}\right|=\frac{|B-b_n|}{|b_n|\cdot|B|}
\end{eqnarray}
となります。
ここで、仮に、任意の\(n\in\mathbb{N}\)に対して\(|b_n|\geq L\)となる実数\(L\)が存在したとします。
すると、今、数列\(\{b_n\}_{n\in\mathbb{N}}\)は\(B\)に収束するので、
$$(\forall \epsilon_b>0)(\exists N_b\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N_b\Rightarrow |b_n-B|<\epsilon_b)$$
が成り立っています。
従って、
\begin{eqnarray}
\frac{|B-b_n|}{|b_n|\cdot|B|}\leq \frac{B-b_n}{|L|\cdot|B|}< \frac{\epsilon_b}{|L|\cdot|B|}
\end{eqnarray}
が成り立ちます。
\(\epsilon_b>0\)は任意なので、任意の\(\epsilon>0\)を使って\(\epsilon_b= \displaystyle|L|\cdot|B|\epsilon\)と帳尻合わせをすることで、
$$
\left|\frac{1}{b_n}-\frac{1}{B}\right|\leq\frac{\epsilon_b}{|L|\cdot|B|}<\epsilon
$$
が成り立ちます。
\(N\)として\(N_b\)を採用することで
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow \left|\frac{1}{b_n}-\frac{1}{B}\right|<\epsilon)$$
が成り立ち、証明は終わります。
故に、以下を示します。
補題の証明
実数列\(\{a_n\}_{n\in\mathbb{N}}\)が\(A\in\mathbb{R}\)に収束するとします。
つまり
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_n-A|<\epsilon)$$
が成り立っています。
つまり、\(n\geq N\)なる\(n\in\mathbb{N}\)に対しては
$$A-\epsilon<a_n<A+\epsilon$$
が成り立っています。
従って、\(|a_n|>|A-\epsilon|\)または\(|a_n|>|A+\epsilon|\)が成り立っています。
故に\(L’=\min{|A-\epsilon|,|A+\epsilon|}\)とすれば、
\(n\geq N\)なる\(n\in\mathbb{N}\)に対しては\(|a_n|>L’\)です。
次に、\(1\leq n< N\)という\(n\in\mathbb{N}\)について考えてみましょう。
\(1\leq n< N\)という\(n\in\mathbb{N}\)に対しては\(\{a_n\}\)の値は有限個です。
従って、\(L=\min\{|a_1|,|a_2|,\dots ,|a_{N-1}|,L’\}\)とすることで、\(1\leq n< N\)という\(n\in\mathbb{N}\)についても\(n\geq N\)という\(n\in\mathbb{N}\)についても、すなわち任意の\(n\in\mathbb{N}\)に対して\(|a_n|\geq L\)です。
補題の証明終わり
この補題が正しいことが示されたので、\(\displaystyle\lim_{n\to\infty}\frac{1}{b_n}=\frac{1}{\displaystyle\lim_{n\to\infty}b_n}\)が成り立つこと、すなわち
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow \left|\frac{1}{b_n}-\frac{1}{B}\right|<\epsilon)$$
が成り立つことが証明されました。
故にこの事実と数列の極限の積から数列の商の極限が成り立ちます。
数列の商の極限の証明終わり
数列の商の極限が成り立ったので、点列と数列の商の極限が成り立ちます。
点列と数列の商の極限の証明終わり
結
今回は点列と数列の症の極限が極限の商と一致することを示しました。
和差積と同様に商の場合も点列の極限は結局数列の極限に帰着できます。
次回は閑話休題ということで、筆者が普段使っているペンについて紹介します。
「折角勉強するなら一緒にノートを取りませんか?」という話です。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする