本記事の内容
本記事は関数の発散、特にある点付近での関数の発散について解説する記事です。
本記事を読むにあたり、数列の発散で述べた「無限大」を知っている必要があるため、その際は以下の記事を参照してください。
また、関数の収束についても知っている必要があるため、その際は以下の記事を参照してください。
関数の発散と数列の発散の違いは?
数列と同様に関数にも「発散」があります。
「数列と同じだよ」と言いたいところですが、若干違います。
何が違うのか、というと数列は「最終的に値はどうなるの?」とうことだけに興味があるのに対して、関数は「この点付近で値はどうなるの?」ということにも興味があるからです。
それ故関数には連続性という概念があります。
記号で書けば
- 数列:\(n\to\infty\)のみ。
- 関数:\(x\to a\)(ある点付近の値は?)、\(x\to\infty\)(最終的に値はどうなる?)
ということです。
今回は、\(x\to a\)での発散、すなわち\(x\to a\)のときの\(f(x)\to\infty\)について解説します。
ある点付近での発散って?
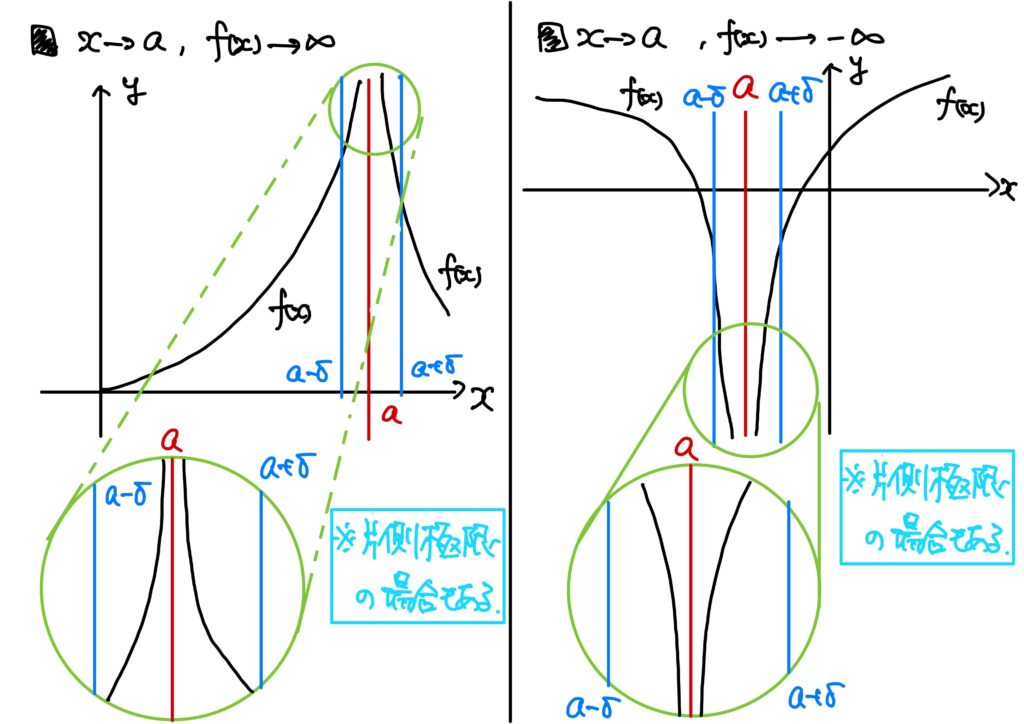
\(x\to a\)のときの\(f(x)\to\infty\)を一言でのべれば、次です。
「ある点の付近」というのは、「ある点\(a\)との距離が\(\delta\)未満であるような\(x\)に対しては」という意味です。(関数の収束と同じだネ)
“無限大”とはどんな実数よりも大きい数でした。
詳しくは【解析学の基礎シリーズ】数列の発散編 その2を参照してください。
ちなみに、負の無限大も同じです。
以上のことを論理式で書くと以下になります。
- \(\infty\)への発散 関数\(f\)が\(x\to a\)のとき\(\infty\)(正の無限大)に発散するとは、次が成り立つことをいう。 $$(\forall U\in\mathbb{R})(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-a|<\delta\Rightarrow f(x)>U)$$ このとき、 $$\lim_{x\to a}f(x)=\infty$$ と書く。
- ある点付近での\(\infty\)への発散 関数\(f\)が\(x\to a\)のとき\(-\infty\)(負の無限大)に発散するとは、次が成り立つことをいう。 $$(\forall L\in\mathbb{R})(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-a|<\delta\Rightarrow f(x)<L)$$ このとき、 $$\lim_{x\to a}f(x)=-\infty$$ と書く。
では、実際に証明してみましょう。
例9
\(f:\mathbb{R}\setminus\{0\}\to\mathbb{R}\)が\(\displaystyle f(x)=\frac{1}{x^2}\)で定められているとします。
このとき、\(\displaystyle\lim_{x\to 0}\frac{1}{x^2}=\infty\)です。
※注意※ 以前の記事(【解析学の基礎シリーズ】関数の極限編 その4)の例4.で述べたとおり、\(\displaystyle \lim_{x\to a}f(x)\)と\(f(a)\)は必ずしも一致しません。
今回の場合、そもそも\(0\)は定義域外なので、代入すらできません。
形式的に代入したとしても\(\displaystyle \frac{1}{0}\)で、高校数学での知識で「これは\(\infty\)でしょ?」と思うかもしれませんが、そもそも\(\infty\)は実数ではないのであくまで形式的です。
若干余談ではありますが、\(\infty\)は記号であって実数を表しているわけではありません。
言うなれば\(\infty\)という記号は単体ではほぼ意味は有りません。
\(f(x)\to\infty\)やら\(n\to\infty\)やら\([0,\infty)\)やら\(\displaystyle \lim_{x\to a}f(x)=\infty\)と書くことで初めて意味がある文字列になります。
従って、\(\displaystyle \frac{1}{0}=\infty\)はあくまで形式的に過ぎない、単なるイメージということです。
証明
示したいことは
$$(\forall U\in\mathbb{U})(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x|<\delta\Rightarrow \frac{1}{x^2}>U)$$
です。
つまり、上記を満たすような\(\delta>0\)を見つけこれれば良いわけです。(いつもの流れです。)
いつものように、結局は\(\delta\)を見つけたいわけですので、「もしそういう\(\delta>0\)があったらば…」ということで進めてみましょう。
もし、任意の\(U>0\)に対して上記を満たすような\(\delta>0\)があったとしたら、
\begin{eqnarray}
\frac{1}{x^2}=\frac{1}{|x|^2}>\frac{1}{\delta^2}
\end{eqnarray}
ですから、任意の\(\displaystyle \frac{1}{\delta^2}=U\)という方程式を解くことで\(\delta\)が求まるな、となるわけです。
これを解けば、\(\displaystyle \delta=\frac{1}{\sqrt{U}}\)とすれば良い事がわかります。
従って、任意の\(U\in\mathbb{R}\)に対して、\(\delta=\dfrac{1}{\sqrt{U}}\)とすると、\(\delta>0\)です。
\(0<|x|<\delta\)を満たすような任意の\(x\in\mathbb{R}\setminus\{0\}\)に対して、
\begin{eqnarray}
\frac{1}{x^2}&=&\frac{1}{|x|^2}>\frac{1}{\delta^2}=\frac{1}{\left(\frac{1}{\sqrt{U}} \right)^2}=U
\end{eqnarray}
です。
従って、$$(\forall U\in\mathbb{U})(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x|<\delta\Rightarrow \frac{1}{x^2}>U)$$
が成り立ったので、\(\displaystyle\lim_{x\to 0}\frac{1}{x^2}=\infty\)です。
証明終わり
結
今回は\(x\to a\)のときの\(f(x)\to\infty\)を解説しました。
どういうことかを一言でのべれば、次です。
数列のときと同様にどんな実数よりも大きいときに発散するというわけです。
次回は\(x\to\infty\)のときの発散について解説します。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!





コメントをする