本記事の内容
本記事は、「正四面体群は4次交代群と同型」であることを解説する記事です。
本記事を読むにあたり、対称群(置換群)、正多面体群について知っている必要があるため、以下の記事も合わせてご覧ください。
↓対称群(置換群)の記事
↓正多面体群の記事
軽い復習
対称群(置換群)
は写像の合成を演算として群でした。
この\(\mathcal{G}_X\)は特別な呼び名があり、置換群、または対称群と呼びます。
これは、まさに以前線型代数の記事で解説した置換が、写像の合成でもって群であるということです。
置換とは以下でした。
置換
\(n\in\mathbb{N}\)とする。\(n\)個の文字\(1,2,\dots,n\)からなる集合を $$ M_n=\{1,2,\dots,n\} $$ とする。写像\(\sigma:M_n\to M_n\)が全単射であるとき、\(\sigma\)を\(M_n\)の置換という。置換\(\sigma\)による対応が $$ 1\mapsto i_1,\ 2\mapsto i_2,\dots,n\mapsto i_n $$ であるとする、すなわち、 $$ \sigma(1)=i_1,\ \sigma(2)=i_2,\dots,\ \sigma(n)=i_n $$ とする。このとき\(\sigma\)を $$ \sigma= \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix} $$ と書く。
詳しくは【線型代数学の基礎シリーズ】行列式編 その1を御覧ください。
\(X=M_n\)のとき、\(\mathcal{G}_X\)を\(\mathcal{G}_n\)と書きます。
正多面体群
正多面体群を一言で表すと、
です。
ここで注意なのが、正多面体群の要素は正多面体ではないということです。
筆者だけかも知れませんが「正多面体群」という字面を見ると「正多面体自体が群になるのかな?」と思うかもしれません。
しかし違います。
あくまで正多面体をその同じ正多面体に写すような変換(写像)が要素です。
正多面体群
正多面体\(\mathcal{P}_i\ (i=4,6,8,12,20)\)に対して、- 合同変換 \(\mathcal{P}_i\)を\(\mathbb{R}^3\)内の単位球面に内接させる。このとき原点を中心とする回転のうち、頂点を頂点に写すものを\(\mathcal{P}_i\)の合同変換という。
- 正多面体群 \(\mathcal{P}_i\)の合同変換\(\sigma\)の逆回転\(\sigma^{-1}\)もまた合同変換であり、合同変換\(\sigma,\tau\)を続けて行った変換(\(\tau\sigma\)と書く)もまた合同変換である。故に合同変換全体は、変換の合成(写像の合成)を演算として群をなす。この群を正\(i\)面体群という。また、正二面体群と合わせてこれらをまとめて正多面体群という。
正八面体の各辺の中点を結ぶと立方体になります。
また、正二十面体の各辺の中点を結ぶと正十二面体になります。
したがって、正八面体群と立方体群は同型で、正二十面体群と正十二面体群は同型です。
正四面体群、正八面体群、正二十面体群をそれぞれ\({\rm T},\ {\rm O},\ {\rm I}\)(tetrahedron、octahedron、icosahedronの頭文字)と書きます。
詳しくは、【代数学の基礎シリーズ】群論編 その44を御覧ください。
正八面体群は4次対称群と同型
主張を明示します。
定理1.
\({\rm O}\cong \mathcal{G}_4\)である。すなわち、正八面体群は4次対称群と同型である。証明の前に少し補足します。
4次対称群は4次の置換の集合ですので、定理1.は「正八面体の頂点は回転や対称を駆使すればどの点にも移ることができる」といっているわけです。
定理1.の証明
\(F_1,\ F_2,\ F_3,\ F_4\)を正八面体の1つの頂点\({\rm P}\)に集まる面で、この順番に隣り合うように取ります(以下の図を参照)。
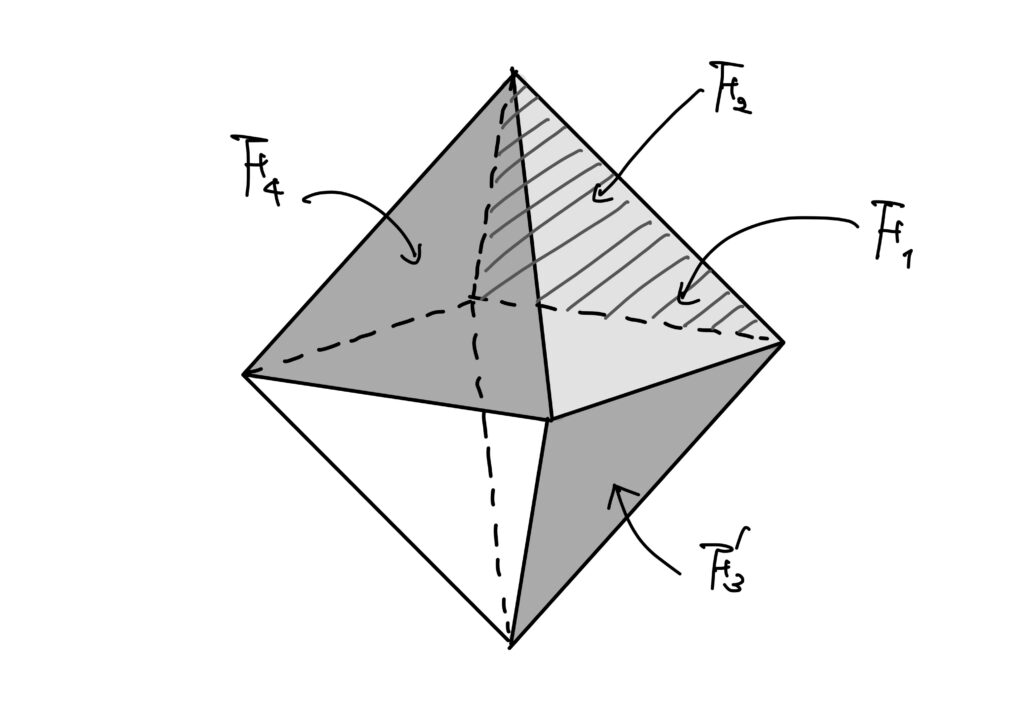
\(F_1^\prime,\ F_2^\prime,\ F_3^\prime,\ F_4^\prime\)をそれぞれ\(F_1,\ F_2,\ F_3,\ F_4\)に向かい合う面として、
\begin{eqnarray}
&&C_1=\left\{F_1,F_1^\prime\right\},\quad &&C_2=\left\{F_2,F_2^\prime\right\}\\
&&C_3=\left\{F_3,F_3^\prime\right\},\quad &&C_4=\left\{F_4,F_4^\prime\right\}
\end{eqnarray}
とします。
正八面体群\({\rm O}\)は集合\(\left\{C_1,\ C_2,m\ C_3,\ C_4\right\}\)に作用します。
ここで、群作用とは以下でした。
群作用
\(G\)を群、\(X\)を集合とする。\(G\)の\(X\)への左作用とは、写像\(\varphi:G\times X\ni (g,x)\mapsto \varphi(g,x)\in X\)であり、次の性質1.、2.を満たすものをいう。- \(\varphi(1_G,x)=x\)
- \(\varphi(g,\varphi(h,x))=\varphi(gh,x)\)
- \(\varphi(1_G,x)=x\)
- \(g(hx)=xgh)\)
\(G\)の\(X\)への作用が存在するとき、\(G\)は\(X\)に作用するという。左作用なら、\(G\)は\(X\)に左から作用するという。右作用も同様である。
詳しくは、【代数学の基礎シリーズ】群論編 その11を御覧ください。
故に、置換表現(後で復習します)\(\rho:{\rm O}\longrightarrow\mathcal{G}_4\)が定まります。
ここで、作用により定まる置換表現とは以下でした。
置換表現
群\(G\)が有限集合\(X=\left\{x_1,\dots,x_n\right\}\)に左から作用するとする。このとき $$ g\cdot x_i=x_{\rho(g)(i)}\quad (g\in G,\ i=1,\dots,n) $$ として定めると、\(\rho:G\longrightarrow \mathcal{G}_n\)は準同型写像である。この\(\rho\)を\(X\)への作用により定まる置換表現という。詳しくは、【代数学の基礎シリーズ】群論編 その13を御覧ください。
さて、このとき、\({\rm P}\)のまわりの回転は\(C_1\longrightarrow C_2\longrightarrow C_3\longrightarrow C_4\longrightarrow C_1\)という置換を引き起こします。
したがって、\((1\ 2\ 3\ 4)\in\rho\left( {\rm O}\right)\)です。
先程の図で面\(F_1\)の3つの辺が隣り合うように回転させれば、この回転は\({\rm O}\)の要素であり、\(F_2\longrightarrow F_4\longrightarrow F_3^\prime\longrightarrow F_2\)と置換します。
故に、この要素は\(C_2\longrightarrow C_4\longrightarrow C_3\longrightarrow C_2\)という置換を引き起こします。
したがって、\((2\ 4\ 3)\in\rho\left( {\rm O}\right)\)です。
同様にして、\(\rho\left( {\rm O}\right)\)は全ての3次の巡回置換を含むことが分かります。
ここで、次の事実を使います。
補題2.
\(n\geq3\)ならば、交代群\(A_n\)は長さ\(3\)の巡回置換で生成される。補題2.の証明は【代数学の基礎シリーズ】群論編 その42を御覧ください。
補題2.から\(\rho\left( {\rm O}\right)\)は4次交代群\(A_4\)(以下で復習)を含みます(\(\rho\left( {\rm O}\right)\supset A_4\))。
交代群の復習
交代群を一言で述べれば、\(\sigma\)を置換とし、\({\rm sgn}(\sigma)\)を\(\sigma\)の符号とすると、\({\rm sgn}\)は\(\mathcal{G}_n\)から\(\left\{\pm1\right\}\)への準同型写像となります。
\(A_n={\rm Ker}({\rm sgn})\)(準同型写像\(\varphi\)の核\({\rm Ker}(\varphi)\)は正規部分群でしたね)と書き、\(A_n\)のことを\(n\)次交代群といいます。
\((1\ 2\ 3\ 4)\)は奇置換なので、\(\rho\left( {\rm O}\right)=\mathcal{G}_4\)です。
ここで、次の事実を使います。
命題3.
\({\rm T},\ {\rm O},\ {\rm I}\)をそれぞれ正四面体群、正八面体群、正二十面体群とする。このとき- \(\left|{\rm T}\right|=12\).
- \(\left|{\rm O}\right|=24\).
- \(\left|{\rm I}\right|=60\).
命題3.の証明は【代数学の基礎シリーズ】群論編 その45を御覧ください。
命題3.の2.から\(\left|{\rm O}\right|=24\)なので、\(\rho\)は同型写像です。
定理1.の証明終わり
皆様のコメントを下さい!
今回は背理法に付随する事柄ついて語ります。
前回は、背理法が存在証明に使われる、と言う話をして、素数が無限個存在することの証明と抽斗論法の証明をしました。
しかしながら、抽斗論法はある種「当たり前」で、このような事実がいつ役に立つのか疑わしいものです。
今回は、どういう場合で役に立つのかということを紹介します。
まず、小手調べとして次の問題を解いてみて下さい。
\(n+1\)個の自然数\(a_1,a_2,\cdots,a_n\)が与えられているとき、差\(a_i-a_j\ (i\neq j)\)のうちの少なくとも1つは\(n\)により割り切れる。これを抽斗論法を用いて示せ。
(ヒント:\(a_i\)たちを\(n\)で割った余りを見る)
証明
割り算定理(後のシリーズで証明します)から、\(a_i=q_in+r_i\ (0\leq r_i<n)\)と書けます。
このとき、\(n+1\)個の「もの」\(r_1,\cdots,r_{n+1}\)(「もの」の正体は”余り”)は\(n\)個の「抽斗」\(0,1,\cdots,n-1\)に入っているから、\(r_i=r_j\)となるような\(i\neq j\)が存在することになります。
故に、\(a_i-a_j\)は\(n\)で割り切れます。
証明終わり
今の問題を見れば分かるように、抽斗論法自身は「当たり前」のことでもそれをどのように適用するかは(すなわち、「もの」と「抽斗」をどのように設定するかは)まったく明らかでないことを示しています。
証明は省略しますが、以下の主張も抽斗論法で証明することができます。
\(a\)を正の無理数とする。このとき、任意の自然数\(N\)に対して $$ N\geq m,\quad \left|ma-n\right|<\frac{1}{N} $$ を満たす自然数\(m\)と整数\(n\geq0\)が存在する。特に、 $$ \left|a-\frac{n}{m}\right|<\frac{1}{mN}\left(\leq\frac{1}{m^2} \right) $$ である。
ちなみに、この主張は、原点を通り傾きが\(a\)の直線\(y=ax\)に「いくらでも近い」整数座標を持つ点が存在することを意味しています。
既約分数\(\displaystyle\frac{n}{m}\)の小数点会は、ある桁から循環する。また、小数点以下\(k\)桁目で初めて循環が始まるとき、\(k\leq m\)である。さらに、循環部分の長さは高々\(m-1\)である。
今回はここまでです。
感想など是非コメントで教えて下さい!
結
今回は、「正八面体群は4次対称群群と同型である」ということを証明しました。
使った知識としては、群作用、置換表現、交代群です。
ちなみに、4次対称群は4次の置換の集合ですので、この主張は平たく言えば「正八面体の頂点は回転や対称を駆使すればどの点にも移ることができる」ということになります。
次回は正二十面体群が5次の交代群と同型であることの証明の一部を解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。





コメントをする