本記事の内容
本記事は、第二同型定理の証明をする記事です。
本記事を読むにあたり、正規部分群、商群(剰余群)、準同型定理(第一同型定理)について知っている必要があるため、以下の記事も合わせて御覧ください。
↓正規部分群の記事
↓商群(剰余群)の記事
↓準同型定理の記事
準同型写像の軽い復習
準同型写像
2つの群\(G_1\)、\(G_2\)の間の写像\(\phi:G_1\longrightarrow G_2\)は、群の構造を保つとき、すなわち- 任意の\(g,h\in G_1\)に対して\(\phi(gh)=\phi(g)\phi(h)\)である。
- 任意の\(g\in G_1\)に対して\(\phi(g^{-1})=\phi(g)^{-1}\)である。
- \(\phi(1_{G_1})=1_{G_2}\)である。
詳しくは、【代数学の基礎シリーズ】群論編 その5を御覧ください。
第二同型定理の明示
まずは、第二同型定理の主張を明示します。
定理0.(第二同型定理)
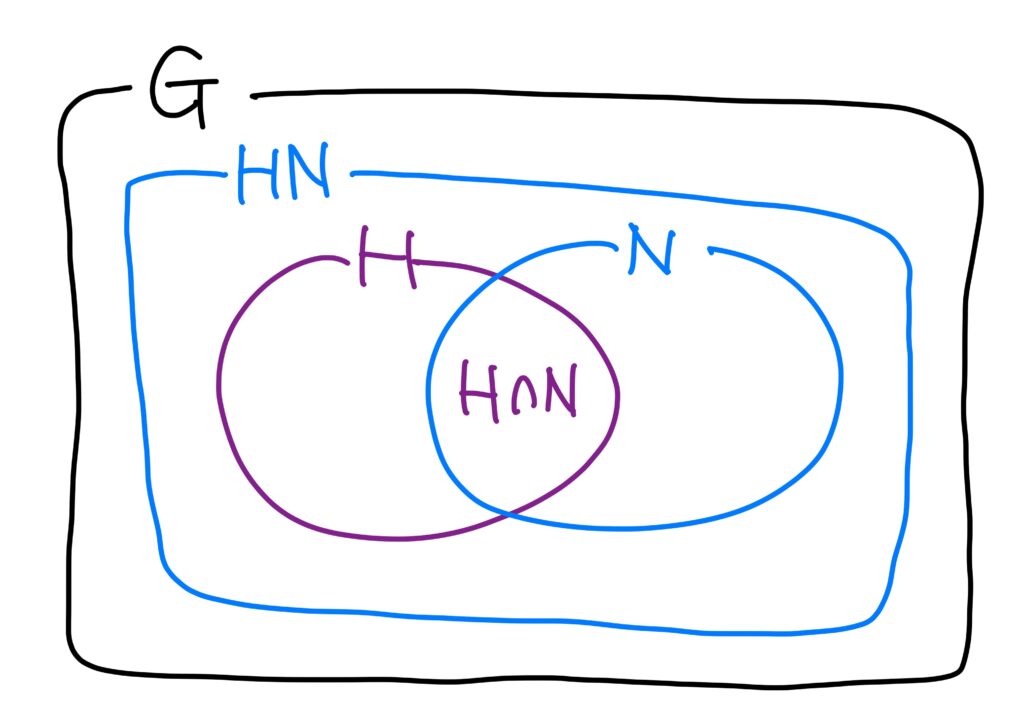
\(H,N\)を群\(G\)の部分群で\(N\triangleleft G\)、すなわち\(N\)は\(G\)の正規部分群とする。このとき、以下の2つが成り立つ。- \(HN\)は\(G\)の部分群である。また、\(HN=NH\)である。 ただし、 $$ HN=\left\{hn\middle|h\in H,\ n\in N\right\} $$ である。
- \(H\cap N\triangleleft H\)、\(HN/{N}\cong H/{H\cap N}\)である。
第二同型定理の証明
では、証明に入っていきます。
第二同型定理の証明
(1)の証明
まず、\(HN\)が\(G\)の部分群であることを示します。
このために、以下の事実を使います。
定理1.(部分群であることの必要十分条件)
群\(G\)の部分集合\(H\)が\(G\)の部分群になるための必要十分条件は次の3つの条件が満たされることである。- \(1_G\in H\)である。ただし、\(1_G\)は群\(G\)の単位元である。
- \(x,y\in H\Rightarrow xy\in H\)である。
- \(x\in H\Rightarrow x^{-1}\in H\)である。
定理1.の証明は【代数学の基礎シリーズ】群論編 その2を御覧ください。
- \(1_G\in H,N\)なので、\(1_G1_G\in HN\)です。
- 次の事実を使います。
この命題の証明は【代数学の基礎シリーズ】群論編 その4を御覧ください。
命題2.により、 $$ \left( h_1n_1\right)\left( h2n2\right)\in h_1Nh_2 N=h_1h_2 NN\subset HN $$ となるので、\(HN\)は結合律を満たします。 - \(h\in H\)、\(n\in N\)なら、 $$ \left( hn\right)^{-1}=n^{-1}h^{-1}\in Nh=hN\subset HN $$ となるので、逆元が存在します。
従って、定理1.から\(HN\)は\(G\)の部分群です。
\(h\in H\)なら\(hN=Nh\)なので、\(HN=NH\)です。
(2)の証明
\(H\)から\(HN/{N}\)への自然な写像は全射準同型で、その核は\(H\cap N\)です。
ここで準同型定理(第一同型定理)を使います。
定理3.(準同型定理(第一同型定理))
\(\varphi:G\longrightarrow H\)を群の準同型とする。\(\pi:G\longrightarrow G/{{\rm Ker}(\varphi)}\)を自然な準同型写像とするとき、以下の図が可換図式となるような準同型写像\(\psi:G/{{\rm Ker}(\varphi)}\longrightarrow H\)が唯一つ存在し、\(\psi\)は\(G/{{\rm Ker}(\varphi)}\)から\({\rm Image}(\varphi)\)への同型となる。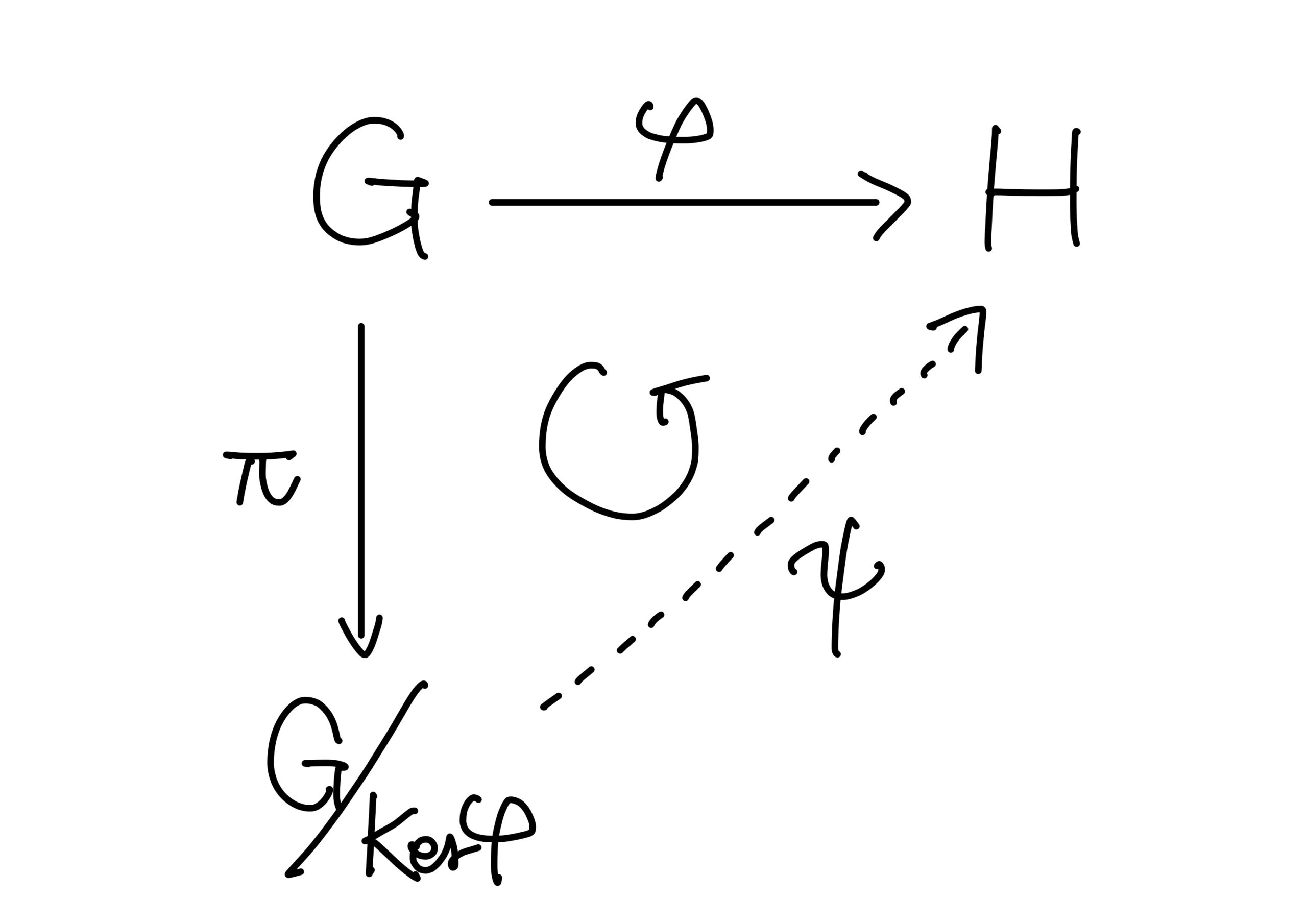
定理3.の証明は【代数学の基礎シリーズ】群論編 その5を御覧ください。
故に、\(H\cap N\triangleleft H\)であり、準同型定理(第一同型定理)から\(H/{H\cap N}\cong HN/{N}\)となります。
第二同型定理の証明終わり
第二同型定理のイメージ
第二同型定理のイメージ、特に第二同型定理の(2)のイメージを図を用いて言及します。
まず、\(H\cup N\subset HN\)です。
実際、\(H=H1_G\)、\(N=1_GN\)となるので、\(H\subset HN\)かつ\(N\subset HN\)なので、\(HN\)は\(H\)よりも広く\(N\)よりも広い集合だからです。

\(HN/{N}\cong H/{H\cap N}\)を図で描けば次です。
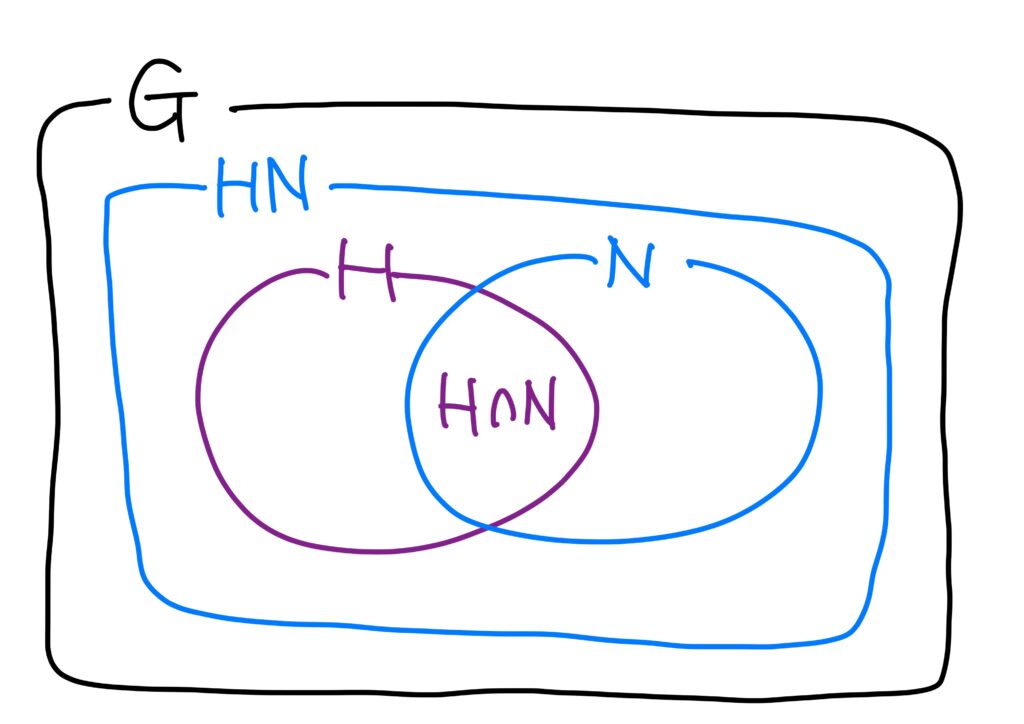
要するに、\(HN/{N}\)と\(H/{H\cap N}\)は群として本質的に同じものだ、ということが第二同型定理の主張です。
イメージとしては、\(HN\)の\(N\)に対する商群という広い集合と、\(H\)の\(N\)に対する商群という狭い集合が群として本質的に同じなので、より狭い範囲で考えることが出来る、ということがメリットです。
極端な(と言うより乱暴な)言い方をすれば、「群においては(条件はあれど)大きいモノを大きなモノで割った商と小さいモノを小さいモノで割った商が本質的に同じ」ということです。
皆様のコメントを下さい!
今回はアラン・チューリングです。
アラン・チューリング(Alan Mathison Turing、1912年6月23日–1954年6月7日) イギリス出身の数学、論理学者、暗号解読者、計算機科学者であり、今日チューリングマシンとよばれる計算機の理論的モデルを用いて「アルゴリズム」と「計算」の概念を定式化しました。
この研究は計算機科学の発展に大きな影響を及ぼし、またコンピュータの誕生に重要な役割を果たしました。
このことから計算機科学および人工知能の父と言われています。
第二次世界大戦中は、ドイツの暗号解読に携わり、ドイツ海軍のU ボートの暗号通信を解読する部門の責任者となりました。
ドイツの暗号機エニグマの設定を見つけるための機械bombeを開発しました。
1952年、同性愛の罪で逮捕され、保護観察中にホルモン療法を受けます。
1954年、42歳の若さで死去。
検死により、青酸中毒による自殺と断定されました。
如何でしたか?
今まさにこのブログを読んでくださっている方が手に持っているスマホ、パソコンの核の部分の理論を作った方です。
ここに書かれている事のほかにでアラン・チューリングについてご存知のことがあれば是非コメントで教えて下さい!
結
今回は第二同型定理の証明を解説しました。
準同型定理は、群論において最も重要と言っても過言ではないほどの定理です。
実際、群論の講義のゴールとして準同型定理を挙げていたりします。
第二同型定理は、平たくいえば、広い商群と狭い商群が同型だ、という定理です。
次回は第三同型定理について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
代数についてより詳しく知りたい方は以下を参考にすると良いと思います!






コメントをする
(2)の証明の一行目の文章でおそらく「核」の変換が間違って「角」となっているのではないでしょうか。
名無し様
コメントありがとうございます。
>(2)の証明の一行目の文章でおそらく「核」の変換が間違って「角」となっているのではないでしょうか。
とのお問い合わせですが、おっしゃるとおり誤字でございました。訂正いたしました。
ご指摘ありがとうございました。