(数セミ)”エレガントな解答をもとむ”に1時間で挑戦！【1時間チャンジシリーズ】挑戦②

本記事の内容

本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。

本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。

今回は「エレガントな解答をもとむ selections」に掲載されいている問題です。

問題①

今回はパズルの問題です。

図は引用部分の下にまとめて表示します。

パズル(初級)
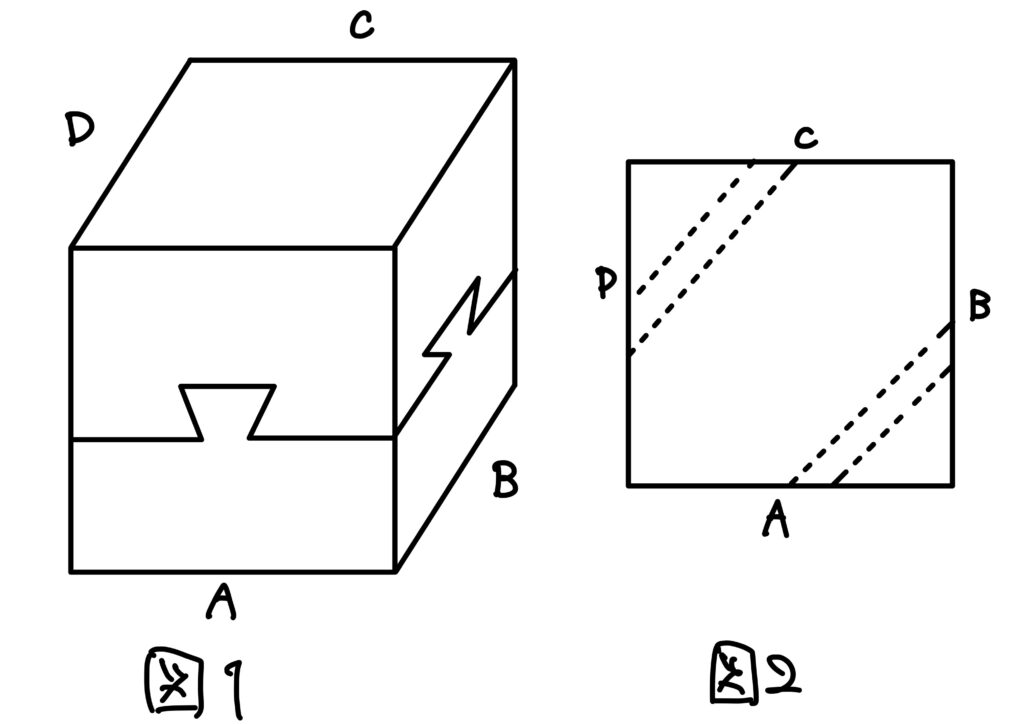
２つの木片を組み合わせて図１の立体を作って下さい。立体の側面は$A=B=C=D$とします。もちろん立体は中空部分をもたず、また自由に２つの木片に分解できなければなりません。
さて、このパズルの答は図２のとおりです。
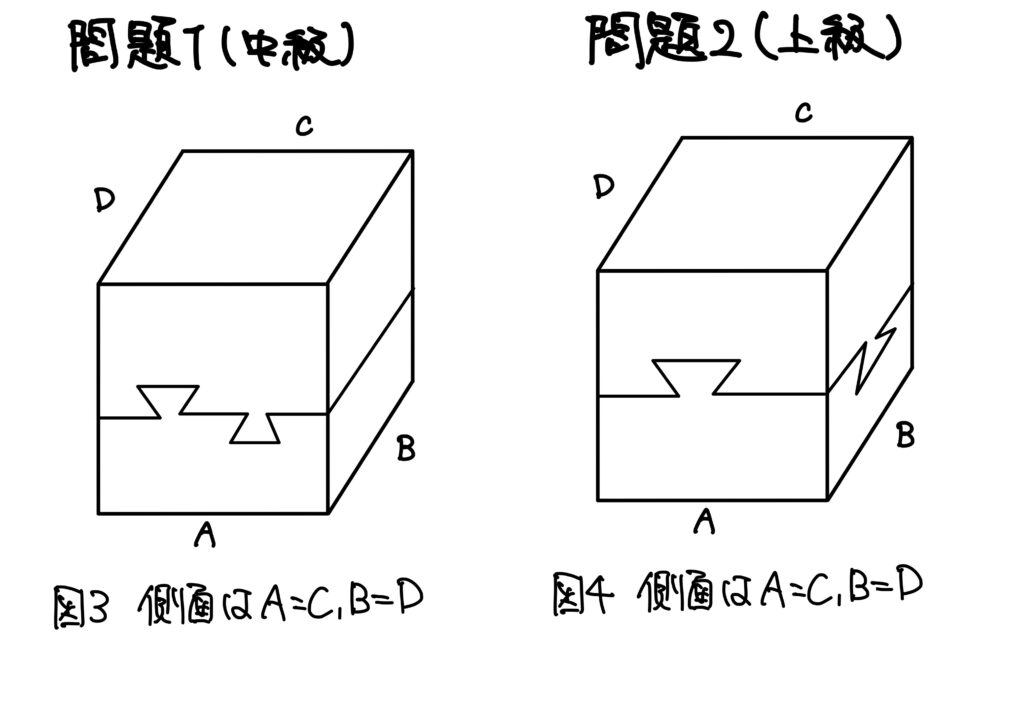
それでは以下の立体はどうでしょうか？(問題２はむずかしいと思いますので、問題１だけでも挑戦して下さい。)

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p6-p7.

いざ、チャレンジ①

チャレンジの結果….問題１はできましたが、問題２は解けませんでした…..

問題１は力技で「これはエレガントなのだろうか？」という感じになってしまいましたし、問題２に至っては時間制限と格闘して結果的にダメでした。

以下に筆者が考えたことをそのまま書きます。

筆者の解答

「スライドして組み合わせるんでしょ？」ということにはすぐ気が付きました。
なぜなら凹凸の形状から真上からかぶせてジョイントすることは不可能だからです。

問題1について

筆者は最初、「問題１？楽勝じゃん。一瞬だよ。」と思いました。
なぜなら以下のようにすれば直ちに解決だと思ったからです。

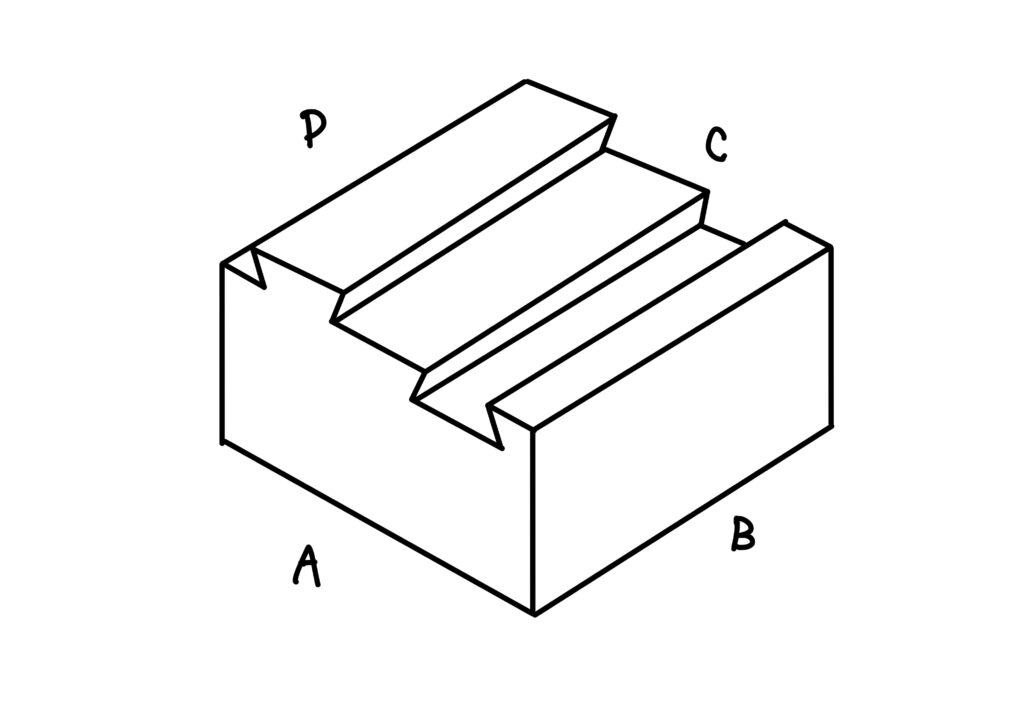
実はこれは間違いです。
なぜかと言うと、仮定$A=C$かつ$B=D$を満たしていないからです。

先程の筆者の解答だと、面$A$と面$C$一致せず、互いに鏡像の関係になってしまいます。

さて、どうしたものかと。

「マズいぞ…問題１は簡単です、みたいな言い方をしていたのに…できない…」と思いましたがここで、ふと思いつきました。

それは「真横からのスライドでジョイントができなさそうなら、斜めからスライドする方法だってあるじゃんね？」ということです。

次にこの方針で考えてみました。
斜めからスライドする方法でジョイントするのだから、「飛び出ている部分から凹んでいる部分にかけて傾斜している必要があるな？」と思い、以下を思いつきました。

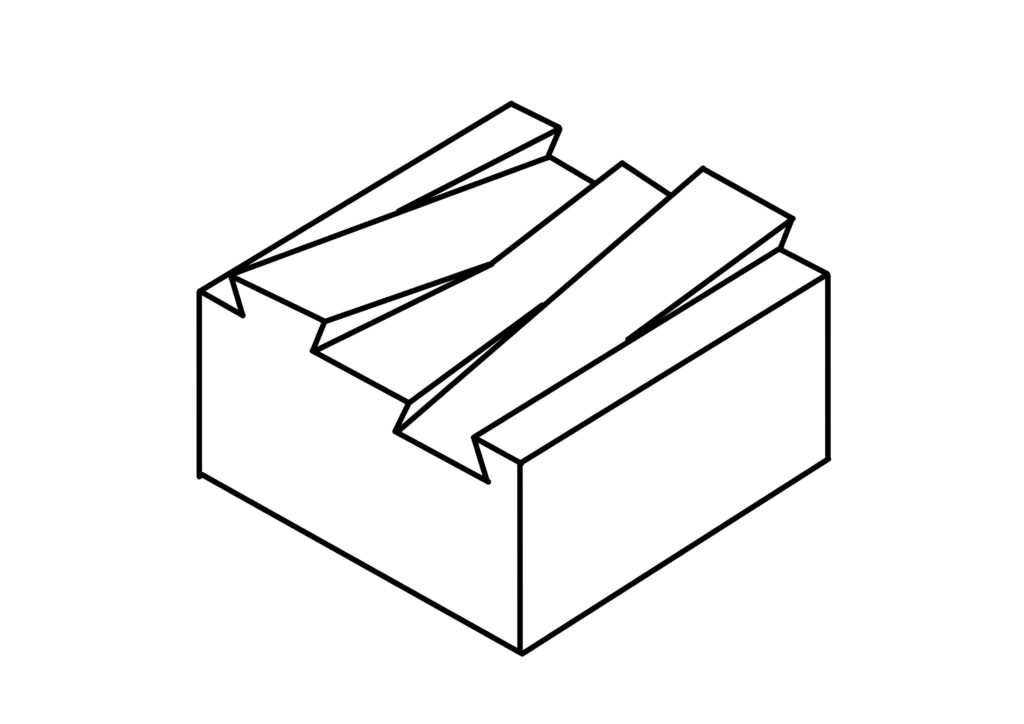
でもやっぱりダメでした。
ジョイントできません。
片側だけだったら、お終いだったのですけれど….

ここでヤケになりました。
「一方の飛び出てる部分を固定してろうじゃないか」と。

そしたらなんと、できました。
それが以下です。

問題2について

問題2に入る段階で既に45分が経過していて、あと15分しか有りませんでした…(言い訳)

でも、もしかしたら筆者の頭が冴えに冴えて1秒とかからず解けるかもしれません。
ということで挑戦してみましたが…..

案の定冴えに冴えるということはなく、解けませんでした。
「ナンジャコレ？」状態でした。

「もしかして問題1と同じようにできるのでは？」とは思ったのですが、それを確認している途中で時間切れでした。

投稿されたエレガントな解答とその感想①

問題１

出題者は複数の解答を提示していますが、筆者と一致しているものもあったので、それについては省略します。
とはいえ、解けたことは嬉しいのですが、出題者は自分とは異なる解答を求めていると思うと少々残念です。

問題1の解(回転) 図９のように軸$O$を中心として回転すれば分解できます。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p40.

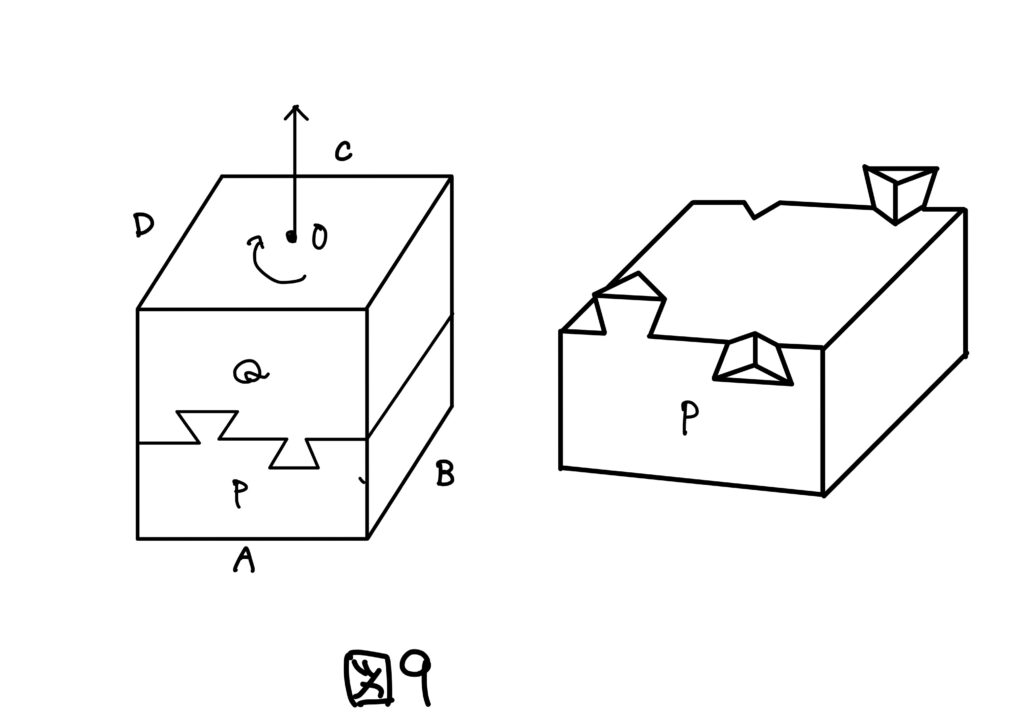
“回転”でもってジョイントする、という発想は筆者には有りませんでした…すごい…

問題２

さてさて、気になるのは問題２です。
どうやら、平行移動を駆使した解答と回転を駆使した解答があるようです。

問題２の解(平行移動) 図７に示すように、木片$Q$をベクトル$\beta$の方向へ平行移動することで２つの木片に分解します。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p39.

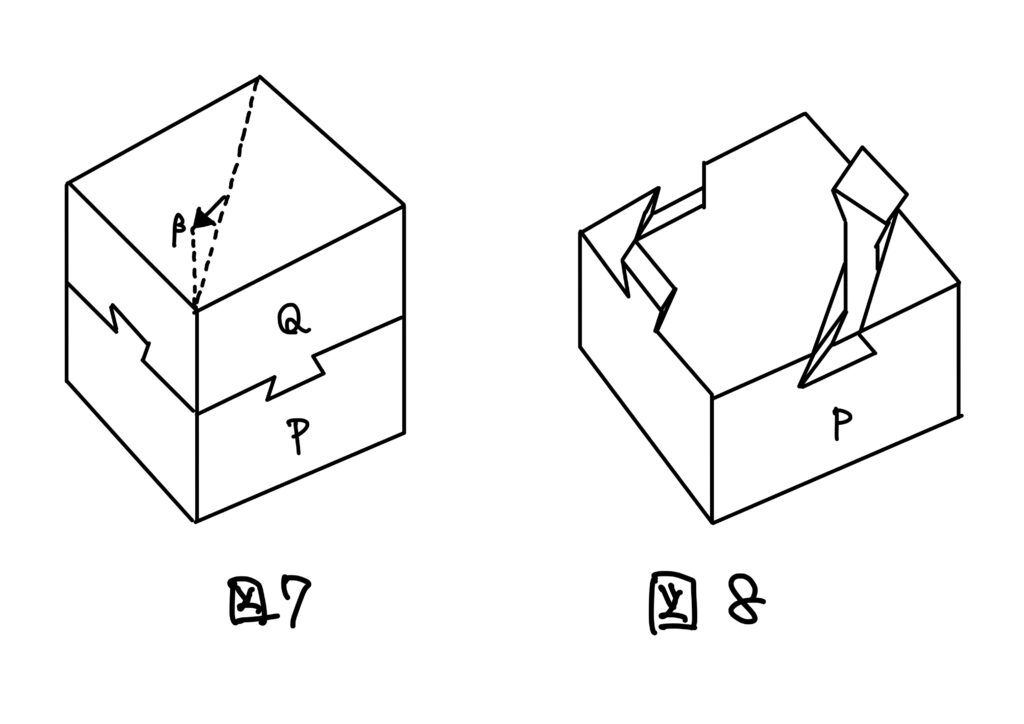
すごいですね…どうやって導き出したのか気になります….

問題２の解(回転) 図10のように軸$O$を中心に回転させながら情報へ分解します。また、回転軸$O$を中心ではなく隅にとった解答もよせられました。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p42.

世の中には凄い方がいらっしゃるものですね…
“回転を使う”という発想は筆者には一切ありませんでした….

回転を使う方が立体としても回転対称性があってキレイですし…すごいなあ…

ちなみに、筆者が確かめ損なった解答は掲載されていないことから恐らく不正解なのでしょう。
もしかしたら「エレガントでない」という理由で排除されているのかもしれませんが。
いずれもいずれ、筆者の頭では敵いませんでした。

問題②

今度は毛色が変わって数の問題です。

1から9までの数字を一個ずつ用い、これと山陽記号を組み合わせて指定された数を表すパズルを、小町算と呼んでいます。
今回その小町算に挑戦することとし、2の平方根(言うまでもなく、約1.41421356)の近似値を表して下さい。
使用できる記号は加減乗除($+,\ -,\ \times, \div$)と小数点、かっこ、階乗(!、例：$3!=3\times2\times1=6$)とし、根号の使用やベキは認めない。0.2を.2で表すことは許されるとします。むろん、より近似した解が望ましいが、ねらいの面白い解やスマートな解も「エレガント」であるとします。
解答には式だけでなく、そのねらいや思いついた経緯等も書き添えていただきたい。見本には解答例を載せておきます。これらはあまり良い解とは言えませんが、あくまでもみほんであることをつけ加えておきます。
$$\begin{eqnarray} &&(5+6+8-9)\div (12-3\times4+7)=10\div7=1.428\cdots\\ &&.6243+.78951=1.41381 \end{eqnarray}$$

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p7.

いざ、チャレンジ②

まず先に言い訳をすると…筆者はこの手の問題が大の苦手です。
というより、四則演算が苦手です。

数学をやっているのにおかしな話ですが、実は(?)苦手です。
さらに言い訳をすると、数学をやっていると具体的な実数値に出くわすことはあまり少ない気がしています….

弱気になっているわけですが、もしかしたら筆者の頭が冴えに冴える場合だってやはりあるわけです。
先程は自分を信じて挑戦し、結果は伴いませんでしたが、今回はもしかしたら冴えるかもしれません。

さて、結果ですが…….「一応解けたがエレガントなのか？」です。
なんとまあ頼りない感じになってしまいました。

筆者の頭は冴えませんでした。
一体いつになったら冴えるんでしょうか、私の頭は。

筆者の解答

先程、この手の問題は苦手だ、と言い訳しました。
苦手なら苦手なりに力技でどうにかしてやろうと開き直りました。

まず、いきなりですが、加減乗除の記号、小数点、かっこ、階乗の全てを使うことは諦めました。
「随分弱腰だな」という感じですが、許して下さい。

さて、まず一番シンプルなのは、出題者が挙げた足し算による近似で、出題者よりも高精度のものを出す、ということだと感じました。
そこで、足し算により解答してみました。

まず、$\sqrt{2}=1.41421356\dots$を単純に2つの実数の和に直してみました。
$$1.41421356\dots=1+0.41424356\dots$$
これは1と4が複数回出現するため、直ちに間違いだと分かります。

さて、脳筋方針ですがとりあえず、以下の2パターンを考えました。

• 1を値として減らして0.41424356$\cdots$を値として増やす。
• 1を値として増やして0.41424356$\cdots$を値として減らす。

まずは1を値として減らすパターンで考えました。
とりあえず使える数字は9種類なので、その約半分の5個を使うことにしました。
$$0.98765-1.41421356=-0.42656356$$
となって、ダメでした。
(※「君、阿呆じゃないか？」と思っている方、分かります。今この記事を書いている筆者もそう思います。桁数を見なさいよ、という話ですよね。)

さらに繰り返してみます。
$$\begin{eqnarray} &&0.987654-1.41421356=-0.42655956\\ &&0.9876543-1.41421356=-0.42655926 \end{eqnarray}$$
ということでダメでした。
以降は0.4$\cdots$の形をしているため、不可能だということが分かりました。

では、今度はまた５桁だけ使って、数字の順番を変えてみました。
$$\begin{eqnarray} &&0.98756-1.41421356=-0.42665356\\ &&0.98576-1.41421356=-0.42845456\\ \end{eqnarray}$$

ここで、筆者は自分がアホなことをしていることに気が付きました。
桁数を考えてなかったからです。
最初に5つの数字を使っているので、もう５つの数字を使う必要があるのですが、単純に1.41424356を引く、という操作では8桁も出現するため、ダメです。

そこで、1.41421356ではなく、1.4142を目指すことにします。
「もういっかいやるのか…」と思いながら電卓を叩きます…

$$\begin{eqnarray} &&0.98765-1.4142=-0.42655\\ &&0.9876-1.4142=-0.4266\\ &&0.987-1.4142=-0.4272\\ \end{eqnarray}$$

「んー。うまくいかん。」ということで、1.4142ではなく１桁増やして1.41421にしてみました。

$$\begin{eqnarray} &&0.98765-1.41421=-0.42656\\ &&0.9876-1.41421=-0.42661\\ &&0.987-1.41421=-0.42721\\ \end{eqnarray}$$

「これでもいかんか」ということで、ここで方針を変えてみました。

$$\begin{eqnarray} &&0.98765+0.4321=1.41975\\ &&0.98765+0.4312=1.41885\\ &&0.98765+0.4231=1.41075\\ &&0.9876+0.54321=1.53081\\ &&0.987+0.654321=1.641321\\ &&0.987+0.436521=1.423521\\ &&0.987+0.436512=1.423512\\ &&0.987+0.436152=1.423152\\ &&0.987+0.436215=1.423215\\ \end{eqnarray}$$

ここで「ん？似てきたか？」となりました。
そこで、ぐっと睨んだときに「もしかして、0.987じゃなくて0.978だったら近づきそうじゃない？」と予想して計算してみると、
$$0.978+0.436215=1.414215$$
となりました。

「うおおおおおおお」と声が出ました。
全然スマートじゃないし、完全に脳筋のちから技ですが、出題者が提示したものよりも高精度で出すことができました。

本記事に書いていないパターンもいっぱい計算しました。
ここで55分。疲れたのでやめました。

投稿されたエレガントな解答とその感想②

（前略）
筆者の予想9桁を軽く超えてなんと11桁合っている。式の表し方は、解答のままとした。
①$(3-.1)\times\{2-4\div(8!\div6+7)\}\div(5-.9)=\underline{1.4142135623}8$
②$\displaystyle\frac{.9\times(5+6)}{\displaystyle7+\frac{3!\times2.4}{8!+1}}=\underline{1.4142135623}2$

①の方はもうわずかのところで、12桁合致するところであった。

（中略）

（１）加減算
（中略）
④$.8+.6142+5\div\{9!+7!+(3!)!\}=\underline{1.41421356}\cdots$

（中略）

（３）ニュートンの近似式
（中略）
78404/55440(=19601/13860)を得ている。

（中略）

次にねらいの面白い書いやスマートな書いをいくつか紹介しよう。まず$A\div B$型の単純な解。それでいて近似度も結構高い。
（中略）
⑤$12653\div8947=\underline{1.41421}7\cdots$
⑥$3517\div2486.9=\underline{1.41421}0\cdots$
（中略）
⑦$3\div7+.9856421=\underline{1.4142135}2\cdots$
（中略）
⑧$1+2\times3!\div\{4!+5-6!\times(7+8)\div9!\}=\underline{1.41421}82\cdots$
⑨$9\div(.8\times7)-6\div(5!\div4+3-2.1)=\underline{1.41421}68\cdots$

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p44-p47.

どれも凄いですね…投稿者の皆様はラマヌジャンみたいな方ですね…
なんでこんなのを思いつくんでしょうか。

引用では省きましたが、連分数展開を使った方もいたようです。
確かに、その手があったか、と思いました。
またニュートンの近似式については、数値計算を学習している方なら直ちに思いつくのかもしれないなと思いました。

個人的に⑧と⑨がエレガントだな、と思いました。
とてもキレイだと思います。
これを思いつくのは本当に凄いと思います。

結

いかがでしたか？
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
実際に紹介されている解答は確かに”エレガント”だな、と思いました。

読者の皆様も是非一度挑戦してみて下さい！
そして、「こんな解答を思いついた！」というのがあれば是非コメントで教えて下さい！

質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

Twitterでもリプ、DM問わず質問、コメントを大募集しております！