本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
では、問題
円\(O\)の内部に円\(O^\prime\)があります。そして、\(O\)に内接し、\(O^\prime\)に外接する三角形\(ABC\)があるとします。(このような三角形を、\(O-O^\prime\)内接外接三角形と呼ぶことにしましょう。) このとき、円周\(O\)上の任意の一点\(P\)に対し、\(P\)を一頂点とする\(O-O^\prime\)内接外接三角形が存在することを示して下さい(図1)。さらに一般に、内接外接(星形)多角形についても同様のことが成立するかどうか調べてみて下さい(図2)。エレガントな解答を期待していますが、、えれー頑固な解答でも結構です。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p15.
いざ、チャレンジ
チャレンジの結果、\(\displaystyle\frac{1}{4}\)だけ解けた(点数で言えば25点)というなんともお粗末な話でした。
問題文を注意深く見れば、少なくとも半分は取れていました。
負け惜しみですが…
恥ずかしいお話
オイラーの定理(後で明示します)を見つけて、「あれ?これでできるんじゃん?」と思い「なーんだ。20分くらいで半分解けちゃった。」と思い上がっていましたが、後に示すように、逆を示すことを忘れていました….
「問題文をよく読もうね」ということと「何を示さなければならないのかをしっかり確認しようね」と改めて自分に言い聞かせることになりました。
これは、数学をやる上で(数学だけではないかも知れませんが)最も基本的なことだと思いますので、なんとも恥ずかしい話です。
筆者の回答
この問題を見た瞬間、図1については円\(O\)と\(O^\prime\)が同心円であれば、証明するまでもなく正しい、ということはわかりました。
なぜなら、円の中心で回転すれば、点\(A,B,C\)は円\(O\)の円周上を動くからです。
故に、\(O\)と\(O^\prime\)は同心円でない場合を考えることにしました。
ここで数分問題を睨んだところ、「そういえば、確か同じような状況で\(O\)と\(O^\prime\)の半径の間にある関係式があった気がする。」と思い調べてみました。
最も、”気がするだけ”ですし、最初は「同じような状況の図を見たことがある気がする」程度でしたが。
そこで調べたところ、オイラーの公式(またオイラーだ)というものを見つけ(というより思い出し)ました。
定理0.(オイラー)
内接円の半径を\(r\)、外接円の半径を\(R\)とするとき、外心\(O\)と内心\(I\)との距離\(d\)は次で表される。 $$ d^2=R^2-2Rr $$この定理の証明は、後述するエレガントな解答の中で述べます。
このオイラーの定理が言うには、「\(d^2=R^2-2Rr\)という関係式は内接外接三角形のいちには依存しない。」ということです。
すこし丁寧に言うと、「内接外接三角形がどこにあろうとも、その場所に関係なく\(R\)、\(r\)、\(d\)の間には\(d^2=R^2-2Rr\)という関係式がある。」ということですので、そのまま今回の問題に適用できます。
しかし、恥ずかしいお話でも述べたとおり、これだけでは証明として不十分です。
後は、任意の位置に内接外接三角形が存在することを示す必要がありました。
それを失念していました。
とはいえ、結局定理0.を注意深く逆にたどれば良いわけですので、さほど難しくはありません。
ただ、難しくはないけれどもその操作を忘れていた、というのはなんとも情けなくお粗末なお話です。
さて、前半の証明は終わった(と思っていたに過ぎないのですが)ということで、後半の証明に取り掛かりました。
定理0.と同様なことが星型でも成り立つのではないか?と定理0.の証明を追いながら考えてみましたが、特に何かを見つけることはできませんでした。
ここで時間切れです。
投稿されたエレガントな解答
(前略)
いただいた答案で、正解に淘汰圧しているものは、おもに次のように分類されます。
(1)チャペル(Chappel)の式を証明し、それを用いる。
(2)\(O^\prime\)に関する反転を用いる。
(3)\(O^\prime\)に接しながら、\(O\)の弦を動かしたときの、両端の速さの比を用いる。
(4)その他の初等幾何的解法。(1)の方法でチャペルの式とは、「\(O-O^\prime\)内接外接三角形が存在するとき、円\(O\)の半径を\(R\)、円\(O^\prime\)の半径\(r\)、2円の中心間の距離\(d\)の間には、\(d^2=R^2-2Rr\)が成立する」というものです。証明の代表的なものを、一つあげておきます。
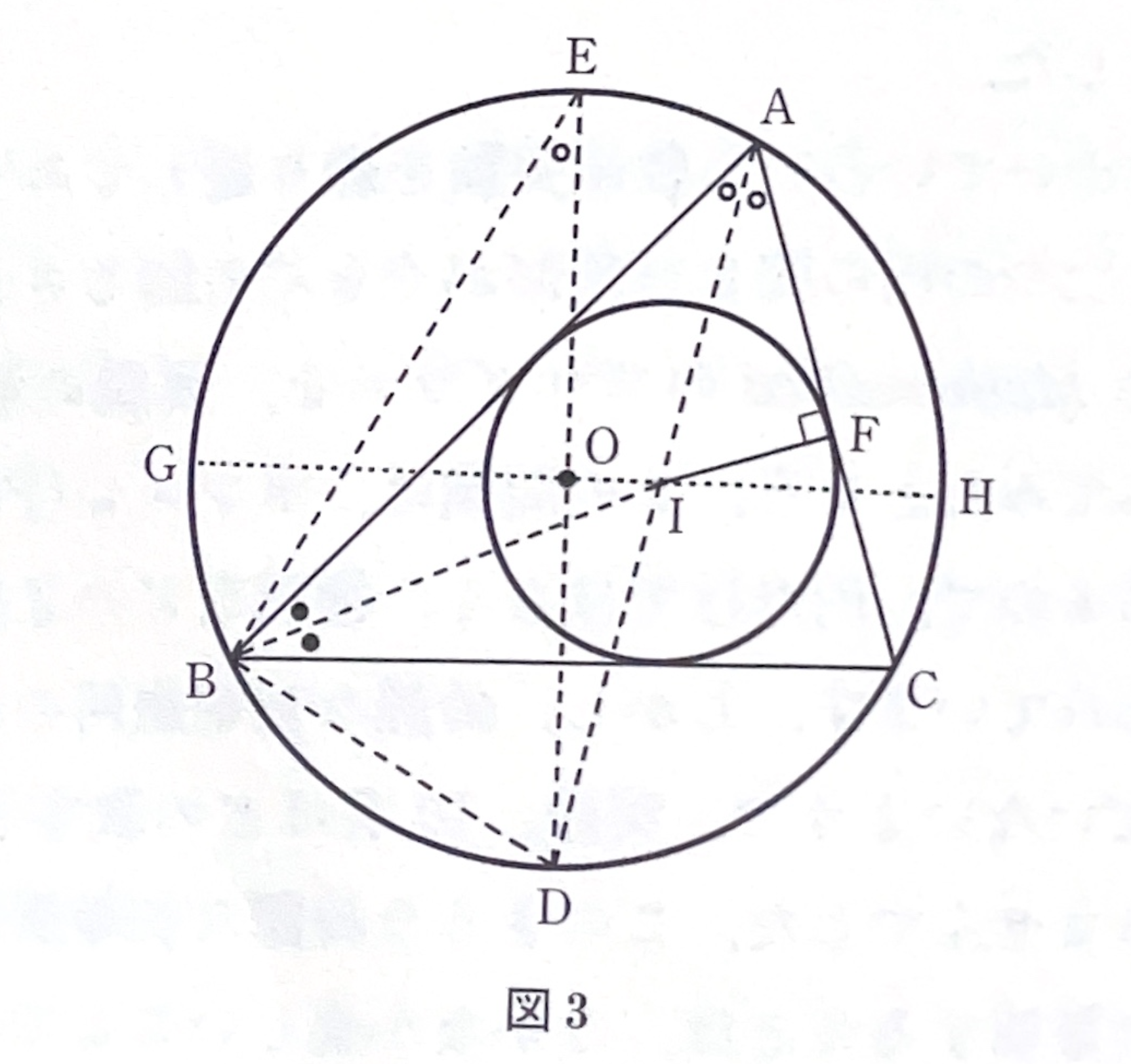
図3のように補助線を引きます。ここで、\(O,I\)は円\(O,O^\prime\)の中心で、\(DE,GH\)は直径とします。\(\angle IAF=\angle DEB\)より、\(\triangle AIF\unicode[serif]{x223D}\triangle BDE\)。したがって\(2Rr=DB\cdot AI\)。また、
\begin{eqnarray}
\angle DBI&=&\angle DBC+\angle CBI=\angle DAC+\angle CBI\\
&=&\angle ABI+\angle BAI=\angle DIB
\end{eqnarray}
より、\(DB=DI\)。方ベキの定理より\(DI\cdot AI=GI\cdot HI\)。したがって、
\begin{eqnarray}
2Rr&=&DB\cdot AI=DI\cdot AI=GI\cdot HI\\
&=&(R+d)(R-d)=R^2-d^2.
\end{eqnarray}
チャペルの式は、内接外接三角形がどこにあろうとも、その場所に関わらず、\(R,r,d\)の間には、決まった関係があることを示しているのですが、これだけれは問題の証明には不十分で、あと、任意の位置に内接外接三角形があることを示す必要があります。そのためには、上の照明の逆を注意深くたどればよいので、ここでは省略します。この「逆を示す」ことを忘れている方が数人いましたが、大目に見ました。また、この方法では、後半の証明に拡張することは無理なようです。
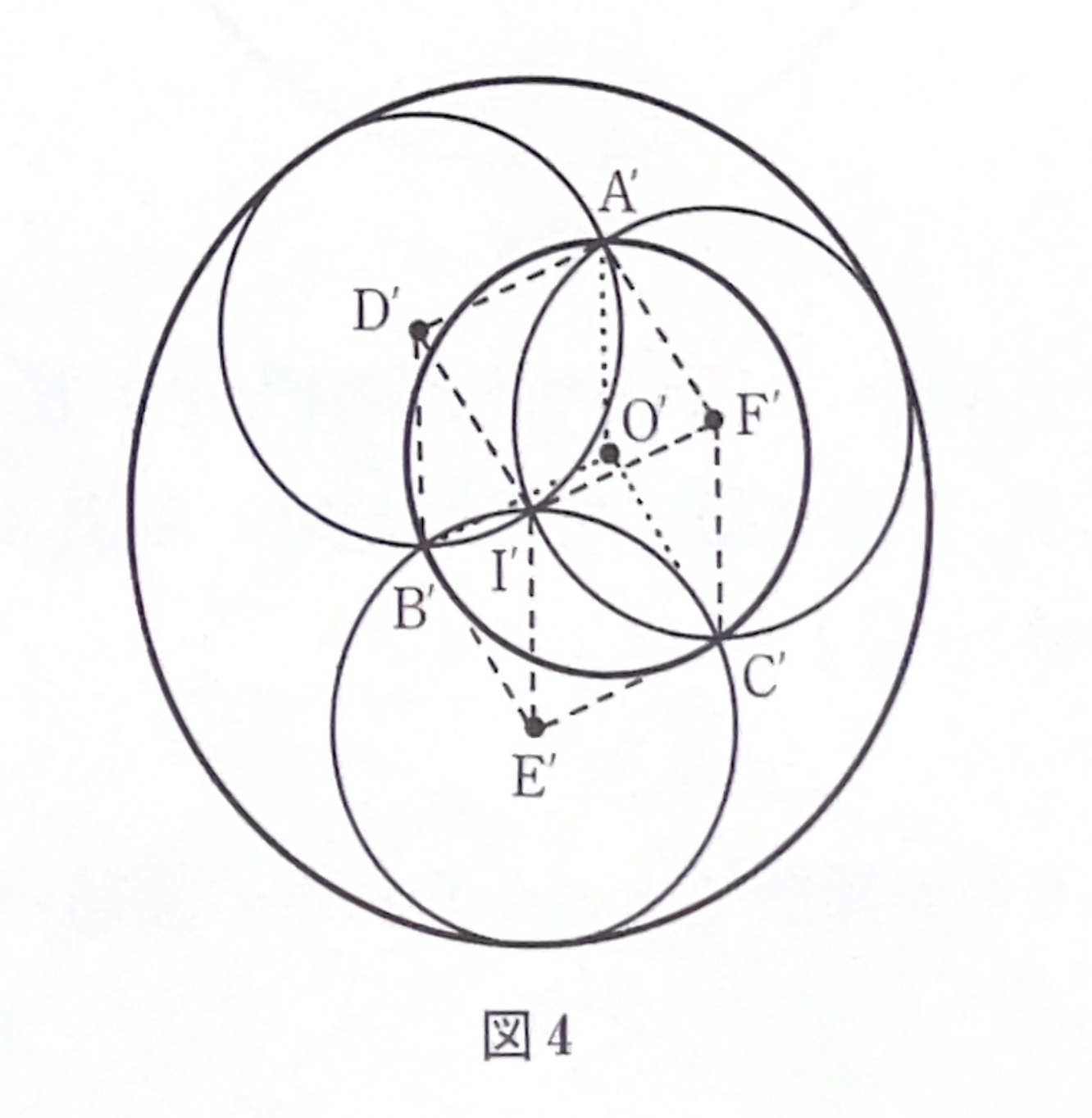
(2)の方法では、(中略)の2名の方が解答をされていました。反転について、簡単に説明します。\(O\)を原点中心の半径\(a\)の円とします。平面上の点\((r\cos\theta,r\sin\theta)\)を点\((a^2/r\cos\theta,a^2/r\sin\theta)\)に移す変換を円\(O\)での反転といいます。ただし、原点は無限遠点に移されるものとします。反転によって、平面上の任意の円または直線は、円または直線に移されます。さて問題の証明ですが、ここでは、(中略)の解答を紹介しましょう。記号の簡約のため、内側の円\(O^\prime\)を円\(I\)と記すことにし、円\(O\)を反転した円を\(O^\prime\)と記すことにします。また、反転前の記号に\({}^\prime\)をつけることにより、反転後の対象物を表すことにします。
円\(I\)で反転を行うと、直線\(AB,BC,CA\)は全て、円\(I^\prime\)の中心を通り\(I^\prime\)に接する3つの円になります。円\(I^\prime\)の半径を\(2r\)とすると、これら3円の半径は\(r\)となります。これらの円の中心を\(D^\prime,E^\prime,F^\prime\)とします。\(A^\prime D^\prime B^\prime E^\prime C^\prime F^\prime\)は図4のように等辺平行6角形を成します。円\(O^\prime\)は\(A^\prime,B^\prime,C^\prime\)を通るので、その半径は\(r\)であることがわかります。また、\(P\)から円\(I\)に引いた接線が円\(O\)と交わる点を\(Q,R\)とすると、直線\(PQ,PR\)を反転した結果は、円\(I^\prime\)の中心を通り\(I^\prime\)に接する半径\(r\)の円になり、直
線\(QR\)は\(Q^\prime,R^\prime\)および円\(I^\prime\)の中心を通る円になります。これらの円を\(S^\prime,T^\prime,U^\prime\)とします。ここで、\(P^\prime,Q^\prime,R^\prime\)は円\(O^\prime\)上にあることから、少しの考察により、円\(U^\prime\)の半径は\(r\)であることがわかります。したがって円\(U^\prime\)は円\(I^\prime\)に接し、よって直線\(QR\)は円\(I\)に接します。
(中略)
(3)の方法は、じつは私自身の回答として準備していたのは、この方法でした。(中略)
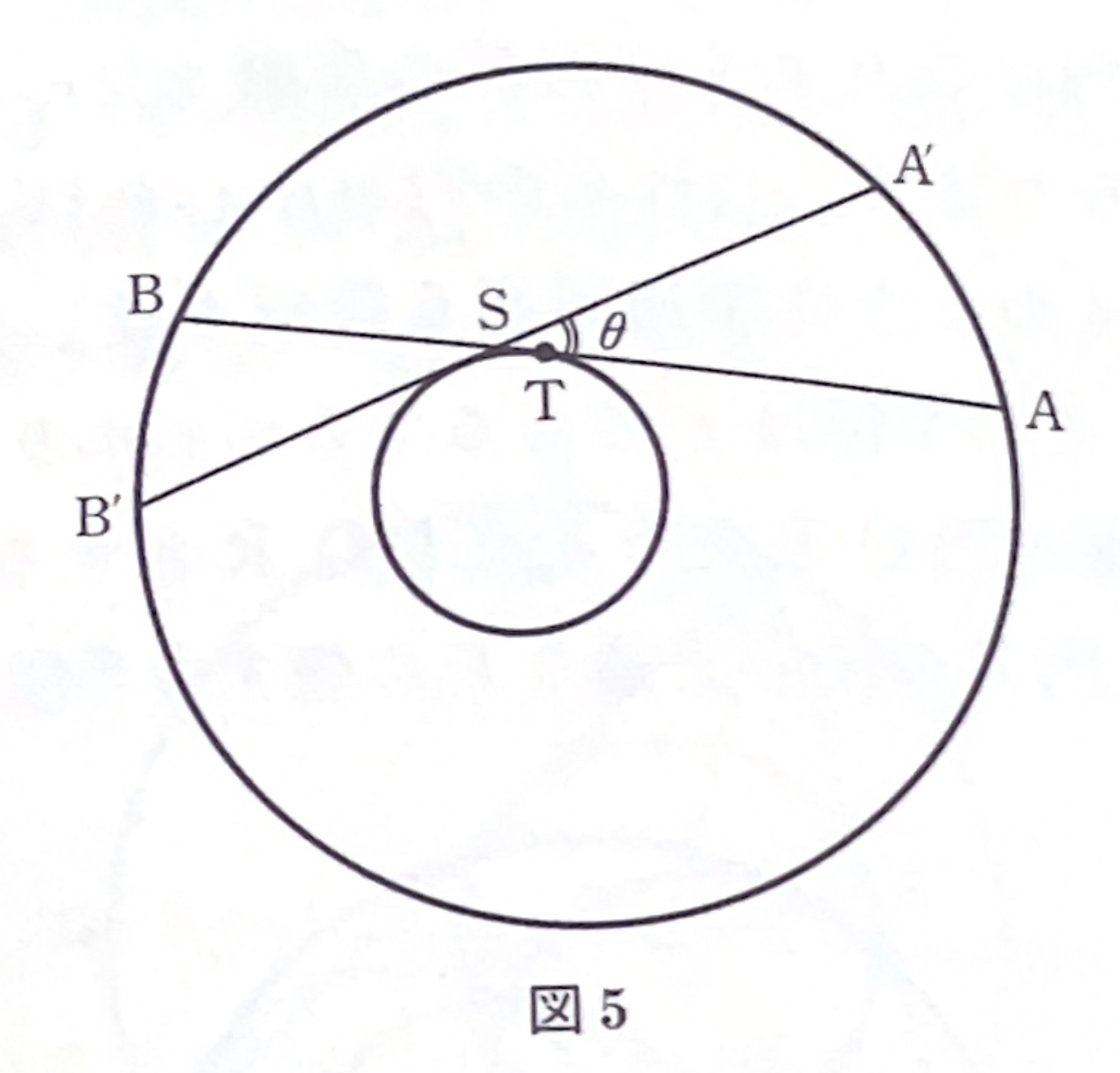
図5において、\(\theta\to0\)として、弦\(A^\prime B^\prime\)を弦\(AB\)に近づけると、
$$
\frac{AT}{A^\prime S}\to1,\quad \frac{BT}{B^\prime S}\to1,\quad \frac{\stackrel{\huge\frown}{AA^\prime}}{AA^\prime}\to1,\quad \frac{\stackrel{\huge\frown}{BB^\prime}}{BB^\prime}\to1
$$
であるから、\(\displaystyle\frac{\stackrel{\huge\frown}{BB^\prime}}{\stackrel{\huge\frown}{AA^\prime}}\to \frac{BT}{AT}\)となります。よって、次の補題が得られました。
補題 「円\(O\)の弦\(AB\)が、円\(O\)の内部の円\(O^\prime\)に接しながら動くとき、ある瞬間における\(A\)と\(B\)の動く速さの比は、\(A,B\)から円\(O^\prime\)に引いた接線の長さの比に等しい。」
速さを積分したものが場所であるから、この補題の逆も成り立ち、次の命題を得ます。
命題 「\(O-O^\prime\)内接外接多角形が与えられたとき、全ての頂点を、その頂点から\(O^\prime\)へ引いた接線の長さに比例した速さで動かせば、つねに全ての辺が円\(O^\prime\)に接していることになる。」
この速さを積分したものが、第1種の楕円積分の一つなのですが、ここでの証明には、その知識はまったく必要ありません。また、この証明は、そのまま後半の証明にもなっています。
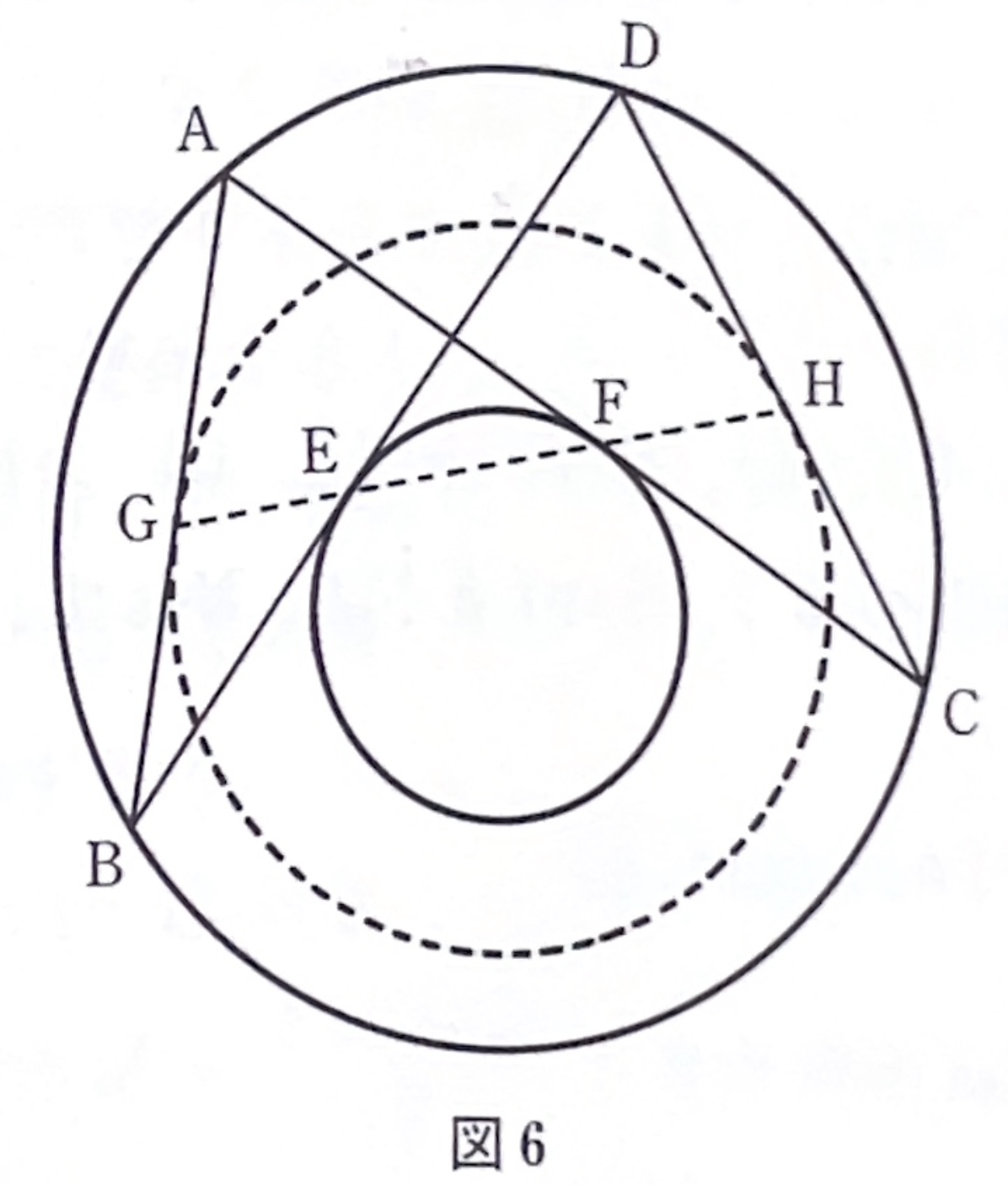
(4)の方法、すなわち、以上3つの方法以外で正解に到達されていたのは、(中略)の2名の方でした。特に(中略)氏は「円\(O\)に内接する四角形\(ABCD\)の対角線\(BD\)と\(AC\)とが、他の円\(O^\prime\)に接する点を\(E,F\)とし、\(EF\)が\(AB,CD\)と交わる点を\(G,H\)とすれば、\(AB,CD\)と\(G,H\)で接し、\(O,O^\prime\)と共軸な円が存在する(図6)」という補題を用いて、問題の後半部分を、初等幾何の範囲で見事に証明されていました。(中略)氏の証明は、前半部分だけではありますが、独特なものでした。ここで、紹介できないのが残念です。
なお、「円\(O,O^\prime\)を反転によって、同心円にする」という方法で、3名の方が解答されていましたが、同心円の中心が反転の原点と一致すると勘違いされていたため、残念ながら正解に至っておりません。
エレガントな解答だと私が独断で判断したものは、年齢とその自由な発想から、(中略)さんと(中略)さんのものです。また、(中略)氏の解答は、「初等幾何をあまり勉強していない私には、できそうにない」という意味で、えれー頑固な解答だと思いました。そして、残念ながら、正解に至ってはいなかったものの、9歳という年齢で挑戦してくれた(中略)君には今後の健闘を期待しています。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p107-p112
極限を使う、というのは「なるほど」と思いました。
幾何の問題で極限の話を使うという発想は確かにアリだと思います。
直線が直線に収束する、というのは関数列の極限ということで記述できるのでしょうが、その点難しいと思います。
読者の皆様への挑戦状!
今から紹介する問題の解答は来週の日曜日に解説します!
直角二等辺三角形をある方向に拡大すると再び直角二等辺三角形になったとします。何倍したのでしょうか。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p16.
もう少し正確にいうと次のようになります。\(xy\)平面上の直角二等辺三角形について、\(y\)座標はかえずに\(x\)座標を\(a\)倍(\(a\)は\(1\)より大きい実数)したとき、この三角形が再び直角二等辺三角形になったとします。このときの\(a\)の値を求めて下さい。もちろん\(x\)軸と\(y\)軸は直交しているとします。
前回の問題は【1時間チャレンジシリーズ】挑戦⑬を御覧ください。
結
いかがでしたか?
今回も数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!





コメントをする