本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回は「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
では、問題
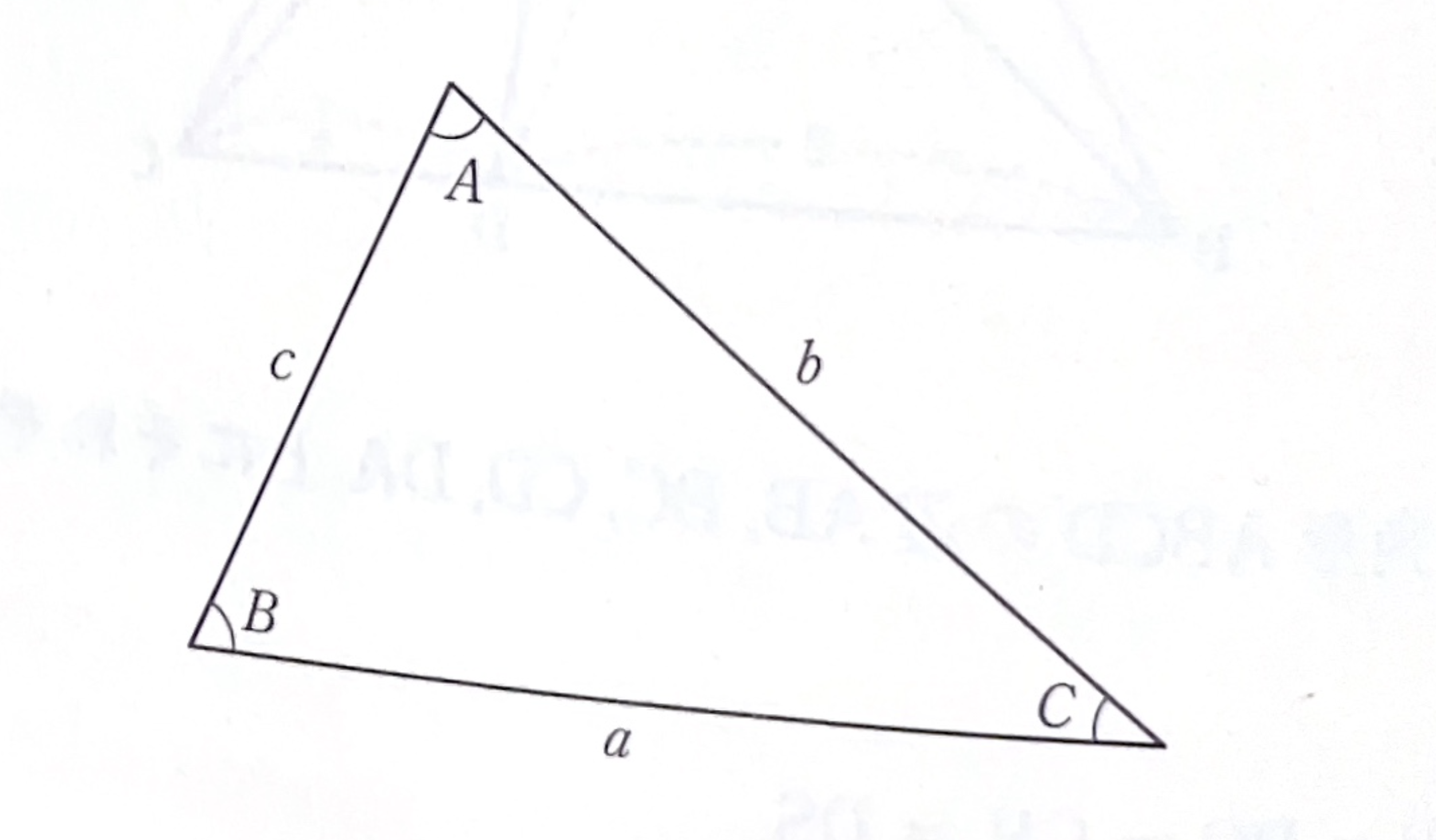
3辺が整数\(a,b,c\)の3角形の3つの角\(A,B,C\)が特別の1次の関係式をもつ場合があります。
もちろん
$$
A+B+C=180^\circ
$$
は当然成立しますが、それと無関係の(線型独立な)関係式で係数が整数のものを見つけて下さい。たとえば図1、図2についてはそのような1次式があります。まずこれみつけてください。
それから、このような1次式をもつ整数の辺の3角形が(相似形をのぞき)他にもあるか、無限にあるか、どのような1次式のものであるか、などについても研究してみてください。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p14-p15.
いざ、チャレンジ
チャレンジの結果…完全論破ではないにせよ、解けました。
割合でいうと8割、といったところでしょうか。
今まで解いてきた「エレガントな解答をもとむ」シリーズでは、特殊例を問題とし、エレガントな解答として、一般化まで踏み込んだ応募者の解答が掲載されている印象があります。
それゆえ一般化したいなと思いましたが、できませんでした。
それがあまりの2割です。
筆者の解答
恥ずかしいお話
なんともお粗末な話なのですが、最初、筆者は題意を正しく読解出来ておらず、無駄なことをしていました…
「読めば分かるじゃん…」という話なのですが。
なんと筆者は最初に三角形の辺の長さに関する等式を導け、だと勘違いして(という保身のための言葉を使いましたが単純におバカでした)いました。
題意は「角に関する等式を導け」ですので、一部無為な時間を過ごしてしまいました。
最初に間違って「なんだ。幾何の問題と見せかけて合同式の問題じゃん。」と解釈した自分が恥ずかしいです。
ここではその間違って解釈した部分については省略します。
では、筆者の回答に行きます。
図1の三角形について

まずは、\(\angle A\)、\(\angle B\)、\(\angle C\)が特別な角度かもしれない、と思い、余弦定理を使って各角の\(\cos\)を計算しました。
- \(\angle A\)について
\begin{eqnarray}
36&=&16+25-2\times20\cos A\\
&=&41-40\cos A
\end{eqnarray}
により、
$$
\cos A=\frac{1}{8}
$$
となり、特別な角ではないことが分かりました。 - \(\angle B\)について
\begin{eqnarray}
25&=&36+16-2\times24\cos B\\
&=&52-48\cos B
\end{eqnarray}
により、
$$
\cos B=\frac{9}{16}
$$
となり、これも特別な角ではないことが分かりました。 - \(\angle C\)について
\begin{eqnarray}
16&=&25+36-2\times30\cos C\\
&=&61-60\cos C
\end{eqnarray}
により、
$$
\cos C=\frac{3}{4}
$$
となり、これも特別な角ではないことが分かりました。
どうやら特殊な角では無いようなので、この方法は適切でないようだ、ということが分かりました。
ということで、補助線を引いて「どことどこの角が合同で…」と三角形やら四角形やらの性質を使うという方法にシフトしました。
で、初手ですが、得られている情報は各辺の長さだけです。
ということはこの長さを使ってなんとか角同士の関係を導出しなければならないわけです。
となると、やはり、うまい具合に補助線を引いて、合同やら相似やらの三角形を見つけて角における関係式を導出する、というのが正攻法だろう、と思いました。
与えられている情報は辺の長さのみなので、「どうにかこの情報を有益に使う補助線はないかな?」と考えたときに真っ先に思い浮かんだのが角の二等分線です。
頂角の二等分線と底辺の交点は、底辺をその他の辺の比で内分する点と一致するためです。
(※勿論、この時点ではこの方法が有益な方法かどうかは分からず、とりあえずやってみるという具合でしたが、結局見立ては正しかったようです、とネタバラシしておきます。)
では、\(\angle A\)、\(\angle B\)、\(\angle C\)のどの角の二等分線を補助線として作図するか、とう話になります。
各辺の長さを確認すると、
$$
AB=4,\quad BC=6,\quad CA=5
$$
です。
先程述べたように、頂角の二等分線は底辺をその他の辺の比で内分する点で底辺と交わります。
それを見越して考えてみます。
\begin{eqnarray}
&&AB+CA=4+5=9,\\
&&AB+BC=4+6=10,\\
&&BC+CA=6+5=11
\end{eqnarray}
と計算できます。
この計算結果を見てみると、\(AB+BC=10=2AC\)となっているため、\(\angle B\)の二等分線とを考えるのが良さそうです(計算しやすいという意味で)。
実際、
$$
AB:BC=4:6=2:3
$$
ですから、\(2+3=5=AC\)となって、比がそのまま長さになってくれました。
というわけで、\(\angle B\)の二等分線と辺\(AC\)との交点\(D\)とします。
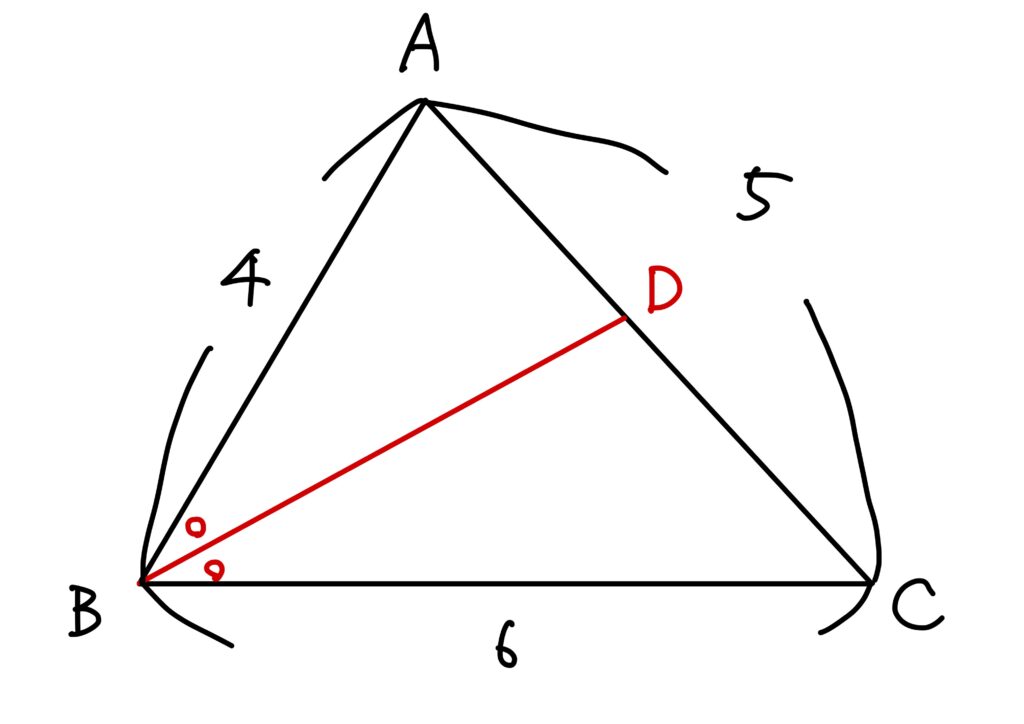
では、新たに作った\(\triangle ABD\)と\(\triangle BDC\)を観察してみます。
しかし、\(\triangle ABD\)と\(\triangle BDC\)は合同はおろか、相似にもなりえません。
故に別の補助線が必要です。
今度は、新たに作った点\(D\)を活用して補助線を引き、三角形を作ることにしました。
\(D\)を経由して補助線を引くとなると、線の引き方は大きく分けて2パターンしかありません。
それは
- 辺\(AB\)上に引く。
- 辺\(BC\)上に引く。
始点を\(D\)とするとき、新たに三角形を作るには辺\(AB\)か辺\(BC\)をめがけて引くほかありません。
勿論、補助線を更に追加すると成るとその限りではありませんが、図形が複雑になり、むしろ考えにくい可能性があります。
今行っている方法で上手く行かなかった場合は、それを考えてみることにしました(結果的に杞憂でしたが)。
さて、辺\(AB\)と辺\(BC\)のどちらに向けて補助線を引くか、という話ですが、迷いどころです。
とはいえ、パターンが2つしか無いので、双方試せばいいかな、と思いました。
まず、\(D\)から\(AB\)にめがけて補助線を引いてみることにしました。
今度は、問題はどのような条件で引くか、ということになります。
そこで\(AD\)の長さに注目すると、\(2\)で、ちょうど\(AB\)の長さの半分です。
この情報を使うことにして、\(AB\)の中点を\(E\)として線分\(DE\)を作図しました。
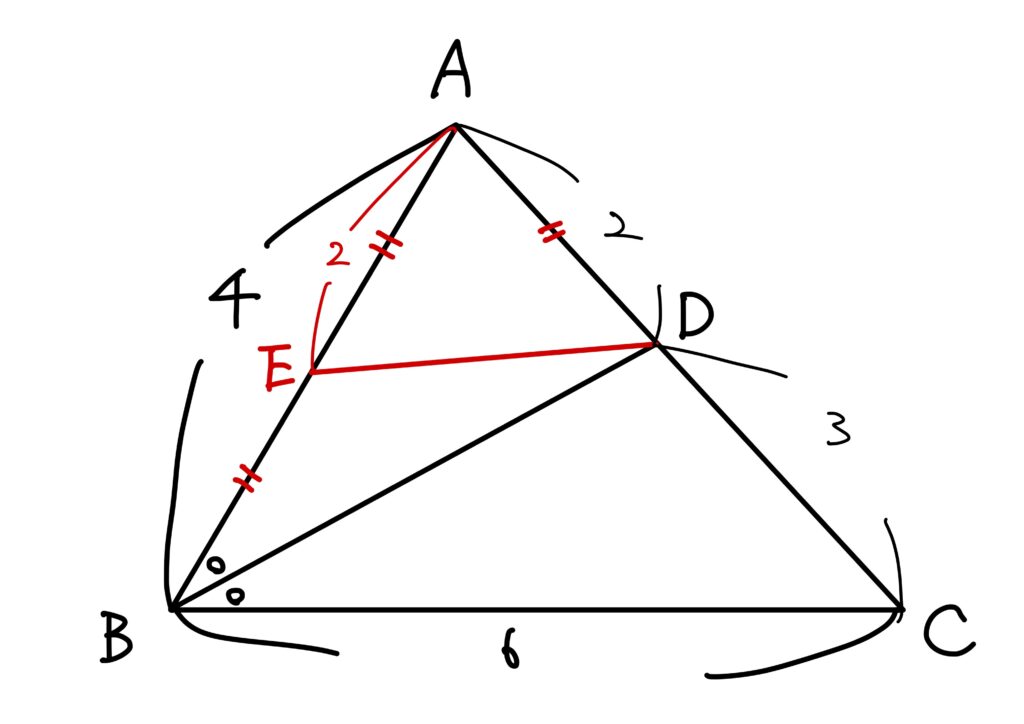
すると、\(AD=AE=2\)となるので、\(\triangle AED\)は二等辺三角形です。
「よしよし。いい感じだぞ。」と思いました。
しかしながら問題があります。
それは「どうやって\(\angle C\)を絡めるか?」ということです。
新たにできた四角形\(EBCD\)に着目しても、特に\(\angle A\)と\(\angle C\)をつなげるような情報は得られなさそうです(もしかしたら得られるかもしれませんが、筆者は得られなさそうだな、と思いました)。
そこで、今度は\(\angle ADB\)の二等分線と\(AB\)の交点を新たに\(E\)として\(DE\)を作図しました。

最初に\(\displaystyle\cos A=\frac{1}{8}\)と求めていたので、
$$
BD^2=4+16-2\cdot8\cdot\frac{1}{8}=18
$$
となり、\(18\)は平方数でなく、他の辺の長さと特に関係なさそうな長さなので、\(D\)から\(AB\)に向けて補助線を引くのは一旦やめました。
次に、\(D\)から\(BC\)にめがけて補助線を引いてみることにしました。
今度も、問題はどのような条件で引くか、ということです。
先程と同様に\(BC\)の中点を\(E\)として線分\(DE\)を作図してしまうと、本質的に先ほどと同じことになってしまいます(各辺の長さが異なるだけで、回転させると同じことをしています)。
故に、別の発想が必要です。
そこで筆者は単純に「\(BC\)上に\(CE=CD\)となるような点\(E\)を取ると良くないのであれば、別の側、つまり\(AB=BE\)となるように\(BC\)上に点\(E\)を取ってみるか?」と思い、取りました。
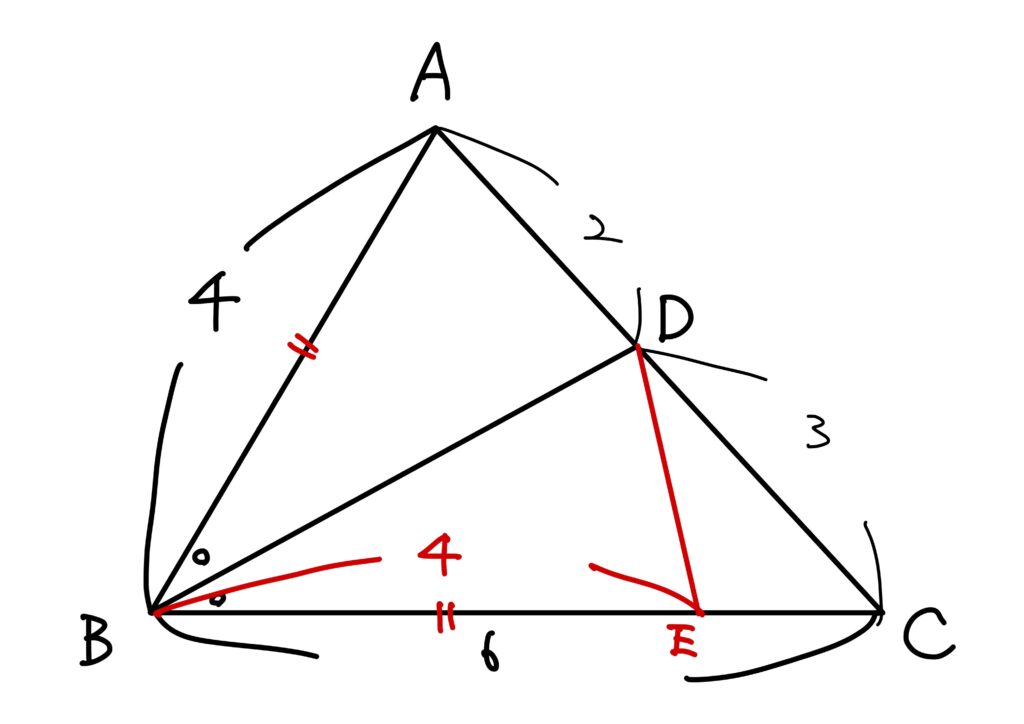
すると、なんとこの方法で解決できました。

二辺夾角合同により、\(\triangle ABD\equiv \triangle EBD\)です。
故に、\(\angle A\equiv\angle BED\)、\(AD\equiv DE\equiv 2\)です。
従って、\(DE\equiv EC\equiv2\)により\(\triangle CDE\)は二等辺三角形だから\(\angle C\equiv \angle CDE\)です。
線分\(BC\)は\(\triangle CDE\)の辺\(EC\)を延長したものと捉えれば、\(\angle BED\)は\(\triangle CDE\)の外角だから
$$
\angle BED\equiv\angle C+\angle CDE\equiv\angle C+\angle C\equiv2\angle C
$$
です。
今、\(\angle A\equiv\angle BED\)だから、\(\angle A\equiv 2\angle C\)です。
…読者の皆様がおっしゃりたいことは分かります。
「”\(D\)から\(BC\)にめがけて\(AB=BE\)となるように\(BC\)上に点\(E\)を取ってみる”というのはすぐ分かるんじゃないか?こんな右往左往しなくてもすぐ分かるんじゃない?」とお思いだと感じます。
そのとおりです。
筆者にもうすこし眼力があれば….
図2について

図1のときと同様に考えました。
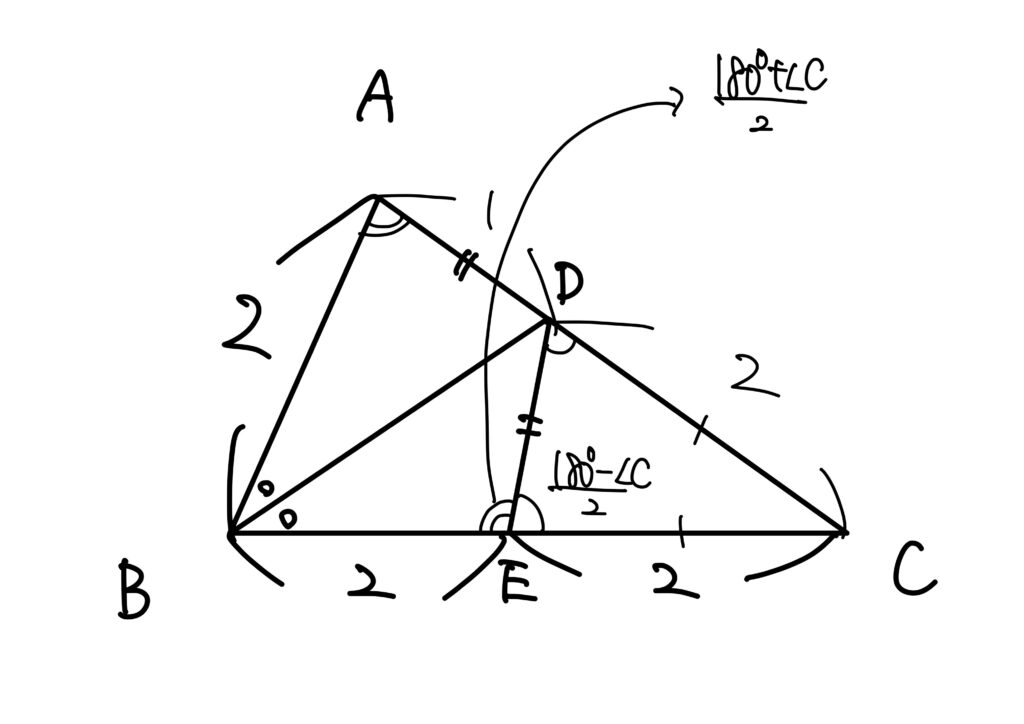
すると、
$$
\angle A\equiv=\angle BED\equiv180^\circ-\angle CED=\frac{180^\circ+C}{2}
$$
という関係式が得られます。
\(\angle A+\angle B+\angle C\equiv 180^\circ\)だから、
$$
\angle A=\frac{\angle A+\angle B+\angle C+\angle C}{2}=\frac{\angle A+\angle B+2\angle C}{2}
$$
により
$$
\angle A-\angle B\equiv 2\angle C
$$
です。
この方法をに気がつけば、図1と図2とは異なる別の角のいち次式を持つ三角形は無限に存在することが分かります。
ここで時間切れでした。
一般化はかないませんでした。
投稿されたエレガントな解答
ほとんどの方が3角比の公式を用いて予想および証明をしていました。 余弦定理と倍角公式より図1の\(A-2C=0\)の成立条件として $$a^2=c(b+c)$$ を求め、\(a,b,c\)を既約な自然数として
\((a,b,c)=(\alpha\gamma,\alpha^2-\gamma^2,\gamma^2)\)の一般解を求めています。 同様に図2の\(A-B-2C=0\)の成立条件としては
\(\large(\alpha,\gamma\)は互いに素な自然数で\(\displaystyle\frac{\alpha}{2}<\gamma<\alpha\large)\)\((a,b,c)=(\alpha^2,\alpha^2-\gamma^2,\alpha\gamma)\)を得ました。
\((\alpha,\gamma\)は互いに素な整数で\(\alpha^2-\alpha\gamma<\alpha^2-\gamma^2<\alpha^2+\alpha\gamma)\)
初等幾何的なものはわずかでした。
(中略)
図1、図2のどちらにも、角\(B\)の2等分線と\(AC\)との交点\(M\)、\(BC\)上で\(BA=BN\)を満たす点\(N\)をとります。 すると\(AM:MC=BA:BC\quad\)および\(\quad \triangle ABM\equiv\triangle NBM\)から\(\triangle NMC\)が2等辺3角形となることがわかります。(図3、図4)
図3の3角形では、 $$ A=\angle BNM=\angle NMC+\angle NCM=2C $$図4の3角形では、 $$ A=\angle BNM=180^\circ-\angle CNM=\frac{180^\circ+C}{2} $$ となります。 また、\(\triangle NMC\)を別の2等辺3角形に取り替えれば、このタイプの3角形が無限に存在することも分かります。
この証明に気づくと、図1、図2とは別種の角の1次式をもつ3角形も無限に発見することが出来ます。
(中略)
さらにこれを一般化して、
定理 3辺が\(a_n,b_n,c_n\)の3角形の角\(A_n,B_n,C_n\)が $$ \alpha_nA_n+\beta_nB_n+\gamma_nC_n=0 $$ の関係を持つならば、3辺が $$ (a_{n+1},b_{n+1},c_{n+1})=(a_nb_n,b_n^2-c_n^2,a_nc_n) $$ の3角形の角\(A_{n+1},B_{n+1},C_{n+1}\)について $$ \alpha_{n+1}A_{n+1}+\beta_{n+1}B_{n+1}+\gamma_{n+1}C_{n+1} $$$$ =\alpha_nA_{n+1}+\beta_nB_{n+1}+(-\alpha_n+\beta_n+\gamma_n)C_{n+1}=0 $$ なる関係を持つ。
を得ています。 (\(\triangle MNC\)の向きを変えれば、あと2つの漸化式が得られる)
(中略)
氏は、次の定理をつきとめました。
定理 任意の自然数\(m,n\)について、\(mA-nB=0\)を満たす整数辺の3角形が無数にある。
(中略)氏の証明をスケッチすると以下のようになります。これだけでも十分期待以上だったのですが、なんと(中略)氏は「完全解」をつきとめてしまいました。 次のとおりです。
- \((a,b,c)=(x^2+y^2,x^2-y^2,2xy)\quad (x,y\)は自然数\()\)
なる\(a,b,c\)は直角3角形の3辺を与える。- 1.の\(a,b,c\)にたいし\(\displaystyle\cos\alpha=\frac{b}{a}\)、\(\displaystyle\sin\alpha=\frac{c}{a}\)なる角\(\alpha\)をとると、\(\cos\alpha\)、\(\sin\alpha\)がともにゆうりすうとなる角\(\alpha\)が稠密に存在することがわかる。
- \(\alpha\)と自然数\(k\)に対し、\(\sin k\alpha\)は有理数。
- \(A=n\alpha\)、\(B=m\alpha\)、\(C=\pi-(n+m)\alpha\)とおくと $$ a:b:c=\sin A:\sin B:\sin C $$ は有理数比すなわち整数比。
定理 \(\triangle ABC\)が\(xA+yB-xC=0\ (x,y,z\)は\(x>0\)、\(y\geq0\)、\(z>0\)なる整数で互いに素\()\)の関係を持つとき、\(a:b:c\)が整数比となる必要十分条件は、\(x+z\)と\(y+z\)の最大公約数が\(3\)以下であることである。
証明はレポート用紙10枚にもわたる大作(正直びっくりしちまった!)なので、もれなく掲載するわけにはいきません。 粗いスケッチでお許しください。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p97-p101.
- 3辺\(a,b,c\)が整数比であるための必要十分条件は、\(\cos A\)、\(\cos B\)、\(\cos C\)すべてが有理数なことである。
- \(n\)を任意の整数としたとき、\(\cos X\)が有理数ならば\(\cos nX\)は有理数、\(\sin nX\)は\(\sin X\times\)(有理数)の形になる。
- \(\cos D\)が有理数であるような角\(D\)があり、3角形の3角\(A,B,C\)が自然数\(k,l,m,n\)を使って次のように表せたとすれば、この3角形の3辺の比は整数比である。(ただし、\(n\)と\(m\)は互いに素) \begin{eqnarray} &&A=mD-(l-1)\pi,\quad B=k\pi-nD,\\ &&C=(n-m)D+(l-k)\pi\tag{\(\ast\)} \end{eqnarray}
- \((\ast)\)の\(A,B,C\)が3角形の3角を成す条件は $$ D>\frac{l-1}{m}\pi,\quad D<\frac{k}{n}\pi,\quad D>\frac{k-l}{n-m}\pi. $$ このような角\(D\)が存在する条件は $$ n>nl-mk>0. $$
- 4.の条件下で\((\ast)\)のように\(A,B,C\)を作ると $$ nA+mB=P\pi\quad\left(P=n-(nl-mk) \right) $$ あるいは\(A+B+C=\pi\)を用いて $$ (n-P)A+(m-P)B-PC=0 $$ が得られる。
- 逆に角の間に
\(xA+yB-zC=0\quad\tag{\(\star\)}\)が成立するとする。 \(x+z\)と\(y+z\)が互いに素であれば $$ n=x+z,\quad m=y+z $$ とおくと、4.の条件を満たす\(l,k\)が存在し、したがって\((\star)\)をみたす3角形で辺が整数比のものが無限に存在する。
\((x,y,z\)は整数で互いに素、\(x>0\)、\(y\geq0\)、\(z>0\)、\(x\geq y)\)- \(x+z\)と\(y+z\)が4以上の共通因子\(s\)を持つとする。 $$ nA+mB=s(n^\prime A+m^\prime B)=z\pi $$ から
\(\displaystyle\cos(n^\prime A+m^\prime B)=\cos\frac{z}{s}\pi.\quad\)(\(z\)と\(s\)は互いに素)ここで\(\displaystyle\cos\frac{z}{s}\)は\(s\geq4\)において無理数より、左辺は無理数となる。 よって、1.,2.より辺の比は整数比ではありえない。- \(x+z\)、\(y+z\)の最大公約数が2または3の場合は、整数比の3角形は無数に存在する。
いやあ、世の中にはすごいお方がいらっしゃるもんですね。
この問題を完全に論破するというのはまさしくエレガントと言えるでしょう。
個人的に数学の面白いところの1つとして、この問題のように「問題文(主張)はシンプルだけど、考えることや導かれる事実の量が多い」があると思います。
読者の皆様への挑戦状!
今から紹介する問題の解答は今週の土曜日に解説します!
一郎君は、軸と軸受が同心円でないのに、ベアリングを入れようと考えました。ヤマカンで選んだ場所から出発して順次、軸と軸受と直前のベアリングに接するようにベアリングの球の大きさを変えながら入れていくと、なんと最後のベアリングが最初のベアリングにちゃんと接しました。ラッキー!
しかし、このような幸運に恵まれたときは、実はどこからベアリングを入れ始めてもちゃんとベアリングの輪は完結するのです。これを証明して下さい。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p15.
皆様の挑戦をコメントでお待ちしております!
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!





コメントをする