本記事の内容
本記事はベキ級数とその収束半径についてを解説する記事です。
本記事を読むにあたり、級数の収束について知っているとより理解が深まると思われますので、以下の記事も合わせて御覧ください。
本記事を読む前に…
ベキ級数についてはそんなに量は多くないのですが、テイラー展開を単に公式のよう終わらせることなる、一歩踏み込んだ議論をしたいので、テイラー展開に必要な部分だけをエクストリームで解説します。
ベキ級数とは何かネ?
まずは「ベキ級数とはなんぞや?」という話ですが、
$$
a_0+a_1(x-a)+a_2(x-a)^2+\cdots =\sum_{n=0}^\infty a_n(x-a)^n
$$
という形の級数をベキ級数といいます。
より厳密には、\(a\)を中心とするベキ級数といいます。
本来は\(a_0,a_1,\dots ,a_n,\dots,x\)は複素数で考えるのですが、今回はこれらすべてが実数の場合を考えます。
次回解説するテイラー展開にはこのベキ級数が出現します。
ベキ級数は見ての通り、関数です。
前回、級数の収束について解説しました。
級数の収束は\(a_n\)についてだけ目を向ければよかったのですが、ベキ級数の場合は\(x\)の値によって収束したり収束しなかったりということが起こります。
では、どういうときにベキ級数は収束するのか、すなわち、\(x\)がどの範囲内にあるときに収束するのかということと、その求め方の1部を説明します。
まずは例
おそらく一番簡単な例は以下です。
例1. ある\(a\in\mathbb{R}\)に対して、\(\displaystyle\sum_{n=0}^\infty (x-a)\)というベキ級数を考えます。
これは前回説明したとおり、以下が成り立つことを思い出せば、どの範囲の\(x\)で収束するか、ということがわかると思います。
証明は【解析学の基礎シリーズ】級数とベキ級数編 その1を御覧ください。
つまり、\(|x-a|<1\)のときに\(\displaystyle\sum_{n=0}^\infty (x-a)\)は収束します。
この場合、収束半径は\(1\)です。
収束半径のイメージは何かネ?
では、収束半径について解説します。
一言で言えば、
です。
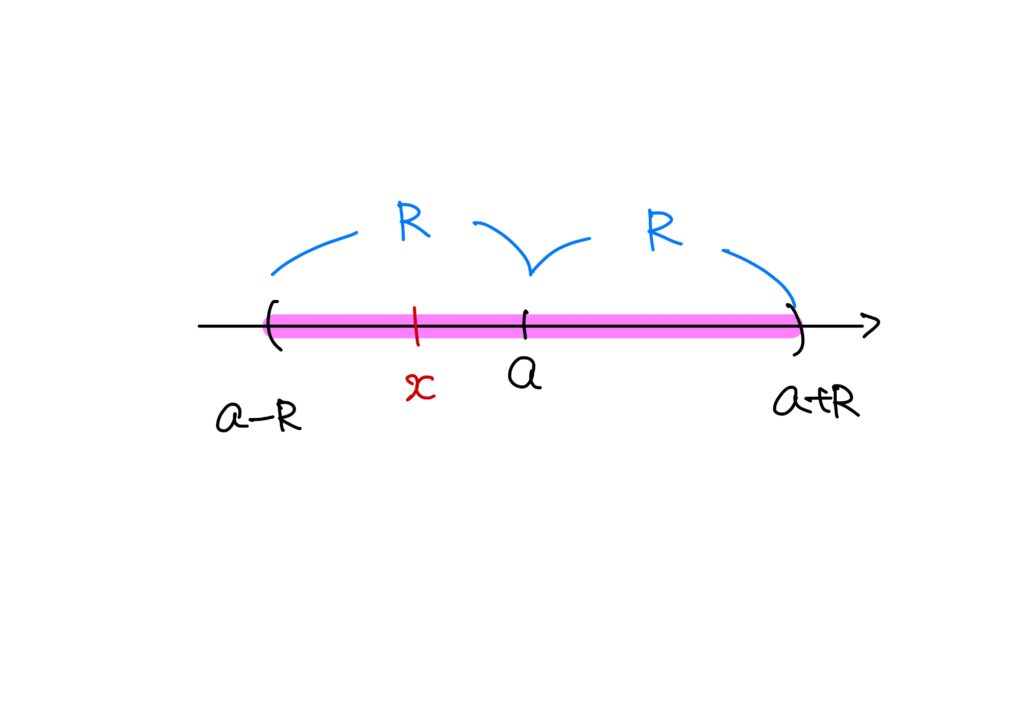
「ん?」と思うかもしれませんが、「\(|x-a|<R\)という範囲でベキ級数が収束するときの\(R\)のこと」です。
ここで、一つ疑問が生まれます。
です。
大丈夫です。担保されています。
次節でそれを解説します。
どんなベキ級数に対しても、必ず\(|x-a|<R\)という\(R\in\mathbb{R}\)の存在が担保されてるのかネ?
では、解説します。
「担保されていますよ、局長。」と言い切れるのは次の定理が成り立つからです。
- \(|x-a|<R\)ならば、\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)は絶対収束する。
- \(|x-a|>R\)ならば、\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)は収束しない。
定理2.の証明
ベキ級数\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)が収束するような\(x\)の集合を\(S\)、\(A=\{|x-a|\mid x\in S\}\)と記すことにします。
仮に、\(A\)が上に有界なのであれば、\(R=\sup A\)として、\(A\)が上に有界でなければ、\(R=\infty\)と置きます。
\(R>0\)であれば、\(|x-a|<R\)となる任意の\(x\in\mathbb{R}\)に対して、\(|x-a|<|x_0-a|<R\)という\(x_0\)が存在します。
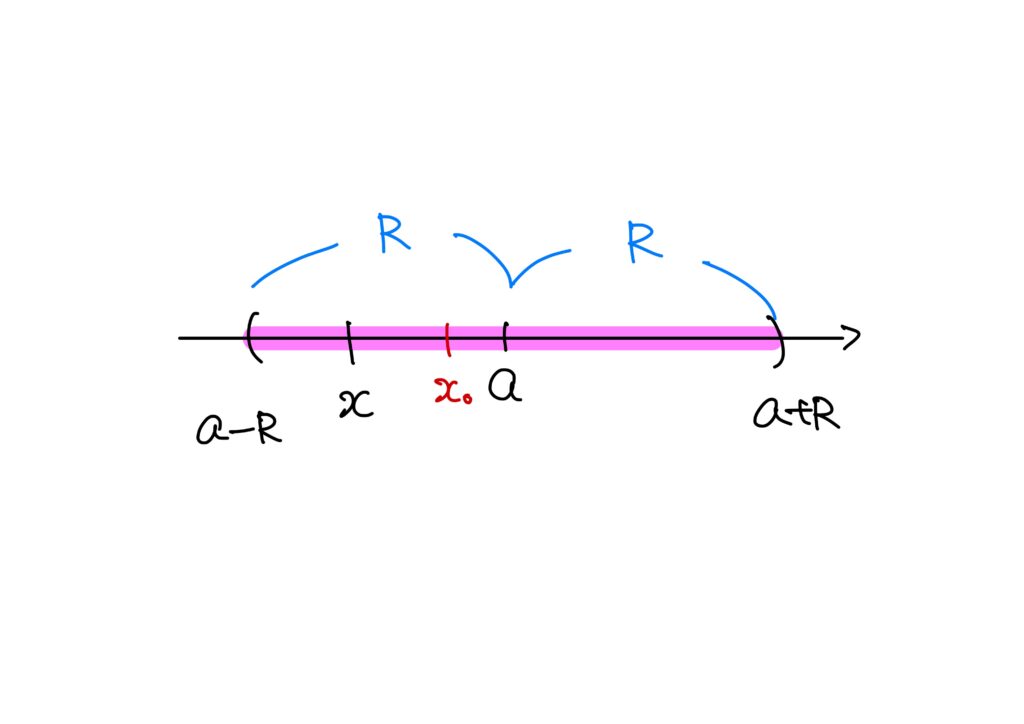
今、\(|x_0-a|<R=\sup A\)ですので、級数\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)は\(x=x_0\)で収束します。
このとき、\(a_n(x_0-a)^n\to0\)(\(n\to \infty\))です。
なぜならば、次が成り立つからです。
補題3.の証明
\(\displaystyle s_n=\sum_{n=0}^n a_n\)とします。
今、\(\displaystyle \sum_{n=0}^\infty a_n\)が収束するので、\(\displaystyle \lim_{n\to\infty}s_n\)が収束します。
その収束先を\(\alpha\)とします。
今、\(s_{n-1}\)も\(\alpha\)に収束するので、\(a_n=s_n-s_{n-1}\to\alpha-\alpha=0\)です。
補題4.の証明終わり
定理2.の証明に戻ります。
定理2.において補題4.から\(a_n(x_0-a)^n\to0\)(\(n\to \infty\))です。
さらに、\(a_n(x_0-a)^n\to0\)により、\(a_n(x_0-a)^n\)は収束するので、有界です。
実際、次が成り立つからです。
補題5.の証明
なんてことありません。
\(\displaystyle\lim_{n\to\infty}a_n=\alpha\)とします。
すると、
$$
(\forall \epsilon>0)\ (\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_n-\alpha|<\epsilon)
$$
です。
ここで、\(K=\max\{|a_1|,|a_2|,\dots,|a_{N-1}|,|\alpha|+\epsilon\}\)と定めると、任意の\(n\in\mathbb{N}\)に対して\(|a_n|\leq K\)です。
すなわち、有界です。
補題5.の証明終わり
定理2.の証明に戻ります。
補題5.から、\(a_n(x_0-a)^n\)は有界です。
故に、ある\(M>0\)が存在して、任意の\(n\in\mathbb{N}\)に対して、
$$
|a_n(x_0-a)^n|\leq M
$$
すなわち、
$$
|a_n|\leq M\cdot \frac{1}{|(x_0-a)^n|}
$$
です。
故に、
$$
|a_n(x-a)^n|\leq M\cdot \left| \frac{x-a}{x_0-a} \right|^n
$$
が任意の\(n\in\mathbb{N}\)で成り立ちます。
今、\(\displaystyle\left|\frac{x-a}{x_0-a}\right|<1\)ですので、右辺を第\(n\)項とする\(\displaystyle\sum_{n=0}^\infty a_n\)は収束します。
従って、以下の比較定理の1.から\(x\)において絶対収束します。
- 任意の\(n\in\mathbb{N}\cup\{0\}\)に対して\(a_n\leq c_n\)ならば\(\displaystyle\sum_{n=0}^\infty a_n\)は収束する。
- 任意の\(n\in\mathbb{N}\cup\{0\}\)に対して\(a_n\geq d_n\)ならば\(\displaystyle\sum_{n=0}^\infty a_n\)は発散する。
- 任意の\(n\in\mathbb{N}\cup\{0\}\)に対して\(\displaystyle\frac{a_{n+1}}{a_n}\leq \frac{c_{n+1}}{c_n}\)ならば\(\displaystyle\sum_{n=0}^\infty a_n\)は収束する。
- 任意の\(n\in\mathbb{N}\cup\{0\}\)に対して\(\displaystyle\frac{a_{n+1}}{a_n}\geq \frac{d_{n+1}}{d_n}\)ならば\(\displaystyle\sum_{n=0}^\infty a_n\)は収束する。
ちなみに\(R=0\)であれば、\(S=\{a\}\)です。
次に\(|x-a|>R\)であれば、\(x\not\in S\)です。
すなわち、\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)は収束しません。
最後に一意性について証明します。
今、1.および2.を満たすような\(R^\prime\)が存在して、かつ\(R\neq R^\prime\)だとします。
このとき、\(R<R^\prime\)かまたは\(R^\prime<R\)のいずれかが成り立ちます。
仮に、\(R<R^\prime\)としましょう。
このとき、\(R\)と\(R^\prime\)の間にある実数\(r\)が存在します(例えば、\(\displaystyle r=\frac{R+R^\prime}{2}\)です)。
ここで、\(x=a+r\)と置きます。
このとき\(x\in\mathbb{R}\)で、\(R<r=|x-a|<R^\prime\)です。
そこで、\(R\)が2.を満たしているので、\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)は\(x\)で発散します。
一方で、\(R^\prime\)が1.を満たしていることから\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)は\(x\)で収束しまい、矛盾です。
同様に\(R^\prime<R\)のときも矛盾が導かれます。
以上のことから\(R=R^\prime\)でなければなりません。
従って一意的です。
定理2.の証明終わり
定理2.が成り立ったので、どんなベキ級数に対しても、必ず\(|x-a|<R\)という\(R\in\mathbb{R}\)の存在が担保されています。
収束半径は数学的に何かネ?
「数学的に何かネ?」と言われても実は収束半径とは、定理2.における\(R\)です。
“半径”という言葉を使っているので、「円かな?」と思うかもしれませんが、1次元の場合は区間で、2次元だと円で、3次元だと球です。
ちなみに、\(|x-a|=R\)を満たすような\(R\)を収束円周といいます。
\(R=0\)の場合は\(x=a\)以外の点では収束しません。
収束半径を求める方法
\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)の係数\(a_n\)から収束半径\(R\)を求める一般の方法としてコーシー-Hadamard(コーシー-アダマール)の収束判定法がありますが、ここでは述べません。
というのも、少々込み入った話に入ってしまうからです。
そこで、特別な場合のみ収束半径\(R\)を与える簡単な方法を1つ紹介します。
この定理の証明には前回証明したratio testを使います。
ratio testとは何だったかというと以下でした。
定理8.の証明は【解析学の基礎シリーズ】級数とベキ級数編 その1を御覧ください。
では、定理7.の証明に入ります。
定理7.の証明
\(x\neq a\)として、正項級数\(\sum_{n=0}^\infty |a_n(x-a)^n|\)に定理8.(ratio test)を適用します。
今、
$$
\lim_{n\to\infty}\left|\frac{a_n}{a_{n+1}}\right|=R\in[0,\infty]
$$
により、
$$
\lim_{n\to\infty}\left|\frac{a_{n+1}(x-a)^{n+1}}{a_n(x-a)^n}\right|=\lim_{n\to\infty}\left|\frac{a_{n+1}(x-a)}{a_n}\right|=\frac{|x-a|}{R}
$$
です。
ただし、\(R=0\)のとき、右辺は\(\infty\)となります。
さて、さらに定理8.(ratio test)から
- \(\displaystyle\frac{|x-a|}{R}<1\)のとき、すなわち、\(|x-a|<R\)のときに収束、
- \(\displaystyle\frac{|x-a|}{R}>1\)のとき、すなわち、\(|x-a|>R\)のときに発散
します。
最後にこの\(R\)が収束半径であることを証明します。
仮に、\(R^\prime\)が\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)の収束半径だとしましょう。
つまり、\(R=R^\prime\)が証明できれば完了です。
今、\(|x-a|<R\)ですので、\(R\leq R^\prime\)です。
実際、仮に\(R^\prime<R\)だったとすると、\(R^\prime<|x-a|<R\)となるような\(x\)をとれば、\(|x-a|<R\)に矛盾してしまいます。
また、\(R<R^\prime\)だとすると\(R<|x-a|<R^\prime\)となる\(x\)が存在します。
\(R<|x-a|\)だから、\(x\)では\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)は絶対収束しません。
一方で、\(|x-a|<R^\prime\)ですので、\(x\)で\(\displaystyle\sum_{n=0}^\infty a_n(x-a)^n\)が絶対収束してしまい矛盾です。
従って、\(R=R^\prime\)となって\(R\)は収束半径です。
定理7.の証明終わり
結
今回はベキ級数とその収束半径について解説しました。
これはテイラー展開において、テイラー展開が収束する範囲を知るために必要です。
言ってしまえば、「あまりにも遠い場所ではうまく近似できませんよ」といっていて、”遠い”とは収束半径外ということなのです。
次回はテイラー展開の代表例を単に公式としてではなく収束半径も加味して解説します。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする