本記事の内容
本記事は点列の内積の極限について解説する記事です。
この記事を読むにあたり、「点列って?」「点列の極限って?」ということを知っている必要があるため、その際は以下の記事を参照してください。
では、早速行きましょう!
点列の極限のチャラい復習
点列の極限をチャラく復習しましょう。
点列は数列の多次元バージョンでした。
つまり、数列の値は実数でしたが、点列の値はベクトルというわけでした。
数列の極限は極限(実数)への近づき方が直線的だったのに対して、点列の極限は極限(ベクトル)への近づき方が空間的(ありとあらゆる方向から近づく)なのでした。
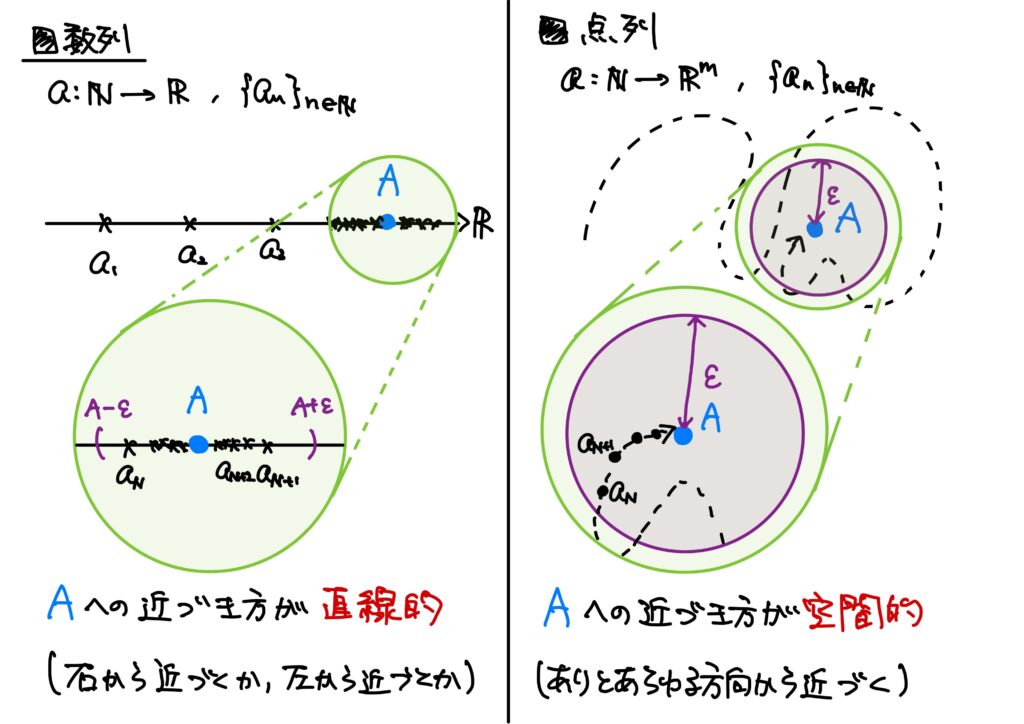
さらに、以下の定理が成り立つのでした。
つまり、点列の極限は数列の極限に帰着できる、ということでした。
前回は点列の和・差の極限と点列の数列倍の極限について解説しました。
今回は和差積商のうちの積に対応する点列の極限について解説します。
ただし、ベクトル同士は単純に積を考えることができません。
ベクトルにおける積とはおおよそ内積と外積の2種類です。
内積についてはすでに高校数学で学んでいるので、特に問題は無いかと思いますが外積は大学数学で初めて出現する概念です。
(筆者は高校で初めて内積を学んだとき「外積ってのもあるのかね?」と思っていました。実際ありました。)
今回は内積と外積のうち、内積について説明します。
内積の復習
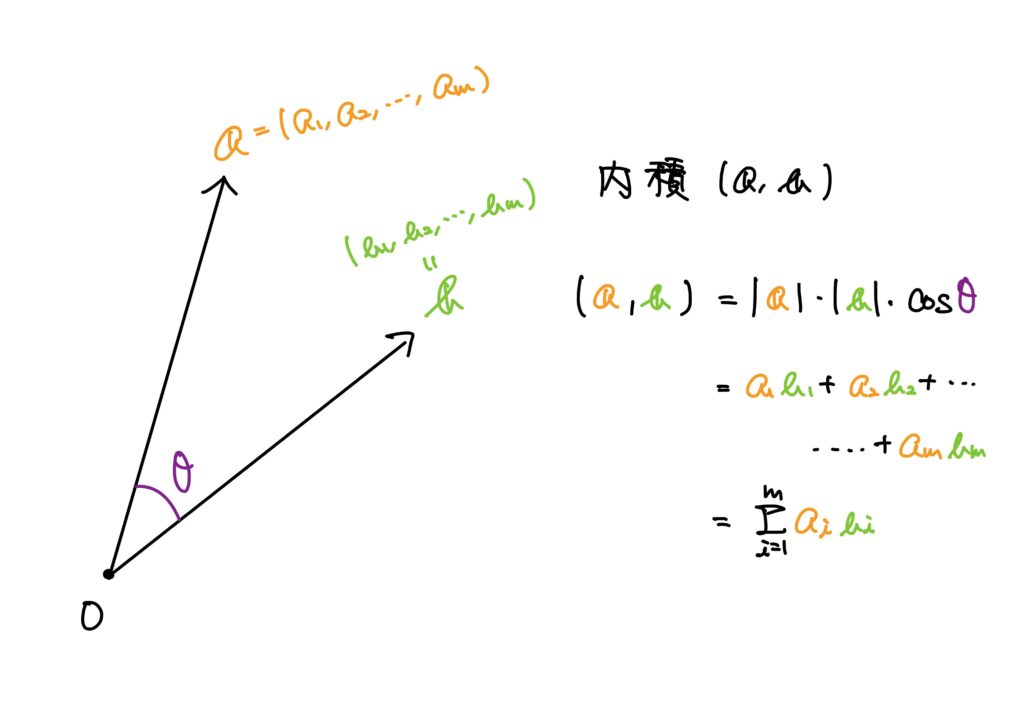
内積は高校数学ですでに触れているのでチャラく復習します。
つまり、「なんだったっけ?」「これです。」と述べるだけに留めます。
\(\boldsymbol{a}=(a_1,a_2,\dots,a_m)\top\)、\(\boldsymbol{b}=(b_1,b_2,\dots,b_m)\top\)とします。
このとき\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の内積\((\boldsymbol{a},\boldsymbol{b})\)は
\begin{eqnarray}
(\boldsymbol{a},\boldsymbol{b})&=&|\boldsymbol{a}|\cdot|\boldsymbol{b}|\cos\theta\\
&=&\sum_{i=1}^ma_ib_i
\end{eqnarray}
でした。
ただし、\(\theta\in[0,\pi]\)は\(\boldsymbol{a}\)と\(\boldsymbol{b}\)のなす角でした。
ここで、内積は\((\boldsymbol{a},\boldsymbol{b})\)という記号の他に\(\boldsymbol{a}\cdot\boldsymbol{b}\)と書かれることもあります。
点列の内積の極限はどうなりそう?(例)
まずは例を考えてみましょう。
例1.
$$\boldsymbol{A}=
\left(
\begin{array}{c}
0 \\
2 \\
\end{array}
\right),\quad
\boldsymbol{a}_n=
\left(
\begin{array}{c}
\displaystyle \frac{1}{n} \\
2 \\
\end{array}
\right),\quad
\boldsymbol{B}=
\left(
\begin{array}{c}
1 \\
1\\
\end{array}
\right),\quad
\boldsymbol{b}_n=
\left(
\begin{array}{c}
\displaystyle 1+\frac{1}{n} \\
\displaystyle \frac{n+2}{n} \\
\end{array}
\right),
$$
とします。
このとき、
$$\lim_{n\to\infty}\boldsymbol{a}_n=A,\quad \lim_{n\to\infty}\boldsymbol{b}_n=B$$
です。
これは前々回(【解析学の基礎シリーズ】点列編 その1)で証明しています。
今、
\begin{eqnarray}
\lim_{n\to\infty}(\boldsymbol{a}_n,\boldsymbol{b}_n)&=&\lim_{n\to\infty}\left\{\frac{1}{n}\left(1+\frac{1}{n} \right)+2\cdot \frac{n+2}{n}\right\}\\
&=&\lim_{n\to\infty}\left(\frac{1}{n}+\frac{1}{n^2} +2+ \frac{4}{n}\right)\\
&=&\lim_{n\to\infty}\left(\frac{1}{n^2}+\frac{5}{n} +2\right)\\
&=&\lim_{n\to\infty}\frac{1}{n^2}+\lim_{n\to\infty}\frac{5}{n}+\lim_{n\to\infty}2\\
&=&2\\
&=&(\boldsymbol{A},\boldsymbol{B})
\end{eqnarray}
です。
これには前回(【解析学の基礎シリーズ】点列編 その2)証明した、収束する数列の和の極限は極限の和と等しいという性質を使っています。
一方で、
\begin{eqnarray}
(\lim_{n\to\infty}\boldsymbol{a}_n,\lim_{n\to\infty}\boldsymbol{b}_n)&=&
\left(\lim_{n\to\infty}\left(
\begin{array}{c}
\displaystyle\frac{1}{n} \\
2 \\
\end{array}
\right),
\lim_{n\to\infty}\left(
\begin{array}{c}
\displaystyle1+\frac{1}{n} \\
\displaystyle\frac{n+2}{n} \\
\end{array}
\right)
\right)\\
&=&\left(\left(
\begin{array}{c}
\displaystyle\lim_{n\to\infty}\frac{1}{n} \\
\displaystyle\lim_{n\to\infty}2 \\
\end{array}
\right),
\left(
\begin{array}{c}
\displaystyle\lim_{n\to\infty}\left(1+\frac{1}{n}\right) \\
\displaystyle \lim_{n\to\infty}\frac{n+2}{n} \\
\end{array}
\right)
\right)\\
&=&\left(
\left(
\begin{array}{c}
0 \\
2 \\
\end{array}
\right),
\left(
\begin{array}{c}
1 \\
1 \\
\end{array}
\right)
\right)\\
&=&2\\
&=&(\boldsymbol{A},\boldsymbol{B})\\
\end{eqnarray}
です。
従って、
$$
\lim_{n\to\infty}(\boldsymbol{a}_n,\boldsymbol{b}_n)=\left(\lim_{n\to\infty}\boldsymbol{a}_n,\lim_{n\to\infty}\boldsymbol{b}_n \right)
$$
が成り立ちそうです。
実際、成り立ちます。
では、証明してみましょう。
点列の内積の極限は点列の極限の内積と等しい
まずは、主張を数学的に明示しましょう。
では、証明しましよう。
とはいえ、前回までの知識を使えば簡単に証明ができます。
証明
$$
\boldsymbol{a}_n=
\left(
\begin{array}{c}
a_{n,1} \\
a_{n,2} \\
\vdots \\
a_{n,m}
\end{array}
\right),\quad
\boldsymbol{b}_n=
\left(
\begin{array}{c}
b_{n,1} \\
b_{n,2} \\
\vdots \\
b_{n,m}
\end{array}
\right),
$$
とします。
このとき、
\begin{eqnarray}
\lim_{n\to\infty}(\boldsymbol{a}_n,\boldsymbol{b}_n)&=&\lim_{n\to\infty}\left(
\left(
\begin{array}{c}
a_{n,1} \\
a_{n,2} \\
\vdots \\
a_{n,m}
\end{array}
\right),
\left(
\begin{array}{c}
b_{n,1} \\
b_{n,2} \\
\vdots \\
b_{n,m}
\end{array}
\right)
\right)\\
&=&\lim_{n\to\infty}(a_{n,1}b_{n,1}+a_{n,2}b_{n,2}+\cdots a_{n,m}b_{n,m})
\end{eqnarray}
ここで、
- \(\displaystyle \lim_{n\to\infty}(a_n+b_n)=\lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n\)
- \(\displaystyle \lim_{n\to\infty}(a_n-b_n)=\lim_{n\to\infty}a_n-\lim_{n\to\infty}b_n\)
が成り立つので(証明は【解析学の基礎シリーズ】点列編 その2を参照)、
\begin{eqnarray}
&&\lim_{n\to\infty}(a_{n,1}b_{n,1}+a_{n,2}b_{n,2}+\cdots a_{n,m}b_{n,m})\\
&=&\lim_{n\to\infty}a_{n,1}b_{n,1}+\lim_{n\to\infty}a_{n,2}b_{n,2}+\cdots +\lim_{n\to\infty}a_{n,m}b_{n,m}
\end{eqnarray}
が成り立ちます。
さらに、
が成り立つので(証明は【解析学の基礎シリーズ】点列編 その2を参照)、
\begin{eqnarray}
&&\lim_{n\to\infty}a_{n,1}b_{n,1}+\lim_{n\to\infty}a_{n,2}b_{n,2}+\cdots \lim_{n\to\infty}a_{n,m}b_{n,m}\\
&=&\left(\lim_{n\to\infty}a_{n,1}\right)\cdot \left(\lim_{n\to\infty}b_{n,1}\right)+\left(\lim_{n\to\infty}a_{n,2}\right)\cdot \left(\lim_{n\to\infty}b_{n,2}\right)+\cdots \left(\lim_{n\to\infty}a_{n,m}\right)\cdot +\left(\lim_{n\to\infty}b_{n,m}\right)\\
&=&\left(
\left(
\begin{array}{c}
\displaystyle \lim_{n\to\infty}a_{n,1} \\
\displaystyle \lim_{n\to\infty}a_{n,2} \\
\vdots \\
\displaystyle \lim_{n\to\infty}a_{n,m}
\end{array}
\right),
\left(
\begin{array}{c}
\displaystyle \lim_{n\to\infty}b_{n,1} \\
\displaystyle \lim_{n\to\infty}b_{n,2} \\
\vdots \\
\displaystyle \lim_{n\to\infty}b_{n,m}
\end{array}
\right)
\right)\\
&=&\left(\lim_{n\to\infty}\boldsymbol{a}_n,\lim_{n\to\infty}\boldsymbol{b}_n\right)
\end{eqnarray}
が成り立ちます。
従って、
$$
\lim_{n\to\infty}(\boldsymbol{a}_n,\boldsymbol{b}_n)=\left(\lim_{n\to\infty}\boldsymbol{a}_n,\lim_{n\to\infty}\boldsymbol{b}_n \right)
$$
です。
証明終わり
結
今回は点列の内積の極限と点列の極限の内積が等しいことを説明し証明しました。
つまるところ、点列は内積を計算してから極限を取ろうが、極限を取ってから内積を計算しようが結果は同じということです。
次回はベクトルの外積と点列の外積の極限について解説します。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする