本記事の内容
本記事は多変数実数値関数の発散の一部を解説する記事です。
本記事を読むにあたり、1変数実数値関数の発散について知っている必要があるため、その際は以下の記事を参照してください。
1変数実数値関数の場合のチャラい復習
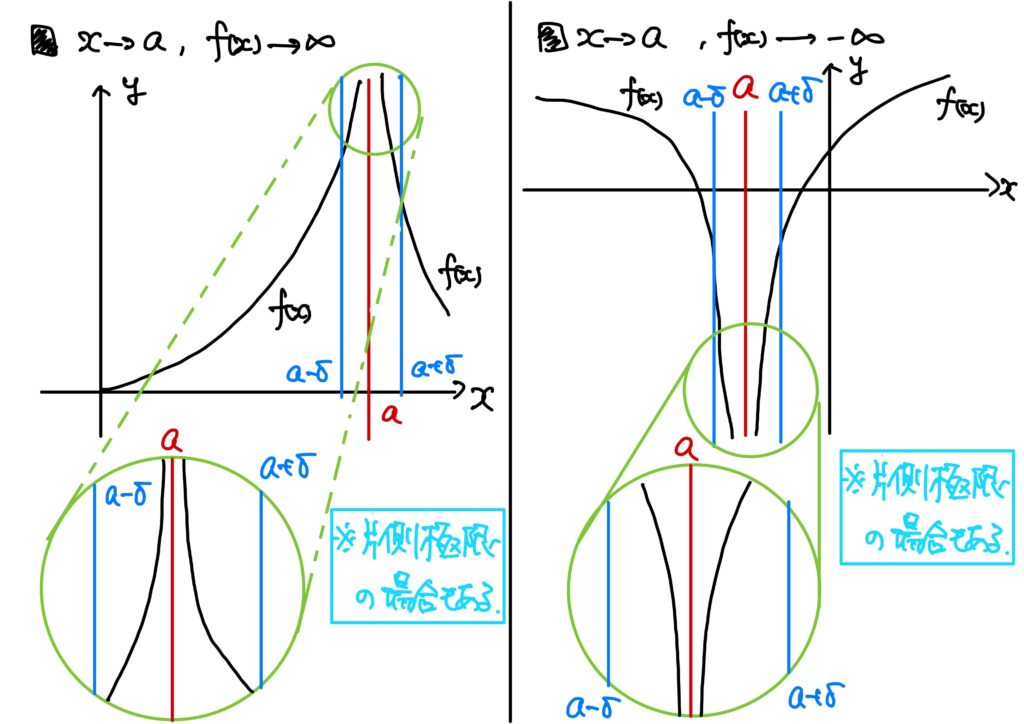
\(x\to a\)のときの\(f(x)\to\infty\)を一言でのべれば、次でした。
「ある点の付近」というのは、「ある点\(a\)との距離が\(\delta\)未満であるような\(x\)に対しては」という意味です。(関数の収束と同じだネ)
“無限大”とはどんな実数よりも大きい数でした。
詳しくは【解析学の基礎シリーズ】数列の発散編 その2を参照してください。
ちなみに、負の無限大も同じです。
以上のことを論理式で書くと以下になります。
- \(\infty\)への発散 関数\(f\)が\(x\to a\)のとき\(\infty\)(正の無限大)に発散するとは、次が成り立つことをいう。 $$(\forall U\in\mathbb{R})(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-a|<\delta\Rightarrow f(x)>U)$$ このとき、 $$\lim_{x\to a}f(x)=\infty$$ と書く。
- ある点付近での\(\infty\)への発散 関数\(f\)が\(x\to a\)のとき\(-\infty\)(負の無限大)に発散するとは、次が成り立つことをいう。 $$(\forall L\in\mathbb{R})(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-a|<\delta\Rightarrow f(x)<L)$$ このとき、 $$\lim_{x\to a}f(x)=-\infty$$ と書く。
多変数実数値関数の場合
形式的には1変数の場合とほとんど変わりません。
というより、区間が領域になって\(x\)と\(a\)がそれぞれベクトルになるだけです。
多変数実数値関数の場合の、ある点付近での発散もまた、
ということです。
では早速数学的に主張を明示してしまいましょう。
- \(\infty\)への発散 関数\(f\)が\(\boldsymbol{x}\to\boldsymbol{a}\)のとき\(\infty\)(正の無限大)に発散するとは、次が成り立つことをいう。 $$(\forall U\in\mathbb{R})(\exists \delta>0)\ {\rm s.t.}\ (\forall \boldsymbol{x}\in \Omega:0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow f(\boldsymbol{x})>U)$$ このとき、 $$\lim_{\boldsymbol{x}\to \boldsymbol{a}}f(\boldsymbol{x})=\infty$$ と書く。
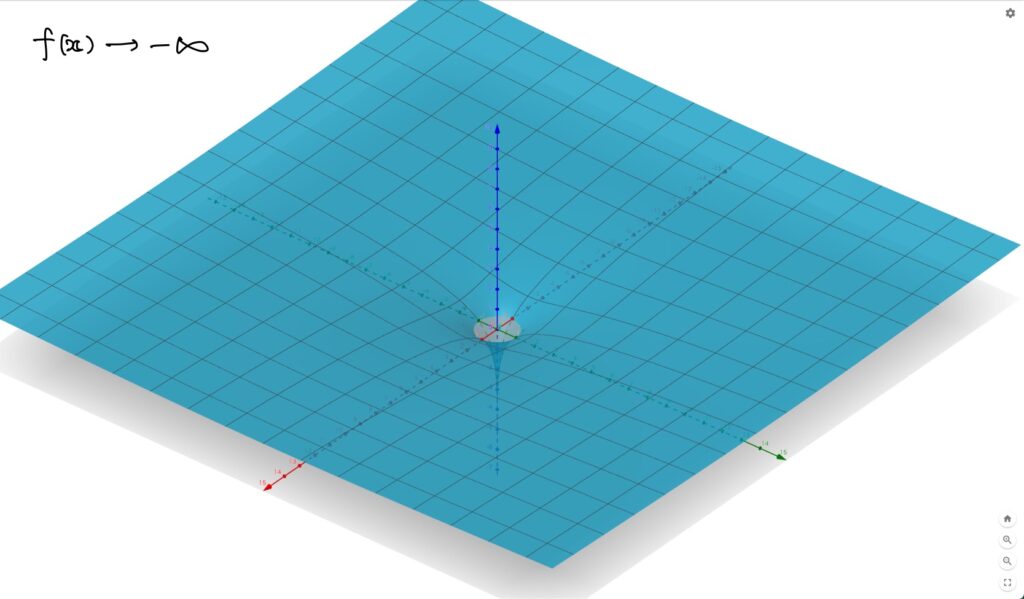
- ある点付近での\(\infty\)への発散 関数\(f\)が\(\boldsymbol{x}\to\boldsymbol{a}\)のとき\(-\infty\)(負の無限大)に発散するとは、次が成り立つことをいう。 $$(\forall L\in\mathbb{R})(\exists \delta>0)\ {\rm s.t.}\ (\forall\boldsymbol{x}\in\Omega:0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow f(\boldsymbol{x})<L)$$ このとき、 $$\lim_{\boldsymbol{x}\to\boldsymbol{a}}f(\boldsymbol{x})=-\infty$$ と書く。

実際に証明してみよう!
簡単ではありますが、実際に証明してみます。
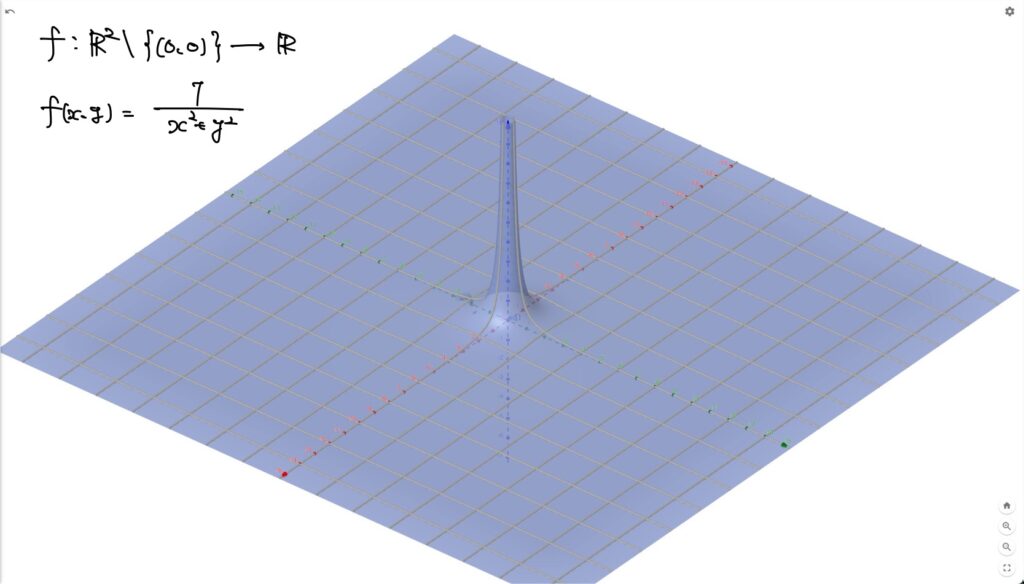
例1. \(\Omega=\mathbb{R}^2\setminus\{(0,0)\}\)とするとき、\(f:\Omega\to\mathbb{R}\)が\(\displaystyle f(x,y)=\frac{1}{x^2+y^2}\)で定められているとします。
このとき、\(\displaystyle\lim_{(x,y)\to(0,0)}\frac{1}{x^2+y^2}=\infty\)です。
証明
示したいことは
$$(\forall U\in\mathbb{R})(\exists \delta>0)\ {\rm s.t.}\ \left(\forall \boldsymbol{x}\in \Omega:0<\sqrt{x^2+y^2}<\delta\Rightarrow \frac{1}{x^2+y^2}>U\right)$$
です。
まず、任意の\((x,y)\in\Omega\)に対して\(\displaystyle\frac{1}{x^2+y^2}>0\)ですから、\(U>0\)のときを考えれば良いです。
任意の\(U>0\)に対して、\(\displaystyle\delta=\frac{1}{\sqrt{U}}\)とすれば、\(0<\sqrt{x^2+y^2}<\delta\)のとき
$$
\frac{1}{x^2+y^2}>\delta^2>\frac{1}{\left(\frac{1}{\sqrt{U}}\right)^2}=U
$$
となり、成り立ちます。
証明終わり
結
今回は\(\displaystyle\lim_{\boldsymbol{x}\to\boldsymbol{a}}f(\boldsymbol{x})=\pm\infty\)について解説しました。
結局の所1変数実数値関数のときとほぼ同じで、定義域内のある点に近づくとき、関数の値がどんな実数よりも大きければ正の無限大に発散、どんな実数よりも値避ければ負の無限大に発散という、というだけです。
次回は、発散する関数が絡む極限の式の証明をします。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする