本記事の内容
本記事は、多次元版ワイエルシュトラスの最大値定理と、そのために必要な点列の場合のボルツァーノ-ワイエルシュトラスの定理を証明する記事です。
本記事を読むにあたり、1変数実数値関数の場合のボルツァーノ-ワイエルシュトラスの証明、およびワイエルシュトラスの最大値定理の証明を知っている必要があるため、その際は以下の記事を参照してください。
多次元版ワイエルシュトラスの最大値定理のイメージのチャラい復習
多次元版ワイエルシュトラスの最大値定理のイメージを一言で述べれば、
ということでした。
例えば、次のような場合です。
例. Ω={x∈Rn∣|x|≤1}とし、f:Ω→Rがf(x,y)=x2+y2で定められているとします。
このfのグラフは次です。
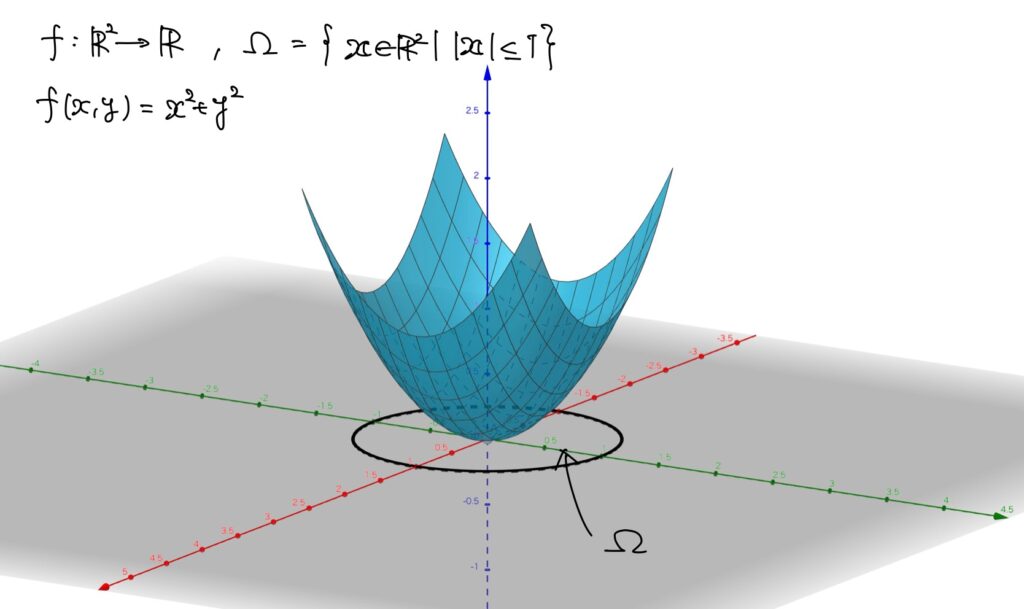
このとき、fはx2+y2=1を満たす(x,y)で最大値1を取ります。
つまり、(a,b)∈{(x,y)∈R2∣x2+y2=1}に対して、f(a,b)=1です。
一方、(x,y)=(0,0)で最小値0を取ります。
このように、定義域が閉集合で、かつ定義域で連続な多変数実数値関数は必ず最大値と最小値があります。
多次元版ワイエルシュトラスの最大値定理の明示
では、主張を明示しましょう。
形式的には１次元(１変数)の場合と何ら変わりません。
多次元版ワイエルシュトラスの最大値定理の証明の発想
証明のための発想は１通りではありませんので、ここでは筆者の発想について書くことにします。
結論から述べてしまえば、「１変数実数値関数のときと同じように証明できるんじゃないか？」と思ったわけです。
というもの、１変数実数値関数のときと本質的に主張は変わっていません。
単に定義域が区間から領域になっただけです。
勿論、定義域が区間から領域になることで何か問題が起こり、１変数実数値関数と同じように証明できない可能性もあります。
ただ、それは実際に証明してみないとわかりません。
つまり、「１変数の場合と本質的な主張は変わっていないのだから、多変数の場合も同様に証明ができるのではないか？もしできなかったら、そのときに別の方法を考えてみよう。」とういことです。
１変数の場合の証明の流れを参考にすれば、多次元版ワイエルシュトラスの最大値定理は次の流れで証明できそうです。
- (ステップ1)：f(x)が有界であることを示す。
1変数のときは、これを示すためにボルツァーノ-ワイエルシュトラスの定理を使った。 - (ステップ2)：f(x)が有界なのだから、上限が存在するため、その上限がf(K)の要素であることを示す。
上限がf(K)の要素であれば、その上限が最大値である。
ということです。
では、まずは点列の場合のボルツァーノ-ワイエルシュトラスの定理を証明してみましょう。
点列の場合のボルツァーノ-ワイエルシュトラスの定理
まずは、点列における有界について明示します。
数列と同じ感じですね。
では点列の場合のボルツァーノ-ワイエルシュトラスの定理の主張を明示しましょう。
{an}n∈NがRmの有界な点列であるとする。 このとき、Rmで収束するような{an}n∈Nの部分列が存在する。
定理2.の証明
任意のn∈Nに対して、
an=(an,1an,2⋮an,m)
と書いたとします。
このとき、各数列{an,1}n∈N, {an,2}n∈N,…,{an,m}n∈Nは有界な数列です。
実際、{an}n∈Nが有界な点列ですので、
(∃R∈R) (∀n∈N) |an|≤R
が成り立っています。
従って、あるR∈Rが存在して、任意のn∈Nに対して
√(an,1)2+(an,m)2+⋯+(an,m)2≤R
です。
1≤i≤mを満たす任意のi∈Nに対して、(an,i)2≥0ですから、an,i≤Rでなければなりません。
従って、各数列{an,1}n∈N, {an,2}n∈N,…,{an,m}n∈Nは有界な数列です。
従って、１次元のボルツァーノ-ワイエルシュトラスの定理が使えます。
この定理の証明は「ボルツァーノ-ワイエルシュトラスの定理を証明しよう！」【解析学の基礎シリーズ】を参照してください。
さて、定理3.から各数列{an,1}n∈N, {an,2}n∈N,…,{an,m}n∈Nには収束する部分列が存在します。
つまり、{ank(1),1}k(1)∈N, {ank(2),2}k(2)∈N,…,{ank(m),m}k(m)∈Nが存在して、これらは全て収束します。
このとき、これらがそれぞれa1, a2,…,am∈Rに収束するとしましょう。
すなわち、
(∀i∈N:1≤i≤m)limk(i)→∞ank(i),i=ai
としましょう。
ここで注意なのが、{ank(1),1}k(1)∈N, {ank(2),2}k(2)∈N,…,{ank(m),m}k(m)∈Nの添字の狭義単調増加自然数列{nk}k∈Nは1≤i≤mを満たす任意のi∈Nに対して、必ずしも一致しないということです。
さて、点列{an}n∈Nの部分列{ankl}l∈Nを考えます。
このとき、{ankl}l∈Nの各成分{ankl,1}l∈N, {ankl,2}l∈N,…,{ankl,m}l∈Nは収束する数列{ank,1}k∈N, {ank,2}k∈N,…,{ank,m}k∈Nの部分列ですのでa1, a2,…,amに収束します(この事実の証明は【解析学の基礎シリーズ】関数の極限編 その16を御覧ください)。
しかも1≤i≤mを満たす任意のi∈Nに対して添字の数列{nkl}l∈Nは全て一致しています。
従って、
liml→∞ankl=liml→∞(ankl,1ankl,2⋮ankl,m)=(a1a2⋮am)
{ankl}l∈Nは{an}n∈Nの部分列であり、かつ収束することが証明できたので、定理2.が成り立ちます。
定理2.の証明おわり
多次元の有界な集合
簡単にではありますが、多次元における有界な集合を説明します。
といっても、「有界な集合とはこれです。」というだけに留めます。
多次元版ワイエルシュトラスの最大値定理の証明の準備
多次元版ワイエルシュトラスの最大値定理の証明の流れを再掲すると、
- (ステップ1)：f(x)が有界であることを示す。
これを示すためにボルツァーノ-ワイエルシュトラスの定理を使う。 - (ステップ2)：f(x)が有界なのだから、上限が存在するため、その上限がf(K)の要素であることを示す。
上限がf(K)の要素であれば、その上限が最大値である。
でした。
この節では(ステップ1)で必要になる事実を証明します。
これを示すために次の2つを示します。
- fはaで連続である。
- aに収束するΩ内の任意の点列{xn}n∈Nに対して、limn→∞f(xn)=f(a)である。
命題5.の証明
1.⇒2.については、【解析学の基礎シリーズ】関数の極限編 その14の補題の証明に、「点列の極限はその成分の数列の極限を並べたベクトルと等しい」という事実を使えば証明できます。
2.⇒1.について示します。
背理法で示します。
仮に2.は成り立つが、1.が成り立たないと仮定しましょう。
すると、
(∃ϵ>0) s.t. (∀δ>0)(∃x∈Ω:0<|x−a|<δ∧f(x)−f(a)|≥ϵ)
です。
任意のn∈Nに対してδ=1nとおくと、点列{xn}n∈N⊂Ωに対して
|xn−a|<1n,|f(xn)−f(a)|≥ϵ
というϵ>0を見つけることができます。
すると、
xn→a,f(xn)↛f(a)(n→∞)
となりますが、これは2.に反します。
従って、2.⇒1.です。
命題5.の証明終わり
- Aは有界閉集合である、
- Aの要素からなる任意の点列{xn}n∈Nは収束する部分列を持ち、その極限はAに属する。
命題6.の証明
(1.⇒2.)の証明
Aが有界閉集合だとします。
また、{xn}n∈NをA内の任意の点列とします。
Aは有界ですので、{xn}n∈Nも有界です。
従って、多次元版のボルツァーノ-ワイエルシュトラスの定理から収束する部分列{xnk}k∈Nが存在します。
その収束先をaとします。
Aは閉集合ですので、次の事実を使います。
- KはRnの閉集合である。
- K内の任意の点列{an}n∈Nに対して、{an}n∈Nが(Rnで)収束するならば、その極限はKに属する。 言い換えれば、 (∀{an}n∈N∈K) anがRnで収束する。⇒limn→∞an∈Kが成り立つ。
命題7.の証明は【解析学の基礎シリーズ】多変数関数編 その17を参照してください。
命題7.により、a∈Aです。
(2.⇒1.)の証明
まずはAが有界であることを示します。
背理法で証明します。
仮にAが有界でないとしましょう。
すると、|xn|>nを満たすA内の点列{xn}n∈Nが取れます。
しかし、この点列はどんな収束する部分列も含みえません。
これは矛盾です。
従って、Aは有界です。
次にAが閉集合であることを示します。
A内の点列{xn}n∈Nがaに収束するとします。
このときaは必ずAに含まれる、ということを示します。
仮定から、部分列{xnk}n∈Nとa′∈Aが存在して、limk→∞xn=a′です。
ここで、limk→∞xn=aです。
従って、a=a′です。
故にa∈Aです。
命題6.の証明おわり
では、補題4.を証明します。
補題4.の証明
{yn}n∈Nをf(K)内の任意の点列とします。
このとき、任意のn∈Nに対して、f(xn)=ynであるようなK内の点列{xn}n∈Nが取れます(fは写像だから、任意のyn∈f(K)に対してyn=f(xn)というxnが存在します)。
命題6.の1.⇒2.により、あるa∈Kが存在して、limk→∞xnk=aを満たすような{xn}n∈Nの部分列{xnk}n∈Nが存在します。
fはKで連続な関数ですので、命題5.の1.⇒2.により、
limk→∞ynk=limk→∞f(xnk)=f(limk→∞xnk)=f(a)
です。
ちなみに、{yn}n∈Nは、K内の点f(a)に収束する{yn}n∈Nの部分列です。
命題6.の2.⇒1.により、f(K)はRmの有界閉集合です。
補題4.の証明おわり
結局何がしたかったのかネ？
結局何がしたかったのか、というとf(x)が有界であることを示すために必要な事実を述べた、ということです。
いざ、多次元版ワイエルシュトラスの最大値定理の証明
多次元版のワイエルシュトラスの最大値定理を再掲します。
いやぁ、長かったですね。
しかし、個々まで来てしまえばもうほんの一息です。
頑張りましょう！
定理1.(多次元版ワイエルシュトラスの最大値定理)の証明
(ステップ１)：f(x)が有界であることを示す。
これはつまり、f(K)が有界な集合であることを示すことになります。
Kが空集合でなはい集合ですので、f(K)も空集合ではありません。
また、Kが有界な閉集合で、かつf:K→RがKで連続である、という仮定から補題4.が使えます。
今回は補題4.のm=1の場合です。
従って、補題4.から、f(K)はRnの有界な閉集合です。
(ステップ2)：f(x)が有界なのだから、上限が存在するため、その上限がf(K)の要素であることを示す。
(ステップ2)の言い方を変えれば次です。
補題7.の証明
これは簡単です。
下に有界である場合も全く同じように証明できるため、上に有界のとき最大値が存在することを示します。
I⊂Rが空でなく、上に有界であるとします。
Iは上に有界ですので、Iには上限Sが存在します。
このSがIの要素であれば、証明が終わります。
上限は以下でした。
- SはAの上界である。すなわち、次が成り立つ。∀x∈A x≤S
- Sよりも小さい数はAの上界ではない。すなわち、次が成り立つ。 (∀ϵ>0)(∃x∈A) s.t. x>S−ϵ
詳しくは、上に有界、上界、上限」「下に有界、下界、下限」【解析の基礎シリーズ】を御覧ください。
上記の上限の条件のϵ>0は任意なので、任意のn∈Nを用いてϵ=1nとしても成り立ちます。
故に、
(∃xn∈I) s.t. S−1n≤xn≤S
です。
つまり、上記を満たすようなI内の数列{xn}n∈Nを見つけてこれる、という話です。
このとき、limn→∞xn=Sです。
実際、任意のϵ>0を用いて、1N<ϵというようなN∈Nを選んだ(アルキメデスの原理！)とします。
今、SはIの上限ですので、0≥S−xn<1nです。
従って、任意のϵ>0としたとき、n≥Nを満たす任意のn∈Nに対して、
|S−xn|=S−xn<1n<1N<ϵ
です。
従って、limn→∞xn=S
一方、Iは閉集合ですので、命題7.から、S∈Iです。
補題7.の証明終わり
では定理1.の証明に戻ります。
(ステップ1)により、f(K)は空集合でなく、Rnの有界な閉集合だということが分かりました。
故に補題7.から最大値が存在します。
定理1.(多次元版ワイエルシュトラスの最大値定理)の証明終わり
結
今回は点列の場合のボルツァーノ-ワイエルシュトラスの定理と多次元版ワイエルシュトラスの最大値定理を証明しました。
かなり長丁場になってしまいましたが、細分化することで徐々に証明できます。
次回は関数が極限を持つとき、定義域を制限した関数も同じ極限を持つ、ということを示します。
乞うご期待！質問、コメントなどお待ちしております！
コメントをする