「多変数多項式関数は連続な関数」【解析学の基礎シリーズ】多変数関数編その12

本記事の内容
多変数多項式関数とは何かネ？
$n$ 変数多項式関数は $\mathbb{R}^n$ で連続である
本当に成り立つのかネ？
結

本記事の内容

本記事は多変数多項式関数は連続な関数だ、ということを説明する記事です。

本記事を読むにあたり、多変数関数の連続について知っている必要があるため、その際は以下の記事を参照してください。

また、１変数多項式関数の連続について知っているとよりすんなり理解できると思われますので、その際は以下の記事を参照してください。

まずは、多変数多項式関数とはどんなものか、ということについて説明します。
では行きましょう！

多変数多項式関数とは何かネ？

多変数多項式関数の説明の前に、１変数多項式関数とは何だったかをチャラく復習します。

１変数多項式関数のチャラい復習

1変数多項式関数は $f(x)=x^2+2x+2$ のような形の関数のことを指したのでした。
数学的には以下でした。

多項式、多項式関数

多項式

$P(x)=\sum_{i=0}^{n}a_ix^i\quad (a_i\in\mathbb{R})$

$x$

実係数多項式

多項式関数

$f:X\to Y$

$x\in X$

$f(x)=P(x)$

$f$

多項式関数

$P(x)$

$f$

多変数多項式関数は上記の多変数ver.です。

多変数の多項式

$P(x,y)=x^2+2xy+3y^2+4x+5y+6$ のように、変数 $x,y$ と実数の定数から掛け算、足し算だけで作られる式を、変数 $x$ と $y$ の実係数多項式と言います。
これは2変数の場合です。
2変数の場合を数学的に表すと、 $x$ と $y$ の２変数実係数多項式は
$P(x,y)=\sum_{i=0}^N\sum_{j=0}^Na_{ij}x^iy^j\quad (N\in\mathbb{N},\ a_{ij}\in\mathbb{R})$
です。

では、多変数の多項式について説明します。
とはいえ、先程は $x$ と $y$ が変数でしたが、その変数の部分が $x_1,x_2,\dots, x_n$ となるだけです。

多変数の多項式

$P(x_1,x_2,\dots,x_n)=\sum_{i_1=0}^N\sum_{i_2=0}^N\dots\sum_{i_n=0}^Na_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}\quad (N\in\mathbb{N},\ a_{i_1i_2\cdots i_n}\in\mathbb{R})$ を変数

$x_1,x_2,\dots,x_n$ の多変数実係数多項式という。また、多変数実係数多項式の全体の集合を

$\mathbb{R}[x_1,x_2,\dots,x_n]=\left\{ P(x_1,x_2,\dots,x_n)\middle| N\in\mathbb{N},\ a_{i_1i_2\cdots i_n}\in\mathbb{R}\ (0\leq i_1,i_2,\dots,i_n\leq N)\right\}$ で表す。

数式にすると少々複雑に見えるかもしれませんが、 $n=2$ の場合を考えてみると、 $P(x,y)$ と一致することがわかると思います。

余談(読み飛ばしてOK)

実は、 $\mathbb{R}[x_1,x_2,\dots,x_n]$ は環の構造が入るので、 $\mathbb{R}[x_1,x_2,\dots,x_n]$ は多項式環とも呼ばれます。
環というのは、サラッと言うと「加減乗ができる集合」のことです。
割り算はできません( $0$ も多項式だからネ)。

多変数多項式関数

多変数多項式関数は、要するに、 $\mathbb{R}[x_1,x_2,\dots,x_n]$ の要素の形の関数のことです。
これを数学的に書くと次です。

多変数の多項式関数

$f$ が

$n$ 変数の(

$\mathbb{R}$ 上の)多項式関数であるとは、ある

$P(x_1,x_2,\dots,x_n)\in\mathbb{R}[x_1,x_2,\dots,x_n]$ が存在して、

$f:\mathbb{R}^n\to\mathbb{R},\quad f(x_1,x_2,\dots,x_n)=P(x_1,x_2,\dots,x_n)\quad ((x_1,x_2,\dots,x_n)^\top\in\mathbb{R}^n)$ であることを言う。

要するに、 $f:\mathbb{R}^n\to\mathbb{R}$ が
$f(x_1,x_2,\dots,x_n)=\sum_{i_1=0}^N\sum_{i_2=0}^N\dots\sum_{i_n=0}^Na_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}\quad (N\in\mathbb{N},\ a_{i_1i_2\cdots i_n}\in\mathbb{R})$
というときに、 $f$ は $x_1,x_2,\dots,x_n$ を変数とする $n$ 変数(実係数)多項式関数という、というわけです。

若干複雑ですが、 $n$ 変数多項式関数がどんなグラフかの例を挙げます。

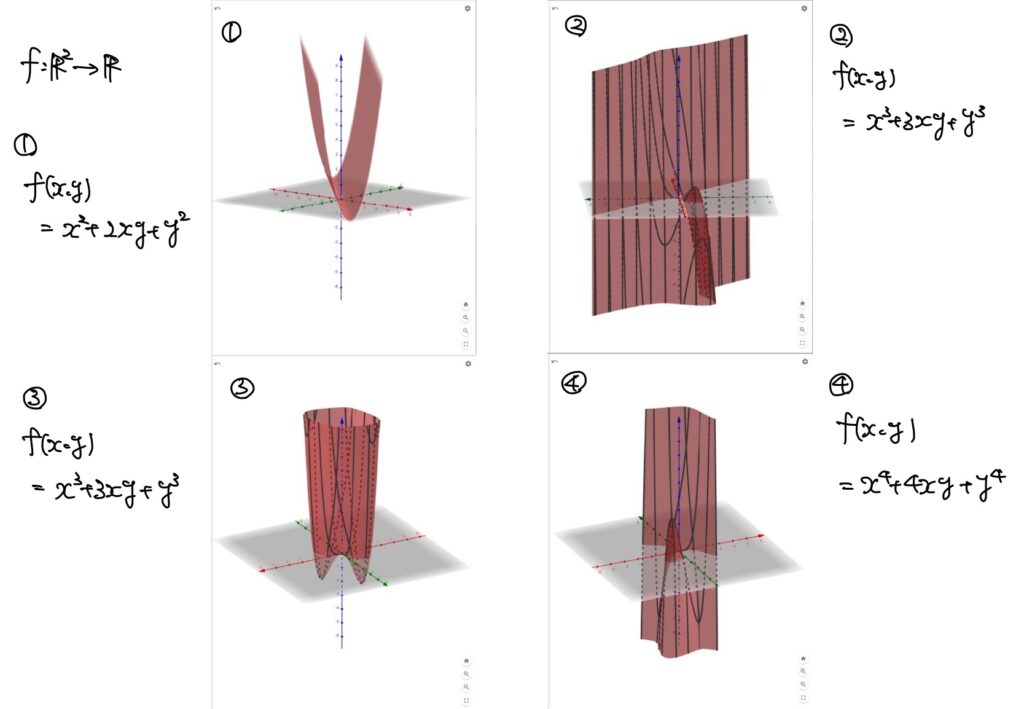
$n$ 変数多項式関数は $\mathbb{R}^n$ で連続である

$n$ 変数多項式関数は $\mathbb{R}^n$ で連続な関数です。
実は、今まで証明した、

(定理1.) 連続な多変数実数値関数の和、差も連続な関数。
(定理2.) 連続な多変数実数値関数の積も連続な関数。
(命題3.) $f_i(x_1,x_2,\cdots x_n)=x_i$ は連続な関数。(後でちゃんと書きます。)
(命題4.) 多変数の定数関数は連続な関数。

という事実を繰り返し使うことで直ちに証明できます。
(※1変数のときと同じだネ)

すなわち、

定理1.(多変数実数値関数の和・差の極限)

$\Omega\subset\mathbb{R}^n$ を

$\mathbb{R}^n$ の領域、

$f:\Omega\to\mathbb{R}$ および

$g:\Omega\to\mathbb{R}$ を写像(関数)、

$\boldsymbol{a}\in\bar{\Omega}$ とする。また、

$f$ と

$g$ は

$\Omega$ で連続だとする。このとき、

$f(\boldsymbol{x})\pm g(\boldsymbol{x})$ も

$\Omega$ で連続である。すなわち、

$(\forall \boldsymbol{a}\in\Omega)\ \displaystyle\lim_{\boldsymbol{x}\to\boldsymbol{a}}f(\boldsymbol{x})\pm g(\boldsymbol{x})=\left(\lim_{\boldsymbol{x}\to\boldsymbol{a}}f(\boldsymbol{x})\right)\pm\left(\lim_{\boldsymbol{x}\to\boldsymbol{a}}g(\boldsymbol{x})\right)=f(\boldsymbol{a})\pm g(\boldsymbol{a})$ が成り立つ。

(この定理の証明は【解析学の基礎シリーズ】多変数関数編その3を御覧ください)と

定理2.(多変数実数値関数の積の極限)

$\Omega\subset\mathbb{R}^n$ を

$\mathbb{R}^n$ の領域、

$f:\Omega\to\mathbb{R}$ および

$g:\Omega\to\mathbb{R}$ を写像(関数)、

$\boldsymbol{a}\in\bar{\Omega}$ とする。また、

$f$ と

$g$ は

$\Omega$ で連続だとする。このとき、

$f(\boldsymbol{x})\cdot g(\boldsymbol{x})$ も

$\Omega$ で連続である。すなわち、

$(\forall \boldsymbol{a}\in\Omega)\ \displaystyle\lim_{\boldsymbol{x}\to\boldsymbol{a}}f(\boldsymbol{x})\cdot g(\boldsymbol{x})=\left(\lim_{\boldsymbol{x}\to\boldsymbol{a}}f(\boldsymbol{x})\right)\cdot\left(\lim_{\boldsymbol{x}\to\boldsymbol{a}}g(\boldsymbol{x})\right)=f(\boldsymbol{a})\cdot g(\boldsymbol{a})$ が成り立つ。

(この定理の証明は【解析学の基礎シリーズ】多変数関数編その4を御覧ください)と命題3.(後述)と命題4.(後述)を繰り返し使うことで分かります。

では、定理を明示します。

定理5.

$n$ 変数実数係数多項式関数は

$\mathbb{R}^n$ で連続な関数である。

では、証明に入りましょう！

定理5.の証明

示したいことは $f:\mathbb{R}^n\to\mathbb{R}$ が
$f(x_1,x_2,\dots,x_n)=\sum_{i_1=0}^N\sum_{i_2=0}^N\dots\sum_{i_n=0}^Na_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}\quad (N\in\mathbb{N},\ a_{i_1i_2\cdots i_n}\in\mathbb{R})$
としたときに、 $f$ が $\mathbb{R}^n$ で連続なことです。

まずは、次を示します。

命題3.

$\Omega\subset\mathbb{R}^n$ を

$\mathbb{R}^n$ の領域とする。

$\boldsymbol{x}=(x_1,x_2,\dots,x_n)$ に対して、

$\boldsymbol{f}:\Omega\to\mathbb{R}$ が

$\boldsymbol{f}(\boldsymbol{x})=\left(f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\cdots,f_n(\boldsymbol{x})\right)$ と書いたとき

$f_i(\boldsymbol{x})=x_i$ で定められているとする。このとき、任意の

$1\leq i\leq n$ に対して、

$f_i(\boldsymbol{x})$ は

$\Omega$ で連続である。

命題4.の証明

示したいことは、 $\boldsymbol{x}=(x_1,x_2,\dots,x_n)$ 、 $\boldsymbol{a}=(a_1,a_2,\dots,a_n)$ としたとき、

$(\forall i\in\mathbb{N}:1\leq i\leq n)(\forall \epsilon_i>0)(\exists \delta_i>0)\ {\rm s.t.}\ (\forall\boldsymbol{x}\in\Omega;\ 0<|\boldsymbol{x}-\boldsymbol{a}|<\delta_i\Rightarrow |x_i-a_i|<\epsilon_i)$

です。
これは簡単です。
もし仮に、上記のような $\delta_i>0$ があったとすると、
$|\boldsymbol{x}-\boldsymbol{a}|<\delta_i\Leftrightarrow \sqrt{(x_1-a_1)^2+(x_2-a_2)^2+\cdots+(x_n-a_n)^2}<\delta_i$
です。
任意の $1\leq j\leq n$ を満たす $j\in\mathbb{N}$ に対して、 $(x_j-a_j)^2\geq 0$ ですので、任意の $1\leq j\leq n$ を満たす $j\in\mathbb{N}$ に対して $|x_j-a_j|<\delta_i$ です。
従って、 $\delta_i=\epsilon_i$ とすると、任意の $1\leq j\leq n$ を満たす $j\in\mathbb{N}$ に対して、
$|\boldsymbol{x}-\boldsymbol{a}|<\delta_i\Rightarrow |x_j-a_j|<\epsilon_i$
となりますので、証明完了です。

命題4.の証明終わり

次に、多変数の定数関数も $\mathbb{R}^n$ で連続であることを示します。

命題4.(多変数の定数関数は連続な関数)

$\Omega\subset\mathbb{R}^n$ を

$\mathbb{R}^n$ の領域とする。

$c\in\mathbb{R}$ とし、

$\boldsymbol{x}=(x_1,x_2,\dots,x_n)$ に対して、

$f:\Omega\to\mathbb{R}$ が

$f(\boldsymbol{x})=c$ で定められているとする。このとき、

$f(\boldsymbol{x})$ は

$\Omega$ で連続である。

命題4.の証明

示したいことは、
$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall\boldsymbol{x}\in\Omega;\ 0<|c-c|<\delta_i\Rightarrow |c-c|<\epsilon)$
ですが、これは $\delta=\epsilon$ とすることで、
$0<|c-c|<\delta_i\Rightarrow |c-c|=0<\epsilon_i$
です。
故に証明は終わりです。

命題4.の証明終わり

さて、定理5.の証明に戻ります。

命題4.から $g:\mathbb{R}^n\to\mathbb{R}$ が $g(\boldsymbol{x})=c$ で定められている(すなわち、 $g$ は定数関数)とき、 $g$ は $\mathbb{R}^2$ で連続です。
また、命題3.から $h:\mathbb{R}^n\to\mathbb{R}$ が $h(x_1.x_2,\cdots,x_n)=x_i$ で定められているとします。
このとき $h$ は $\mathbb{R}^2$ で連続です。
ここで、定理2.から $g(\boldsymbol{x})h(\boldsymbol{x}=cx_i)$ も $\mathbb{R}^n$ で連続です。

ここで、更に定理2.を繰り返し使うことで、任意の $0\leq i_1,i_2,\cdots ,i_n\leq N\ (N\in\mathbb{N})$ を満たす $i_1,i_2,\cdots ,i_n\in\mathbb{Z}$ に対して、
$a_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}\quad (a_{i_1i_2\cdots i_n}\in\mathbb{R})$
は $\mathbb{R}^n$ で連続です。

加えて、ここで定理1.により、 $0\leq i_1,i_2,\cdots ,i_n\leq N$ の $i_1,i_2,\cdots ,i_n$ を $i_j\ (1\leq j\leq n)$ それぞれに対して $0$ から $N$ までの和を取っても $\mathbb{R}^n$ で連続です。

以上のことから、
$\sum_{i_1=0}^N\sum_{i_2=0}^N\dots\sum_{i_n=0}^Na_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}\quad (N\in\mathbb{N},\ a_{i_1i_2\cdots i_n}\in\mathbb{R})$
は $\mathbb{R}^n$ で連続です。

本当に成り立つのかネ？

成り立ちます。
簡単ですが、例を挙げましょう。

例1. $f:\mathbb{R}^2\to\mathbb{R}$ が $f(x,y)=x^2+2xy+y^2$ で定められているとします。
このとき $f$ は $\mathbb{R}^2$ で連続です。

証明

示したいことは、 $\boldsymbol{a}=(a,b)$ と書いたとき、
$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall\boldsymbol{x}\in\Omega;\ 0<|(x,y)-(a,b)|<\delta\Rightarrow \left|(x^2+2xy+y^2)-(a^2+2ab+b^2)\right|<\epsilon)$
です。

$\delta>0$ を見つけるために式変形してみましょう。
$\begin{eqnarray} \left|(x^2+2xy+y^2)-(a^2+2ab+b^2)\right|&=&\left| x^2-2ax+a^2+y^2-2by+b^2+2ax-2a^2+2by-2b^2 \right|\\ &=&\left| (x-a)^2+(y-b)^2+2a(x-a)+2b(y-b) \right|\\ &\leq&|x-a|^2+|y-b|^2+2|a|\cdot|x-a|+2|b|\cdot|y-b| \end{eqnarray}$
です。
仮に、上記を満たす $\delta$ があったとすると、 $0<|(x,y)-(a,b)|<\delta\Leftrightarrow \sqrt{(x-a)^2+(y-b)^2}<\delta$ であり、 $(x-a)^2\geq0$ かつ $(y-b)^2\geq0$ ですので、 $|x-a|<\delta$ かつ $|y-b|<\delta$ です。
故に、
$\begin{eqnarray} |x-a|^2+|y-b|^2+2|a|\cdot|x-a|+2|b|\cdot|y-b|&<&\delta^2+\delta^2+2(|a|+|b|)\delta \end{eqnarray}$
です。
従って、 $\delta^2+\delta^2+2(|a|+|b|)\delta=\epsilon$ を満たす $\delta>0$ を見つけてくれば良いことになります。
故に、これを解くと、
$\delta=\frac{-(|a|+|b|)\pm\sqrt{(|a|+|b|)^2+2\epsilon}}{2}$
です。
従って、
$\delta=\frac{-(|a|+|b|)+\sqrt{(|a|+|b|)^2+2\epsilon}}{2}$
とすれば、 $\delta>0$ です。
$\displaystyle\delta=\frac{-(|a|+|b|)+\sqrt{(|a|+|b|)^2+2\epsilon}}{2}$ とすると、
$\begin{eqnarray} \left|(x^2+2xy+y^2)-(a^2+2ab+b^2)\right|&<&2\delta^2+2(|a|+|b|)\delta\\ &=&2\cdot \left( \frac{-(|a|+|b|)+\sqrt{(|a|+|b|)^2+2\epsilon}}{2}\right)^2\\ &\quad&+2(|a|+|b|)\cdot\frac{-(|a|+|b|)+\sqrt{(|a|+|b|)^2+2\epsilon}}{2}\\ &=&\frac{1}{2}\cdot \left( (|a|+|b|)^2-2(|a|+|b|)\sqrt{(|a|+|b|)^2+2\epsilon}\\ +(|a|+|b|)^2+2\epsilon\right)-(|a|+|b|)^2+\sqrt{(|a|+|b|)^2+2\epsilon}\\ &=&\epsilon \end{eqnarray}$
です。
従って、
$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall\boldsymbol{x}\in\Omega;\ 0<|(x,y)-(a,b)|<\delta\Rightarrow \left|(x^2+2xy+y^2)-(a^2+2ab+b^2)\right|<\epsilon)$
です。

証明終わり

結

今回は多変数の多項式関数が連続であることを説明しました。
結局の所、

連続な多変数実数値関数の和、差も連続な関数。
連続な多変数実数値関数の積も連続な関数。
$f_i(x_1,x_2,\cdots x_n)=x_i$ は連続な関数。
多変数の定数関数は連続な関数。

という事実を繰り返し使うことで証明ができるということでした。

次回は多変数の有理関数の連続について解説します。

乞うご期待！質問、コメントなどお待ちしております！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

本記事の内容

多変数多項式関数とは何かネ？

１変数多項式関数のチャラい復習

多変数の多項式

余談(読み飛ばしてOK)

多変数多項式関数

nn変数多項式関数はRn\mathbb{R}^nで連続である

定理5.の証明

命題4.の証明

命題4.の証明終わり

命題4.の証明

命題4.の証明終わり

本当に成り立つのかネ？

証明

証明終わり

結

コメントをする

$n$ 変数多項式関数は $\mathbb{R}^n$ で連続である