本記事の内容
本記事は、累次積分、すなわち多変数の積分について解説する記事です。
本記事を読むにあたり、積分とは何か、1変数の積分について知っている必要があるため、以下の記事も合わせてご覧ください。
※1変数の積分の記事が複数あるため、一部のリンクを貼っています。
↓「積分とは何か?」の記事
↓1変数の積分の記事
多変数の積分ってどうやって計算するんですか?
ここでは、多変数の積分の効果的な計算方法のイメージについて解説します。
1変数のときの軽い復習
そもそも積分は、リーマン和の極限として定められました。
具体的に関数が与えられたとき、その積分の値をこのリーマン和の極限に基づいて計算するというのは誠に骨が折れます。
なぜなら、「区間の分割を定めて〜、和を計算して〜、その極限が存在するかを議論して〜、極限が分割と代表点に依存しないことを示して〜」など色々議論しなければならないことが多いからです。
勿論、「この方法はだめだ」と言っているわけではなくて、本来はこのように積分を、すなわち極限を求めるのが正攻法です。
しかし、実際的ではないのです。
1変数関数の場合は以下の事実を使って計算しました。
定理1.(微分積分学の基本定理の系)
\(f\)を\(I=[a,b]\ (a<b)\)で連続な実数値関数とするとき、次の2つが成り立つ。- \(f\)の不定積分\(\displaystyle F(x)=\int_a^xf(y)\ dy\)は、\(I\)における\(f\)の原始関数である。
- \(I\)における\(f\)の任意の1つの原始関数\(G(x)\)は\(G(x)=F(x)+C\ \)(\(C\)は定数)の形で、基本公式 $$ \int_a^b f(x)\ dx=G(b)-G(a) $$ が成り立つ。また①の右辺を\(\left[ G(x)\right]_a^b\)と表す。
定理1.の証明は【解析学の基礎シリーズ】積分編 その15を御覧ください。
要するに、1変数の場合は定理1.に基づいて、\(f\)の原始関数を求めることによって積分の値が計算できます。
多変数の場合
では、多変数関数の積分を求めるために、定理1.と同様な効果的な方法はないでしょうか?
結論を言うと、あります。
その方法は、\(n\)次元の有界閉区間\(I=[a_1,b_1]\times[a_2,b_2]\times\dots\times[a_n,b_n]\)上で定められた可積分関数\(f(\boldsymbol{x})=f(x_1,x_2,\dots,x_n)\)の積分を
$$
\int_If(\boldsymbol{x})\ d\boldsymbol{x}=\int_{a_1}^{b_1}\left\{\int_{a_2}^{b_2}\left\{\cdots\left\{\int_{a_n}^{b_n}f(x_1,x_2,\dots,x_n)\ dx_n\right\}\cdots\right\}dx_2\right\}dx_1\cdots①
$$
のように各変数\(x_i\)についての積分を\(n\)回繰り返すことで得られます。
多変数の積分の幾何学的(図形的)イメージ
この式①が成り立つ条件については後述することにして、ここでは①が成り立ったときの\(n=2\)の場合について見ていきましょう。
添字があると面倒なので、\(x_1=x\)、\(x_2=y\)と書くことにして、\(I=[a,b]\times[c,d]\)とすると、①は
$$
\int_If(\boldsymbol{x})\ d\boldsymbol{x}=\int_{[a,b]\times[c,d]}f(\boldsymbol{x})\ d\boldsymbol{x}=\int_a^b\left\{\int_c^df(x,y)\ dy\right\}dx\cdots②
$$
となります。
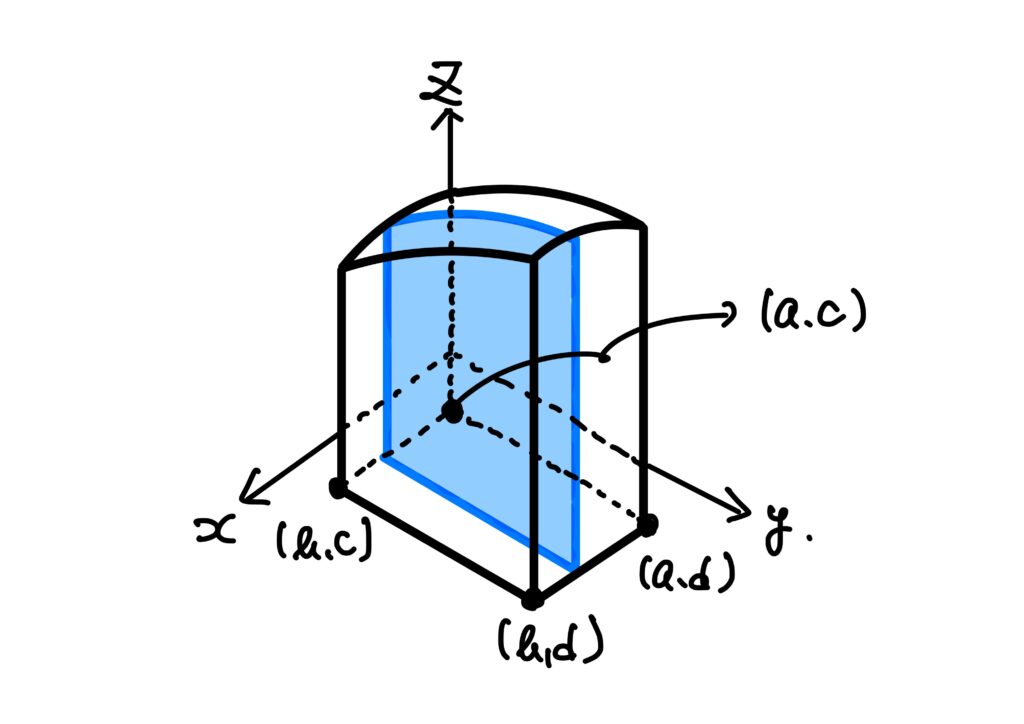
この場合、\(\displaystyle\int_If(\boldsymbol{x})\ d\boldsymbol{x}\)は、\(f\)のグラフ\(z=f(x,y)\)の下にある部分の体積を表します。
②は、この体積が、\(x=\)一定として得られる平面で、この体積を切った切り口の面積を表す
$$
\int_c^df(x,y)\ dy
$$
を\(x\)について積分したものに等しいことを表しています。
実際、\(\displaystyle\int_c^df(x,y)\ dy\)は、変数\(y\)についての積分ですので、この積分においては\(x\)は定数です。
\(x\)が定数ということは、「変化しない」ということです。
従って、先の図を真横から、すなわち\(x\)軸と垂直な方向から見ると
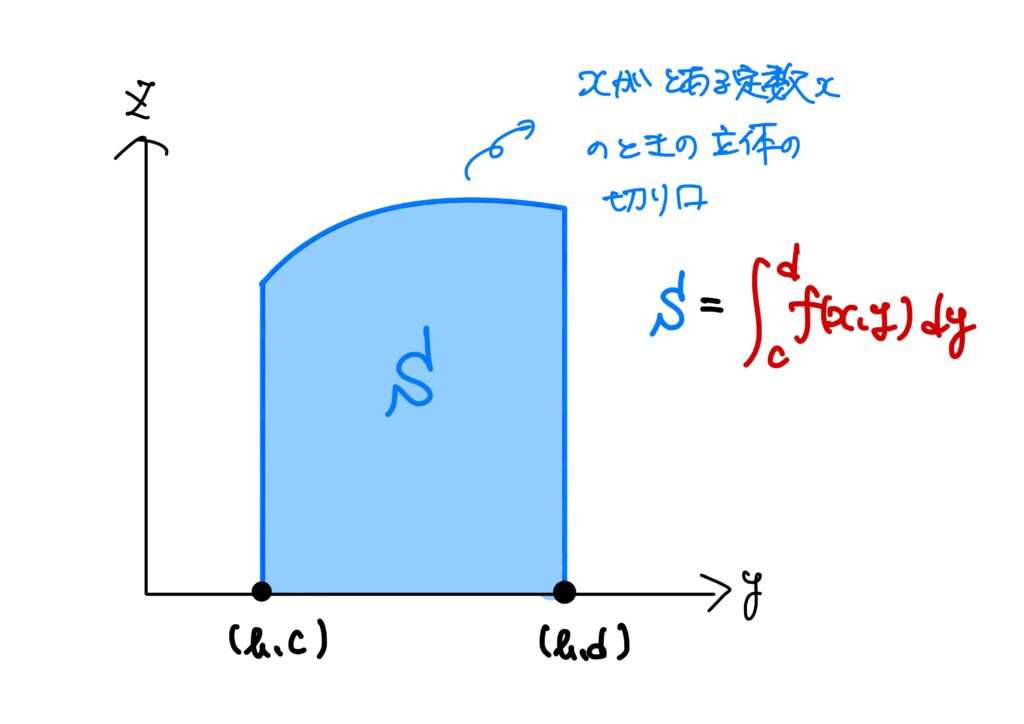
となるため、\(\displaystyle\int_c^df(x,y)\ dy\)は、\(x=\)一定のときで立体を切った切り口の面積を表しています。
さて、そもそも\(\displaystyle\int_If(\boldsymbol{x})\ d\boldsymbol{x}\)とは何だったかと言うと、
$$
\displaystyle\int_If(\boldsymbol{x})\ d\boldsymbol{x}=\lim_{d(\Delta)\to0}s\left(f;\Delta;\boldsymbol{\xi} \right)
$$
において、\(d(\Delta)\to0\)なる極限が、分割\(\Delta\)によって得られる各小区間\(I_k\)の\(y\)軸に平行な辺の中さをまず\(\to0\)として、次に\(x\)軸に平行な辺の長さを\(\to0\)とする極限に等しい、ということを意味しています。
要するに、どういうことですか?
「結構難しいな」と思ったかもしれませんが、よりサラッと図で説明します。
そもそも積分は小区間における体積の和でした。
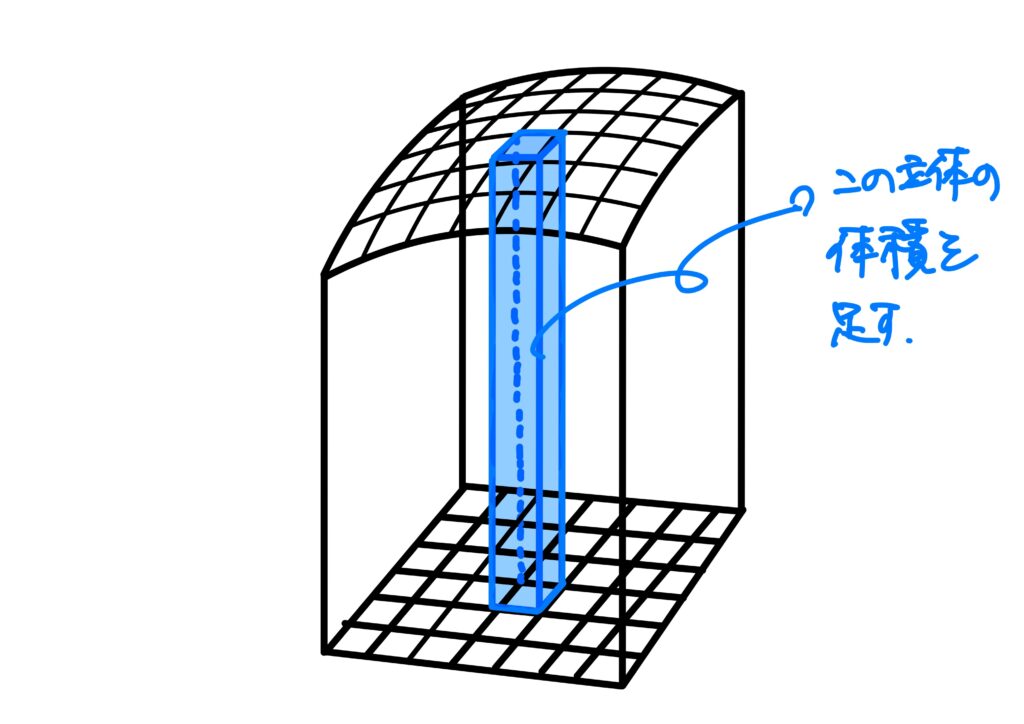
上記のように、小さい直方体の体積を足し合わせて、全体の立体の面積を求める、というのが元々の積分でした。
今回の方法を図で表すと以下です。
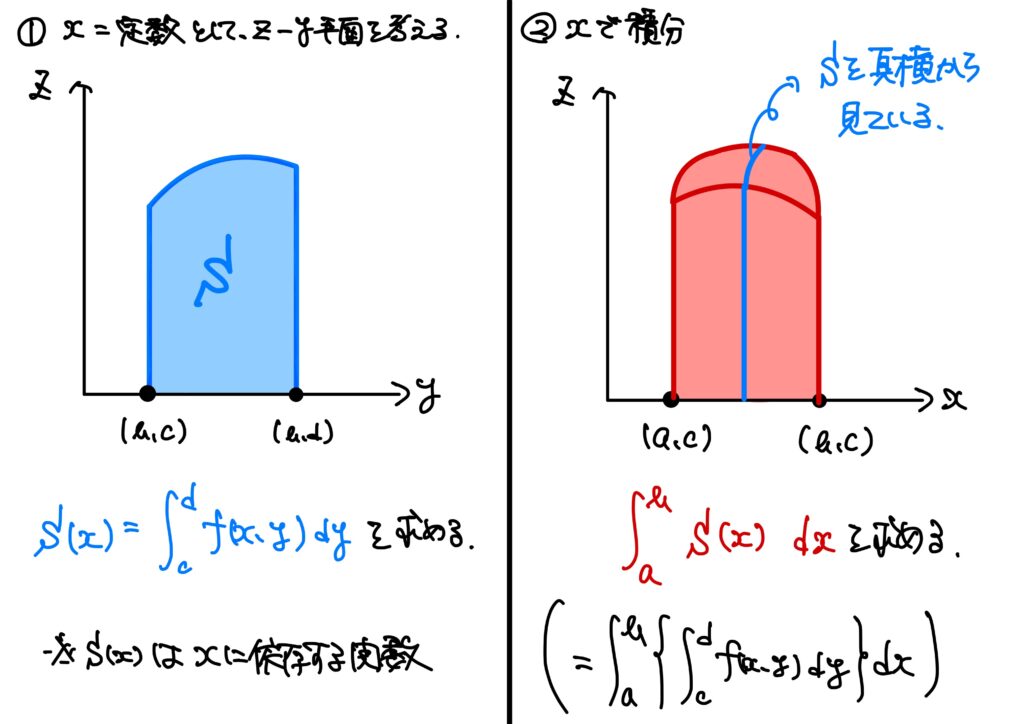
まず\(x\)を定数として立体の切り口の面積をを考えます。
その立体の切り口である平面の面積を\(x\)に依存する形で求め、次にその平面の面積を\(x\)軸方向に動かしたときの軌跡でもって元の立体を網羅して体積を求める、ということです。
一旦計算してみます。
イメージはつかめたと思いますが、結局の所、計算上は1変数の積分を繰り返すだけです。
それを例を挙げて実際に計算してみます。
例2. \(\displaystyle I=\int\int_{[0,a]\times[0,b]}\left( x^2+y^2\right)\ dxdy\)を計算してみます。
②により、
\begin{eqnarray}
I&=&\int_0^a\left\{\int_0^b\left( x^2+y^2\right)\ dy\right\}dx\\
&=&\int_0^a\left[ x^2y+\frac{1}{3}y^3\right]_{y=0}^{y=b}\ dx\\
&=&\int_0^a\left( bx^2+\frac{1}{3}b^3\right)\ dx\\
&=&\left[ \frac{1}{3}bx^3+\frac{1}{3}b^3x\right]_0^a\\
&=&\frac{ab}{3}\left(a^2+b^2 \right)
\end{eqnarray}
と計算できます。
要するに、「①が成り立つようなときは、今のように計算しましょうね」ということです。
記号のお話
①の証明についての基本的な部分は、\(n\)次元区間上の積分を低次元区間上の積分の繰り返し(累次積分)に置き換える点にあります。
そこで、\(n=p+q\)となる整数\(p,q\geq1\)を取り、\(n\)次元区間\(I=[a_1,b_1]\times[a_2,b_2]\times\dots\times[a_n,b_n]\)上の積分を\(p\)次元区間
$$J=[a_1,b_1]\times[a_2,b_2]\times\dots\times[a_p,b_p]$$
と\(q\)次元区間
$$K=[a_{p+1},b_{p+1}]\times[a_2,b_2]\times\dots\times[a_n,b_n]$$
上の積分に分解することを考えます。
このとき区間の体積は辺の長さの積なので、
$$
v(I)=v(J)\times v(K)\cdots③
$$
が成り立ちます。
今、\(\boldsymbol{z}=(z_1,z_2,\dots,z_n)\in\mathbb{R}^n\)に対して、
$$
\boldsymbol{x}=(z_1,x_2,\dots,z_p)\in\mathbb{R}^p,\quad \boldsymbol{y}=(z_{p+1},z_{p+2},\dots,z_n)\in\mathbb{R}^q
$$
として、\(\boldsymbol{z}=(\boldsymbol{x},\boldsymbol{y})\)と書くことにします。
さて、\(I\)の任意の分割\(\Delta\)は、\(I\)の\(n\)個の辺に有限個の分点を定めることにより与えられるので、\(I\)の分割は\(J\)と\(K\)の分割\(\Delta^\prime\)と\(\Delta^{\prime\prime}\)を与えることになります。
逆に、\(J,K\)の分割\(\Delta^\prime,\ \Delta^{\prime\prime}\)を任意に与えたとすると、それらの分点をあわせて\(I=J\times K\)の分割\(\Delta\)が得られます。
このとき、\(\Delta=\Delta^\prime\times\Delta^{\prime\prime}\)と書くことにします。
この場合、各\(k\in K(\Delta)\)に対して、\(I_k=J_l\times K_m\)、\(l\in K(\Delta^\prime)\)、\(m\in K(\Delta^{\prime\prime})\)のような形になるわけですので、\(k=(l,m)\)と書くことにすると
$$
K(\Delta)=K(\Delta^\prime)\times K(\Delta^{\prime\prime})
$$
となります。
本記事ではこのように記号を書くことにします。
①の証明に必要な事実の明示とその証明
では、①式が成り立つという主張を明示して証明します。
主張の明示
定理0.
有界な実数値関数\(f:I=J\times K\to\mathbb{R}\)が次の2つの条件1.、2.を満たすとする。- \(f\)は\(I\)上で可積分である。
- 各\(\boldsymbol{x}\in J\)を固定するとき、\(\boldsymbol{y}\)の関数\(f^\boldsymbol{x}: \boldsymbol{y}\mapsto f(\boldsymbol{x},\boldsymbol{y})\)は\(K\)上で可積分である。
主張の証明
少々長丁場です。
定理0.の証明
\(I\)の任意の分割\(\Delta=\Delta^\prime\times\Delta^{\prime\prime}\)を取り、小区間\(I_k=J_l\times K_m\ (k=(l,m)\in K(\Delta)=K(\Delta^\prime)\times K(\Delta^{\prime\prime}))\)上での\(f\)の上限、下限を\(M_k,\ m_k\)とします。
\(f\)に上限と下限が存在するのは\(f\)が有界だからです。
このとき、\(I_k\)の任意の点\(\boldsymbol{z}_k=(\boldsymbol{x}_k,\boldsymbol{y}_k)\)に対して、
$$
m_k\leq f(\boldsymbol{x}_k,\boldsymbol{y}_k)\leq M_k\cdots⑤
$$
が成り立ちます。
ここで、積分の区間に関する加法性を使います。
定理3.(区間に関する加法性)
\(\Delta\)を\(\mathbb{R}^n\)の有界閉集合\(I\)の任意の分割とし、\(f\)を\(I\)上の有界な関数とする。\(f\)が\(I\)上で可積分ならば、全ての\(k\in K(\Delta)\)に対し、\(f\)は\(I_k\)上で可積分で $$ \int_If(\boldsymbol{x})\ d\boldsymbol{x}=\sum_{k\in K(\Delta)}\int_{I_k}f(\boldsymbol{x})\ d\boldsymbol{x}\cdots① $$ が成り立つ。逆に、\(f\)が全ての\(I_k\ (k\in K(\Delta))\)上で可積分ならば、\(f\)は\(I\)上で可積分で①が成り立つ。定理3.の証明は【解析学の基礎シリーズ】積分編 その9を御覧ください。
定理3.と仮定2.により、関数\(f^\boldsymbol{x}:\boldsymbol{y}\mapsto f(\boldsymbol{x},\boldsymbol{y})\)は\(K_m\)上で可積分で、⑤から
$$
m_k\cdot v(K_m)\leq \int_{K_m}f(\boldsymbol{x},\boldsymbol{y})\ d\boldsymbol{y}\leq M_k\cdot v(K_m)\quad (\boldsymbol{x}\in J_l)
$$
です。
この式を\(m\in K(\Delta^{\prime\prime})\)について和を取ると、
$$
\sum_{m\in K(\Delta^{\prime\prime})}m_k\cdot v(K_m)\leq \sum_{m\in K(\Delta^{\prime\prime})}\int_{K_m}f(\boldsymbol{x},\boldsymbol{y})\ d\boldsymbol{y}=F(\boldsymbol{x})\leq \sum_{m\in K(\Delta^{\prime\prime})}M_k\cdot v(K_m)
$$
となります。
今、各\(J_l\)から点\(\boldsymbol{\xi}_l\)を選び、上の不等式で\(\boldsymbol{x}=\boldsymbol{\xi}_l\)としたものに\(v(J_l)\)を掛けて\(l\in K(\Delta^\prime)\)について和を取ると、③と同様に\(v(I_k)=v(J_l)\times v(K_m)\)だから、
$$
s_\Delta(f)=\sum_{k\in K(\Delta)}m_kv(I_k)\leq s\left(F;\Delta^\prime;\boldsymbol{\xi} \right)\leq\sum_{k\in K(\Delta)}M_kv(I_k)=S_\Delta(f)\cdots⑥
$$
が得られます。
ただし、\(s_\Delta\)と\(S_\Delta\)はそれぞれ不足和、過剰和です。
仮定1.により、\(f\)は可積分だから、\(d(\Delta)\to0\)としたとき、上の不等式の両端の辺は共に\(\displaystyle\int_If(\boldsymbol{z})\ d\boldsymbol{z}\)に収束します。
そして、
$$
\max\left\{d(\Delta^\prime),d(\Delta^{\prime\prime})\right\}\leq d(\Delta)\leq\sqrt{d(\Delta^\prime)^2+d(\Delta^{\prime\prime})^2}
$$
だから、\(d(\Delta)\to0\)は、\(d(\Delta^\prime)\to0\)かつ\(d(\Delta^{\prime\prime})\to0\)と同値です。
従って、
$$
\lim_{d(\Delta^\prime)\to0}s\left(F;\Delta^\prime;\boldsymbol{\xi} \right)=\int_If(\boldsymbol{z})\ d\boldsymbol{z}\cdots⑦
$$
が得られます。
これは、\(\displaystyle F(\boldsymbol{x})=\int_Kf(\boldsymbol{x},\boldsymbol{y})\ d\boldsymbol{y}\)が\(J\)上で可積分で、かつ④が成り立つということを示しています。
もう少々詳しく述べると、仮定1.により
$$
(\forall \epsilon>0)\ (\exists \delta>0)\ {\rm s.t.}\ \left(\forall \Delta\in\mathcal{D}(I)\right)\\
\left(d(\Delta)<\delta\Longrightarrow\left|s_\Delta-\int_If(\boldsymbol{z})\ d\boldsymbol{z}\right|<\frac{\varepsilon}{3},\ \left|S_\Delta-\int_If(\boldsymbol{z})\ d\boldsymbol{z}\right|<\frac{\varepsilon}{3}\right)
$$
が成り立ちます。
このとき、\(\displaystyle d(\Delta)<\frac{\delta}{2}\)を持たす\(J\)の任意の分割\(\Delta^\prime\)に対して、\(\displaystyle d(\Delta^{\prime\prime})<\frac{\delta}{2}\)となる\(K\)の分割\(\Delta^{\prime\prime}\)を一つ取り、\(\Delta=\Delta^\prime\times \Delta^{\prime\prime}\)となる\(I\)の分割\(\Delta\)を作れば、
$$
d(\Delta)\leq\sqrt{d(\Delta^\prime)^2+d(\Delta^{\prime\prime})^2}\leq\frac{\delta}{\sqrt{2}}<\delta
$$
だから、⑥により
\begin{eqnarray}
\left|s\left(F;\Delta^\prime;\boldsymbol{\xi}\right)-\int_If(\boldsymbol{z})\ d\boldsymbol{z} \right|&\leq&\left|s\left(F;\Delta^\prime;\boldsymbol{\xi}\right)-s_\Delta\right|+\left|s_\Delta-\int_If(\boldsymbol{z})\ d\boldsymbol{z}\right|\\
&\leq&\left|S_\Delta-s_\Delta\right|+\left|s_\Delta-\int_If(\boldsymbol{z})\ d\boldsymbol{z}\right|\\
&\leq&\left|S_\Delta-\int_If(\boldsymbol{z})\ d\boldsymbol{z}\right|+2\left|s_\Delta-\int_If(\boldsymbol{z})\ d\boldsymbol{z}\right|<\varepsilon
\end{eqnarray}
が成り立ちます。
これで⑦が証明されました。
定理0.の証明終わり
この定理0.のおかげで、多変数の場合の積分は定義域で分割して計算できるということが保証されます。
定理0.についてちょっとだけ踏み込んだお話
積分は、有限和の極限として定められている、と言いかえることもできます。
④に対応するものは、有限和では
$$
\sum_{\substack{1\leq i\leq m\\ 1\leq j\leq n}}a_{ij}=\sum_{i=1}^m\left\{\sum_{j=1}^na_{ij}\right\}\cdots⑧
$$
です。
すなわち、長方形状の格子点\(\left\{(i,j)\mid 1\leq i\leq m,\ 1\leq j\leq n\right\}\)についての総和である左辺が、縦の列の和\(\displaystyle\sum_{j=1}^na_{ij}\)の和として求められるのです。
この公式⑧は定理0.の証明でも⑥を得るところで使っています。
定理0.の2つの仮定のうち、本質的には1.が重要です。
ルベーグ・フビニの定理(「そういう定理があるんだあ」でOKです)によれば、仮定1.が成り立つ有界な関数\(f\)に対して、仮定2.はほとんどすべての\(\boldsymbol{x}\in J\)に対して成り立ちます。
少々詳しく言うと、次回定める零集合\(E\)が存在して、\(\boldsymbol{x}\not\in E\)のときに、\(\boldsymbol{y}\mapsto f(\boldsymbol{x},\boldsymbol{y})\)は\(K\)上で可積分となります。
そして、仮定1.のみで④が成り立つことが示されます。
皆様のコメントを下さい!
以前にもお話したかもしれませんが(してたらごめんなさい)、筆者が大学で数学を学んでいるときに「面白いなあ!」と思った瞬間は大きく分けて2つあります。
1つは、一見関係のなさそうな分野がつながるときです。
例えば、大学一年のときに解析の分野で線型代数が出現したときです。
「微分にも行列が絡んでくるんだあ」と思ったときです。
2つ目は中高で習ったことを厳密に語るときです。
例えば、極限の話です。
高校数学の教科書では(筆者のときは)「限りなく近づく」という表現で極限が説明されていました。
当時は「ふーん。そうなんだー。」と特に疑問はなかったのですが、よく考えてみると「”限りなく近づく”って何?」という話です。
それを厳密に説明されたときには、難しかったですが同時に面白いと思いました。
皆様はどうですか?
筆者と同じ感覚をお持ちの方はいらっしゃいますか?是非コメントで教えて下さい!
結
今回は、累次積分、多変数の積分の計算方法について解説しました。
今回示した定理0.により、多変数の積分は定義域で分割して計算することが出来ることが保証されます。
次回は、今回証明した定理0.から得られる系として、積分する順序の話をします。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!




コメントをする