本記事の内容
本記事は「上に有界、上界、上限」および「下に有界、下界、下限」について説明する記事です。
本記事は実数の連続性と関連がありますので、もしよろしければ、以下の記事も参照してください。
上に有界、上界、上限
例6.
区間\([0,1]=\{x\in \mathbb{R}\mid 0<x\leq 1\}\)は\(\mathbb{R}\)の部分集合であり、かつ\([0,1]\)の全ての要素は\(1\)以下です。
例7.
区間\((2,3)=\{x\in \mathbb{R}\mid 2<x<3\}\)は\(\mathbb{R}\)の部分集合であり、かつ\((2,3)\)の全ての要素は\(3\)より小さいです。
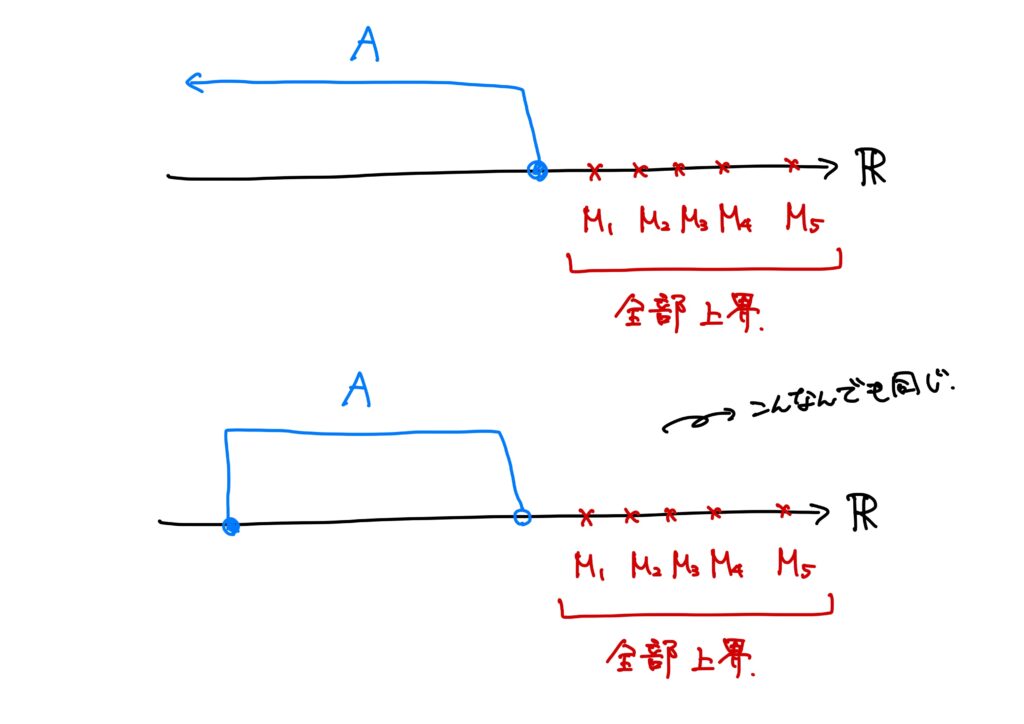
このように、\(\mathbb{R}\)の部分集合に対して、その部分集合のどんな元よりも大きいか等しい実数が存在するときに、その実数のことを上界(a upper bound)といいます。
要は、「ある実数の部分集合がとある実数を超えることはありませんよ」というその”とある実数”のことを上界と呼ぶというわけです。
これを論理式で書けば、次です。
例6および例7について再度言及すると、例6については\(1\)以上であれば\(5\)も\(7\)も\(300\)も\([0,1]\)の上界だし、上に有界です。
例7については\(3\)以上であれば\(100\)も\(183\)も\(100000\)も\((2,3)\)の上界ですし、上に有界です。
ポイントとしては、\(A\subset \mathbb{R}\)が空集合でなく、かつ上に有界であれば、上界は無限個存在します。
さらにこのとき、上界には必ず最小値が存在するということです。
ちなみに、例6では\(1\)が、例7では\(3\)が上界の最小値です。
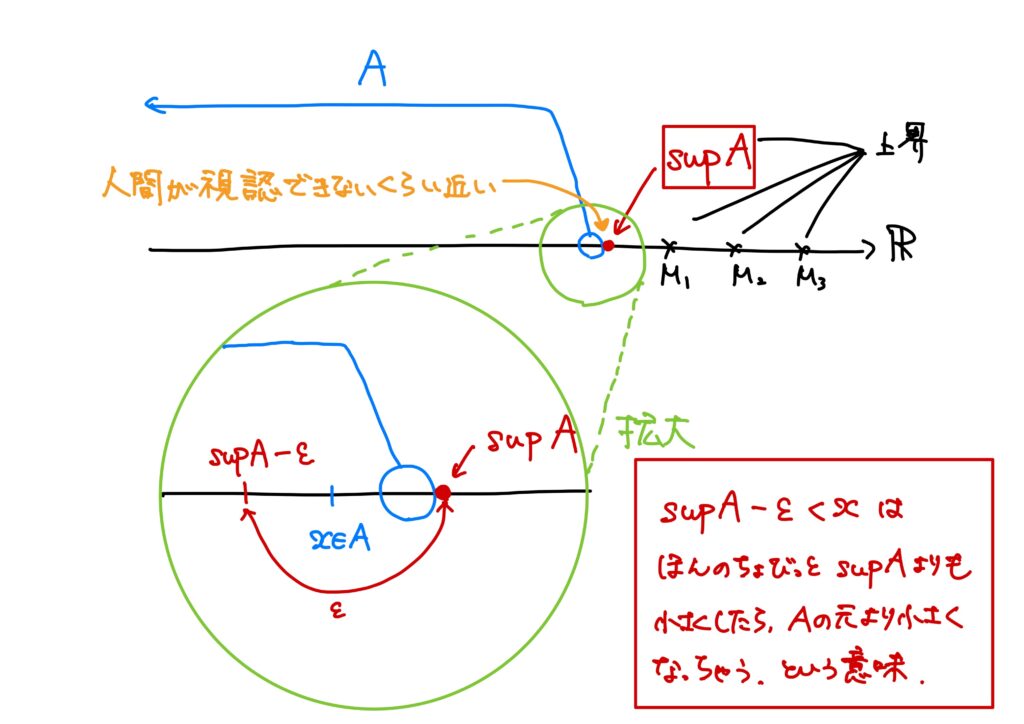
この上界の最小値のことを上限(supremum)といいます。
言い方を変えると、「上界の中で、その上界よりも”ほんのちょっとでも”小さい実数はもう上界ではないという上界」のことを上限というのです。
「むしろわからん」となるかもしれないので、図を参照してください。
この上限を論理式で書くと、
- \(S\)は\(A\)の上界である。すなわち、次が成り立つ。$$\forall x\in A\ x\leq S$$
- \(S\)よりも小さい数は\(A\)の上界ではない。すなわち、次が成り立つ。 $$(\forall \epsilon>0)(\exists x\in A)\ {\rm s.t.}\ x>S-\epsilon$$
2.が「”ほんのちょっとでも”小さい実数はもう上界ではない」に対応します。
\(\epsilon\)は正であればどんな実数でも良いので、めちゃくちゃ小さくても良いのです。
平たく言えば、「遠目に見たらほぼ0じゃね?という実数でも良い」ということです。
よって、\(S-\epsilon\)は「\(S\)よりも”ほんのちょっとでも”小さい実数」に対応し、\(x>S-\epsilon\)は、「そんな実数は上界じゃないぜ」ということに対応します。
下に有界、下界、下限
上界、上限に対応する概念として、「下界(”げかい”ではなく”かかい”)」、「下限」もあります。
これは上界、上限の条件の不等式を逆にしたものであって、上界、上限が分かればなんてことはありません。
例6.
区間\([0,1]=\{x\in \mathbb{R}\mid 0<x\leq 1\}\)は\(\mathbb{R}\)の部分集合であり、かつ\([0,1]\)の全ての要素は\(0\)以上です。
例7.
区間\((2,3)=\{x\in \mathbb{R}\mid 2<x<3\}\)は\(\mathbb{R}\)の部分集合であり、かつ\((2,3)\)の全ての要素は\(2\)より大きいです。
このように、\(\mathbb{R}\)の部分集合に対して、その部分集合のどんな元よりも小さいか等しい実数が存在するときに、その実数のことを下界(かかい)(a lower bound)といいます。
要は、「ある実数の部分集合がとある実数よりも小さいなんてことはありませんよ」というその”とある実数”のことを下界と呼ぶというわけです。
これを論理式で書けば、次です。

例6および例7について再度言及すると、例6については\(0\)以下であれば\(-5\)も\(-7\)も\(-300\)も\([0,1]\)の下界ですし、下に有界です。
例7については\(2\)以下であれば\(-11\)も\(-183\)も\(-100000\)も\((2,3)\)の下界ですし、下に有界です。
ポイントとしては、\(A\subset \mathbb{R}\)が空集合でなく、かつ下に有界であれば、下界は無限個存在します。
さらに、このとき下界には必ず最大値が存在するということです(上界の場合は最小値が存在するのでした)。
ちなみに、例6では\(0\)が、例7では\(2\)が下界の最大値です。
この下界の最大値のことを下限(infimum)といいます。
言い方を変えると、「下界の中で、その下界よりも”ほんのちょっとでも”大きい実数はもう下界ではないという下界」のことを下限というのです。
「むしろわからん」となるかもしれないので、図を参照してください。

下限を論理式で書くと、次です。
- \(I\)は\(A\)の下界である。すなわち、次が成り立つ。$$\forall x\in A\ I\leq x$$
- \(I\)よりも大きい数は\(A\)の下界ではない。すなわち、次が成り立つ。 $$(\forall \epsilon>0)(\exists x\in A)\ {\rm s.t.}\ I+\epsilon>x$$
2.が「”ほんのちょっとでも”大きい実数はもう下界ではない」に対応します。
\(\epsilon\)は正であればどんな実数でも良いので、めちゃくちゃ小さくても良いです。
平たく言えば、「遠目に見たらほぼ0じゃね?という実数でも良い」ということです。
よって、\(I+\epsilon\)は「\(I\)よりも”ほんのちょっとでも”大きい実数」に対応し、\(I+\epsilon>x\)は、「そんな実数は下界じゃないぜ」ということに対応します。
結
今回は「上に有界、上界、上限」および「下に有界、下界、下限」について説明しました。
次回は、「上限と最大値、下限と最小値は違うの?」です。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする
大変わかりやすいです。ありがとうございます。
1つよろしければ質問させてください。
「上界には必ず最小値が存在する」
「下界には必ず最大値が存在する」
の証明はどのようなものなのでしょうか?
shelly様
コメントありがとうございます。
また、大変鋭いご指摘、ありがとうございます。
お答えいたします。
>大変わかりやすいです。ありがとうございます。
こちらこそ、ありがとうございます。大変励みになります。
>「上界には必ず最小値が存在する」「下界には必ず最大値が存在する」の証明はどのようなものなのでしょうか?
まず、ご質問の意図が「上限(および下限)は分かった。その性質として“上限は上界の最小値である(下限は下界の最大値である)”という性質も分かった。しかし、上限(下限)という概念を知らない立場において“上界(下界)の集合に最小値(最大値)が存在する”ということの証明はどうか。」というものでしたら、再度お問い合わせ下さい。
今回のお問い合わせでは、「上限は上界の中で最小のものである」という主張を証明します(下限については上限と本質的に同じなので省略いたします)。
結論から申し上げますと、以下のワイエルシュトラスの上限公理から従います。
ワイエルシュトラスの上限公理
\(A\subset\mathbb{R}\)、\(A\neq\emptyset\)、\(A\)は上に有界であるとする。このとき、\(A\)の上限\(\sup A\)が存在する。すなわち、上に有界かつ空でない\(\mathbb{R}\)の任意の部分集合は上限を持つ。
(ワイエルシュトラスの上限公理の詳細は実数の連続性編 その6を御覧ください)
確かに記事中では、例を使って
$$
U(A)=\left\{M\in\mathbb{R}\middle|(\forall x\in A)\ x\leq M \right\}
$$
とするとき、\(U(A)\)には最小値が存在し、その最小値を\(A\)の上限(supremum of \(A\))と呼び、\(\sup A\)で表す。
というような表現で上限(および下限)を説明致しました。
しかし、上限(および下限)を定める際には「最小値(下限のときは最大値)」という言葉は使っておりません。
何が言いたいかといえば、
という立場で記事を書いているということです。
本記事では、デデキントの定理(実数の連続性編 その2)とワイエルシュトラスの上限公理の同値性を証明していますので、ワイエルシュトラスの上限公理は「正しい」と断言できます。
そこで、ここでは
命題
\(A\subset\mathbb{R}\)、\(A\neq\emptyset\)、\(A\)は上に有界であるとする。このとき、\(A\)の上限\(\sup A\)が存在し、\(\sup A\)は\(A\)の上界のうち最小のものと一致する。
を証明します。
証明
これは、ワイエルシュトラスの上限公理そのものであり、ワイエルシュトラスの上限公理はデデキントの定理から従うため、割愛します。
(※「デデキントの定理\(\Longrightarrow\)ワイエルシュトラスの上限公理」の証明は実数の連続性編 その5を御覧ください。
背理法で証明します(上限が、上界の中で最小のものでないと仮定して矛盾を導きます)。
空でない\(A\subset\mathbb{R}\)の上限\(\sup A\)を\(\alpha\)と書いたとします。
すなわち、\(\alpha=\sup A\)とします。
ここで、\(A\)の上限とは以下でした。
上限
\(A\subset\mathbb{R}\)、\(A\neq\emptyset\)、\(M\in\mathbb{R}\)とする。このとき、
すなわち、次が成り立つ。
$$
(\forall x\in A)\ x\leq M
$$
すなわち、以下が成り立つ。
$$
(\forall \varepsilon>0)(\exists x\in A)\ {\rm s.t.}\ x>M-\varepsilon
$$
を満たすならば、\(M\)を\(A\)の上限(supremum of \(A\))といい、\(M=\sup A\)と書く。ただし、\(A\)が上に有界でないならば、\(\sup A=\infty\)と書く。
さて、証明に戻ります。
\(\alpha=\sup A\)ですから、\(\alpha\)は\(A\)の上界です。
すなわち、
$$
(\forall x\in A)\ x\leq \alpha
$$
です。
仮に、\(\alpha\)が上界の中で最小値でないとします。
「そもそも、最小値とは何だったか?」というと以下でした。
最小値
\(A\subset\mathbb{R}\)とするとき、\(I\in\mathbb{R}\)が\(A\)の最小値であるとは
が成り立つことをいう。
今回は、「\(\alpha\)は\(A\)の上界の集合\(U(A)\)の最小値でない。」という仮定ですので、上記の否定が成り立ってます。
すなわち、
が成り立っています。
しかしながら、「\(\alpha\)は\(A\)の上界である」ということは仮定ですので、今回の場合は
$$
(\exists \alpha^\prime\in U(A))\ {\rm s.t.}\ \alpha^\prime<\alpha
$$
が成り立っているということになります
とどのつまり、\(\alpha\)を\(A\)の上界の中で最小のものでないと仮定すれば、\(A\)の上界であり、かつ\(\alpha\)より小さい\(\alpha^\prime\in\mathbb{R}\)が存在するとわかる、ということです。
まとめれば、
を同時に満たす\(\alpha^\prime\in\mathbb{R}\)が存在するということです。
しかしながら、これは
$$
(\forall \varepsilon>0)(\exists x\in A)\ {\rm s.t.}\ x>\alpha-\varepsilon
$$
に反します。
したがって、\(\alpha\)は上界の集合\(U(A)\)の最小値です。