本記事の内容
本記事はコーシー列の例を挙げ、それを証明する記事です。
また、「コーシー列とは何か」ということを数学的に説明します。
本記事を読むにあたり、コーシー列のイメージを知っているとより分かりやすいと思われますので、以下の記事も合わせて御覧ください。
コーシー列ってどんなの?
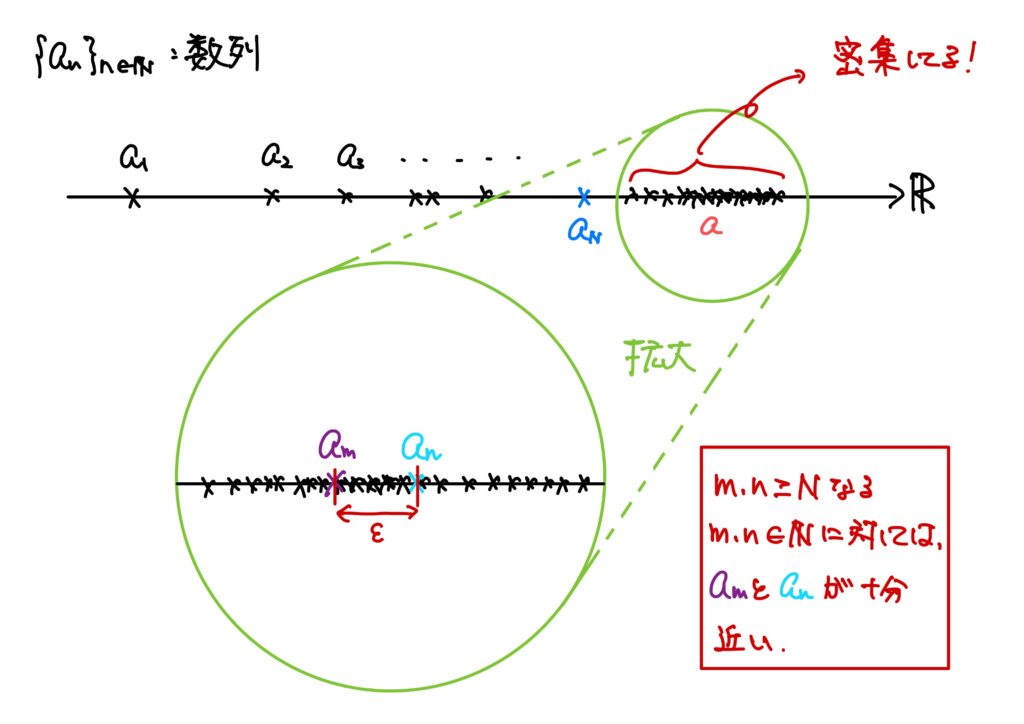
前回の記事で、コーシー列は
という発想から来ていると述べました。
つまり、
という条件を満たす数列がコーシー列なのです。
ネタバラシしておくと、実数の範囲では収束列であれば、必ずコーシー列です。
例1.
\(\displaystyle a_n=1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{n^2}\)とします。
この数列はコーシー列です。
つまり、ある番号以降の\(a_n\)の値同士は十分近です。
ちなみに、この数列の項をいくつか具体的に書いてみると、次です。
- \(a_1=1\),
- \(a_2=\displaystyle1+\frac{1}{4}=1.25\),
- \(\displaystyle a_2=1+\frac{1}{4}+\frac{1}{9}=1.361111111\dots\),
- \(\displaystyle a_5=1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}=1.463611111\dots\),
- \(\displaystyle a_{10}=1+\frac{1}{4}+\dots+\frac{1}{100}=1.54976773116654\dots\),
- \(\displaystyle a_{100}=1+\frac{1}{4}+\dots+\frac{1}{10000}=1.643498390018489\dots\).
およそ収束するとは思えないのですが(筆者の主観だけどね)、これは上に有界な単調増加数列なので収束します(「有界な単調列は収束する。」という命題の証明は【解析学の基礎シリーズ】実数の連続性編 その9を御覧ください)。
さて、これがコーシー列であることを示しましょう。
アルキメデスの原理から、任意の正の実数\(\epsilon\)に対して、ある自然数\(N\)が存在して、\(1<N\epsilon\)を満たします。
従って、\(\displaystyle\frac{1}{N}<\epsilon\)を満たします。
自然数\(m,n\)が\(m\geq N\)を満たしていたとします。
さらに、先程見つけた自然数\(N\)について、\(m,n\geq N\)を満たしていたとします。
すなわち、\(m\geq n\geq N\)であるとします。
このとき、数列\(\{a_n\}_{n\in\mathbb{N}}\)は単調増加数列であることを用いれば、
\begin{eqnarray}
0\leq a_m-a_n&=&1+\frac{1}{2^2}+\cdots+\frac{1}{m^2}-1-\frac{1}{2^2}-\cdots-\frac{1}{n^2}\\
&=&\frac{1}{(n+1)^2}+\frac{1}{(n+2)^2}+\cdots+\frac{1}{m^2}
\end{eqnarray}
となります。
また、分数において、分母が小さい数の方が大きいので、
\begin{eqnarray}
&&\frac{1}{(n+1)^2}+\frac{1}{(n+2)^2}+\cdots+\frac{1}{m^2}\\
&\leq&\frac{1}{n(n+1)}+\frac{1}{(n+1)(n+2)}+\cdots+\frac{1}{(m-1)m}
\end{eqnarray}
となります。
ここで、部分分数分解(口に出して言うと毎回噛む。ぶぶんぶんぶんぶんとか言っちゃう。)を使うと、
\begin{eqnarray}
&&\frac{1}{n(n+1)}+\frac{1}{(n+1)(n+2)}+\cdots+\frac{1}{(m-1)m}\\
&=&\left(\frac{1}{n}-\frac{1}{n+1}\right)+\left(\frac{1}{n+1}-\frac{1}{n+2}\right)+\cdots+\left(\frac{1}{m-1}-\frac{1}{m}\right)\\
&=&\frac{1}{n}-\frac{1}{m}\leq\frac{1}{n}\leq\frac{1}{N}<\epsilon
\end{eqnarray}
となります。
\(\epsilon\)は任意の正の実数だったので、\(a_m-a_n<\epsilon\)が成り立ったのだから、\(a_m\)と\(a_n\)は十分近いです。
従って、数列\(\{a_n\}_{n\in\mathbb{N}}\)はコーシー列です。
ちなみに、この数列は\(\displaystyle\frac{\pi^2}{6}=1.64493406684\cdots\)に収束することはLeonhard Euler(レオンハルト・オイラー)が証明しました。
気になった方は「バーゼル問題」を見てみると良いと思います。
で、コーシー列って?
コーシー列は
という条件を満たす数列のことだと述べました。
これを論理式で表すと次です。
\(\{a_n\}_{n\in\mathbb{N}}\)を数列とする。このとき、\(\{a_n\}_{n\in\mathbb{N}}\)がコーシー列であるとは、 $$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall m,n\in\mathbb{N}\ m,n\geq N\Rightarrow |a_m-a_n|<\epsilon)$$ が成り立つことをいう。
結
今回は、「コーシー列とは何か」ということを明示しつつ、その例を挙げて証明を与えました。
実は、実数の範囲では「ある数列が収束列である。\(\Rightarrow\)ある数列がコーシー列である。」なのです。
これをコーシーの収束条件と呼ぶこともあります。
少々ネタバラシしておくと、コーシー列は収束する、ということを証明するためにボルツァーノ-ワイエルシュトラスの定理を使います。
次回は「収束列ならばコーシー列である。」ことの証明を与えます。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする