「$f^\prime>0$($<0$)ならば狭義単調増加(減少)」「$f^\prime=0$と定数関数は同値」【解析学の基礎シリーズ】1変数実数値関数の微分編 その9

本記事の内容

本記事は「微分係数が正(負)ならば狭義単調増加(減少)関数である。」と「微分係数が$0$であることと定数関数であることは同値」という事実を証明する記事です。

本記事を読むにあたり、平均値の定理について知っている必要があるため、以下の記事も合わせて御覧ください。

「平均値の定理を証明しよう！」【解析学の基礎シリーズ】１変数実数値関数の微分編 その８

...

for-spring.com

2022.06.24

高校のときを思い出してみよう

「高校のときを思い出してみよう」とは言ったものの「修学旅行楽しかったなあ」とかそういう思い出を思い出してほしいわけではなくて、高校数学を思い出してほしいという意味です(わかってるわ！というツッコミが来そうですが)。
もちろん、楽しかったなあという思い出は大事です。
たまーに思い出しますよね。

そんな話は置いておいて、高校数学で学んだけれど、イメージで納得していただけで厳密に証明を与えていない事実があります。
それが、「ある点の微分係数の符号によって、その点で増加しているか減少しているかかがわかる」という話です。

イメージでいうと以下のような感じです。

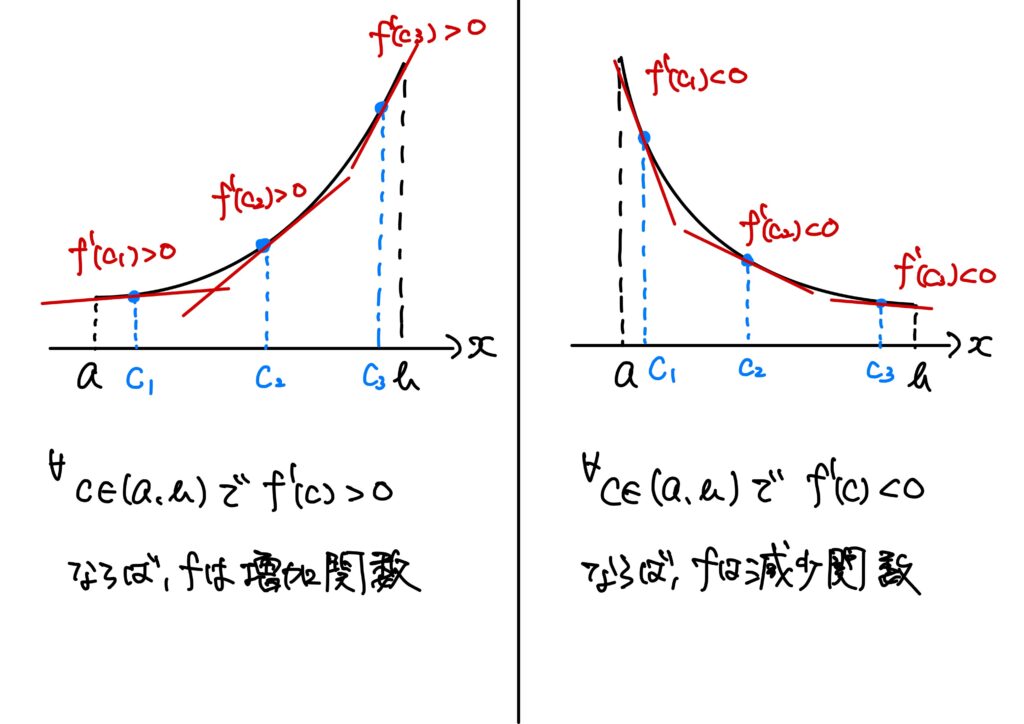
高校生の筆者は「そりゃそうじゃね？」と思っていましたし、証明についてはほんの少しも考えたこともありませんでした。
しかしながら、大学に入学して数学を学んでいると「証明しないことには正しいとは言えない」ということを学びました。

とどのつまり、この記事では「高校数学でイメージで納得していた事実を厳密に証明してみましょう」ということです。

微分係数が正ならば狭義単調増加関数

平たくいえば、「微分係数が正であれば狭義単調増加関数」という主張です。
これを数学的に厳密に書くと次になります。

この定理の証明には平均値の定理を使います。
平均値の定理は何だったか、というと、以下でした。

平均値の定理の証明は【解析学の基礎シリーズ】1変数実数値関数の微分編 その8を御覧ください。

定理1.の証明

簡単です。もう、一瞬です。

$f:[a,b]\to\mathbb{R}$が連続で、$(a,b)$で微分可能、任意の$c\in(a,b)$に対して$f^\prime(c)>0$だとします。

$f:[a,b]\to\mathbb{R}$が連続で、$(a,b)$で微分可能ですので、$x_1<x_2$を満たす$x_1,x_2\in(a,b)$に対して、$(x_1,x_2)$でも$f$は連続かつ微分可能です。
故に平均値の定理から
$$(\exists c_0\in(x_1,x_2))\ {\rm s.t.}\ \frac{f(x_2)-f(x_1)}{x_2-x_1}=f^\prime(c_0)$$
です。
仮定から任意の$c\in(a,b)$に対して$f^\prime(c)>0$ですので、$c_0\in(x_1,x_2)\subset(a,b)$でも$f^\prime(c_0)>0$です。
故に、
$$\frac{f(x_2)-f(x_1)}{x_2-x_1}>0$$
です。
ここで、$x_1<x_2$ですので、$x_2-x_1>0$です。
従って、$f(x_2)-f(x_1)>0$、すなわち、$f(x_1)>f(x_1)$です。

以上のことから、$f$は狭義単調増加関数です。

定理1.の証明終わり

次に微分係数が負であれば狭義単調減少関数だ、という事実を証明します。

微分係数が負ならば狭義単調減少関数

微分係数が正のときと同様に、「微分係数が負ならば狭義単調減少関数である」という主張を数学的に書けば次です。

定理2.の証明

定理1.と同じですので読み飛ばしてもOKです。

$f:[a,b]\to\mathbb{R}$が連続で、$(a,b)$で微分可能、任意の$c\in(a,b)$に対して$f^\prime(c)<0$だとします。

$f:[a,b]\to\mathbb{R}$が連続で、$(a,b)$で微分可能ですので、$x_1<x_2$を満たす$x_1,x_2\in(a,b)$に対して、$(x_1,x_2)$でも$f$は連続かつ微分可能です。
故に平均値の定理から
$$(\exists c_0\in(x_1,x_2))\ {\rm s.t.}\ \frac{f(x_2)-f(x_1)}{x_2-x_1}=f^\prime(c_0)$$
です。
仮定から任意の$c\in(a,b)$に対して$f^\prime(c)<0$ですので、$c_0\in(x_1,x_2)\subset(a,b)$でも$f^\prime(c_0)<0$です。
故に、
$$\frac{f(x_2)-f(x_1)}{x_2-x_1}<0$$
です。
ここで、$x_1<x_2$ですので、$x_2-x_1>0$です。
従って、$f(x_2)-f(x_1)<0$、すなわち、$f(x_1)<f(x_1)$です。

以上のことから、$f$は狭義単調減少関数です。

定理2.の証明終わり

上記の定理に微分係数が$0$のときの場合も含めれば、単調増加(減少)関数だという主張になります。

微分係数が非負(非正)ならば単調増加(減少)関数

この主張を数学的に書くと次です。

定理3.の証明

これも定理1.および定理2.と同じなので読み飛ばしてOKです。

$f:[a,b]\to\mathbb{R}$が連続で、$(a,b)$で微分可能、任意の$c\in(a,b)$に対して$f^\prime(c)>0$だとします。

$f:[a,b]\to\mathbb{R}$が連続で、$(a,b)$で微分可能ですので、$x_1<x_2$を満たす$x_1,x_2\in(a,b)$に対して、$(x_1,x_2)$でも$f$は連続かつ微分可能です。
故に平均値の定理から
$$(\exists c_0\in(x_1,x_2))\ {\rm s.t.}\ \frac{f(x_2)-f(x_1)}{x_2-x_1}=f^\prime(c_0)$$
です。

①$f^\prime(c)\geq0$の場合
任意の$c\in(a,b)$に対して$f^\prime(c)\geq0$とします。
このとき、$c_0\in(x_1,x_2)\subset(a,b)$でも$f^\prime(c_0)\geq0$です。
故に、
$$\frac{f(x_2)-f(x_1)}{x_2-x_1}\geq0$$
です。
ここで、$x_1<x_2$ですので、$x_2-x_1>0$です。
従って、$f(x_2)-f(x_1)\geq0$、すなわち、$f(x_1)\geq f(x_1)$です。

以上のことから、$f$は単調増加関数です。

②$f^\prime(c)\leq0$の場合
任意の$c\in(a,b)$に対して$f^\prime(c)\leq0$とします。
このとき、$c_0\in(x_1,x_2)\subset(a,b)$でも$f^\prime(c_0)\leq0$です。
故に、
$$\frac{f(x_2)-f(x_1)}{x_2-x_1}\leq0$$
です。
ここで、$x_1<x_2$ですので、$x_2-x_1>0$です。
従って、$f(x_2)-f(x_1)\leq0$、すなわち、$f(x_1)\leq f(x_1)$です。

以上のことから、$f$は単調減少関数です。

定理3.の証明終わり

最後に、「微分係数が$0$であることと定数関数であることは同値」という主張を証明します。

微分係数が$0$であることと定数関数であることは同値

「微分係数が$0$であることと定数関数であることは同値」という主張を数学的に書くと次です。

この定理の証明も簡単です。

定理4.の証明

$f:[a,b]\to\mathbb{R}$が連続で、$(a,b)$で微分可能とします。

まずは、任意の$c\in(a,b)$に対して$f^\prime(c)=0$ならば$f$は定数関数であることを示します。
これは背理法により示します。

仮に、$f$が定数関数でないとします。
すなわち、$\alpha<\beta$を満たすある$\alpha,\beta\in(a,b)$が存在して、$f(\alpha)\neq f(\beta)$とします。
今、$f:[a,b]\to\mathbb{R}$が連続で、$(a,b)$で微分可能ですので、平均値の定理により
$$(\exists c_0\in(\alpha,\beta))\ {\rm s.t.}\ \frac{f(\beta)-f(\alpha)}{\beta-\alpha}=f^\prime(c_0)$$
です。
さらに、任意の$c\in(a,b)$に対して$f^\prime(c)=0$ですので$f^\prime(c_0)=0$です。
従って、
$$\frac{f(\beta)-f(\alpha)}{\beta-\alpha}=0$$
です。
ここで、$f(\alpha)\neq f(\beta)$でしたので、$f(\alpha)\neq f(\beta)$と$f(\alpha)=f(\beta)$が同時に成り立ったため、矛盾です。

次に、定数関数の微分係数は$0$であることを示します。
$f:[a,b]\to\mathbb{R}$を任意の$x\in[a,b]$に対して$f(x)=c\in\mathbb{R}$(定数)で定めます。
このとき、任意の$t\in(a,b)$に対して、
$$\begin{eqnarray} f^\prime(t)=\lim_{h\to0}\frac{f(t+h)-f(t)}{h}=\lim_{h\to0}\frac{c-c}{h}=0 \end{eqnarray}$$
です。

以上のことから成り立ちます。

定理4.の証明終わり

結

今回は高校数学で証明はせずにイメージで納得していた

• 微分係数が正ならば狭義単調増加関数
• 微分係数が負ならば狭義単調減少関数
• 微分係数が非負(非正)ならば単調増加(減少)関数
• 微分係数が$0$であることと定数関数であることは同値

ということを平均値の定理から証明しました。

イメージしやすい事実ではありますが、「成り立ちそうだな」で終わるのではなく実際本当に正しいのかを証明する必要があります。

次回はテイラーの定理について解説します。

乞うご期待！質問、コメントなどお待ちしております！