- 本記事の内容
- 序
- 関数に対する収束
- で、関数の収束って?
- 実際に証明してみよう!
- 関数の極限の性質とその証明
- 1.\(\displaystyle \lim_{x\to a}(f(x)+g(x))=\lim_{x\to a}f(x)+\lim_{x\to a}g(x)=A+B\)の証明
- 2.\(\displaystyle \lim_{x\to a}(f(x)-g(x))=\lim_{x\to a}f(x)-\lim_{x\to a}g(x)=A-B\)の証明
- 3.\(\displaystyle \lim_{x\to a}f(x)g(x)=\left(\lim_{x\to a}f(x)\right)\cdot\left(\lim_{x\to a}g(x)\right)=AB\)の証明
- 4.\(\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\displaystyle\lim_{x\to a}f(x)}{\displaystyle\lim_{x\to a}g(x)}=\frac{A}{B}\)の証明
- 余談その2(筆者の勘所)
- 結
本記事の内容
本記事は関数の極限について解説する記事である。
本記事を読むにあたり、数列の極限を知っているとより理解が進むと思われるので、次の記事も合わせて参照してください。
また、記法については写像の記事を見ていただけると良いと思われますので、次の記事もご参照ください。
序
以前の【解析学の基礎シリーズ】では、実数の連続性について解説した。
またその中で、数列の極限を解説した。
今回は関数に対する極限を考えてみよう、ということである。
つまり、以前の【解析学の基礎シリーズ】では、\(\{a_n\}_{n\in\mathbb{N}}\)に対して\(\displaystyle \lim_{n\to\infty}a_n\)を考えていたのだが、今回は実数の関数\(f:I\to\mathbb{R}\)(ただし、\(I\subset \mathbb{R}\))に対して\(\displaystyle \lim_{x\to a}f(x)\)(\(x\in I\)が\(a\in \bar{I}\)に近づくときに\(f\)の値がどうなるか)を扱いたい、ということである。
ここで、\(\bar{I}\)は\(\mathbb{R}\)の区間\(I\)の端点を含んだ区間である。
つまり、\(I=(\alpha,\beta),\ (\alpha,\beta],\ [\alpha,\beta),\ [\alpha,\beta]\)の場合、\(\bar{I}=[\alpha,\beta]\)ということである。
ただし、\(I\)は必ずしも有界でなくても良い。
\(I=(\alpha,\infty),\ [\alpha,\infty)\)のときは\(\bar{I}=[\alpha,\infty)\)であり、\(I=(-\infty,\beta),\ (-\infty,\beta]\)のときは\(\bar{I}=(-\infty,\beta]\)である。
\(I=(-\infty,\infty)=\mathbb{R}\)の場合は\(\bar{I}=(-\infty,\infty)=\mathbb{R}\)である。
\(a\in I\)でなく\(a\in\bar{I}\)とする理由は別記事で書きます。
今回の「関数の極限」も数列の極限とは本質的に殆ど変わらない。
数列の場合、すなわち\(\displaystyle \lim_{n\to\infty}a_n=a\)は「項の番号\(n\)が限りなく大きくなっていくとき、ある一定の値に限りなく近づいていくならば、\(\{a_n\}_{n\in\mathbb{N}}\)は\(a\)に収束する。」という意味であった。(※この”限りなく”やら”近づいていく”やらを厳密に記述した主張を\(\epsilon-N\)論法と言ったのだった。)
関数の場合、すなわち\(\displaystyle \lim_{x\to a}f(x)=A\)もほとんど同じである。
これは”おおよそ”「\(x\in I\)が\(a\in\bar{I}\)に限りなく近づいていくならば\(f(x)\)は\(A\in\mathbb{R}\)に収束する。」という意味である。
「なんで関数の極限なんて考えないといけないんですか?」となるかもしれないが、それは現代解析学の基本的な概念である微分法、および積分法が関数の極限を使って表現されているからである。
つまり、微分法と積分法を語る上で、関数の極限を導入しなきゃいけない、ということである。
関数に対する収束
数列の収束との視点の違い
序を読んでいただいた方は「ん?数列の極限とは一味違うんじゃないか?」と思ったかもしれない。
実際そのとおりである。
数列の極限は「番号がどんどん大きくなっていくとき、数列の値はどの値に近づく、または近づかずに発散するのか」という話だった一方で、関数の極限は「\(x\)が定義域とその端点を含んだ区間の中の点に近づいたとき、関数はどの値に近づく、または発散するのか」ということだからである。
つまり、数列の極限は「最終的に値はどうなるの?」ということに興味があるのに対し、関数の極限は「この点で値はどうなるの?」ということに興味がある。
正確ではないかもしれないが、数列の極限は大域的に、関数の極限は局所的に考える、というわけである。
勿論、関数の極限でも大域的に、つまり「最終的に値はどうなるの?」ということも考えるが、どちらかというと局所的に、つまり「この点で値はどうなるの?」ということに興味がある。
なぜなのか、は次回または次次回で説明する。

実関数の収束のイメージ(例と共に)
さて、数列と関数の極限に対する視点の違いが分かったところで、高校数学の復習がてら簡単な極限の例を見てみよう。
例1.
\(I_1=[0,5]\subset\mathbb{R}\)とし、\(f:I_1\to\mathbb{R}\)を\(f(x)=x^2\)で定めたとする。
つまりは、二次関数で定義域を\([0,5]\)に絞った関数である。
このとき、\(x\in I\)が\(3\in I_1\)に近づいたときの\(f\)の値\(f(x)\)はどうなっているかを考えてみよう。
高校数学で数Ⅲ(今はもう違う名前かもしれない)を学んだ方は「そりゃ\(9\)っしょ。」と思うだろう。
正しいです。
これを高校数学の記法で書けば、\(\displaystyle \lim_{x\to3}f(x)=9\)というわけである。

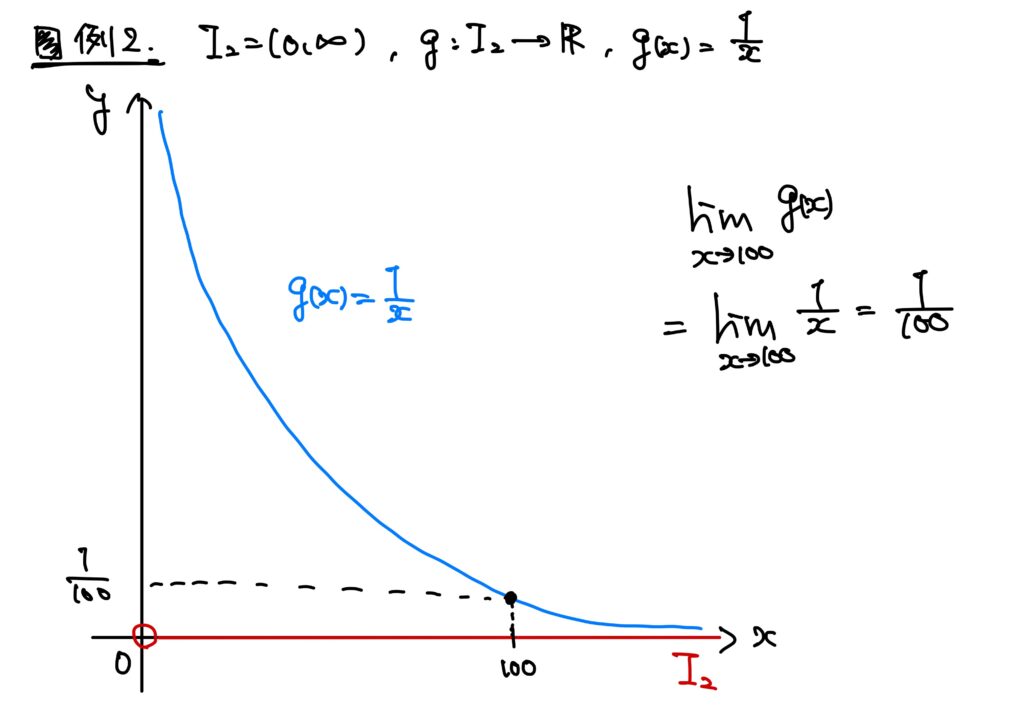
例2.
\(I_2=(0,\infty)=\mathbb{R}_{>0}=\{x\in\mathbb{R}\mid x>0\}\subset\mathbb{R}\)とし、\(g:I_2\to\mathbb{R}\)を\(g(x)=\displaystyle\frac{1}{x}\)で定めたとする。
つまりは、反比例で定義域を正の実数に絞った関数である。
このとき、\(x\in I_2\)が\(100\in I_2\)に近づいたときの\(g\)の値\(g(x)\)はどうなっているかを考えてみよう。
高校数学で数Ⅲを学んだ方は「そりゃ\(\displaystyle\frac{1}{100}\)っしょ。」と思うだろう。
正しいです。
これを高校数学の記法で書けば、\(\displaystyle \lim_{x\to100}g(x)=\frac{1}{100}\)というわけである。
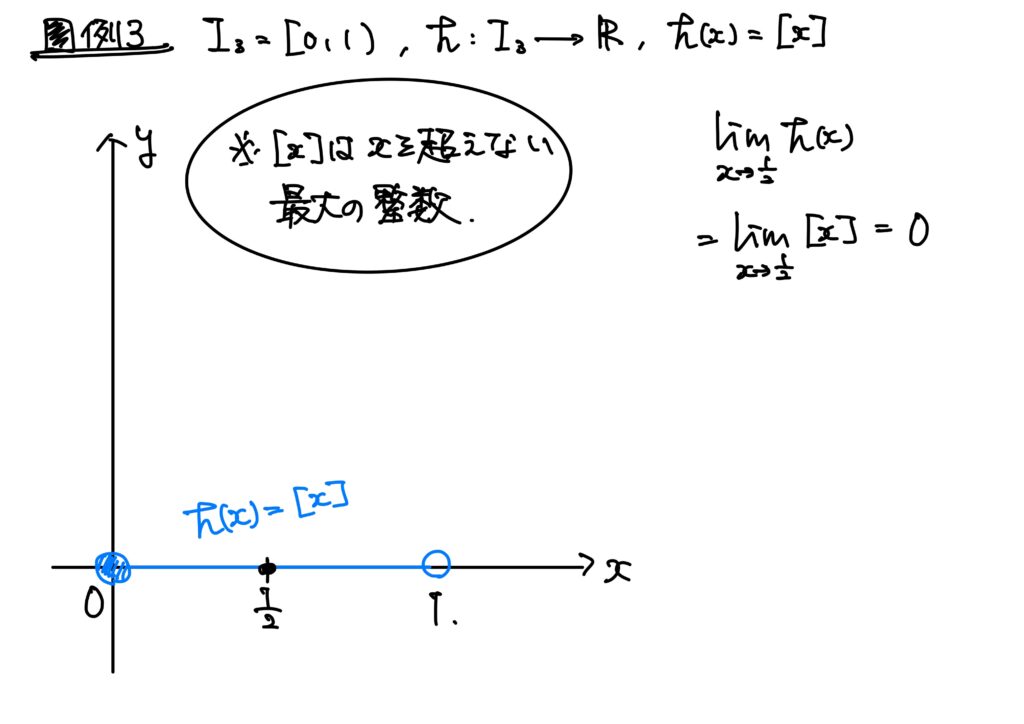
例3.(ガウス記号)
\(I_3=[0,1)\)とし、\(h:I_3\to\mathbb{R}\)を\(h(x)=[x]\)で定めたとする。
ただし、\([x]\)は\(x\)を超えない最大の整数である。
このとき、\(x\in I_3\)が\(\displaystyle\frac{1}{2}\in I_3\)に近づいたときの\(h\)の値\(h(x)\)はどうなっているかを考えてみよう。
答えは\(0\)である。
これを高校数学の記法で書けば、\(\displaystyle \lim_{x\to\frac{1}{2}}h(x)=0\)というわけである。
実関数の収束のイメージ(どう捉えられるか)
数列の収束は「ある番号以降はある値と十分近い」ということが収束のイメージだった。
しかし、実関数は序でも述べたとおり局所的な考え方をするので、まったくもって同じイメージというわけではない。
これにより「おや?分からねえぞ?」となるのではないか。
とはいえ、似ている部分も大いにある。
それについて説明する。
まず、関数の収束の直感的なイメージを1行で述べれば、結局の所
ということである。
少々記号を用いて書けば、関数\(f:I\to\mathbb{R}\)に対して、
ということである。
数列のときを思い出してみると、先の主張の後半の「\(f(x)\)が\(A\)に十分近づく。」は、「任意の正の実数\(\epsilon\)に対して、\(|f(x)-A|<\epsilon\)が成り立つことなんだな。」、つまり
$$(\forall \epsilon>0)\ |f(x)-A|<\epsilon$$
が成り立つことなんだな、と分かっていただけると思う。
では、前半の「\(x\in I\)が\(a\in\bar{I}\)に近づいたとき」について説明する。
これを論理的に捉えるために数列の話を思い出す。
数列は「ある番号以降の数列の値がとある値と十分近いときに収束するという。」のだった。
関数の収束については「\(a\in\bar{I}\)が含まれるとある区間内に入っている\(x\in I\)については、」と言い換えるのである。
「は?」と思うかもしれないので、前後半まとめて書くとわかりやすくなると思われる。
とどのつまり、関数の収束というのは、「\(x\in I\)と\(a\in\bar{I}\)の距離がある値(すなわち、距離)以内であれば、\(f(x)\)と\(A\)の距離\(|f(x)-A|\)が十分小さい。」ということである。
すなわち、
ということである。
数列は「ある番号以降は十分近い。」だったのに対し、関数は「とある範囲内であれば、十分近い。」ということが違いである。
従って、
というわけである。
で、関数の収束って?
上記のことを論理式で書くと、次である。
もう一度言い直しておくと、
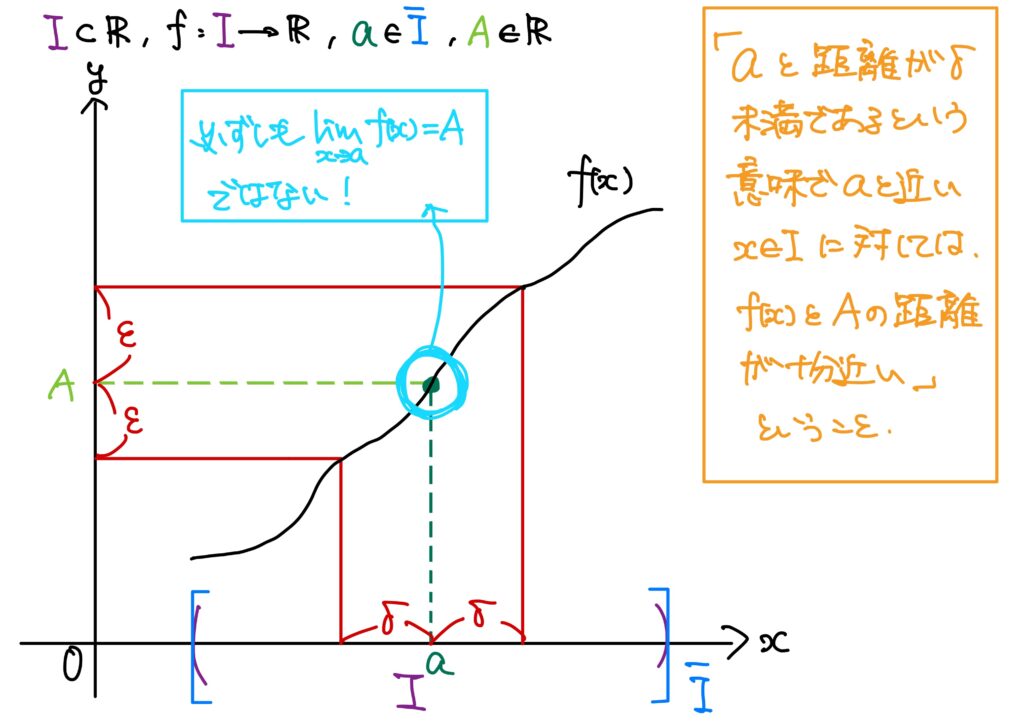
ここで「\(A\)って\(f(a)\)のことじゃねえの?」と思うかもしれないが、必ずしも一致しない。
「本当に?」と思う方は次の単元で例とともに説明するので、それまでお待ち下さい。
実際に証明してみよう!
先に挙げた例1.,2.,3.を厳密に証明してみよう!
余談とし筆者の勘所も述べるつもりなので、もしよかったらそれも読んでいただければ嬉しい。
(証明)
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-3|<\delta\Rightarrow |x^2-9|<\epsilon)$$
である。
すなわち、上記を満たすような\(\delta>0\)を見つけてくればよいわけである。
任意の\(\epsilon>0\)に対して、\(\delta=-3+\sqrt{9+\epsilon}\)とする。(「はぁ?なんだこれ?」と思うかもしれないが、そのときは余談を参照してください。)
すると、\(\epsilon>0\)であるため、\(\delta>0\)である。
\(|x-3|<\delta\)なる\(x\in I\)に対して、
\begin{eqnarray} |x^2-9|&=&|(x+3)(x-3)| \\
&=&|x+3|\cdot |x-3| \\
&=&|x-3+6|\cdot|x-3| \\
&<&\left(|x-3|+|6|\right)\cdot|x-3| \\
&=&|x-3|^2+6|x-3| \\
&<&\delta^2+6\delta \\
&=&(-3+\sqrt{9+\epsilon})^2+6\cdot(-3+\sqrt{9+\epsilon}) \\
&=&9-6\sqrt{9+\epsilon}+9+\epsilon-18+6\sqrt{9+\epsilon}\\
&=&\epsilon
\end{eqnarray}
従って、\(|x^2-9|<\epsilon\)が任意の\(\epsilon>0\)で成り立った。
故に、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-3|<\delta\Rightarrow |x^2-9|<\epsilon)$$
が成り立ったので、\(\displaystyle \lim_{x\to 3}x^2=9\)である。
(Q.E.D.)
この証明を読んで、「お?\(\delta\)の決め方がわかったきがするぞ?」という方はぜひ例2.の証明に挑戦してみてほしい。
(証明)
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-100|<\delta\Rightarrow \left|\frac{1}{x}-\frac{1}{100}\right|<\epsilon\right)$$
である。
すなわち、上記を満たすような\(\delta>0\)を見つけてくればよいわけである。
任意の\(\epsilon>0\)に対して、\(\delta=\epsilon\)とする。
すると、\(\epsilon>0\)であるため、\(\delta>0\)である。
\(|x-100|<\delta\)なる\(x\in I\)に対して、
\begin{eqnarray}
\left|\frac{1}{x}-\frac{1}{100}\right|&=&\left|\frac{100-x}{100x}\right| \\
&<&|100-x|<\delta=\epsilon
\end{eqnarray}
従って、\(\left|\dfrac{1}{x}-\dfrac{1}{100}\right|<\epsilon\)が任意の\(\epsilon>0\)で成り立った。
故に、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-100|<\delta\Rightarrow \left|\frac{1}{x}-\frac{1}{100}\right|<\epsilon\right)$$
が成り立ったので、\(\displaystyle \lim_{x\to 100}\frac{1}{x}=\frac{1}{100}\)である。
(Q.E.D.)
「ふむ。今回は\(\delta\)が\(\epsilon\)なのか。」となっていると嬉しい。
(証明)
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<\left|x-\frac{1}{2}\right|<\delta\Rightarrow |[x]-0|<\epsilon\right)$$
である。
すなわち、上記を満たすような\(\delta>0\)を見つけてくればよいわけである。
任意の\(\epsilon>0\)に対して、\(\delta=\epsilon\)とする。
すると、\(\epsilon>0\)であるため、\(\delta>0\)である。
ここで、任意の\(x\in I\)に対して、\([x]=0\)であることに注意する。
\(\left|x-\dfrac{1}{2}\right|<\delta\)なる\(x\in I\)に対して、
\begin{eqnarray}
|[x]-0|=|0-0|=0<\delta=\epsilon
\end{eqnarray}
従って、\(|[x]-\dfrac{1}{100}|<\epsilon\)が任意の\(\epsilon>0\)で成り立った。
故に、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-\frac{1}{2}|<\delta\Rightarrow \left|[x]-0\right|<\epsilon\right)$$
が成り立ったので、\(\displaystyle \lim_{x\to \frac{1}{2}}[x]=0\)である。
(Q.E.D.)
余談その1(筆者の勘所)
「どうやって\(\delta\)を見つけんだよ!」という話である。
これは実は数列のときの勘所ほとんど同じである。
例1.を解いたときの筆者の頭の中を書く。
〜〜〜筆者の頭の中〜〜〜
\(|x-3|<\delta\)を満たすような\(x\)で\(|x^2-9|<\epsilon\)が成り立つような\(\delta\)を見つけたいんだよね。
もし仮にそんな\(\delta\)があったらば、使える不等式は\(0<|x-3|<\delta\)だけだよな。
じゃあ\(|x^2-9|\)をなんとか\(\delta\)が使える形、\(|x-3|\)が出現する形に直してみるか。 \begin{eqnarray}
|x^2-9|&=&|(x+3)(x-3)| \\
&=&|x+3|\cdot |x-3| \\
&=&|x-3+6|\cdot|x-3| \\
&<&\left(|x-3|+|6|\right)\cdot|x-3| \\
&=&|x-3|^2+6|x-3| \\
&<&\delta^2+6\delta
\end{eqnarray}
なのだから、\(\delta^2+6\delta <\epsilon\)という\(\delta\)が見つけられれば嬉しい。
というより、これを満たす\(\delta\)があればいい!
ということは\(\delta^2+6\delta-\epsilon=0\)という\(\delta\)に対する2次方程式を解きゃいいんじゃんね。
解いてみると…\(\delta=-3\pm\sqrt{9+\epsilon}\)だな。
でも、\(\delta>0\)じゃなきゃいけない。
\(\epsilon>0\)だから、\(\delta=-3-\sqrt{9+\epsilon}<0\)でだめ。 \(\delta=-3+\sqrt{9+\epsilon}>0\)だ。OK。
〜〜〜筆者の頭の中おしまい〜〜〜
要は無理やりゴールから逆算している、ということである。
数列のときにも述べたが、
ということである。
関数の極限の性質とその証明
数列のときと同様に、関数の和、差、積、商の極限にも似た性質がある。
関数の極限の証明の良い練習問題となると思うので是非挑戦してみてほしい。
ただ、初見では「思いつかねえよ!」というのもある(積、商の極限が初見殺し)。
\(I\)を\(\mathbb{R}\)の区間、\(f:I\to\mathbb{R}\)および\(g:I\to\mathbb{R}\)を関数、\(a\in\bar{I}\)、\(A,b\in\mathbb{R}\)とし、\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)とする。 このとき、次が成り立つ。
- \(\displaystyle \lim_{x\to a}(f(x)+g(x))=\lim_{x\to a}f(x)+\lim_{x\to a}g(x)=A+B\),
- \(\displaystyle \lim_{x\to a}(f(x)-g(x))=\lim_{x\to a}f(x)-\lim_{x\to a}g(x)=A-B\),
- \(\displaystyle \lim_{x\to a}f(x)g(x)=\left(\lim_{x\to a}f(x)\right)\cdot\left(\lim_{x\to a}g(x)\right)=AB\),
- \(B\neq0\)ならば、\(\delta_0>0\)が存在して、\(|x-a|<\delta_0\)なる\(x\in I\)に対して、\(g(x)\neq 0\)で、\(\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\displaystyle\lim_{x\to a}f(x)}{\displaystyle\lim_{x\to a}g(x)}=\frac{A}{B}\)
1.\(\displaystyle \lim_{x\to a}(f(x)+g(x))=\lim_{x\to a}f(x)+\lim_{x\to a}g(x)=A+B\)の証明
(1.の証明)
\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)とする。
このとき、示したいことは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |(f(x)+g(x))-(A+B)|<\epsilon)$$
である。 つまり、上記を満たすような\(\delta>0\)を見つけてくれば良い。
今、\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)なのだから、
- \(\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_1\Rightarrow |f(x)-A|<\epsilon_1)\),
- \(\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\epsilon_2)\)
が同時に成り立っている。
すなわち、上記を満たすような、\(\delta_1\)および\(\delta_2\)を見つけることができる。
\(\epsilon_1\)および\(\epsilon_2\)は任意の正の実数なので、\(\epsilon_1\)と\(\epsilon_2\)をまとめて、新たに\(\epsilon>\)を用いて\(\dfrac{\epsilon}{2}\)としても成り立つ。
すると、
- \(\displaystyle\left(\forall \frac{\epsilon}{2}>0\right)(\exists \delta_1>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta_1\Rightarrow |f(x)-A|<\frac{\epsilon}{2}\right)\),
- \(\displaystyle\left(\forall \frac{\epsilon}{2}>0\right)(\exists \delta_2>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\frac{\epsilon}{2}\right)\)
が同時に成り立っている。
\(\delta\)として、先程見つけた\(\delta_1\)と\(\delta_2\)のうち小さい方を採用する(\(\delta=\min\{\delta_1,\delta_2\}\))と、任意の正の実数\(\epsilon\)に対して、\(x\in I\)が\(0<|x-a|<\delta\)ならば\(|f(x)-A|<\dfrac{\epsilon}{2}\)かつ\(|g(x)-B|<\dfrac{\epsilon}{2}\)が成り立っている。
すなわち、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta\Rightarrow |f(x)-A|<\frac{\epsilon}{2}かつ|g(x)-B|<\frac{\epsilon}{2}\right)$$
が成り立っている。
このとき、
\begin{eqnarray}
|(f(x)+g(x))-(A+B)|&=&|(f(x)-A)+(g(x)-B)| \\
&<&|f(x)-A|+|g(x)-B|\\
&<&\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon
\end{eqnarray}
である。
従って、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta\Rightarrow |(f(x)+g(x))-(A+B)|<\epsilon\right)$$
が成り立つので、
$$\lim_{x\to a}(f(x)+g(x))=\lim_{x\to a}f(x)+\lim_{x\to a}g(x)=A+B$$
である。
(Q.E.D.)
2.\(\displaystyle \lim_{x\to a}(f(x)-g(x))=\lim_{x\to a}f(x)-\lim_{x\to a}g(x)=A-B\)の証明
1.と殆ど同じであるので、ぜひ1.をマネして証明に挑戦してみてほしい。
(2.の証明)
\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)とする。
このとき、示したいことは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |(f(x)-g(x))-(A-B)|<\epsilon)$$
である。
つまり、上記を満たすような\(\delta>0\)を見つけてくれば良い。
今、\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)なのだから、
- \(\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_1\Rightarrow |f(x)-A|<\epsilon_1)\),
- \(\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\epsilon_2)\)
が同時に成り立っている。
すなわち、上記を満たすような、\(\delta_1\)および\(\delta_2\)を見つけることができる。
\(\epsilon_1\)および\(\epsilon_2\)は任意の正の実数なので、\(\epsilon_1\)と\(\epsilon_2\)をまとめて、新たに\(\epsilon>\)を用いて\(\dfrac{\epsilon}{2}\)としても成り立つ。
すると、
- \(\displaystyle\left(\forall \frac{\epsilon}{2}>0\right)(\exists \delta_1>0)\ {\rm s.t.}\ \left(\forall x\in I\ |x-a|<\delta_1\Rightarrow |f(x)-A|<\frac{\epsilon}{2}\right)\),
- \(\displaystyle\left(\forall \frac{\epsilon}{2}>0\right)(\exists \delta_2>0)\ {\rm s.t.}\ \left(\forall x\in I\ |x-a|<\delta_2\Rightarrow |g(x)-B|<\frac{\epsilon}{2}\right)\)
が同時に成り立っている。
\(\delta\)として、先程見つけた\(\delta_1\)と\(\delta_2\)のうち小さい方を採用する(\(\delta=\min\{\delta_1,\delta_2\}\))と、任意の正の実数\(\epsilon\)に対して、\(x\in I\)が\(0<|x-a|<\delta\)ならば\(|f(x)-A|<\dfrac{\epsilon}{2}\)かつ\(|g(x)-B|<\dfrac{\epsilon}{2}\)が成り立っている。
すなわち、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ |x-a|<\delta\Rightarrow |(f(x)-A|<\frac{\epsilon}{2}かつ|g(x)-B|<\frac{\epsilon}{2}\right)$$
が成り立っている。
このとき、
\begin{eqnarray}
|(f(x)-g(x))-(A-B)|&=&|(f(x)-A)+(B-g(x))| \\
&<&|f(x)-A|+|B-g(x)|\\
&<&\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon
\end{eqnarray} である。
従って、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ |x-a|<\delta\Rightarrow |(f(x)-g(x))-(A-B)|<\epsilon)$$
が成り立つので、
$$\lim_{x\to a}(f(x)-g(x))=\lim_{x\to a}f(x)-\lim_{x\to a}g(x)=A-B$$
である。
(Q.E.D.)
3.\(\displaystyle \lim_{x\to a}f(x)g(x)=\left(\lim_{x\to a}f(x)\right)\cdot\left(\lim_{x\to a}g(x)\right)=AB\)の証明
1.,2.と比べて少々テクニカルである。
(3.の証明)
\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)とする。
このとき、示したいことは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ |x-a|<\delta\Rightarrow |(f(x)g(x))-AB|<\epsilon)$$
である。
つまり、上記を満たすような\(\delta>0\)を見つけてくれば良い。
今、\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)なのだから、
- \(\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_1\Rightarrow |f(x)-A|<\epsilon_1)\),
- \(\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\epsilon_2)\)
が同時に成り立っている。
すなわち、上記を満たすような、\(\delta_1\)および\(\delta_2\)を見つけることができる。
ここで、
$$\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I\ |x-a|<\delta_1\Rightarrow |f(x)-A|<\epsilon_1)$$
が成り立っているのだから、\(\epsilon_1=1\)としても成り立つ。
故に、\(0<|x-a|<\delta_1\)なる\(x\in I\)に対して、\(|f(x)-A|<1\)が成り立っている。
\(|f(x)|-|A|\leq |f(x)-A|<1\)(\(|a|-|b|\leq|a-b|\)を使っている)なのだから、\(|f(x)|<1+|A|\)である。
すなわち、\(0<|x-a|<\delta_1\)なる\(x\in I\)については、\(f\)は有界なのである。
さて、\(\epsilon_1\)および\(\epsilon_2\)は任意の正の実数なので、\(\epsilon>0\)を用いて\(\epsilon_1=\dfrac{\epsilon}{2|B|}\)、\(\epsilon_2=\dfrac{\epsilon}{2(1+|A|)}\)としても成り立つ。
すると、
- \(\displaystyle\left(\forall \frac{\epsilon}{2|B|}>0\right)(\exists \delta_1>0)\ {\rm s.t.}\ \left(\forall x\in I\ |x-a|<\delta_1\Rightarrow |f(x)-A|<\frac{\epsilon}{2|B|}\right)\),
- \(\displaystyle\left(\forall \frac{\epsilon}{2(1+|A|)}>0\right)(\exists \delta_2>0)\ {\rm s.t.}\ \left(\forall x\in I\ |x-a|<\delta_2\Rightarrow |g(x)-B|<\frac{\epsilon}{2(1+|A|)}\right)\)
が同時に成り立っている。
\(\delta\)として、先程見つけた\(\delta_1\)と\(\delta_2\)のうち小さい方を採用する(\(\delta=\min\{\delta_1,\delta_2\}\))と、任意の正の実数\(\epsilon\)に対して、\(x\in I\)が\(0<|x-a|<\delta\)ならば\(\displaystyle|f(x)-A|<\frac{\epsilon}{2|B|}\)かつ\(\displaystyle|g(x)-B|<\frac{\epsilon}{2(1+|A|)}\)が成り立っている。
すなわち、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ |x-a|<\delta\Rightarrow |(f(x)-A|<\frac{\epsilon}{2|B|}かつ|g(x)-B|<\frac{\epsilon}{2(1+|A|)}\right)$$
が成り立っている。
このとき、
\begin{eqnarray}
|f(x)g(x)-AB|&=&|f(x)g(x)-AB+f(x)B+f(x)B|\\
&=&|f(x)(g(x)-B)+B(f(x)-A)|\\
&\leq&|f(x)|\cdot|g(x)-B|+|B|\cdot|f(x)-A|\\
&<&(1+|A|)\cdot|g(x)-B|+|B|\cdot|f(x)-A|\\
&<&(1+|A|)\cdot \frac{\epsilon}{2(1+|A|)}+|B|\cdot \frac{\epsilon}{2|B|}\\
&=&\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon
\end{eqnarray}
である。
従って、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ |x-a|<\delta\Rightarrow |(f(x)g(x)-AB|<\epsilon)$$
が成り立つので、
$$\displaystyle \lim_{x\to a}f(x)g(x)=\left(\lim_{x\to a}f(x)\right)\cdot\left(\lim_{x\to a}g(x)\right)=AB$$
である。
(Q.E.D.)
4.\(\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\displaystyle\lim_{x\to a}f(x)}{\displaystyle\lim_{x\to a}g(x)}=\frac{A}{B}\)の証明
これは初見殺しである。
とはいえ、3.と似てる。
しかしやはりテクニカルなので、流れを説明する。
- (ステップ1) \(|f(x)|\)と\(|g(x)|\)がある範囲では上に有界であることを示す。
- (ステップ2) \(|g(x)|\)はある範囲で下に有界であることを示す。
- (ステップ3) \(\delta\)を適切にとり、式変形して証明する。
(4.の証明)
\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)とする。
このとき、示したいことは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta\Rightarrow \left|\frac{f(x)}{g(x)}-\frac{A}{B}\right|<\epsilon\right)$$
である。
つまり、上記を満たすような\(\delta>0\)を見つけてくれば良い。
今、\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)なのだから、
- \(\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_1\Rightarrow |f(x)-A|<\epsilon_1),\cdots①\)
- \(\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\epsilon_2)\cdots②\)
が同時に成り立っている。
すなわち、上記を満たすような、\(\delta_1\)および\(\delta_2\)を見つけることができる。
(ステップ1)
ここで、
$$\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_1\Rightarrow |f(x)-A|<\epsilon_1)$$
が成り立っているのだから、\(\epsilon_1=1\)としても成り立つ。
故に、\(0<|x-a|<\delta_1\)なる\(x\in I\)に対して、\(|f(x)-A|<1\)が成り立っている。
\(|f(x)|-|A|\leq |f(x)-A|<1\)(\(|a|-|b|\leq|a-b|\)を使っている)なのだから、\(|f(x)|<1+|A|\)である。 すなわち、\(|x-a|<\delta_1\)なる\(x\in I\)については、\(|f(x)|\)は上に有界なのである。
また、同様に、
$$\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\epsilon_2)$$
が成り立っているのだから、\(\epsilon_1=1\)としても成り立つ。
故に、\(0<|x-a|<\delta_2\)なる\(x\in I\)に対して、\(|g(x)-A|<1\)が成り立っている。
\(|g(x)|-|B|\leq |g(x)-B|<1\)(\(|a|-|b|\leq|a-b|\)を使っている)なのだから、\(|g(x)|<1+|B|\)である。
すなわち、\(|x-a|<\delta_2\)なる\(x\in I\)については、\(|g(x)|\)は上に有界なのである。
(ステップ2)
実は、\(|f(x)|\)と\(|g(x)|\)は下にも有界である。
今回は\(|g(x)|\)が下に有界であることが重要なので、\(|g(x)|\)が下に有界であることを示す。
$$\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\epsilon_2)$$
が成り立っているのだから、\(0<|x-a|<\delta_2\)なる\(x\in I\)に対しては、\(|g(x)-B|<\epsilon_2\)が任意の\(\epsilon_2>\)に対して成り立っている。
従って、\(\epsilon_2=\dfrac{|B|}{2}\)としても成り立つ。
故に、
$$|g(x)|=|g(x)-B+B|\geq |B|-|g(x)-B|>|B|-\frac{|B|}{2}=\frac{|B|}{2}>0$$
が成り立つ。
ただし、\(|a+b|\geq |b|-|a|\)を用いた。
従って、\(|x-a|<\delta_2\)なる\(x\in I\)に対しては、\(|g(x)|>\dfrac{|B|}{2}\)により、下に有界である。
(ステップ3)
さて、\(\epsilon_1\)および\(\epsilon_2\)は任意の正の実数なので、\(\epsilon>0\)を用いて\(\displaystyle\epsilon_1=\frac{|B|\cdot \frac{|B|}{2}}{2(1+|B|)}\epsilon\)、\(\displaystyle\epsilon_2=\frac{|B|\cdot \frac{|B|}{2}}{2(1+|A|)}\epsilon\)としても成り立つ。
すると、
- \(\displaystyle(\forall \frac{|B|\cdot \frac{|B|}{2}}{2(1+|B|)}\epsilon>0)(\exists \delta_1>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta_1\Rightarrow |f(x)-A|<\frac{|B|\cdot \frac{|B|}{2}}{2(1+|B|)}\epsilon\right)\),
- \(\displaystyle(\forall \frac{|B|\cdot \frac{|B|}{2}}{2(1+|A|)}\epsilon>0)(\exists \delta_2>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\frac{|B|\cdot \frac{|B|}{2}}{2(1+|A|)}\epsilon\right)\)
が同時に成り立っている。
\(\delta\)として、先程見つけた\(\delta_1\)と\(\delta_2\)のうち小さい方を採用する(\(\delta=\min\{\delta_1,\delta_2\}\))と、任意の正の実数\(\epsilon\)に対して、\(x\in I\)が\(0<|x-a|<\delta\)ならば\(\displaystyle|f(x)-A|<\frac{|B|\cdot \frac{|B|}{2}}{2(1+|B|)}\epsilon\)かつ\(\displaystyle|g(x)-B|<\frac{|B|\cdot \frac{|B|}{2}}{2(1+|A|)}\epsilon\)が成り立っている。
すなわち、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta\Rightarrow\\|(f(x)-A|<\frac{|B|\cdot \frac{|B|}{2}}{2(1+|B|)}\epsilonかつ|g(x)-B|<\frac{|B|\cdot \frac{|B|}{2}}{2(1+|A|)}\epsilon\right)$$
が成り立っている。
このとき、
\begin{eqnarray}
\left|\frac{f(x)}{g(x)}-\frac{A}{B}\right|&=&\left|\frac{B\cdot f(x)-A\cdot g(x)}{B\cdot g(x)} \right|\\
&=&\left|\frac{B\cdot f(x)-A\cdot g(x)+f(x)g(x)-f(x)g(x)}{B\cdot g(x)} \right|\\
&=&\left|\frac{f(x)\cdot(B-g(x))+g(x)\cdot (f(x)-A)}{B\cdot g(x)} \right|\\
&=&\frac{|f(x)|\cdot|B-g(x)|+|g(x)|\cdot|f(x)-A|}{|B|\cdot|g(x)|}\\
&<&\frac{1}{|B|\cdot\frac{|B|}{2}}\left((1+|A|)\cdot \frac{|B|\cdot \frac{|B|}{2}}{2(1+|A|)}\epsilon +(1+|B|)\cdot \frac{|B|\cdot \frac{|B|}{2}}{2(1+|B|)}\epsilon\right)\\
&=&\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon
\end{eqnarray}
である。
従って、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-a|<\delta\Rightarrow \left|\frac{f(x)}{g(x)}-\frac{A}{B}\right|<\epsilon\right)$$
が成り立つので、
\(g(x)\neq 0\)で、\(\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\displaystyle\lim_{x\to a}f(x)}{\displaystyle\lim_{x\to a}g(x)}=\frac{A}{B}\)
である。
(Q.E.D.)
余談その2(筆者の勘所)
余談その1で述べた勘所とは少々違った勘所が必要なのが、上記の和・差・積・商の証明である。
そもそも関数の収束は
のであった。
要は、そういう距離\(\delta\)を見つけてきなさい。ということであった。
1.を証明するときを思い出してみる。
\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)なのだから、
- \(\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_1\Rightarrow |f(x)-A|<\epsilon_1)\),
- \(\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta_2\Rightarrow |g(x)-B|<\epsilon_2)\)
が成り立っている。
故に、\(\delta_1\)と\(\delta_2\)のうち、小さい方を採用して新たに\(\delta\)と、書くことにすると、\(0<|x-a|<\delta\)なる\(x\in I\)で、\(|f(x)-A|<\epsilon_1\)と\(|g(x)-B|<\epsilon_2\)が同時に成り立つ。
これで見つけたい距離\(\delta\)の候補を見つけることができた。
そんな\(\delta\)で\(|(f(x)+g(x))-(A+B)|<\epsilon\)が成り立ってほしいわけである。
これを変形していくと
\begin{eqnarray}
|(f(x)+g(x))-(A+B)|&=&|(f(x)-A)+(g(x)-B)| \\
&<&|f(x)-A|+|g(x)-B|\\
&<&\epsilon_1+\epsilon_2
\end{eqnarray}
となる。
ここで、\(\epsilon_1\)も\(\epsilon_2\)も任意の正の実数なのだから、正の実数であれば何でも良いわけである。
新たに\(\epsilon\)という記号を用意して、\(\epsilon\)が任意の正の実数だとしたら\(\epsilon_1\)と\(\epsilon_2\)は任意の正の実数なのだから、\(\epsilon_1=\dfrac{\epsilon}{2}\)、\(\epsilon_2=\dfrac{\epsilon}{2}\)としたって成り立つわけである。
これでようやっと
\begin{eqnarray}
|(f(x)+g(x))-(A+B)|&=&|(f(x)-A)+(g(x)-B)| \\
&<&|f(x)-A|+|g(x)-B|\\
&<&\epsilon_1+\epsilon_2\\
&=&\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon
\end{eqnarray}
を得られることが分かった。
その後に文字に起こして、1.のような証明の流れにするわけである。
「なんでこんなことしなきゃいけないの?」と思うかもしれない。
実のところ、こんなこと(帳尻合わせ)をしなくても良い。
しかしながら、帳尻をあわせた方が見栄えが良いのである。
つまり、帳尻は合わせなくても間違いでないし議論に差し支えない。
しかし、誰が見てもパット見て「正しい」と判断できるためには帳尻をあわせたほうがよい。
4.の証明も同様である。
まずは、式を変形してみる。
\begin{eqnarray}
\left|\frac{f(x)}{g(x)}-\frac{A}{B}\right|&=&\left|\frac{B\cdot f(x)-A\cdot g(x)}{B\cdot g(x)} \right|\\
&=&\left|\frac{B\cdot f(x)-A\cdot g(x)+f(x)g(x)-f(x)g(x)}{B\cdot g(x)} \right|\\
&=&\left|\frac{f(x)\cdot(B-g(x))+g(x)\cdot (f(x)-A)}{B\cdot g(x)} \right|\\
&=&\frac{|f(x)|\cdot|B-g(x)|+|g(x)|\cdot|f(x)-A|}{|B|\cdot|g(x)|}\\
\end{eqnarray}
となる。
つまり、
$$\frac{|f(x)|\cdot|B-g(x)|+|g(x)|\cdot|f(x)-A|}{|B|\cdot|g(x)|}<\epsilon$$
としたいわけである。
ここまで来てから、「\(|f(x)|\)が上に有界で、\(|g(x)|\)が上にも下にも有界だったらいいなあ」と思うわけである。
もしこれが正しければ、つまり、\(|f(x)|<M_f\)、\(0<L_g<|g(x)|<M_g\)という実数\(M_f,\ L_g,\ M_g\)があれば、
\begin{eqnarray}
&&\frac{|f(x)|\cdot|B-g(x)|+|g(x)|\cdot|f(x)-A|}{|B|\cdot|g(x)|}\\
&<&\frac{M_f\cdot|B-g(x)|+M_g\cdot|f(x)-A|}{|B|\cdot L_g}\\
\end{eqnarray}
となり、\(|f(x)-A|<\epsilon_1\)かつ\(|g(x)-B|<\epsilon_2\)なのだから、
\begin{eqnarray}
&&\frac{|f(x)|\cdot|B-g(x)|+|g(x)|\cdot|f(x)-A|}{|B|\cdot|g(x)|}\\
&<&\frac{M_f\cdot|B-g(x)|+M_g\cdot|f(x)-A|}{|B|\cdot L_g}\\
&<&\frac{M_f\cdot\epsilon_2+M_g\cdot\epsilon_1}{|B|\cdot L_g}
\end{eqnarray}
となって、後は\(\epsilon_1\)と\(\epsilon_2\)の帳尻合わせをすれば終わるからである。
これにより、\(|f(x)|\)と\(|g(x)|\)が有界かどうかを考えるのである。
(※\(M_f,\ L_g,\ M_g\)はそれぞれ、4.の証明において、\(\displaystyle M_f=1+|A|\)、\(L_g=\dfrac{|B|}{2}\)、\(M_g=1+|B|\)に対応する。)
その後、これらが有界である事がわかったので、
\begin{eqnarray}
\left|\frac{f(x)}{g(x)}-\frac{A}{B}\right|<\frac{M_f\cdot\epsilon_2+M_g\cdot\epsilon_1}{|B|\cdot L_g}
\end{eqnarray}
が正しい、ということが分かった。
その後にようやっと、
$$\frac{M_f\cdot\epsilon_2+M_g\cdot\epsilon_1}{|B|\cdot L_g}<\epsilon$$
にするための\(\epsilon_1\)と\(\epsilon_2\)の帳尻合わせを行うのである。
帳尻合わせのやり方は人それぞれだと思うのだが、筆者の場合について書く。
まずは\(\epsilon_2\)について考えてみよう。
\(\displaystyle\frac{M_f\cdot\epsilon_2+M_g\cdot\epsilon_1}{|B|\cdot L_g}\)を全部まとめて\(\epsilon\)と表記したいのだから、\(M_f\)が邪魔である。
故に、とりあえず、\(\epsilon_2=\dfrac{1}{M_f}\epsilon\)としてみる。
これだ分母が余って約分できない。
よって、次に\(\epsilon_2=\dfrac{|B|\cdot L_g}{M_f}\epsilon\)としてみる。
同じようにして、\(\epsilon_1=\dfrac{|B|\cdot L_g}{M_g}\epsilon\)としてみる。
すると、
$$\frac{M_f\cdot\epsilon_2+M_g\cdot\epsilon_1}{|B|\cdot L_g}=\frac{M_f\cdot\dfrac{|B|\cdot L_g}{M_f}\epsilon+M_g\cdot\dfrac{|B|\cdot L_g}{M_g}\epsilon}{|B|\cdot L_g}=2\epsilon$$
となる。
「ありゃ。\(2\epsilon\)になっちゃった。」というわけで、\(\epsilon_1\)と\(\epsilon_2\)を\(2\)で割る。
従って、\(\epsilon_1=\dfrac{|B|\cdot L_g}{2M_g}\epsilon\)、\(\epsilon_2=\dfrac{|B|\cdot L_g}{M_f}\epsilon\)を導き出すのである。
これらにより、
$$\left|\frac{f(x)}{g(x)}-\frac{A}{B}\right|<\frac{M_f\cdot\dfrac{|B|\cdot L_g}{2M_f}\epsilon+M_g\cdot\dfrac{|B|\cdot L_g}{2M_g}\epsilon}{|B|\cdot L_g}=\epsilon$$
を得るわけである。
結
今回は関数の極限について記した。
関数の極限は一言で言えば、
砕けた言い方をすれば、「定義域内のある範囲に入っている要素については、その要素に対応する関数の値がある値と十分近いときに収束するという。」ということである。
次回は「関数の連続」について説明する。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!





コメントをする