本記事の内容
本記事は関数の連続性について解説する記事である。
本記事を読むにあたり、関数の極限を知っている必要があるため、その際は以下の記事を参照してください。
序
以前の記事(関数の極限を理解する その1)で述べたとおり、関数の極限と数列の極限との違いは、
- 数列の極限:最終的に値がどうなるの?
- 関数の極限:この点で値はどうなるの?
であった。
一言で言えば、数列の極限は大域的に、関数の極限は局所的に考える、ということである。
なぜ関数の極限は局所的に考えるのか、というと、関数に対しては今回解説する「連続性」という性質を知りたいからである。
関数の連続性は以前の実数の連続性とはまた別の話であるものの、考え方は非常に似ている。
要は、関数がある点でつながっている、ということなのである。
関数が連続であると、嬉しいことがたくさんある。
例えば、閉区間\([a,b]\)において関数\(f\)が連続であれば、\([a,b]\)において\(f\)は最大値および最小値を持つ。
つまり、閉区間内で連続であれば、最大値と最小値の存在が保証される、というわけである。
関数の連続のイメージ
序で述べたことが全てといえば全てであるが、例を挙げよう。
例1.
\(f:\mathbb{R}\to\mathbb{R}\)が\(f(x)=2x\)とする。
このとき、\(f\)は\(\mathbb{R}\)でつながっており、特に\(x=0\)でつながっている。

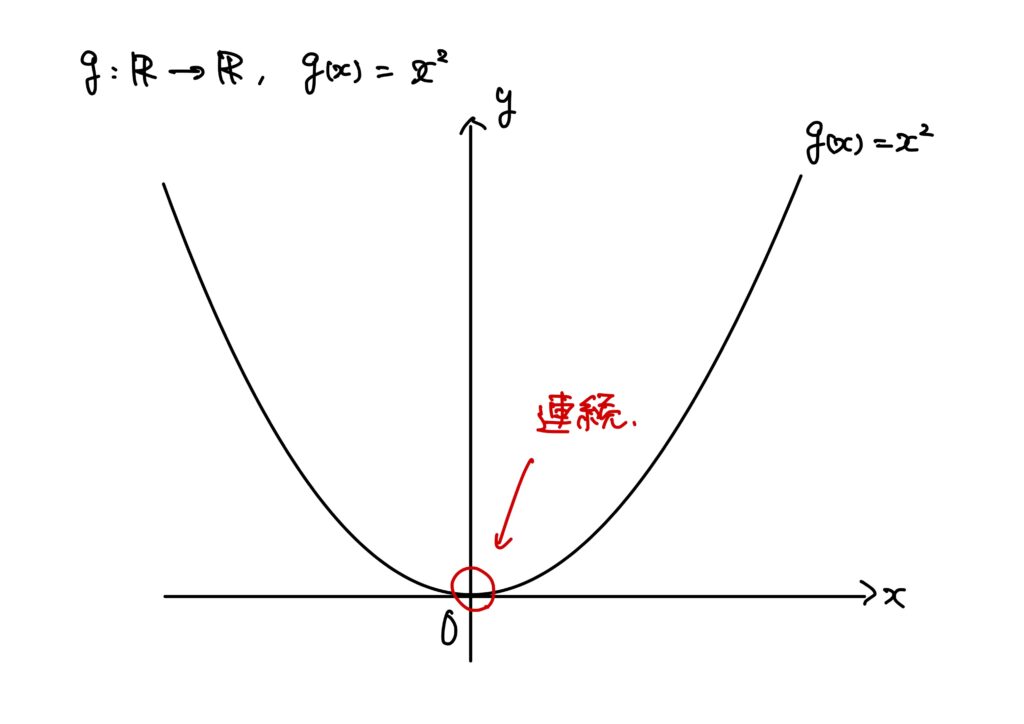
例2.
\(g:\mathbb{R}\to\mathbb{R}\)が\(g(x)=x^2\)で定められているとする。
このとき、\(g\)は\(\mathbb{R}\)でつながっており、特に\(x=0\)でつながっている。

例3.
\(h:\mathbb{R}\to\mathbb{R}\)が\(h(x)=[x]\)([]はGauss記号)とする。
このとき\(h\)は\(x\in\mathbb{Z}\)でつながっていない。
ここで、\([x]\)は\(x\)を超えない最大の整数である。
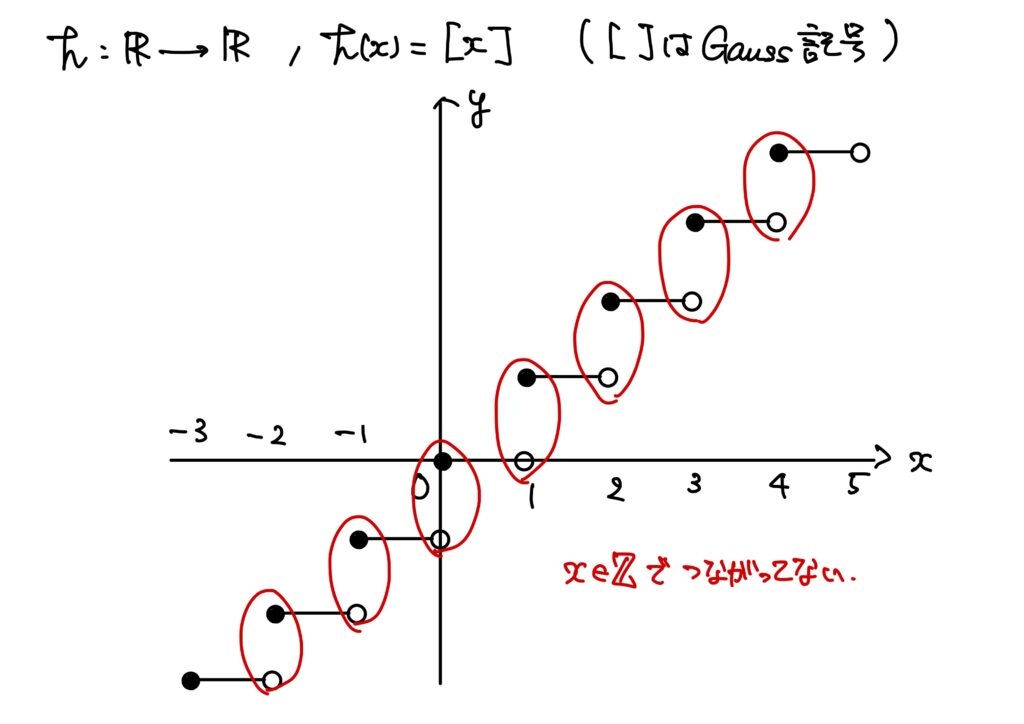
要は
というわけである。
“つながっている”ってどういうこと?
「”つながっている”というのは直感的に分かるけど、それを数学的に表すとどういうこと?」となるだろう。
これは極限を用いて表す事ができるのである。
ここで、発想を実数の連続性へと戻してみよう。
実数の連続性には2つの直感がある、という話をした(「実数の連続性のイメージをつかもう!」【解析学の基礎シリーズ】)。
それは
- 実数の数直線上には一切”すき間”が無い。
- どんな実数にもその十分近くにまた実数がある。
だった。
まず1.を思い浮かべてみよう。
関数の連続に話を戻すと、”つながっている”ということは”途切れていない”ということなのだから、”一切すき間が無い”ということなのである。
実数の連続性では数直線にすき間が無い、という発想だったのだが、関数の連続は”関数のグラフにすき間が無い”ということなのである。
つまり、イメージとしては数直線をグネグネに曲げたりした線(関数のグラフ)にすき間がない、ということである。
次に2.を思い浮かべてみよう。
実数の連続性については「数直線上のどんな実数に対しても、その十分近くにまた実数がある」ということだった。
この数直線をグネグネ曲げて関数の形にしたと想像してほしい。
このとき、「関数のグラフ上のどんな値に対しても、その十分近くにまた関数の値がある」ということが関数の連続なのである。
これをより数学の言葉に近い形で言えば、
わけなのである。
故に関数の連続は極限の言葉を用いて書かれるのである。
実関数の収束は何だったか、というと、
だった。
\(a\in\bar{I}\)と距離が\(\delta\)未満であるような\(x\in I\)に対して、\(f(x)\)と\(A\in\mathbb{R}\)が十分近いときに\(f\)は\(A\)に収束する、ということだった。
この\(A\)が\(f(a)\)と一致しているときに「連続である」というわけなのである。
「あれ?なんかおかしいぞ?」と思うかもしれない。
「\(A\)って\(f(a)\)のことじゃないの?」という疑問が湧くのではなかろうか。
実は違う。
例えばこんな例を考えてみる。
例4.
\(u:\mathbb{R}\to\mathbb{R}\)が
$$u(x)=\begin{cases}
x+2&(x\in\mathbb{R}\setminus \{1\})\\
1&(x=1)
\end{cases}$$
で定められていたとする。
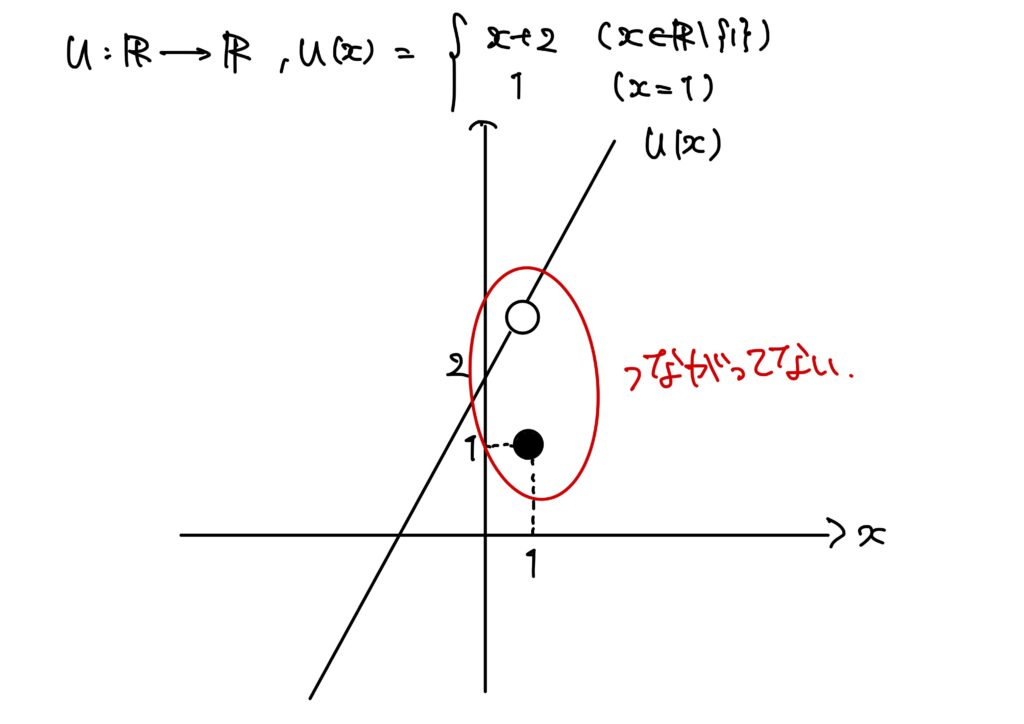
このとき、\(\displaystyle \lim_{x\to 1}u(x)=3\)である。
しかし、\(u(1)=1\)であるので、\(u(1)\neq3\)である。
すなわち、必ずしも\(\displaystyle \lim_{x\to a}u(x)\)と\(u(a)\)は一致しないのである。
ちなみに、この場合は\(u\)は\(x=1\)で連続でない(不連続であるともいう)。
で?関数の連続って数学的にどういうこと?
以上のことをまとめると、関数における連続とはつぎのことをいう。
- \(a\in I\)とする。\(f\)が\(a\)で連続(continuous at \(a\))であるとは、 $$\lim_{x\to a}f(x)=f(a)$$ が成り立つことをいう。 すなわち、 $$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I;\ 0<|x-a|<\delta\Rightarrow |f(x)-f(a)|<\epsilon)$$ が成り立つことをいう。
- \(f\)が\(I\)で連続である(continuous on \(I\))とは、任意の\(a\in I\)に対して、\(f\)が\(a\)で連続であることをいう。 すなわち、 $$(\forall a\in I)(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |f(x)-f(a)|<\epsilon)$$ が成り立つことをいう。

実は、関数の連続には別の言い方もある。
それについては後述する。
関数が連続であることと連続でないことを証明してみよう!
先に挙げた例1.,2.,3.,4.が連続であるかどうかを証明してみよう!
とはいえ、関数の極限、特に関数の収束がわかっていればなんてことはない。
むしろほとんど同じである。
なぜならば、形式的には関数の収束における\(A\)が\(f(a)\)に変わっただけだからである。
「ちょっとやってみようかな。」という方は是非挑戦してみてほしい!
例1.について
例1.
\(f:\mathbb{R}\to\mathbb{R}\)が\(f(x)=2x\)とする。
このとき、\(f\)は\(\mathbb{R}\)で連続であり、特に\(x=0\)で連続である。

証明
- \(f\)が\(x=0\)で連続であることの証明
示したいことは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-0|<\delta\Rightarrow |2x-0|<\epsilon)$$
である。 つまり、任意の\(\epsilon>0\)に対して上記を満たすような\(\delta>0\)を見つけてきなさい、ということである。
\(\displaystyle\delta=\frac{\epsilon}{2}\)とすると、\(\delta>0\)である。
\(0<|x-0|=|x|<\delta\)を満たす\(x\in\mathbb{R}\)に対して、
$$|2x-0|=|2x|=2|x|<2\delta=2\cdot\frac{\epsilon}{2}=\epsilon$$
が成り立つ。
従って、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0|x|<\delta\Rightarrow |2x|<\epsilon)$$
が成り立ったので、\(f\)は\(x=0\)で連続である。 - \(f\)が\(\mathbb{R}\)で連続であることの証明
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
である。
つまり、任意の\(\epsilon>0\)に対して上記を満たすような\(\delta>0\)を見つけてきなさい、ということである。
\(\delta=\frac{\epsilon}{2}\)とすると、\(\delta>0\)である。
\(0<|x-a|<\delta\)を満たす\(x\in\mathbb{R}\)に対して、
$$|2x-2a|=2|x-a|<2\delta=2\cdot\frac{\epsilon}{2}=\epsilon$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
が成り立ったので、\(f\)は\(\mathbb{R}\)で連続である。(Q.E.D.)
例2.について(例1.の証明をマネしてやってみよう!)
例2.
\(g:\mathbb{R}\to\mathbb{R}\)が\(g(x)=x^2\)で定められているとする。
このとき、\(g\)は\(\mathbb{R}\)で連続であり、特に\(x=0\)で連続である。
証明
- \(g\)が\(x=0\)で連続であることの証明
示したいことは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-0|<\delta\Rightarrow |x^2-0|<\epsilon)$$
である。
つまり、任意の\(\epsilon>0\)に対して上記を満たすような\(\delta>0\)を見つけてきなさい、ということである。
\(\delta=\sqrt{\epsilon}\)とすると、\(\delta>0\)である。
\(0<|x-0|=|x|<\delta\)を満たす\(x\in\mathbb{R}\)に対して、
$$|x^2-0|=|x^2|=x^2<\delta^2<\epsilon$$が成り立つ。
従って、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x|<\delta\Rightarrow |x^2|<\epsilon)$$
が成り立ったので、\(f\)は\(x=0\)で連続である。 - \(f\)が\(\mathbb{R}\)で連続であることの証明
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
である。
つまり、任意の\(\epsilon>0\)に対して上記を満たすような\(\delta>0\)を見つけてきなさい、ということである。
\(\delta=-|a|+\sqrt{|a|^2+\epsilon}\)とすると、\(\delta>0\)である。
\(0<|x-a|<\delta\)を満たす\(x\in\mathbb{R}\)に対して、
\begin{eqnarray}
|x^2-a^2|&=&|(x+a)(x-a)|\\
&=&|x-a+2a|\cdot|x-a|\leq |x-a|^2+2|a|\cdot|x-a|\\
&=&|a|^2-2|a|\sqrt{|a|^2+\epsilon}+|a^2|+\epsilon+2|a|(-|a|+\sqrt{|a|^2+\epsilon})\\
&=&2|a|^2-2|a|^2+2|a|\sqrt{|a|^2+\epsilon}-2|a|\sqrt{|a|^2+\epsilon}+\epsilon=\epsilon \end{eqnarray}
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |x^2-a^2|<\epsilon)$$
が成り立ったので、\(f\)は\(\mathbb{R}\)で連続である。
(Q.E.D.)
例3.について
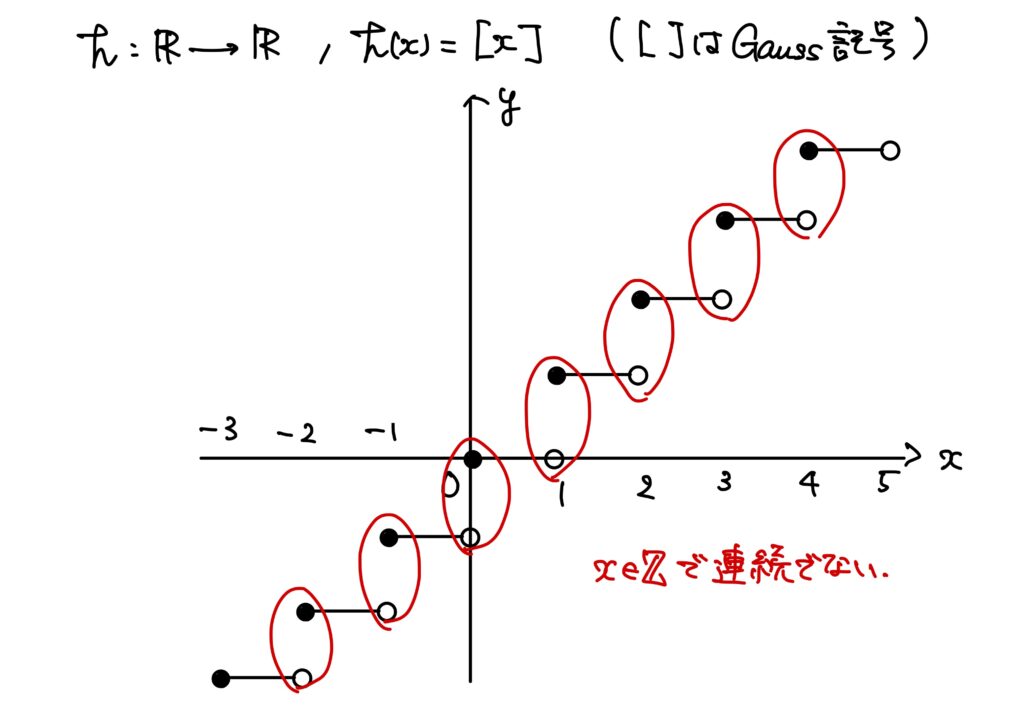
例3.
\(h:\mathbb{R}\to\mathbb{R}\)が\(h(x)=[x]\)([]はGauss記号)とする。
このとき\(h\)は\(x\in\mathbb{Z}\)で連続でない。
ここで、\([x]\)は\(x\)を超えない最大の整数である。
(証明)
示したいことは、
$$(\forall n\in\mathbb{Z})(\exists \epsilon>0)\ {\rm s.t.}\ [(\forall \delta>0)(\exists x\in\mathbb{R})\ {\rm s.t.} 0<|x-n|<\delta \land |h(x)-h(n)|\geq \epsilon]$$
である(\(h\)が\(x=n\in\mathbb{Z}\)で連続であることの否定!)。
つまり、上記を満たすような\(\epsilon>0\)と\(x\in\mathbb{R}\)を見つけてきなさい、ということである。
\(n\in\mathbb{Z}\)とし、\(\epsilon=1\)とする。
また、\(\delta\)を任意の正の実数とする。
このとき、\(x=n-\dfrac{\delta}{2}\)とすると、\(0<|x-n|=\left|-\dfrac{\delta}{2}\right|=\dfrac{\delta}{2}<\delta\)である。 さらに、Gauss記号[]の性質\(x-1<[x]\leq x\)を用いれば、
\begin{eqnarray}
|h(x)-h(n)|&=&\left|\left[ n-\frac{\delta}{2}\right]-n\right|\\
&>&\left|n-\frac{\delta}{2}-1-n\right|\\
&=&\left|-\frac{\delta}{2}-1\right|\\
&=&\frac{\delta}{2}+1>1
\end{eqnarray}
であるので、
$$(\forall n\in\mathbb{Z})(\exists \epsilon>0)\ {\rm s.t.}\ (\forall \delta>0)(\exists x\in\mathbb{R})\ {\rm s.t.} 0<|x-n|<\delta \land |h(x)-h(n)|\geq \epsilon$$
が成り立つ。
従って、\(h\)は\(x=n\ (n\in\mathbb{Z})\)で不連続である。
(Q.E.D.)
例4.について
例4.
\(u:\mathbb{R}\to\mathbb{R}\)が
$$u(x)=\begin{cases}
x+2&(x\in\mathbb{R}\setminus \{1\})\\
1&(x=1)
\end{cases}$$
で定められていたとする。
このとき、\(\displaystyle \lim_{x\to 1}u(x)=3\)だが、\(u(1)=1\)である。
すなわち、\(u\)は\(x=1\)で不連続である。

(証明)
示したいことは
$$(\exists \epsilon>0)\ {\rm s.t.}\ [(\forall \delta>0)(\exists x\in\mathbb{R})\ {\rm s.t.} 0<|x-1|<\delta \land |u(x)-u(1)|\geq \epsilon]$$
である(\(u\)が\(x=1\)で連続であることの否定!)。 つまり、上記を満たすような\(\epsilon>0\)と\(x\in\mathbb{R}\)を見つけてきなさい、ということである。
\(\epsilon=1\)とし、\(\delta\)を任意の正の実数とする。
このとき、\(x=\dfrac{\delta}{2}+1\)とすると、\(0<|x-1|=\left|\dfrac{\delta}{2}+1-1\right|=\dfrac{\delta}{2}<\delta\)である。
また、\(\dfrac{\delta}{2}+1>1\)だから\(\dfrac{\delta}{2}+1\neq1\)である。
従って、
$$|u(x)-u(1)|=\left|u\left(\frac{\delta}{2}+1\right)-u(1)\right|=\frac{\delta}{2}+3-1=\frac{\delta}{2}+2>1=\epsilon$$
であるので、
$$(\exists \epsilon>0)\ {\rm s.t.}\ [(\forall \delta>0)(\exists x\in\mathbb{R})\ {\rm s.t.} 0<|x-1|<\delta \land |u(x)-u(1)|\geq \epsilon]$$
が成り立つ。
従って、\(u\)は\(x=1\)で不連続である。
(Q.E.D.)
関数の連続の言い換え
先に関数の連続は
のだった。
また、定義域のすべての要素\(a\)に対して上記が成り立つとき、定義域内で連続であるというのだった。
これらは結局関数\(f\)の極限が\(f(a)\)と一致するということだった。
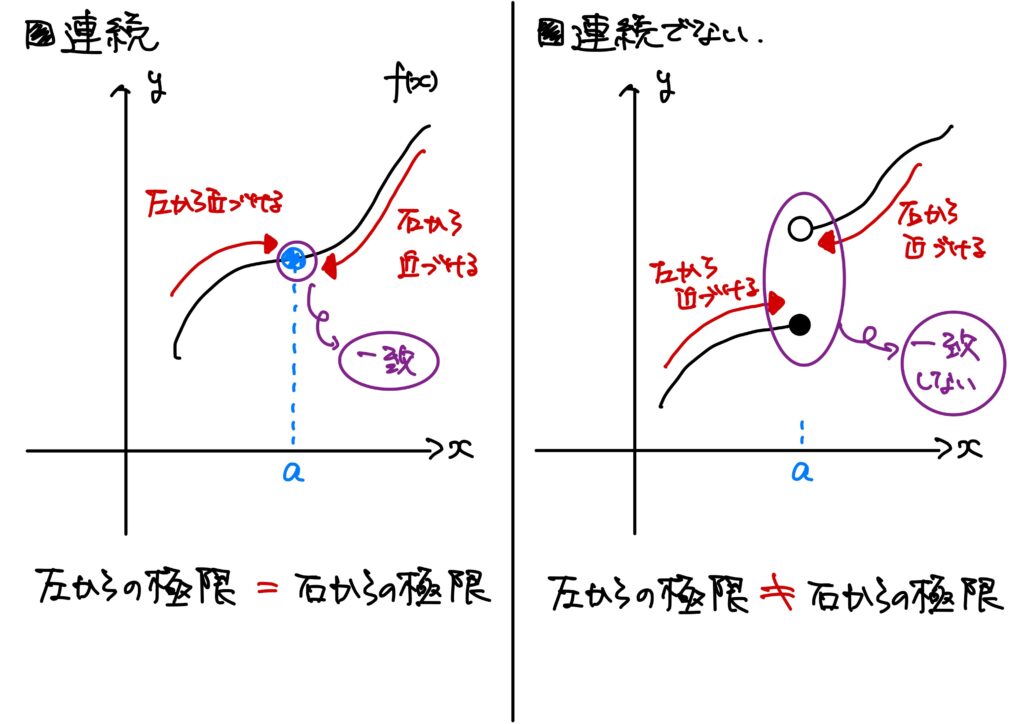
直感的には\(a\)で関数がつながっているときに\(a\)で連続だ、ということだった。
これを言い換えてみると、
近づく方向ってどうやって数学で表現するの?
何ら難しいことではない。
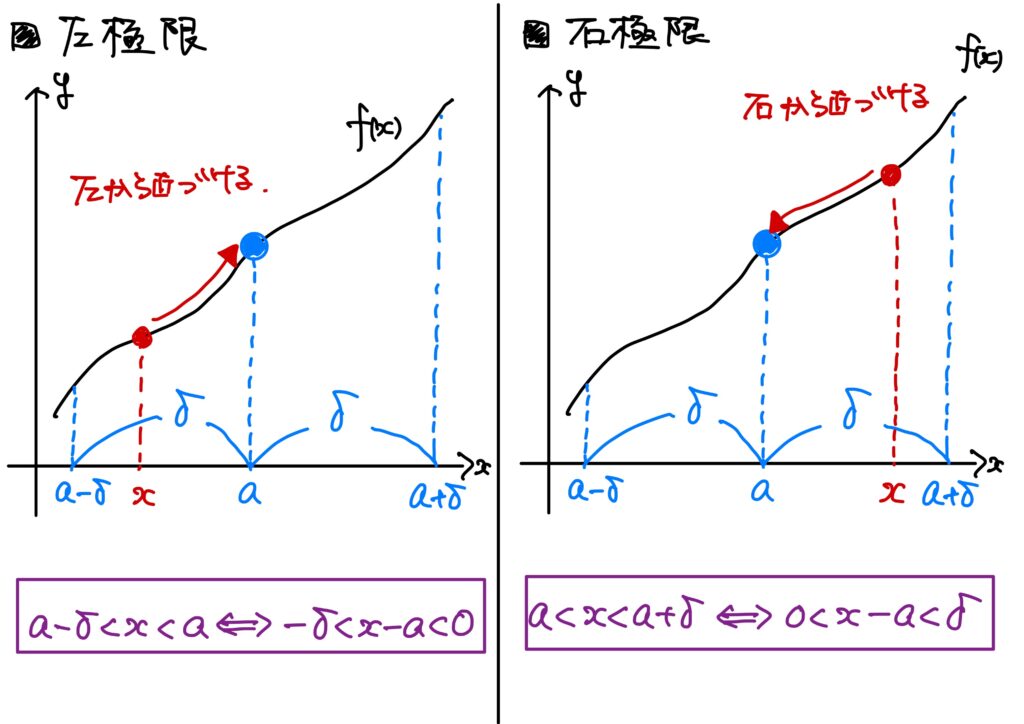
- 右から近づく
右から\(a\in\mathbb{R}\)に近づく、というのは\(x\)が\(a\)よりも大きい状態で\(a\)に近づくということ。 - 左から近づく
左から\(a\in\mathbb{R}\)に近づく、というのは\(x\)が\(a\)よりも小さい状態で\(a\)に近づくということ。
なのである。
関数が\(a\)で連続であるというのは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |f(x)-f(a)|<\epsilon)$$
が成り立つことだった。
近づける方向は\(x\)に対する条件なのだから、\(0<|x-a|<\delta\)の部分を改変することで表現できる。 \(0<|x-a|<\delta\)は\(-\delta\)の状態で近づく。
従って、右から近づくことは\(0<x-a<\delta\)で表現される。
同様に、\(-\delta<x-a<0\)は左から近づくことを表現している。
これを論理式で書けば、次である。
- \(R\)が関数\(f\)の右極限であるとは、 $$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta\Rightarrow |f(x)-R|<\epsilon)$$ が成り立つことをいう。このとき、 $$\lim_{x\to a+0}f(x)=R$$ と書く。
- \(L\)が関数\(f\)の左極限であるとは、 $$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta<x-a<0\Rightarrow |f(x)-L|<\epsilon)$$ が成り立つことをいう。このとき、 $$\lim_{x\to a-0}f(x)=L$$ と書く。
片側極限と関数の連続との関係
では、片側極限がどのように関数の連続と関連するかということを表現する定理を述べる。
(証明)
\(f:I\to\mathbb{R}\)を関数、\(\alpha\in\mathbb{R}\)とする。
- \(\displaystyle\lim_{x\to a}f(x)=\alpha\Rightarrow\lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha\)の証明
示したいことは、
①\(\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta_1\Rightarrow |f(x)-\alpha|<\epsilon_1)\)
②\(\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta_2<x-a<0\Rightarrow |f(x)-\alpha|<\epsilon_2)\)
が成り立つことである。
\(\displaystyle\lim_{x\to a}f(x)=\alpha\)であるから、
$$(\forall \epsilon_0>0)(\exists \delta_0>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta_0\Rightarrow |f(x)-\alpha|<\epsilon_0)$$
が成り立つ。
故に上記を満たす\(\delta_0>0\)を見つけてくることができる。
\(\delta_1\)および\(\delta_2\)として\(\delta\)を採用し、\(\epsilon_0>0\)は任意だっため新たに\(\epsilon\)と書き換えると、\(0<x-a<\delta\)ならば、\(0<|x-a|<\delta\)が成り立つ。
また、\(-\delta<x-a<0\)ならば、\(0<|x-a|<\delta\)が成り立つ。
故に
$$\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta\Rightarrow |f(x)-\alpha|<\epsilon)$$
かつ
$$\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta<x-a<0\Rightarrow |f(x)-\alpha|<\epsilon_2)$$
が成り立つので、①および②が成り立つ。
- \(\displaystyle\lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha\Rightarrow\lim_{x\to a}f(x)=\alpha\)の証明
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |f(x)-\alpha|<\epsilon)$$
である。
今、\(\displaystyle\lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha\)なのだから、
①\(\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta_1\Rightarrow |f(x)-\alpha|<\epsilon_1)\)
②\(\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta_2<x-a<0\Rightarrow |f(x)-\alpha|<\epsilon_2)\)
が成り立っている。
故に上記を満たす\(\delta_1>0,\ \delta_2\)を見つけてくることができる。
\(\delta\)として、\(\delta_1\)と\(\delta_2>0\)の内、大きい方を採用し、\(\epsilon_0>0\)は任意だっため新たに\(\epsilon\)と書き換えると、
①’\(\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta\Rightarrow |f(x)-\alpha|<\epsilon)\)
②’\(\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta<x-a<0\Rightarrow |f(x)-\alpha|<\epsilon)\)
が成り立っている。
従って、\(0<|x-a|<\delta\)ならば\(0<x-a<\delta\)かつ\(-\delta<x-a<0\)が成り立つ。
故に
$$\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |f(x)-\alpha|<\epsilon)$$
が成り立つ。(Q.E.D.)
連続関数の和・差・積・商
関数に対する「連続である」という条件は和をとっても差をとっても積をとっても割っても連続関数である。
「何の役に立つの?」と思うかもしれないが、筆者は非常に有用であると感じている。
筆者が挙げている例はどれも理解しやすいようなるべく明らかな例を挙げたりしているわけだが、実際に関数について考察するときは分かりやすいものばかりではない。
むしろわかりにくく複雑な関数のほうが多い。
そんなとき、その関数を細かく分けて個々が連続であれば全体も連続である、という事が分かるのである。
連続である事がわかると、次回解説する(と思う)中間値の定理や最大値の存在定理が使えることになり、より詳細な関数の特徴を捉えることができる。
本当にそうか?ということを和と差だけ確認してみる。
(※なぜ和と差だけなのか?というのは後述します。)
例1′.+例2′.
- 例1.:\(f:\mathbb{R}\to\mathbb{R}\)、\(f(x)=x^2\)
- 例2.:\(g:\mathbb{R}\to\mathbb{R}\)、\(g(x)=2x\)
だった。
このとき、\(f(x)+g(x)=x^2+2x\)である。
\(f(x)+g(x)\)は\(\mathbb{R}\)で連続である。
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |x^2+2x-a^2-2a|<\epsilon)$$
であれば良い。
任意の\(\epsilon>0\)に対して、\(\delta=-(|a|+1)+\sqrt{(|a|+1)^2+\epsilon}\)とすれば、\(\delta>0\)であり、
\begin{eqnarray}
|x^2+2x-a^2-2a|&=&|x^2-a^2+2(x-a)|\\
&=&|(x+a)(x-a)+2(x-a)|\\
&<&|x-a|(|x+a|+2)\\
&<&|x-a|(|x-a+2a|+2)\\
&\leq&|x-a|(|x+a|+2|a|+2)\\
&<&\delta(\delta +2|a|+2)\\
&=&\delta^2+2(|a|+1)\delta\\
&=&(|a|+1)^2-2(|a|+1)\sqrt{(|a|+1)^2+\epsilon}+(|a|+1)^2+\epsilon\\
&\quad&-2(|a|+1)^2+2(|a|+1)\sqrt{(|a|+1)^2+\epsilon}=\epsilon
\end{eqnarray}
であるから\(f(x)+g(x)\)は\(\mathbb{R}\)で連続である。
例1′.-例2′.
- 例1.:\(f:\mathbb{R}\to\mathbb{R}\)、\(f(x)=x^2\)
- 例2.:\(g:\mathbb{R}\to\mathbb{R}\)、\(g(x)=2x\)
だった。
このとき、\(f(x)-g(x)=x^2-2x\)である。
\(f(x)-g(x)\)は\(\mathbb{R}\)で連続である。
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |x^2-2x-a^2+2a|<\epsilon)$$
であれば良い。
任意の\(\epsilon>0\)に対して、\(\delta=-(|a|-1)+\sqrt{(|a|-1)^2+\epsilon}\)とすれば、\(\delta>0\)であり、
\begin{eqnarray}
|x^2-2x-a^2+2a|&=&|x^2-a^2-2(x-a)|\\
&=&|(x+a)(x-a)-2(x-a)|\\
&<&|x-a|(|x+a|-2)\\
&<&|x-a|(|x-a+2a|-2)\\
&\leq&|x-a|(|x+a|+2|a|-2)\\
&<&\delta(\delta +2|a|-2)\\
&=&\delta^2+2(|a|-1)\delta\\
&=&(|a|-1)^2-2(|a|-1)\sqrt{(|a|-1)^2+\epsilon}+(|a|-1)^2+\epsilon\\
&\quad&-2(|a|-1)^2+2(|a|-1)\sqrt{(|a|-1)^2+\epsilon}=\epsilon
\end{eqnarray}
であるから\(f(x)-g(x)\)は\(\mathbb{R}\)で連続である。
このように、和と差については正しそうだ、という事が分かった。
実は、積、商についても成り立つ。
つまり、以下が成り立つ。
- \(a\in I\)とし、\(f\)と\(g\)は\(a\)で連続とするとき、次が成り立つ。
- \(f(x)+g(x)\)、\(f(x)-g(x)\)、\(f(x)g(x)\)は\(a\)で連続である。すなわち、
- \(\displaystyle \lim_{x\to a}(f(x)+g(x))=f(a)+g(a)\),
- \(\displaystyle \lim_{x\to a}(f(x)-g(x))=f(a)-g(a)\),
- \(\displaystyle \lim_{x\to a}(f(x)g(x))=f(a)g(a)\).
- \(\displaystyle g(a)\neq 0\)ならば、\(\dfrac{f(x)}{g(x)}\)は\(a\)で連続である。すなわち、 $$\lim_{x\to a}\dfrac{f(x)}{g(x)}=\dfrac{f(a)}{g(a)}$$ である。
- \(f(x)+g(x)\)、\(f(x)-g(x)\)、\(f(x)g(x)\)は\(a\)で連続である。すなわち、
- \(f\)と\(g\)は\(I\)で連続であるとするとき、次が成り立つ。
- \(f(x)+g(x)\)、\(f(x)-g(x)\)、\(f(x)g(x)\)は\(I\)で連続である。すなわち、
- \(\displaystyle(\forall a\in I) \lim_{x\to a}(f(x)+g(x))=f(a)+g(a)\),
- \(\displaystyle(\forall a\in I) \lim_{x\to a}(f(x)-g(x))=f(a)-g(a)\),
- \(\displaystyle(\forall a\in I) \lim_{x\to a}(f(x)g(x))=f(a)g(a)\).
- \(\displaystyle g(a)\neq 0\)ならば、\(\dfrac{f(x)}{g(x)}\)は\(I’=\{x\in\mid g(x)\neq 0\}\)で連続である。すなわち、 $$(\forall a\in I’)\ \lim_{x\to a}\dfrac{f(x)}{g(x)}=\dfrac{f(a)}{g(a)}$$ である。
- \(f(x)+g(x)\)、\(f(x)-g(x)\)、\(f(x)g(x)\)は\(I\)で連続である。すなわち、
実はこの定理はすでに証明している。
というのも、以下をすでに証明しているからである。
\(I\)を\(\mathbb{R}\)の区間、\(f:I\to\mathbb{R}\)および\(g:I\to\mathbb{R}\)を関数、\(a\in\bar{I}\)、\(A,b\in\mathbb{R}\)とし、\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)とする。 このとき、次が成り立つ。
- \(\displaystyle \lim_{x\to a}(f(x)+g(x))=\lim_{x\to a}f(x)+\lim_{x\to a}g(x)=A+B\),
- \(\displaystyle \lim_{x\to a}(f(x)-g(x))=\lim_{x\to a}f(x)-\lim_{x\to a}g(x)=A-B\),
- \(\displaystyle \lim_{x\to a}f(x)g(x)=\left(\lim_{x\to a}f(x)\right)\cdot\left(\lim_{x\to a}g(x)\right)=AB\),
- \(B\neq0\)ならば、\(\delta_0>0\)が存在して、\(|x-a|<\delta_0\)なる\(x\in I\)に対して、\(g(x)\neq 0\)で、\(\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\displaystyle\lim_{x\to a}f(x)}{\displaystyle\lim_{x\to a}g(x)}=\frac{A}{B}\)
この事実において、\(\forall a\in I\)に対して\(A=f(a)\)かつ\(B=g(a)\)のときを考えれば良いからである。
そういう意味で、積、商についての例を省いた。
結
今回は関数の連続について説明した。
関数の連続は一言で言えば、つながっている、ということで
要は、
というわけである。
この\(a\)が\(f\)の定義域の任意の要素であっても成り立つ場合には、定義域内で連続であるという。
また、関数の連続は左右極限が一致し、かつその点においての関数の極限と一致するという捉え方もできる。
さらに、連続関数を四則演算で組み合わせた関数もまた連続関数である。
次回は合成関数、多項式関数、有理関数の連続について述べる。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!




コメントをする