「多項式関数と有理関数は連続な関数」【解析学の基礎シリーズ】関数の極限編 その8

本記事の内容

本記事は多項式関数と有理関数が$\mathbb{R}$で連続な関数であることを説明する記事である。

本記事を読むにあたり、関数の連続について知っているとより理解が進むと思われるので、その際は以下の記事を参照してください。

「関数の連続って数学的に何？」「実際に証明してみよう！」【解析学の基礎シリーズ】関数の極限編 その５

...

for-spring.com

2022.04.05

多項式関数は$\mathbb{R}$で連続な関数

多項式という言葉は恐らく中学数学で出現すると思われる。
多項式関数というのはその関数バージョンである。
つまり、$y=x^2+2x+2$ような関数のことを多項式関数という。
「まあ、雰囲気は分かるよ」という感じだと思われるので、早速「多項式関数とは何か？」ということについて述べてしまう。

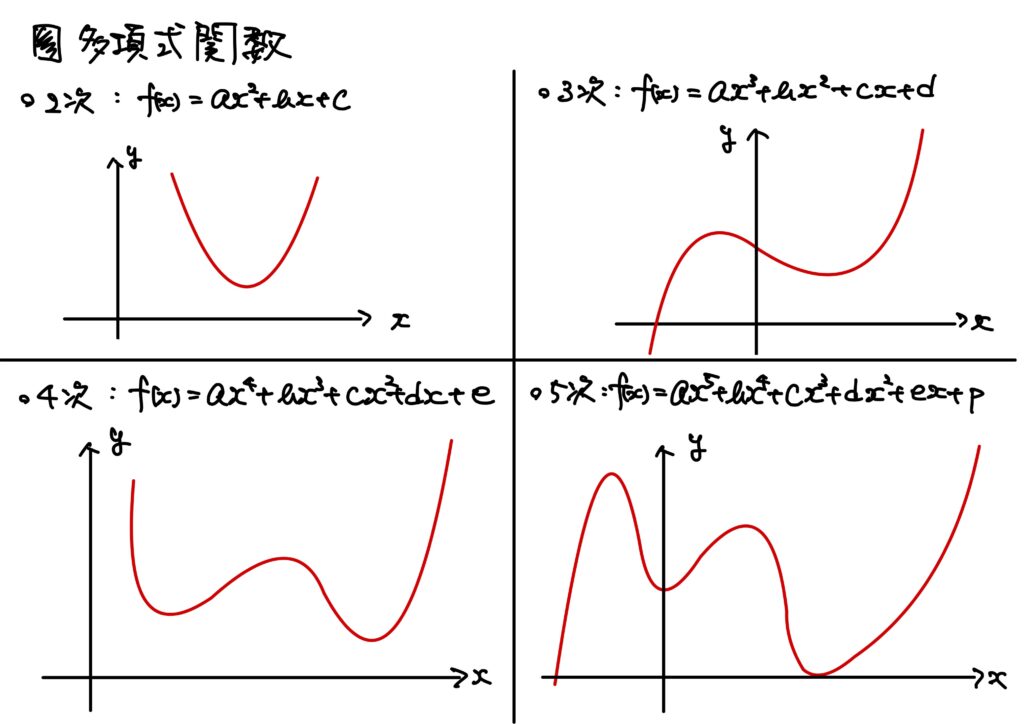
ちなみに整数係数多項式と言われると、$x^3+4x^2+3$のような式である。
係数として$\pi$なども許すというのが実係数多項式である。
勿論、整数係数多項式は実係数多項式である。

この多項式関数は連続である。
「本当かよ」と思うかもしれないので、簡単ではあるが、2つの例を挙げる。

(※実は前回すでに証明しているので、「それ知ってる」という方は読み飛ばしてください。)

例1.
$f:\mathbb{R}\to\mathbb{R}$が$f(x)=2x$で定められているとする。
このとき、$f$は$\mathbb{R}$で連続である。

(証明)
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
である。 つまり、任意の$\epsilon>0$に対して上記を満たすような$\delta>0$を見つけてきなさい、ということである。
$\delta=\frac{\epsilon}{2}$とすると、$\delta>0$である。
$0<|x-a|<\delta$を満たす$x\in\mathbb{R}$に対して、
$$|2x-2a|=2|x-a|<2\delta=2\cdot\frac{\epsilon}{2}=\epsilon$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
が成り立ったので、$f$は$\mathbb{R}$で連続である。
(Q.E.D.)

例2.
$g:\mathbb{R}\to\mathbb{R}$が$g(x)=x^2$で定められているとする。
このとき、$g$は$\mathbb{R}$で連続である。

(証明)
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
である。
つまり、任意の$\epsilon>0$に対して上記を満たすような$\delta>0$を見つけてきなさい、ということである。
$\delta=-|a|+\sqrt{|a|^2+\epsilon}$とすると、$\delta>0$である。
$0<|x-a|<\delta$を満たす$x\in\mathbb{R}$に対して、
$$\begin{eqnarray} |x^2-a^2|&=&|(x+a)(x-a)|\\ &=&|x-a+2a|\cdot|x-a|\leq |x-a|^2+2|a|\cdot|x-a|\\ &=&|a|^2-2|a|\sqrt{|a|^2+\epsilon}+|a^2|+\epsilon+2|a|(-|a|+\sqrt{|a|^2+\epsilon})\\ &=&2|a|^2-2|a|^2+2|a|\sqrt{|a|^2+\epsilon}-2|a|\sqrt{|a|^2+\epsilon}+\epsilon=\epsilon \end{eqnarray}$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |x^2-a^2|<\epsilon)$$
が成り立ったので、$f$は$\mathbb{R}$で連続である。
(Q.E.D.)

例に挙げた通り、多項式関数は連続である。
すなわち、次が成り立つ。

実は、この命題の証明は関数の和・差・積・商の連続性を使うことですぐ終わる。
関数の和・差・積・商の連続性は次であった。

これと「恒等写像は連続である。」、「定数関数は連続である。」という事実を使えば、すぐに終わる。
教科書を書くレベルならものの3行で終わるほどである。
しかし、本記事はなるべく丁寧にをモットーの１つとしているので、少々長くなるが。
(くどいと言われてしまうかもしれないネ)

(命題3.の証明)
$f:\mathbb{R}\to\mathbb{R}$を多項式関数とする。
すなわち、
$$f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_2x^2+a_1x+a_0\quad(n\in\mathbb{N}\cup\{0\},\ a_i\in\mathbb{R})$$
とする。
次の2つの事実を使う。

(命題4.の証明)
$g:\mathbb{R}\to\mathbb{R}$を恒等写像、すなわち任意の$x\in\mathbb{R}$に対して、$g(x)=x$とする。
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}\ 0<|x-a|<\delta\Rightarrow |g(x)-a|<\epsilon)$$
である。
つまり、上記を満たす$\delta>0$を見つけてくれば良い。
$\delta$として任意の正数$\epsilon$を採用する。
$a\in\mathbb{R}$のとき、$0<|x-a|<\delta$なる$x\in\mathbb{R}$に対して、
$$|g(x)-a|=|x-a|<\delta=\epsilon$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}\ 0<|x-a|<\delta\Rightarrow |h(x)-a|<\epsilon)$$
が成り立ったため、恒等写像は$\mathbb{R}$で連続である。
(Q.E.D.)

(命題5.の証明)
$h:\mathbb{R}\to\mathbb{R}$を定数関数、すなわち任意の$x\in\mathbb{R}$に対して、$h(x)=c\ (c\in\mathbb{R})$とする。
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}\ 0<|x-a|<\delta\Rightarrow |h(x)-c|<\epsilon)$$
である。
つまり、上記を満たす$\delta>0$を見つけてくれば良い。
$\delta$として任意の正数$\epsilon$を採用する。
$a\in\mathbb{R}$のとき、$0<|x-a|<\delta$なる$x\in\mathbb{R}$に対して、
$$|g(x)-c|=|c-c|=0<\delta=\epsilon$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}\ 0<|x-a|<\delta\Rightarrow |h(x)-c|<\epsilon)$$
が成り立ったため、定数関数は$\mathbb{R}$で連続である。
(Q.E.D.)

命題3.の証明に戻る。
命題4.と連続関数の和・差・積・商の3.により、$f_1(x)=a_1x\ (\forall a_1\in\mathbb{R})$で定められる関数$f_1:\mathbb{R}\to\mathbb{R}$は$\mathbb{R}$で連続である。
同様に、$f_2(x)=a_2x^2\ (a_2\in\mathbb{R})$で定められる関数$f_2:\mathbb{R}\to\mathbb{R}$も$\mathbb{R}$で連続である。
この操作を繰り返し行うことによって、任意の$n\in\mathbb{N}\cup\{0\}$に対して、$f_n(x)=a_nx^n$で定められる$f_n:\mathbb{R}\to\mathbb{R}$は$\mathbb{R}$で連続であることが分かる。
ここで、連続関数の和・差・積・商の1.により、連続関数は和をとっても連続であるので、$f_0(x)+f_1(x)+\cdots+f_n(x)+f_n(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_2x^2+a_1x+a_0$もまた$\mathbb{R}$で連続である。
従って、多項式関数は$\mathbb{R}$で連続である。
(Q.E.D.)

命題4.と命題5.の証明も与えたという意味で長くなってしまったけど、命題3.の証明自体はすぐ終わった。
勿論、連続関数の和・差・積・商の事実を用いなくても証明は可能である。
とはいえ、結構骨は折れる。

有理関数は$\mathbb{R}$で連続な関数

多項式関数がわかれば、有理関数もすぐ分かる。
というのも、平たく言えば、有理関数というのは分母分子が共に多項式関数であるような関数のことを指すからである。
しかし、注意が必要である。
というのも、「分母は$0$でない」という条件が必要だからである。

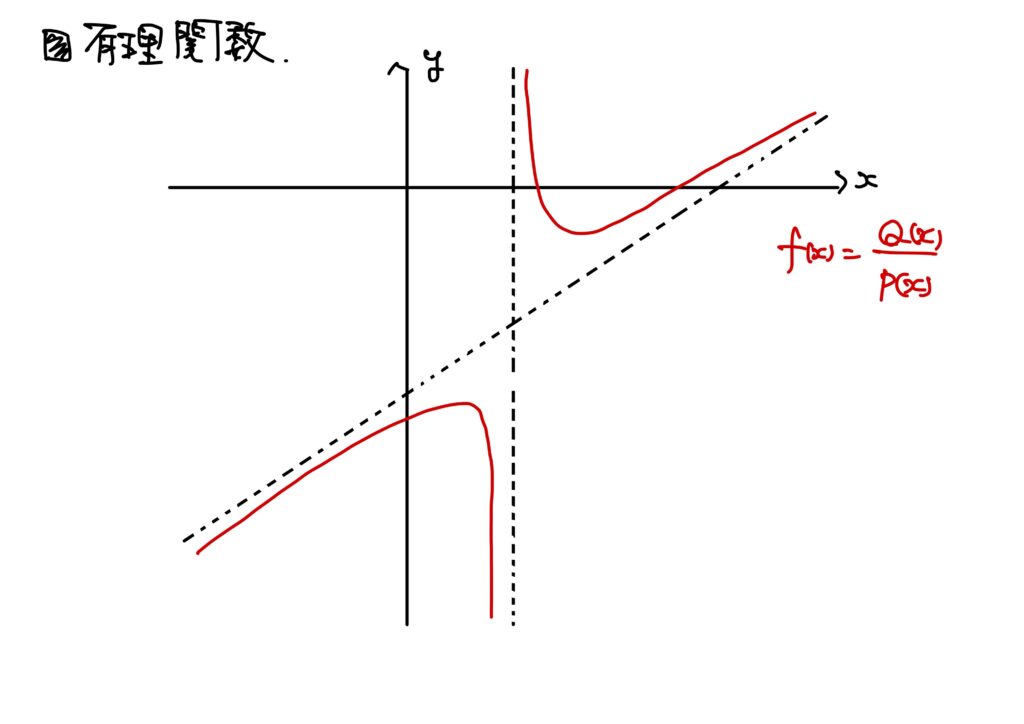
この有理関数は連続である。
「本当かよ」と思うかもしれないので、簡単ではあるが、例を挙げる。

例6. $f:\mathbb{R}\setminus\{0\}\to\mathbb{R}$が$f(x)=\dfrac{x^2-2x+1}{2x}$で定められているとする。
このとき、$f$は$\mathbb{R}\setminus\{0\}$で連続である。

このように有理関数は連続である。
すなわち、次が成り立つ。

(証明)
これも、関数の和・差・積・商の商の事実から直ちに証明できる。

$f:\mathbb{R}\to\mathbb{R}$を有理関数とする。
このとき、$f$は多項式関数$P(x)\neq0$と$Q(x)$を用いて、$f(x)=\dfrac{Q(x)}{P(x)}$と書ける。
$P(x)$と$Q(x)$は多項式関数なのだから、$\mathbb{R}$で連続である。
従って、連続関数の商から$f$は$\{x\in\mathbb{R}\mid P(x)\neq 0\}$で連続である。
(Q.E.D.)

まとめると…

これまでのことをまとめると、

が成り立つ、ということである。

結

今回は、多項式関数と有理関数が$\mathbb{R}$で連続な関数であるということを説明し、証明した。

これらは関数の和・差・積・商の極限からほぼ直ちに導かれる事実である。

次回は連続な関数の合成関数もまた連続な関数である、ということを説明し、証明する。

乞うご期待！質問、コメントなどお待ちしております！

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ１冊持っておくと良いと思います！