本記事の内容
本記事は中間値の定理のイメージを説明する記事です。
本記事を読むにあたり、関数の連続とはどういうことかを知っているとよりイメージが湧きやすいと思われますので、その際は以下の記事を参照してください。
関数の連続性のイメージの復習
関数の連続性のイメージは【解析学の基礎シリーズ】関数の極限編 その4で説明したとおり、
ということでした。
関数が(閉区間で)”つながっている”ことで得られる事実が「中間値の定理」なのです。
※関数の連続性の数学的な説明は【解析学の基礎シリーズ】関数の極限編 その5を御覧ください。
では早速中間値の定理のイメージを説明します。
例と共にに見る中間値の定理のイメージ
中間値の定理はどういう主張なのか、ということを説明する前にまずどういう状況を考え、どういうことが言えそうか(つまり、どういう発想で中間値の定理が成り立つと予想されたか)を説明します。
例
例1.\(\displaystyle f_1:\left[ -\frac{\pi}{2},\frac{5}{2}\pi \right]\to\mathbb{R}\)、\(f_1(x)=\sin x\)
前回の記事(【解析学の基礎シリーズ】関数の極限編 その12)で述べたとおり、この関数は\(\displaystyle \left[ -\frac{\pi}{2},\frac{5}{2}\pi \right]\)で連続です。
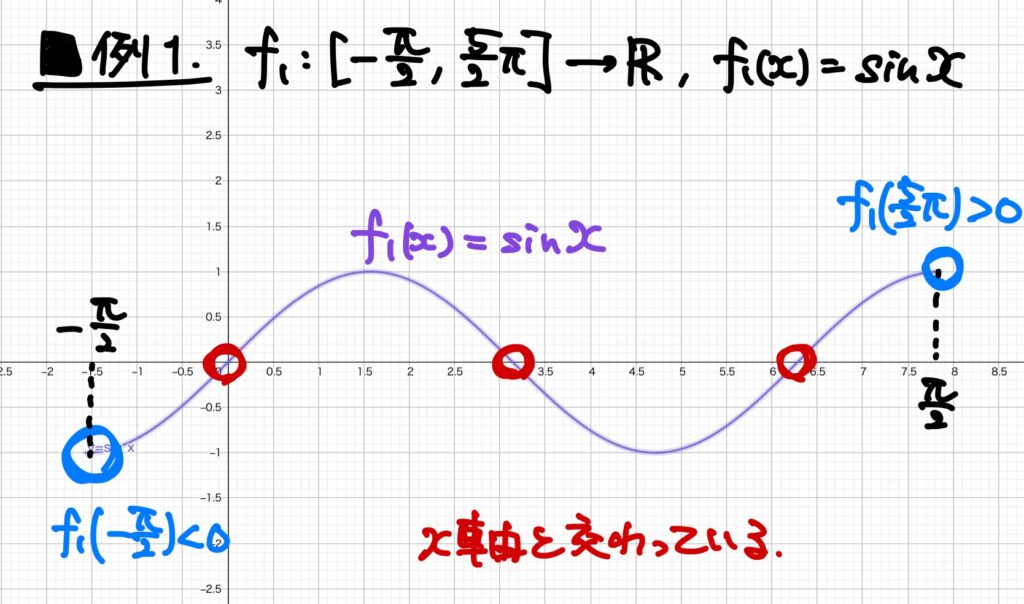
この図において、区間の端点の正負を見てみると
- \(\displaystyle f_1\left(\frac{\pi}{2}\right)=-1<0\)、
- \(\displaystyle f_1\left(\frac{5}{2}\pi\right)=1>0\)
です。
このとき、この関数\(f_1\)は必ず\(x\)軸と交わります。
例2.\(f_2:[0,5]\to\mathbb{R}\),
$$f_2(x)=\begin{cases}
x+2 & (1\leq x\leq 5)\\
x-3 & (0\leq x<1)
\end{cases}
$$
この関数は連続ではありません(証明はしませんが、似たような関数が連続でないことの証明は【解析学の基礎シリーズ】関数の極限編 その5で与えているので、そちらを参照してください)。
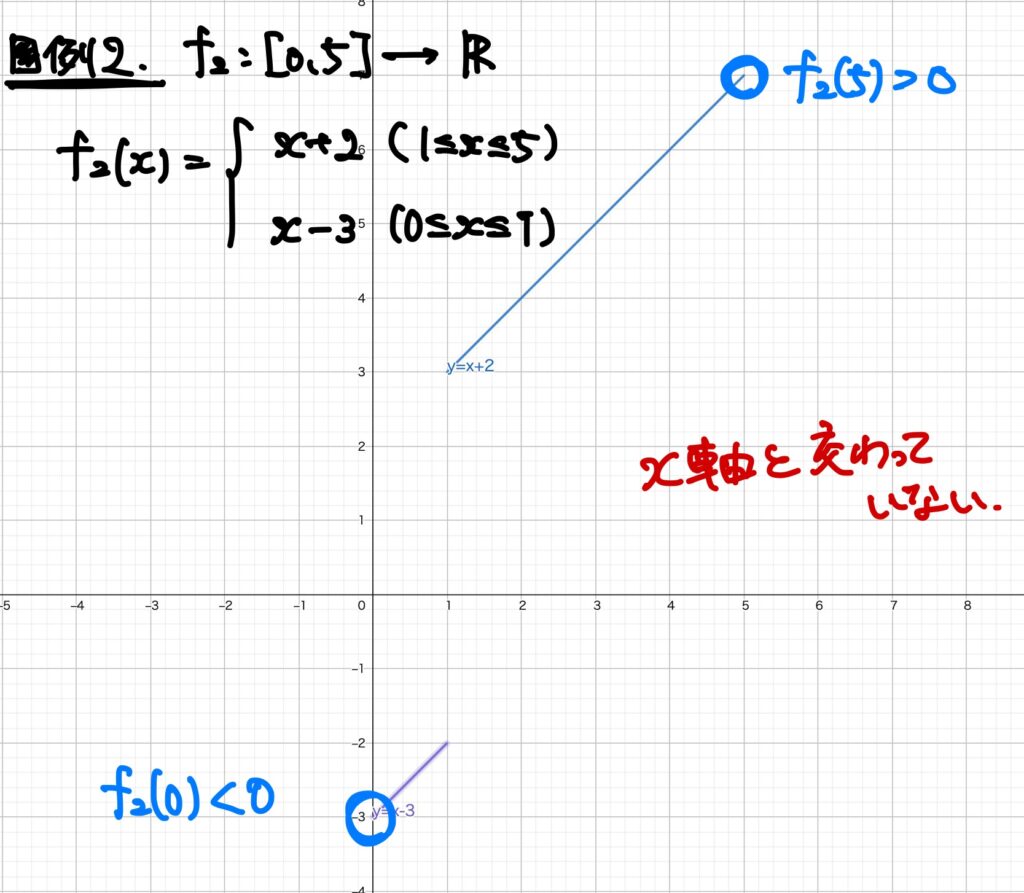
この図において、区間の端点の正負を見てみると
- \(f_2(0)=-3<0\)、
- \(f_2(5)=7>0\)
です。
このとき、この関数\(f_1\)は\(x\)軸とは交わりません。(ポイント!)
このように、連続な関数に対して、定義域の端点の符号が異なれば、その関数は必ず\(x\)軸と交わる、ということなのです。
これが中間値の定理です。
より直感的な説明を以下で行います。
中間値の定理のイメージ図
「つまり、中間値の定理ってどういうことなのか?」ということを説明する図が以下にあります。
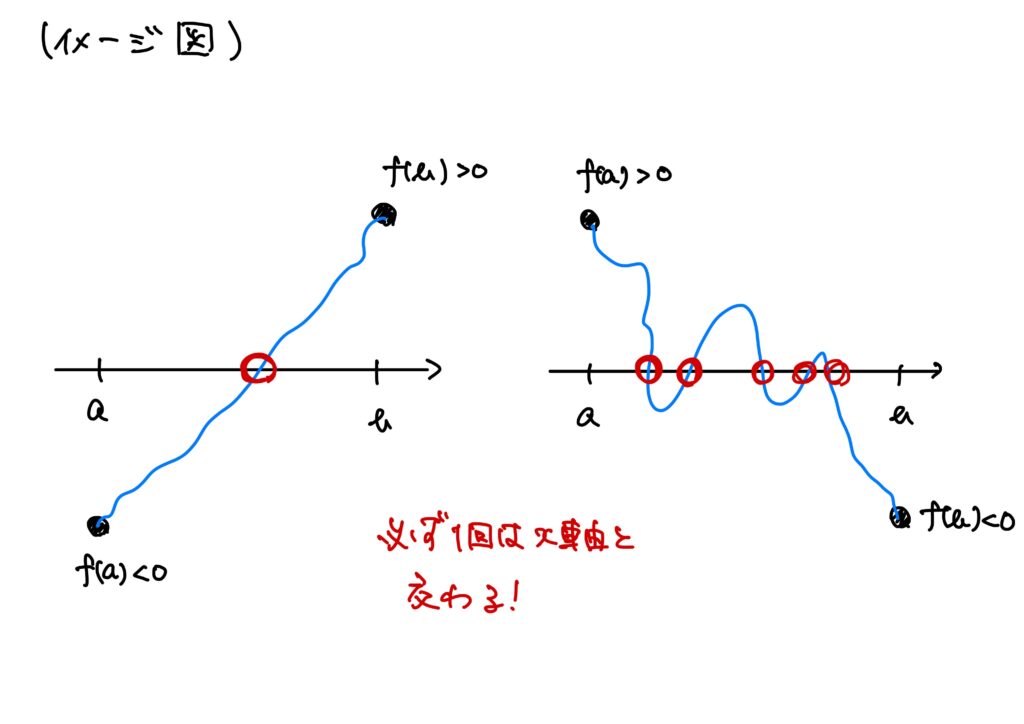
このように、途切れることなくつないだとき、つないだ線は必ず1回は絶対に\(x\)軸と交わります。
この「途切れることなくつないだとき」が関数の連続性に対応します。
連続でない関数については、例2.で見たとおり、端点の値が異符号でも必ず\(x\)軸と交わるわけではありません。
連続であるという条件は「閉区間で」という条件が付きます。
なぜかを以下で説明します。
中間値の定理のポイント
以上のことをまとめると、中間値の定理はイメージで言うと次のような主張です。
ということです。
ここで、「開区間じゃダメなの?」と思うかもしれません。
実はダメなんです。
変な例ですが、こんな例を考えてみます。
例3. \(f_3:[1,2]\to\mathbb{R}\),
$$f_3(x)=\begin{cases}
-x & (1<x<2)\\
-2 & (x=1)\\
1 & (x=2)
\end{cases}
$$
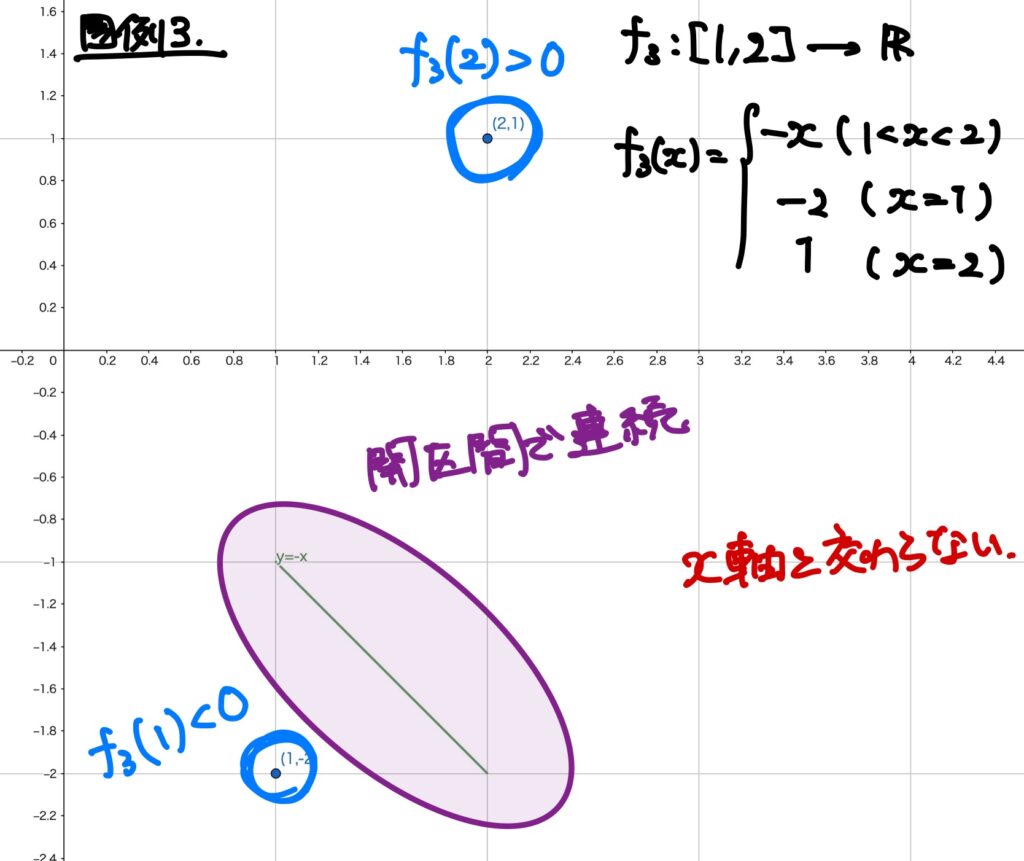
この関数\(f_3\)は開区間\((1,2)\)で連続です。
さらに、
- \(f_3(1)=-2<0\)、
- \(f_3(2)=1>0\)
であるので、閉区間での端点は異符号です。
しかしながら、この関数は\(x\)軸とは交わりません。
このように、開区間で連続で、その端点での関数の値が異符号だったとしても、\(x\)軸と必ず交わるわけではないのです。
結
今回は中間値の定理のイメージを説明しました。
中間値の定理のイメージとしては、
ということで、閉区間で連続じゃないとダメだよ、ということも注意しました。
主観ですが、筆者が最初のこの定理を見たときに「当たり前じゃね?」と思いました。
また同時に「こんな当たり前のことをどう証明するんだ?」とも思いました。
次回は中間値の定理を数学的に明示して、さらに証明も与えます。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!




コメントをする