本記事の内容
本記事は、部分群の対応に関する準同型定理について解説する記事です。
本記事を読むにあたり、正規部分群、自然な写像、商群(剰余群)について知っている必要があるため、以下の記事も合わせてご覧ください。
↓正規部分群の記事
↓自然な写像、商群(剰余群)の記事
部分群の対応に関する準同型定理の明示
まず、主張を明示します。
定理1.(準同型定理(部分群の対応))
\(N\)を群\(G\)の正規部分群、\(\pi:G\longrightarrow G/{N}\)を自然な準同型とする。\(G/{N}\)の部分群の集合を\(\mathbb{X}\)、\(G\)の\(N\)を含む部分群の集合を\(\mathbb{Y}\)とするとき、写像 $$ \varphi:\mathbb{X}\ni H\mapsto \pi^{-1}(H)\in\mathbb{Y},\quad \psi:\mathbb{Y}\ni K\mapsto \pi(K)\in\mathbb{X} $$ は互いに逆写像である。従って、集合\(\mathbb{X},\mathbb{Y}\)は1対1対応する。何が言いたい定理なんですか?
要するに、
ということです。
より具体的な話は後述します。
部分群の対応に関する準同型定理の証明
では証明します。
定理1.の証明
①\(\varphi\)と\(\psi\)がwell-definedであることの証明
\(H\in \mathbb{X}\)ならば、\(1_{G/{N}}\in H\)なので、\(N=\pi^{-1}(1_{G/{N}})\subset \pi^{-1}(H)\)です。
特に、\(1\in\pi^{-1}(H)\)です。
\(x,y\in \in\pi^{-1}(H)\)なら、\(\pi(xy)=\pi(x)\pi(y)\in H\)なので、\(xy\in\pi^{-1}(H)\)です。
同様にして、\(x^{-1}\in\pi^{-1}(H)\)となるので、\(\pi^{-1}(H)\)は\(G\)の部分群です。
従って、\(\pi^{-1}(H)\in\mathbb{Y}\)となり、\(\varphi\)は写像として体裁が整っています(これをwell-definedというのでした)。
\(K\subset G\)が\(N\)を含む部分群であれば、任意の\(g\in G\)に対して\(gNg^{-1}\subset N\)なので、この条件は\(g\in K\)に対しても成り立ちます。
従って、\(N\triangleleft K\)、すなわち\(N\)は\(K\)の正規部分群です。
\(K/{N}\)は\(K\)の要素\(g\)により\(gN\)という形をした剰余類の集合ですので、\(G/{N}\)の部分集合とみなすことが出来、\(K/{N}=\pi(K)\)です。
故に、\(\pi(K)\in \mathbb{X}\)となるため、\(\psi\)もwell-definedです。
②\(\left(\varphi\circ \psi\right)(K)=K\)の証明
\(K\in\mathbb{Y}\)であれば、\(H=\pi(K)\)とおくと、\(K\subset \pi^{-1}(H)\)です。
\(g\in\pi^{-1}(H)\)なら、\(\pi(g)\in\pi(K)\)です。
故に、\(h\in K\)が存在して、\(\pi(g)=\pi(h)\)です。
これは、\(gN=hN\)、つまり\(n\in N\)が存在して\(g=hn\)であることを意味しています。
\(N\subset K\)であるので\(g\in K\)です。
従って、\(K=\pi^{-1}(H)\)となり、\(\left(\varphi\circ \psi\right)(K)=K\)です。
ここで、\(K\)は\(G\)の部分集合ですが、等式\(\left(\varphi\circ \psi\right)(K)=K\)では\(K\)を\(\mathbb{Y}\)の一つの要素とみなしていることに注意です。
③\(\varphi\)と\(\psi\)が互いに逆写像であることの証明
\(H\in\mathbb{X}\)ならば、\(\pi\left( \pi^{-1}(H)\right)\subset H\)です。
\(h\in H\)ならば、\(\pi\)は全射なので、\(g\in G\)が存在して、\(\pi(g)=h\in H\)です。
これは、\(g\in\pi^{-1}(H)\)であることを意味しています。
故に、\(h=\pi(g)\in\pi\left( \pi^{-1}(H)\right)\)です。
従って、\(H\subset\pi\left( \pi^{-1}(H)\right)\)となり、\(\left( \psi\circ \varphi\right)(H)=\pi\left( \pi^{-1}(H)\right)=H\)です。
定理1.の証明終わり
結局何が言いたいんですか?(例から見てみます)
正六角形に対する合同変換全体が成す群\(D_6\)を考えます。
状況をクリアにするために、ここでは正六角形の中心が二次元ユークリッド空間の原点にあり、2つの互いに反対側に位置する頂点がx軸上に乗っているとします。
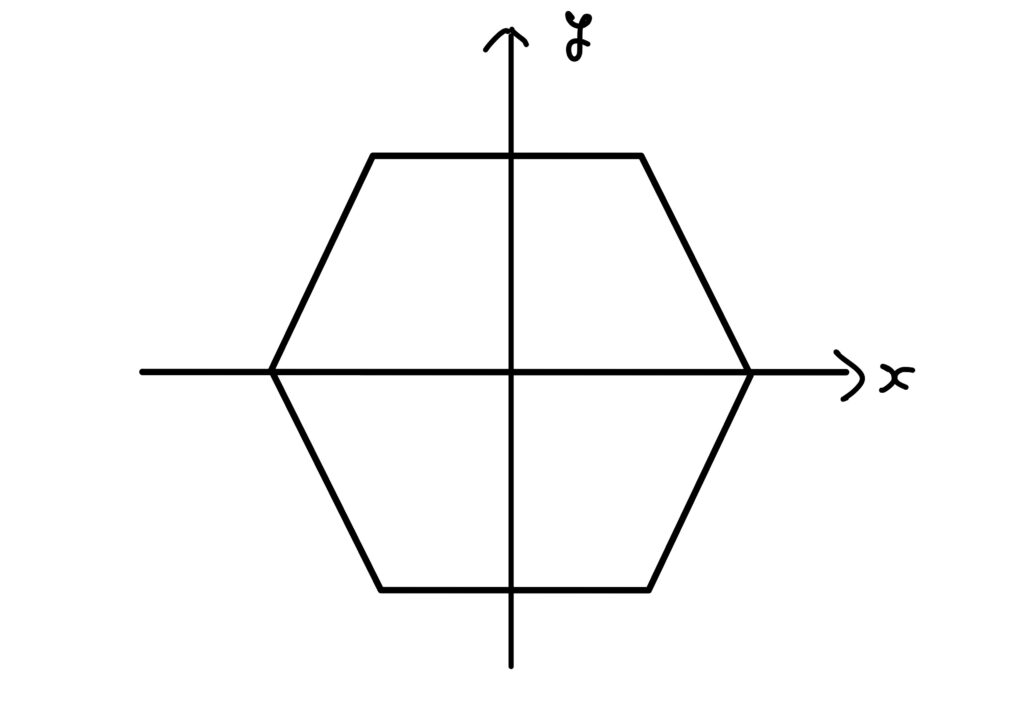
\(D_6\)は回転と鏡像反転の操作によって生成されます。
ここでは原点を中心に半時計回りの方向に\(\displaystyle\frac{\pi}{3}\)回転する操作を\(\sigma\)、\(x\)軸に対して反転する操作を\(\tau\)と呼ぶことにします。
すると、\(D_6\)の要素は以下のように表すことができます。
$$
\left\{e,\ \sigma,\ \sigma^2,\ \sigma^3,\ \sigma^4,\ \sigma^5,\ \tau\ \tau\sigma,\ \tau\sigma\ \tau\sigma^2\ \tau\sigma^3\ \tau\sigma^4\ \tau\sigma^5\right\}
$$
次に、正規部分群を一つ選んでみます。
ここでは、\(N=\left\{e,\ \sigma^2,\ \sigma^4\right\}\)としてみます。
このとき、群\(N\)に関する\(D_6\)のp同値類は以下のように分類されます。
\begin{eqnarray}
&&N=\left\{e,\ \sigma^2,\ \sigma^4\right\},\\
&&\sigma N=\left\{\sigma,\ \sigma^3,\ \sigma^5\right\},\\
&&\tau N=\left\{\tau,\ \tau\sigma^2,\ \tau\sigma^4\right\},\\
&&\tau\sigma N=\left\{\tau\sigma,\ \tau\sigma^3,\ \tau\sigma^5\right\}
\end{eqnarray}
これらが\(D_{6}\)の要素の元になります。
つまり、
$$
D_6/{N}=\left\{N,\ \sigma N,\ \tau N,\ \tau\sigma N\right\}
$$
となります。
ここで、単位元は\(N\)です。
\(D_6/{N}\)は以下の5つの部分群が存在します。
\begin{eqnarray}
&&X_0=\left\{N\right\},\\
&&X_1=\left\{N,\ \sigma N\right\},\\
&&X_2=\left\{N,\ \tau N\right\},\\
&&X_3=\left\{N,\ \tau\sigma N\right\},\\
&&X_4=D_6/{N}
\end{eqnarray}
これで剰余群の部分群が分かりました。
続いて、これらと一対一に対応する\(D_6\)の部分群を求めてみます。
部分群に対する準同型定理によれば、それは\(N\)を含む部分群になります。
例えば、
\begin{eqnarray}
&&Y_0=N\\
&&Y_1=\left\{e,\ \sigma,\ \sigma^2,\ \sigma^3,\ \sigma^4,\ \sigma^5\right\},\\
&&Y_2=\left\{e,\ \sigma^2,\ \sigma^4,\ \tau,\ \tau\sigma^2,\ \tau\sigma^4\right\},\\
&&Y_3=\left\{e,\ \sigma^2,\ \sigma^4,\ \tau\sigma,\ \tau\sigma^3,\ \tau\sigma^5\right\},\\
&&Y_4=D_6
\end{eqnarray}
ここで、\(N\)の要素について見てみると、\(N\)は要するに偶数回の回転操作のみを集めた部分群となっています。
そこから得られる剰余類は\(\sigma N\)は奇数回の回転操作、\(\tau N\)は反転した状態での偶数回の回転操作、そして\(\tau \sigma N\)は反転した状態での奇数回の回転操作を表しています。
ここまでくれば、商群\(D_6/{N}\)の要素が表しているものが明確になると思います。
この剰余群は偶数回の回転操作の集まり\(N\)で割ることによって得られるので、偶数回の回転操作を全て同一視していることになります。
すなわち、「\(0\)回転だろうが\(2\)回転だろうが\(4\)回転だろうが、結局どれも偶数回の回転操作なんでしょ?細かい回転数は無視してまとめて考えてようよ。」ということです。
そのため、\(D_6/{N}\)の要素は具体的な回転数を無視した、\(\{\)偶数回転、奇数回転、反転偶数回転、反転奇数回転\(\}\)という抽象的な操作の集まりから成る群だ、と考えることが出来るわけです。
そうした時に、例えば\(X_1\)というのは偶数回転と奇数回転を合わせたものになっているし、\(X_2\)は偶数回転と反転偶数回転を合わせたものになっています。
また、\(Y_1\)は具体的に偶数回転と奇数回転を表す元を全て寄せ集めたものになっており、\(Y_2\)は偶数回転と反転偶数回転を表す元の寄せ集めになっています。
これらの関係を図示すると、次です。
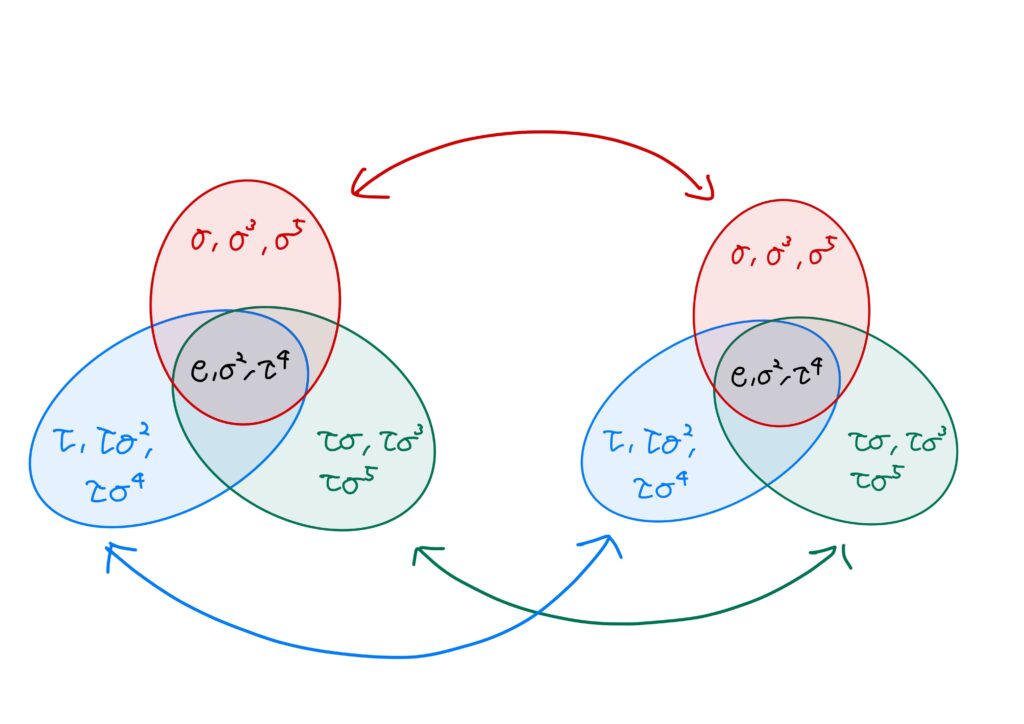
これではっきりしたのではないでしょうか。
皆様のコメントを下さい!
今日はライプニッツです。
ライプニッツ(Leibniz, Gottfried Wilhelm;1646-1716)は法学、言語学、神学など広範な 主題に及ぶ著述を行った万能人です。
ライプツィヒに生まれ、6歳のときに亡くした父親から哲学・神学の蔵書を受け継ぎ、その読破のために 12歳までにラテン語を完全にマス ターしました。
14歳でライプツィヒ大学に入学し、2年後に卒業して1664年に法哲学の論文で学位を取得しました。
ハノーヴァーの王室で外交顧問および図書館長として仕えました。
1700年にベルリンに赴き、科学アカデミー の創設に参加、初代総裁に就任しています。
外交官としては、30年戦争(ボヘミアにおける新教徒の反乱がきっかけとなって勃発し、神聖ロー マ帝国を舞台として戦われた国際戦争のこと。ドイツが近代国家となることを妨げた)(1618-1648)で疲弊したドイツの復興のため力を尽くしましたが、晩年には王室の支援を失い、侯家の家史編纂という意に満たない仕事に携わりながら外国の学者や友人とひろく文通をかわすだけでした。
ニュートンとともに、微分積分学の創始者でもあります。
フランスの著名な思想家で百科全書の中心的人物であったディドロ(Diderot, Denis;1713-1784)は「この人はたった1人でプラトン、アリストテレス、アルキメデスの3人が一緒になってギリシャにもたらしたと同じぐらいの名声をドイツにもたらしたのである」と書いています。
結
今回は準同型定理(部分群の対応)の証明を解説しました。
準同型定理は、群論において最も重要と言っても過言ではないほどの定理です。
実際、群論の講義のゴールとして準同型定理を挙げていたりします。
今回は、\(G/{N}\)の部分群と、正規部分群\(N\)を含む部分群は一対一対応するという意味の準同型定理です。
次回は第二同型定理について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
代数についてより詳しく知りたい方は以下を参考にすると良いと思います!





コメントをする
定理1の証明の③の第一文目がわかりません。考えたこと:Hの任意の元はaNのように表現できると思う。n∈Nとするとπ(an)=anN=aNになると思う。nはNの任意の元なので、π^{-1}(H)はaNになる(ただし、aはHの元ごとに定まるいろいろな値で、それら全部を合わせたものがπ^{-1}(H))だと思う。どのようなaに対してもπ(aN)=aNN=aNより全体としてはHと一致する。この結論は最終的に③で示したいことと一致するものの、第一文の意味が分かりませんでした。教えていただけると幸いです
はっしー様
コメントありがとうごさいます!
お答えいたします。
①の前半は何をしているのか、というと\(\varphi\)がwell-definedであることを示しています。
具体的には、\(\mathbb{X}\)の要素に対して、\(\mathbb{Y}\)の要素がただ一つ定まるか?ということです。
すなわち、
\(H\in\mathbb{X}\)に対して、\(\varphi(H)\left( =\pi^{-1}(H)\right)\in\mathbb{Y}\)か?
を示そうとしています。
\(N\subset \pi^{-1}(H)\left( =\varphi(H)\right)\)を示します。
しかし、これは\(\pi(N)=1_{G/{N}}\)から分かります。
そして、\(1_{G/{N}}\in H\)です(\(H\)は\(G/{N}\)の部分群であるため)。
故に、\(\pi^{-1}\left( 1_{G/{N}}\right)\subset\pi^{-1}(H)\)
となります。
これが1行目の意味です。
いかがでしょうか?