本記事の内容
本記事は「なぜ正多面体は5つだけなのか?」と「正多面体群とは?」ということについて解説する生地です。
本記事を読むに当たり、特殊直交群について知っている必要があるため、以下の記事も合わせてご覧ください。
正多面体
群論編と銘打っておきながら、いきなり群論とは毛色が違うことを話します。
正多面体というものが初めて出現するのは(恐らく)中学数学だと思います。
御存知の通り、正多面体は世の中にたった5種類しか存在しません。
筆者が中学生のとき、「正多面体っていっぱいありそうなのに、本当に5種類だけなのかな?」と思ったのを覚えています。
最も、疑問に思ったのは一瞬で、大学に入学するまでその疑問を忘れて解決したことは有りませんでした(お恥ずかしい)。
正多面体とは何か?
恐らく「正多面体でしょ?知ってるよ」と思う方も多いと思いますが、正多面体とは何か?ということについて言及しておきます。
正多面体
正多面体とは、面が全て合同な正多角形で、頂点に集まる辺の数が全て等しい多面体のことである。余談(ユークリッド幾何学)
実は「面」やら「合同」やら「頂点」やらと言う話は本ブログではまだしていません。後の記事でユークリッド幾何学をしっかりやろうと思っています(筆者が学部生のときに1,2を争うほど面白かった内容です)。
その中で「点」やら「線」やらの話をしようと思います。
ちょっとだけネタバレをすると、「点」やら「線」やら「通る」などといった用語は幾何学的イメージを伴っていますが、いわるる”無定義用語”と呼ばれるものです。
以下が正多面体です。
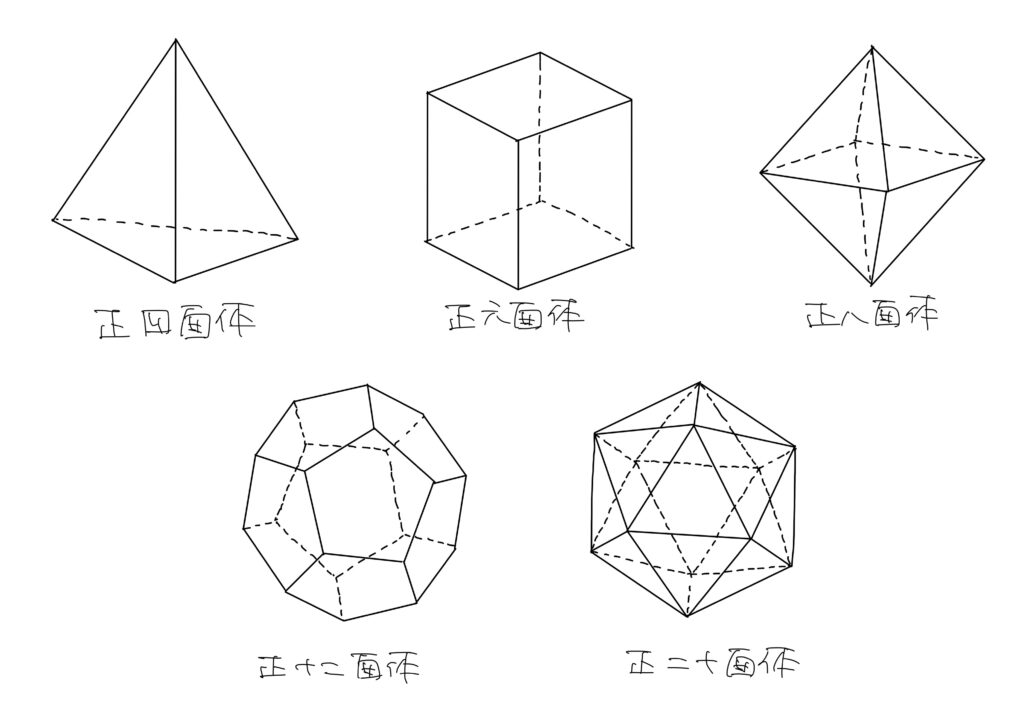
なぜ正多面体は5つだけなのか?
正多面体の面に注目してみると
| 正多面体の名前 | 面の図形 |
| 正四面体 | 正三角形 |
| 立方体(正六面体) | 正方形 |
| 正八面体 | 正三角形 |
| 正十二面体 | 正五角形 |
| 正二十面体 | 正三角形 |
です。
これを見ると、面の形は正三角形と正方形と正五角形しかありません。
正多角形自体は無限に存在するのに、立体となるとたった5種類しか存在しないというのが不思議でした。
どうして5種類しか存在しないのか、ということを証明します。
定理1.
正多面体は、正四面体、正六面体(立方体)、正八面体、正十二面体、正二十面体の5つのみである。定理1.の証明
正\(n\)角形の1つの各の角度は\(\displaystyle\frac{\pi(n-2)}{n}\)です。
1つの頂点に\(m\)個の面が集まっているとしましょう。
下の図は\(m=5\)、\(n=3\)の場合(正三角形が1つの頂点に5つ集まっている場合)に1つの頂点のまわりの面の展開図を考えたものです。
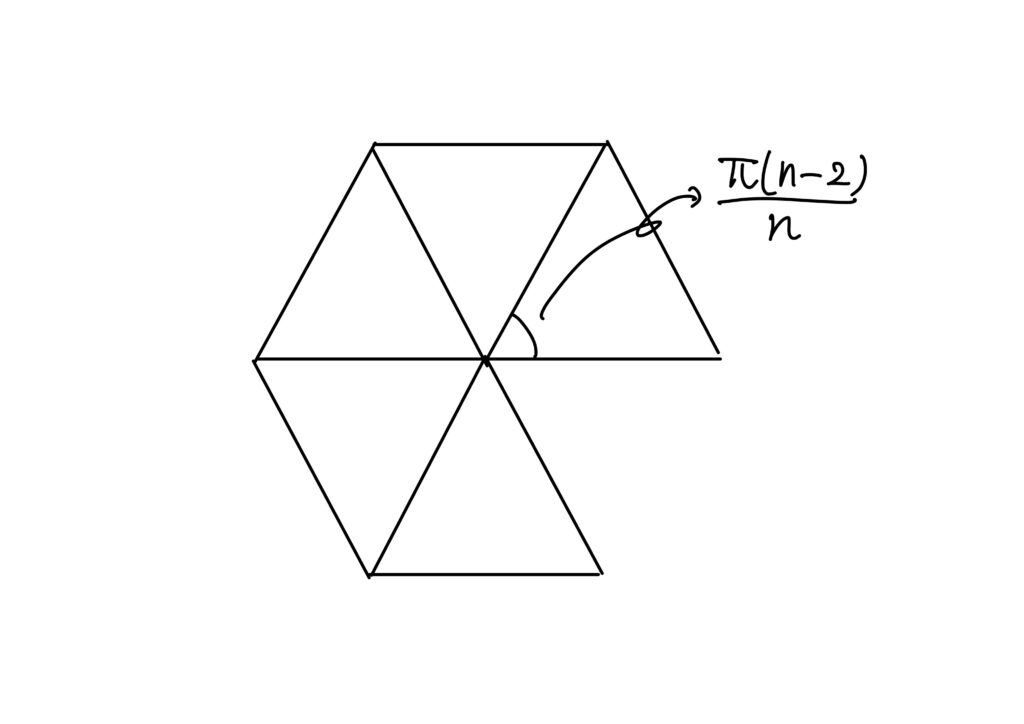
もし仮に、正\(n\)角形が頂点の周りを埋め尽くすと立体にはなりませんので、
$$
m\times\frac{\pi(n-2)}{n}<2\pi
$$
となります。
\(n=2\)の場合はそもそも図形になりえませんので、
$$
\frac{n-2}{n}\geq\frac{1}{3}
$$
です。
\(\displaystyle\frac{m(n-2)}{n}<2\)なので、\(m<6\)です。
故に、\(m=3,4,5\)となります。
\(m=3\)だったとすると、\(\displaystyle\frac{n-2}{n}<\frac{2}{3}\)、つまり\(n<6\)なので、\(n=3,4,5\)となります。
\(m=4\)のときは、\(\displaystyle\frac{n-2}{n}<\frac{1}{2}\)、つまり\(n<4\)なので、\(n=3\)です。
\(m=5\)であれば、\(\displaystyle\frac{n-2}{n}<\frac{2}{5}\)、つまり\(\displaystyle n<\frac{10}{3}\)なので、\(n=3\)です。
\(n,m\)が定まれば正多面体の形が決まります。
以上の議論から、\(n,m\)の可能性としては
$$
(n,m)=(3,3),\ (3,4),\ (3,5),\ (4,3),\ (5,3)
$$
です。
これらはそれぞれ正四面体、正八面体、正二十面体、正六面体(立方体)、正十二面体に対応しています。
定理1.の証明終わり
この証明を見ると、\(\pi\)といったある種高校数学で出現するものはありますが、証明自体は誠にシンプルです。
\(\pi\)についても\(\pi\)の部分を\(180^\circ\)と書けば中学生も理解できる証明の内容だと思います。
正多面体群
正多面体については極めて対称性が高いがゆえ、色々な性質を持ちます。
その1つが変換を考えることで群をなすことです。
正多面体群を一言で。
正多面体群を一言で表すと、
です。
ここで注意なのが、正多面体群の要素は正多面体ではないということです。
筆者だけかも知れませんが「正多面体群」という字面を見ると「正多面体自体が群になるのかな?」と思うかもしれません。
しかし違います。
あくまで正多面体をその同じ正多面体に写すような変換(写像)が要素です。
記号のお話
正多面体に記号を与えます。
| 正多面体の名前 | 記号 |
| 正四面体 | \(\mathcal{P}_4\) |
| 立方体(正六面体) | \(\mathcal{P}_6\) |
| 正八面体 | \(\mathcal{P}_8\) |
| 正十二面体 | \(\mathcal{P}_{12}\) |
| 正二十面体 | \(\mathcal{P}_{20}\) |
正多面体群の数学的な説明
ぱぱっと述べてしまいます。
正多面体群
正多面体\(\mathcal{P}_i\ (i=4,6,8,12,20)\)に対して、- 合同変換 \(\mathcal{P}_i\)を\(\mathbb{R}^3\)内の単位球面に内接させる。このとき原点を中心とする回転のうち、頂点を頂点に写すものを\(\mathcal{P}_i\)の合同変換という。
- 正多面体群 \(\mathcal{P}_i\)の合同変換\(\sigma\)の逆回転\(\sigma^{-1}\)もまた合同変換であり、合同変換\(\sigma,\tau\)を続けて行った変換(\(\tau\sigma\)と書く)もまた合同変換である。故に合同変換全体は、変換の合成(写像の合成)を演算として群をなす。この群を正\(i\)面体群という。また、正二面体群と合わせてこれらをまとめて正多面体群という。
要するに、正多面体を\(\mathbb{R}^3\)の原点がその中心となるようにしたとき、正多面体の頂点をその正多面体の別の頂点に写すような変換(原点を中心として回転させる写像)は、写像の合成でもって群をなすため、その群を正多面体群と呼びますよ、と言う話です。
ちょっとだけ踏み込んだ話
\(\mathbb{R}^3\)の原点がその中心と成る正多面体を考えます。
本題に入る前にちょこっと復習です。
特殊直交群の復習
でした。
\(G\)が\({\rm GL}_2(\mathbb{R})\)の部分群なら、包含写像\(G\longrightarrow {\rm GL}_2(\mathbb{R})\)は準同型です。
故に、\(G\)は\(\mathbb{R}^2\)に作用します。
特に、直交群\(O(2)\)について考えてみます。
ここで、直交群について少々説明します。
行列\(A\)に対して、その転置行列を\(A^\top\)と書きます。
行列\(A,B\)の積が定まるなら、\((AB)^\top=B^\top A^\top\)でした。
また、\(A\in{\rm GL}_n(\mathbb{R})\)なら、\((A^\top)^{-1}=\left( A^{-1}\right)^\top\)です。
\(G={\rm GL}_n(\mathbb{R})\)、
$$
H=\left\{g\in G\middle|g^\top g=I_n\right\}
$$
とします。
勿論、\(I_n\in H\)です。
\(g,h\in H\)なら、
$$
(gh)^\top(gh)=h^\top g^\top gh=h^\top(g^\top g)h=h^\top I_nh=h^\top h=I_n
$$
なので、\(gh\in H\)です。
また、\(g^\top=g^{-1}\)となるので、\(g g^\top=I_n\)です。
故に、
$$
(g^{-1})^\top g^{-1}=(g^\top)^{-1}g^{-1}=(gg^\top)^{-1}=I_n^{-1}=I_n
$$
となるので、\(g^{-1}\in H\)です。
従って、\(H\)は\(G\)の部分群です。
この\(H\)のことを直交群といいます。
直交群
$$ H=\left\{g\in G\middle|g^\top g=I_n\right\} $$ を\(O(n)\)と書き、直交群という。\(SO(n)=O(n)\cap {\rm SL}_n(\mathbb{R})\)とおき、特殊直交群という。詳しくは、【代数学の基礎シリーズ】群論編 その11を御覧ください。
特殊直交群の復習おしまい
さて、\({\rm SO}(3)\)の要素で正多面体を集合として不変にする要素全体は\({\rm SO}(3)\)の部分群です。
これらをそれぞれ、正四面体群、立方体群、正八面体群、正十二面体群、正二十面体群といいます。
正八面体の各辺の中点を結ぶと立方体になります。
また、正二十面体の各辺の中点を結ぶと正十二面体になります。
したがって、正八面体群と立方体群は同型で、正二十面体群と正十二面体群は同型です。
正四面体群、正八面体群、正二十面体群をそれぞれ\({\rm T},\ {\rm O},\ {\rm I}\)(tetrahedron、octahedron、icosahedronの頭文字)と書きます。
これらを正多面体群と呼ぶこともあります。
先に述べたとおり、正多面体はこれだけしか存在しませんが、代数幾何や整数論と古くから関係していますし、極めて高い対称性が興味深い性質を導きます。
皆様のコメントを下さい!
前回から背理法について少々語っています。
前回はゼノンの論法について紹介しました。
今回はゼノンの論法の具体例(実際にゼノンが言ったかは不明)を紹介します。
私の友人が透明人間になれる薬を作ることができると主張した。彼によれば透明になることによって自分の好きな場所に他人に気づかれずに行くことができるという。私は、そんなことは不可能だと言ったが彼は納得しない。そこで次のような理由を縷縷説明することになった。
「もし君が透明人間になれたとしよう。君が他人から見えないようにするには、体を構成する物質が、屈折を起こさないようなものでなければならない。さもなくば人が君のいる場所を見たとき、君の後ろにあるものとのズレが生じて、君がそこにいることが分かってしまうからだ。もちろん君の眼球も屈折が起らない物質でできていなければならない。そこで、”ものを見る”ということがどうして可能なのかを考えてみればわかるように、屈折がなければ君の眼球は機能せず、何も見ることはできない。すなわち君は盲目ということになる。盲目の君が好きな場所に他人に気づかれずに行くことがどうして可能なのか。」
「ちょっと冗談で言っただけなのに、そんなにムキになって論破しなくても…」とは思いましたが、こんなとこです。
数学において背理法が「鋭敏さ」を持つ論理であるのは、数学的言明(命題)が正しいか正しくな い(誤り)かの二者択一であることを仮定していることによります。
日常論理では多くの場合、正誤の境界は曖昧であり、したがって背理法が常に有効であるとは限りません。
実際、政治的論争や哲学的論議でよくあることですが、事の真偽が曖昧であると、ゼノンの論法は「詭弁」や「こじつけ」になりがちです。
ちなみに、詭弁を意味する英語 “sophistry”は、ギリシャ哲学の1つの学派である「知恵の実践者」(sophists)という言葉から派生しています。
今回はここまで。
感想など是非コメントで教えて下さい!
結
今回は、「正多面体がなぜ5種類しか存在しないのか?」「正多面体群とは何か?」ということについて解説しました。
正多面体が5種類しか存在しないのは展開図から考えることでシンプルに導けます。
正多面体群は、正多面体の頂点をその正多面体の頂点へ写す回転の変換から成る集合が群になることから、その群を正多面体群と呼ぶということでした。
次回は正多面体群の位数に着目します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。




コメントをする