「生成元と関係式で定義された群を使ってみよう！(例題)」【代数学の基礎シリーズ】群論編その31

本記事の内容
生成元と関係式で定義された群の軽い復習
例題1.
1. まずは問題
例題2.
1. 補足(なぜ $\mathcal{G}_3$ への全射準同型が存在したのか？)
皆様のコメントを下さい！
結

本記事の内容

本記事は、生成元と関係式で定義された群を例題とともに実際に使ってみる記事です。

本記事を読むに当たり、生成元と関係式で定義された群について知っている必要があるため、以下の記事も合わせて御覧ください。

生成元と関係式で定義された群の軽い復習

生成元と関係式で定義された群

$F_n/{N}$ を

$\left\langle x_1,\dots,x_n\middle| R_1(\boldsymbol{x})=1,\dots,R_m(\boldsymbol{x})=1\right\rangle$ と書き、生成元 $x_1,\dots,x_n$ と関係式 $R_1(\boldsymbol{x})=1,\dots,R_m(\boldsymbol{x})=1$ で定義された群という。

詳しくは、【代数学の基礎シリーズ】群論編その30を御覧ください。

今回は、生成元と関係式で定義された群を使って例題を解いてみましょう！
例題を解くことでよりイメージが付きやすいと思います。

例題1.

まずは問題

例題1.

$K　=\left\langle x,y\middle|x^3=y^2=1,\ yxy^{-1}=x^{-1}\right\rangle$ とすると、

$K\cong \mathcal{G}_3 \cong D_3$ であることを証明せよ。

解答

まず、 $\mathcal{G}_3$ を復習します。
$\mathcal{G}_3$ は対称群と呼ばれる群でした。
具体的には

$\displaystyle\mathcal{S}_X=\{f:X\longrightarrow X\mid f$ は全単射

$\}$

が写像の合成を演算として群となり、この群を対称群と呼んだのでした。

これは、まさに以前線型代数の記事で解説した置換が、写像の合成でもって群であるということです。
置換とは以下でした。

置換

$n\in\mathbb{N}$ とする。

$n$ 個の文字

$1,2,\dots,n$ からなる集合を

$M_n=\{1,2,\dots,n\}$ とする。写像

$\sigma:M_n\to M_n$ が全単射であるとき、

$\sigma$ を

$M_n$ の置換という。
　置換

$\sigma$ による対応が

$1\mapsto i_1,\ 2\mapsto i_2,\dots,n\mapsto i_n$ であるとする、すなわち、

$\sigma(1)=i_1,\ \sigma(2)=i_2,\dots,\ \sigma(n)=i_n$ とする。このとき

$\sigma$ を

$\sigma= \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix}$ と書く。

さて、 $G=\mathcal{G}_3$ 、 $\sigma=(1\ 2\ 3)$ 、 $\tau=(1\ 2)$ とします。
$G$ は $\sigma$ と $\tau$ で生成されます。

生成される部分群とは以下でした。

定理2.

$\langle S\rangle$ を

$S$ の要素による語全体の集合とするとき、次の1.、2.が成り立つ。

$\langle S\rangle$ は $G$ の部分群である。
$H$ が $G$ の部分群で $S$ を含むならば、 $\langle S\rangle\subset H$ である。すなわち、 $\langle S\rangle$ が $S$ を含むような最小の部分群である。

定理2.の証明は【代数学の基礎シリーズ】群論編その2を御覧ください。

ここで、前回証明した事実を使います。

定理3.

$G$ は

$n$ 個の生成元

$y_1,\dots,y_n$ を持ち、関係式

$R_1(y_1,\dots,y_n)=\dots=R_m(y_1,\dots,y_n)=1_G$ を持つとする。このとき、

$K=\left\langle x_1,\dots,x_n\middle|R_1(\boldsymbol{x})=1,\ \dots,R(\boldsymbol{x})=1\right\rangle$ から

$G$ への、

$\varphi(x_1)=y_1,\cdots,\varphi(x_n)=y_m$ を満たす全射準同型

$\varphi$ が存在する。

定理3.の証明は【代数学の基礎シリーズ】群論編その30を御覧ください。

ただし、次の事実を使いました。

命題4.

$A$ 、

$B$ が有限集合で、

$\left|A\right|=\left|B\right|$ であれば、次の1.、2.が成り立つ。

$A\subset B$ なら、 $A=B$ である。
写像 $f:A\longrightarrow B$ が単射であることと、全射であることは同値である。故に、このとき $f$ は全単射である。

命題4.の証明

(1.の証明)

(2.の証明)

$f$ が単射だとします。
このとき、 $\left|f(A)\right|=\left|A\right|=\left|B\right|$ です。
したがって、1.により $f(A)=B$ となり、 $f$ は全射です。
逆に $f$ が全射だとすると、任意の $b\in B$ に対して、 $a_b\in\ A$ 、 $f(a_b)=b$ となる要素 $a_b$ を選びます。
$b,b^\prime\in B$ 、 $b\neq b^\prime$ 、 $a_b=a_{b^\prime}$ ならば、 $b=f(a_b)=f(a_{b^\prime})=b^\prime$ となり矛盾です。
したがって、 $b\neq b^\prime$ ならば、 $a_b\neq a_{b^\prime}$ です。
よって、集合 $\left\{a_b\middle|b\in B\right\}\subset A$ の要素の個数は $\left|B\right|=\left|A\right|$ と等しいです。
したがって、1.により $\left\{a_b\middle|b\in B\right\}=A$ です。
これは、任意の $b\in B$ に対して $f^{-1}(b)$ が１つの要素により成ることを意味していて、 $f$ は単射です。

命題4.の証明終わり

戻ります。

$x^3=y^2=1$ なので、 $x^{-1}=x^2$ 、 $y^{-1}=y$ です。
よって、 $K$ の要素は $x,y$ のみ現れ、 $x^{-1},y^{-1}$ が現れない語で表されます。
$xy=yx^2$ なので、後のなかで $\cdots xy\cdots$ という部分があれば、 $xy$ を $yx^2$ で置き換えるということを繰り返し、 $y$ の左 $x$ が現れないようにすることができます。
したがって、 $K$ の要素は $y^ix^j$ という形に書くことができます。
$x^3=y^2=1$ なので、 $i=0,1$ 、 $j=0,1,2$ としてOKです。
したがって、 $\left|K\right|\leq6$ となり、 $\left|K\right|\cong\mathcal{G}_3$ です。

二面体群 $D_3$ も同じ生成元と関係式を持ち、 $\left|D_3\right|=6$ です。
したがって、全く同じ議論で $K\cong D_3$ であることもわかります。

例題1.の解答終わり

例題2.

例題2.

$G=\left\langle x,y\middle| x^4=y^3=1,\ xy=y^2x\right\rangle$ とするとき、

$\left|G\right|=12$ であることを証明せよ。また、

$G$ の全ての要素を

$x,y$ で表わせ。

解答

例題1.と同様な考察で、 $G$ の要素は $y^ix^j\ (i=0,1,2,\ j=-,1,2,3)$ という形で書けることがわかります。
故に、 $\left|G\right|=\leq 12$ です。
したがって、 $\left|G\right|\geq 12$ を示せばOKです。

$H_1=\mathcal{G}_3$ は $\sigma=(1\ 2)$ 、 $\tau=(1\ 2\ 3)$ で生成され、 $\sigma^4=\tau^3=1$ 、 $\sigma\tau=\tau^2\sigma$ となります。
また、 $H_2=\mathbb{Z}/{4\mathbb{Z}}$ 、 $\nu$ を $H_2$ の生成元、 $\rho=1$ ( $H_2$ の要素 $0+4\mathbb{Z}$ )とすれば、 $\nu^4=1$ 、 $\rho^3=1$ 、 $\nu\rho=\rho^2\nu$ です。
故に、全射準同型 $G\longrightarrow H_1,H_2$ が存在します(後述)。
$\left|H_1\right|=6$ 、 $\left|H_2\right|=4$ なので、 $\left|G\right|$ は $12$ で割り切れます。
したがって、 $\left|G\right|\geq12$ です。

例題2.の解答終わり

補足(なぜ $\mathcal{G}_3$ への全射準同型が存在したのか？)

$H=\left\langle x\right\rangle$ とすると、 $\left|G/{H}\right|=3$ となるはずなので、 $G$ の $G/{H}$ への左作用により定まる置換表現があるからです。
$G/{H}$ の大表現として $\left\{1,y,y^2\right\}$ が取れるので、 $y$ は $(1\ 2\ 3)$ として作用するはずです。
$xH=H$ 、 $xyH=y^2H$ 、 $xy^2H=yH$ なので、 $x$ は(2\ 3)\)として作用するはずです。
先の解答では同じことなので $(1\ 2)$ としました。

ちなみに、 $G$ を $\mathcal{G}_{12}$ の部分群として明示的に実現することも可能です。
$z_i=x^{i-1},\quad z_{4+i}=yx^{i-1},\quad z_{8+i}=y^2x^{i-1}\quad(i=1,2,3,4)$
とすると、 $G=\left\{z_1,\cdots,z_{12}\right\}$ であり、 $\left|G\right|=12$ となるはずなので、 $z_1,\dots,z_{12}$ は全て異なるはずです。
そこで $G$ の左からの席により $G$ から $\mathcal{G}_{12}$ への準同型が得られるはずです。
$yz_1=z_5,\dots,yz_{12}=z_4$ となり、同様に $x$ の作用も考えると、 $x,y$ は
$\sigma=(1\ 2\ 3\ 4)(5\ 10\ 7\ 12)(6\ 11\ 8\ 9),\quad \tau=(1\ 5\ 9)(2\ 6\ 10)(3\ 7\ 11)(4\ 8\ 12)$
として作用するはずです。
$\sigma^4=\tau^3=1$ 、 $\sigma\tau\sigma^{-1}=\tau^2$ であることが以下の事実から従います。

補題5.

$(i_1\ \cdots\ i_l)\in\mathcal{G}_n$ を巡回置換、

$\sigma\in\mathcal{G}_n$ とすると、

$\sigma(i_1\ \cdots\ i_l)\sigma^{-1}=\left(\sigma(i_1)\ \cdots\ \sigma(i_l) \right)$ である。

補題5.の証明は【代数学の基礎シリーズ】群論編その19を御覧ください。

したがって、定理3.から全射準同型 $G\longrightarrow \left\langle \sigma,\tau\right\rangle$ が存在します。

$\sigma,\tau$ の位数はそれぞれ $4,3$ なので、 $\left|\left\langle\sigma,\tau \right\rangle\right|$ は $4,3$ で割り切れます。
したがって、 $\left|G\right|$ も $4,3$ で割り切れ、 $\left|G\right|\geq12$ です。
$\left|G\right|\leq12$ なので、 $\left|G\right|=12$ であり、また $z_1,\dots,z_{12}$ はすべて異なり、 $G$ が $\left\langle \sigma,\tau\right\rangle$ と同型であることがわかります。
これで $G$ を $\mathcal{G}_{12}$ の部分群として実現できました。

皆様のコメントを下さい！

前回は、ピタゴラス学派の幾何学が危機に陥ったという話で、それを救ったのがユードクソスだ、という話をしました。
今回はその続きです。

ユードクソスが定めた比の相等
4つの線分

$\alpha_1,\beta_1,\alpha_2,\beta_2$ について

$\alpha_1:\beta_1=\alpha_2=\beta_2$ であることは次が成り立つことである。

$m\alpha_1> n\beta_1$ ならば、必ず $m\alpha_2> n\beta_2$
$m\alpha_1= n\beta_1$ ならば、必ず $m\alpha_2= n\beta_2$
$m\alpha_1< n\beta_1$ ならば、必ず $m\alpha_2< n\beta_2$

ここで

$m,n$ は自然数とする。

ちなみに、ユークリッドは『原論』で

ユークリッドの『原論』の引用
「比とは、同種の2つの量の間の大きさに関するある種の関係である」
「第１の量と第３の量の同数倍が第２の量と第４の量の同数倍に対して、何倍されようと、同順にとられたとき、それぞれ共に大きいか、共に等しいか、または共に小さい時、第１の量は第２の量に対して第３の量が第４の量に対すると同じ比にあるといわれる」

ここで、第１の量 $=\alpha_1$ 、第２の量 $=\beta_1$ 、第３の量 $=\alpha_2$ 、第４の量 $=\beta_2$ です。

実は、比は大小関係もあります。
「同数倍された量のうち、第１の倍量が第２の倍量より大きいが、第３の倍量が第４の倍量より大きくないとき、第１の量は第２の量に対して第３の量が第４の量に対するより、大きい火を持つといわれる」

これを言い換えれば、

$\alpha_2:\beta_2<\alpha_1:\beta_1\Longleftrightarrow n\beta_1< m\alpha_2\leq n\beta_2$ となる自然数

$m,n$ が存在

です。
もし実数と線分の長さの比の値が実数で表されることを「知っているなら」 $\displaystyle x_1=\frac{\alpha_1}{\beta_1}$ 、 $\displaystyle x_2=\frac{\alpha_2}{\beta_2}$ とすると、相等と大小は次のように表されます。

相等
２つの性の実数

$x_1,x_2$ に対して、

$x_1=x_2$ であるのは

$\begin{cases} \displaystyle\frac{n}{m}<x_1\Longrightarrow \frac{n}{m}< x_2\\ \displaystyle\frac{n}{m}=x_1\Longrightarrow \frac{n}{m}=x_2\\ \displaystyle\frac{n}{m}>x_1\Longrightarrow \frac{n}{m}> x_2\\ \end{cases}$ が成り立つことである。

大小
２つの性の実数

$x_1,x_2$ に対して、

$x_1<x_2$ であるのは、

$\displaystyle x_2\leq\frac{n}{m}< x_1$ となる有理数

$\displaystyle\frac{m}{n}$ が存在することである。が成り立つことである。

そして「実数を知っていると」上記のことが正しいことがわかります。
実際、大小に関する主張は、実数の集合の中で有理数の集合の稠密性から導かれます。
この意味は任意の区間 $(x_2,x_1)$ には無限個の有理数が存在することです。
相等に関する主張は、 $x_2<x_1$ とするとき、 $\displaystyle x_2\leq\frac{n}{m}<x_1$ となる有理数 $\displaystyle\frac{n}{m}$ が存在するから、 $\displaystyle x_1<\frac{n}{m}$ にも関わらず $x_2\geq x_1$ となって矛盾です。

幾何学の話に戻ります。
一般の場合は次が成り立ちます。

定理.

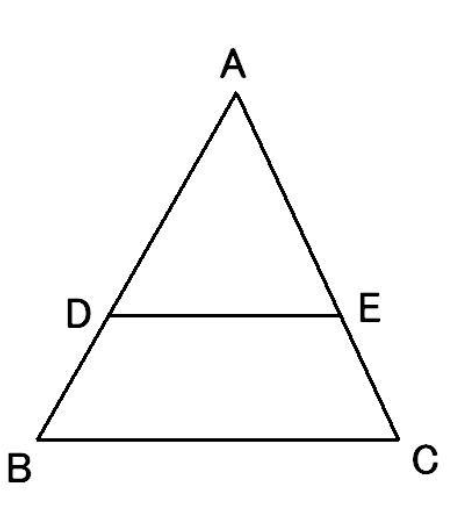
$\triangle ABC$ の辺

$AB$ の上の点

$D$ から辺

$BC$ に平行な直線を引き、辺

$AC$ との交点を

$E$ とする。このとき、

$AD:DB=AE:EC$ である。

証明

以前のように、 $AD=\alpha_1$ 、 $DB=\beta_1$ 、 $AE=\alpha_2$ 、 $EC=\beta_2$ とします。
$m\alpha_1=n\beta_1$ のときはすでに $m\alpha_2=n\beta_2$ であることを示しました。

$m\alpha_1>n\beta_1$ とします。
辺 $AB$ を $m+n$ 等分して、 $A$ から $k$ 番目の等分点を $B_k$ とすると、
$\begin{eqnarray} (m+n)AB_n&=&nAB=n(\alpha_1+\beta_1)=n\alpha_1+m\beta_1\\ &<&n\alpha_1+m\alpha_1=(m+n)\alpha_1=(m+n)AD \end{eqnarray}$
です。
故に、 $AB<AD$ となって、 $B_n$ は辺 $AD$ 上にあります。
前と同様に $C_n$ を考えれば、 $C_n$ は辺 $AE$ 上にあります。
故に $m\alpha_2>n\beta_2$ です。

$m\alpha_1<n\beta_1$ の場合も同様にして $m\alpha_2<n\beta_2$ です。

証明終わり

次回はユードクソスの「無限」の取り扱い方です。

ユードクソスは以前紹介しましたが、天才ですね。
ユードクソスの他の業績についてご存知の方は是非コメントで教えて下さい！

結

今回は、生成元と関係式で定義された群を例題とともに実際に使ってみました。
特に、例題2.については今後の位数12の群を観察する上での試金石となる例題です。
群論(というより代数)は実際に手を動かして解いてみる、ということがしにくい分野だと思います。
ぜひ実際に手を動かして解いてほしいです。

次回から数回に渡って位数12の群について解説します。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34