本記事の内容
本記事はヘッセ行列の符号によって極値が判定できるという定理を明示、証明する記事です。
本記事を読むにあたり実対称行列の符号と行列式の性質について知っている必要があるため、以下の記事も合わせてご覧ください。
↓実対称行列の符号の記事
↓行列式の記事
本記事で言いたいことと前回の軽い復習
本記事では次の定理を証明することが目標です。
定理0.(ヘッセ行列の符号による極値の判定)
\(\Omega\)が\(\mathbb{R}^n\)の開集合、\(f:\Omega\to\mathbb{R}\)が\(C^2\)級、\(\boldsymbol{a}\in\Omega\)、\(f^\prime(\boldsymbol{a})=\boldsymbol{0}\)、\(H(a)\)は\(f\)の\(\boldsymbol{a}\)におけるヘッセ行列とする。このとき、以下の3つが成り立つ。- \(H(\boldsymbol{a})\)が正値\(\Rightarrow f\)は\(\boldsymbol{a}\)で狭義の極小となる。
- \(H(\boldsymbol{a})\)が負値\(\Rightarrow f\)は\(\boldsymbol{a}\)で狭義の極大となる。
- \(H(\boldsymbol{a})\)が不定符号\(\Rightarrow f\)は\(\boldsymbol{a}\)で極値を取らない。
ここで、極値とは以下でした。
\(A\subset\mathbb{R}^n\)、\(f:A\to\mathbb{R}\)、\(\boldsymbol{a}\in A\)とする。
- 極大 \(f\)が\(a\)で極大とは $$ (\exists \varepsilon>0)\ {\rm s.t.}\ f(\boldsymbol{a})=\max_{\boldsymbol{x}\in A\cap B(\boldsymbol{a};\varepsilon)}f(\boldsymbol{x})=\max_{\substack{\boldsymbol{x}\in A \\ \|\boldsymbol{x}-\boldsymbol{a}\|<\varepsilon}}f(\boldsymbol{x}) $$ が成り立つことをいう。また、\(f\)が\(\boldsymbol{a}\)で狭義の極大とは、 $$ (\exists \varepsilon>0)\ {\rm s.t.}\ \left[(\forall \boldsymbol{x}\in A:0<\|\boldsymbol{x}-\boldsymbol{a}\|<\varepsilon)\Rightarrow f(\boldsymbol{a})>f(\boldsymbol{x})\right] $$ が成り立つことをいう。
- 極小 \(f\)が\(a\)で極小とは $$ (\exists \varepsilon>0)\ {\rm s.t.}\ f(\boldsymbol{a})=\min_{\boldsymbol{x}\in A\cap B(\boldsymbol{a};\varepsilon)}f(\boldsymbol{x})=\min_{\substack{\boldsymbol{x}\in A \\ \|\boldsymbol{x}-\boldsymbol{a}\|<\varepsilon}}f(\boldsymbol{x}) $$ が成り立つことをいう。また、\(f\)が\(\boldsymbol{a}\)で狭義の極小とは、 $$ (\exists \varepsilon>0)\ {\rm s.t.}\ \left[(\forall \boldsymbol{x}\in A:0<\|\boldsymbol{x}-\boldsymbol{a}\|<\varepsilon)\Rightarrow f(\boldsymbol{a})<f(\boldsymbol{x})\right] $$ が成り立つことをいう。
また、ヘッセ行列とは以下でした。
ヘッセ行列(Hesse行列、ヘシアン)
\(C^2\)級の関数\(f\)に対して、 $$ H(\boldsymbol{x})=\left( \frac{\partial^2 f}{\partial x_i\partial x_j}(\boldsymbol{x})\right) $$ とおき、これを\(f\)の\(\boldsymbol{x}\)におけるヘッセ行列(Hesse行列、ヘシアン)と呼ぶ。さらに、正値、負値、不定符号とは以下でした。
実対称行列の正値性、負値性、不定符号
\(A=\left( a_{ij}\right)\)を\((n,n)\)型の実対称行列とする。このとき- \(A\)が正値であるとは、\(A\)の固有値が全て正であるときをいう。
- \(A\)が負値であるとは、\(A\)の固有値が全て負であるときをいう。
- \(A\)が不定符号であるとは、\(A\)の固有値に正のもの、負のものがあるときをいう。
さて、多変数のテイラーの定理により、\(f^\prime(\boldsymbol{a})\boldsymbol{h}=\boldsymbol{0}\)のとき、
\begin{eqnarray}
f(\boldsymbol{a}+\boldsymbol{h})
&=&f(\boldsymbol{a})+\frac{1}{2}\left( H(\boldsymbol{\boldsymbol{a}+\theta\boldsymbol{h}})\boldsymbol{h},\boldsymbol{h}\right)\\
\end{eqnarray}
と書けるのでした。
ということは、\(\left( H(\boldsymbol{a}+\theta\boldsymbol{h}),\boldsymbol{h}\right)\)の符号によって\(f(\boldsymbol{a})\)と\(f(\boldsymbol{a}+\boldsymbol{h})\)の大小関係が分かるので、ヘッセ行列の符号を知りたい、という話でした。
実対称行列の符号の判定方法
※薄々お気づきかと思いますが、本記事は7割が線型代数のお話です(笑)。
実対称行列の符号は結局の所固有値の符号でした。
ということは、実対称行列\(A\)の固有方程式\(\varphi_A(t)=0\)の解の符号を調べることで\(A\)の符号が分かります。
しかしながら、固有方程式は解くのが大変な場合が多いです。
3次の固有方程式の時点で既に難しいです。
実は、小行列式の行列式によって、\(A\)の正値性、負値性を判定できるという事実があります。
それを説明するために、首座行列という行列を定めます。
首座行列
なんてことありません。
行列の左上から\((k,k)\)型の行列を引っこ抜いた、その引っこ抜いた行列を\(k\)次首座行列といいます。
\(k\)次首座行列
正方行列\(A\)を $$ A= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{n1}&a_{m2}&\cdots &a_{nn}\\ \end{pmatrix} $$ と書いたとする。このとき、\(k=1,\dots,n\)に対して $$ A_k= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1k}\\ a_{21}&a_{22}&\cdots &a_{2k}\\ \vdots&\vdots& \ddots&\vdots\\ a_{k1}&a_{m2}&\cdots &a_{kk}\\ \end{pmatrix} $$ を\(A\)の\(k\)次首座行列という。例えば、こんなのです。
例1. \(\displaystyle A=
\begin{pmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{pmatrix}
\)としたとき、
$$
A_1=1,\quad
A_2=
\begin{pmatrix}
1&2\\
4&5\\
\end{pmatrix},\quad
A_3=A=
\begin{pmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{pmatrix}
$$
です。
次に、二次形式の標準形について話します。
二次形式の標準形
二次形式\(\boldsymbol{x}^\top A\boldsymbol{x}\)に対して、\(A\)は対称行列なので、適切な直交行列\(P\)でもって対角化できます。
そこで、m\(\boldsymbol{x}=P\boldsymbol{y}\)とすると、
\begin{eqnarray}
\boldsymbol{x}^\top A\boldsymbol{x}&=&\left(\boldsymbol{y}^\top P^\top\right)AP\boldsymbol{y}\\
&=&\alpha_1y_1^2+\alpha_2y_2^2+\dots+\alpha_ny_n^2
\end{eqnarray}
となります。
ただし、\(\alpha_1,\alpha_2,\dots,\alpha_n\)は\(A\)の重複を含めた固有値です。
さらに、これらを並び替えて
\begin{eqnarray}
&&\alpha_1,\alpha_2,\dots,\alpha_p>0,\\
&&\alpha_{p+1},\alpha_{p+2},\dots,\alpha_{p+q}<0,\\
&&\alpha_{p+q+1},\alpha_{p+q+2},\dots,\alpha_n=0
\end{eqnarray}
とします。
ちなみに、\(p+q\)は\(A\)のランクです。
さらに、変数を以下のように変換してみます。
\begin{eqnarray}
&&y_i=\frac{1}{\sqrt{\alpha_i}}z_i\quad(1\leq i\leq p)\\
&&y_j=\frac{1}{\sqrt{-\alpha_j}}z_j\quad(p+1\leq j\leq p+q)
\end{eqnarray}
このとき、
$$
\boldsymbol{x}^\top A\boldsymbol{x}=z_1^2+z_2^2+\dots+z_p^2-z_{p+1}^2-\dots-z_{p+q}^2
$$
となります。
これを二次形式\(\boldsymbol{x}^\top A\boldsymbol{x}\)の標準形と呼びます。
首座行列の行列式の符号で正値性、負値性を判定できます。
では、主張を明示して証明します。
定理2.(首座小行列式の符号による正値性、負値性の判定)
\(n\)次実対称行列\(A=\left( a_{ij}\right)\)に対して、\(A_k\)を\(A\)の\(k\)次首座行列とするとき、以下の1.および2.が成り立つ。- \(A\)が正値\(\ \Longleftrightarrow\ \left(\forall k\in\{1,\dots,n\}\right)\ \det\left(A_k \right)>0\)。
- \(A\)が負値\(\ \Longleftrightarrow\ \left(\forall k\in\{1,\dots,n\}\right)\ (-1)^k\det\left(A_k \right)>0\)(すなわち、\(\det\left( A_1\right),\det\left( A_2\right),\dots,\det\left( A_n\right)\)の符号が交互に負、正、負、正、…)
定理2.の証明
(1.の証明)
1-①(\(\Rightarrow\))の証明
\(A\)が正値だとします。
\(k\in\{1,\dots,n\}\)、\(\boldsymbol{x}\in\mathbb{R}^k\)とするとき、\(\boldsymbol{x}^\prime=(x,0,\dots,0)\in\mathbb{R}^n\ \)(\(0\)が\(n-k\)個並んでいる)とすると、
$$
\left( A_k\boldsymbol{x},\boldsymbol{x}\right)=\left( A\boldsymbol{x}^\prime,\boldsymbol{x}^\prime\right)
$$
です。
\(\boldsymbol{x}\neq\boldsymbol{0}\)とすると、\(\boldsymbol{x}^\prime\neq\boldsymbol{0}\)ですから、\(A\)が正値であることから、
$$
\left( A_k\boldsymbol{x},\boldsymbol{x}\right)=\left( A\boldsymbol{x}^\prime,\boldsymbol{x}^\prime\right)>0
$$
です。
ただし、次の事実を使いました。
定理3.(実対称行列の符号と2次形式の符号)
\(A=\left( a_{ij}\right)\)が\(n\)次実対称行列とするとき、次の1.、2.、3.が成り立つ。- \(A\)が正値\(\ \Longleftrightarrow\ \forall \boldsymbol{h}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}\)に対して、\(\left( A\boldsymbol{h},\boldsymbol{h}\right)>0\)。
- \(A\)が負値\(\ \Longleftrightarrow\ \forall \boldsymbol{h}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}\)に対して、\(\left( A\boldsymbol{h},\boldsymbol{h}\right)<0\)。
- \(A\)が不定符号\(\ \Longrightarrow\ (\exists \boldsymbol{h},\boldsymbol{h}^\prime\in\mathbb{R}^n)\ {\rm s.t.}\ \left(A\boldsymbol{h},\boldsymbol{h} \right)>0,\ \left(A\boldsymbol{h},\boldsymbol{h} \right)<0\)。
定理3.の証明は【解析学の基礎シリーズ】偏微分編 その8を御覧ください。
さて、\(\left( A\boldsymbol{x}^\prime,\boldsymbol{x}^\prime\right)>0\)なのですから、\(A_k\)もまた正値です。
ということは、\(A_k\)の固有値を\(\lambda_j^{(k)}\ (j=1,\dots,k)\)と書いたときに、\(\lambda_j^{(k)}>0\)ですから、
$$
\det\left( A_k\right)=\prod_{j=1}^k\lambda_j^{(k)}>0
$$
です。
ちなみに、なぜ、\(\displaystyle \det\left( A_k\right)=\prod_{j=1}^k\lambda_j^{(k)}\)と書けるか、ということですが、以下の3つが成り立っているからです。
定理4.
\(n\)次実正方行列\(A\)に対して、次の2つの条件は同値である。- \(A\)は対称行列である。
- \(A\)は適当な直交行列\(P\)によって対角化できる。 すなわち、 $$ P^{-1}AP= \begin{pmatrix} \lambda_1&&\huge{O}\\ &\ddots&\\ \huge{O}&&\lambda_n \end{pmatrix} $$ である。
定理4.の証明は【線型代数学の基礎シリーズ】固有値編 その4を御覧ください。
定理5.
\(n\)次正方行列\(A\)および\(B\)が相似であれば、 $$ \varphi_A(t)=\varphi_B(t) $$ である。従って、\(A\)と\(B\)の固有値全体は重複を込めて一致する。定理5.の証明は【線型代数学の基礎シリーズ】固有値編 その1を御覧ください。
命題6.
\(n\)次上三角行列\(A\)の行列式\(\det(A)\)は\(A\)の対角成分の積に等しい。すなわち、次が成り立つ。 $$ \det(A)=a_{11}a_{22}\dots a_{nn} $$命題6.の証明は【線型代数学の基礎シリーズ】行列式編 その2を御覧ください。
1-②(\(\Leftarrow\))の証明
「任意の\(n\)次実対称行列\(A\)に対して、\(\det\left( A_k\right)>0\ (k=1,\dots,n)\)ならば、\(A\)は正値である」ことを\(n\)に関する数学的帰納法で証明します。
\(n=1\)のとき、\(A_1=a_{11}\)について、\(\det\left(A_1 \right)=a_{11}\)ですから、\(\det\left( A_1\right)>0\)であれば、\(a_{11}>0\)で、かつ\(A_1\)の固有値は\(a_{11}\)そのものですから、\(A_1\)は正値です。
\(n-1\)のときに成り立つとします。
\(A\)は\(n\)次実対称行列で、\(\det\left( A_k\right)>0\ (k=1,\dots,n)\)を満たすとして、\(A_{n-1}\)は正値です。
ここで、\(A\)を以下のようにブロック分けします。
$$
A=
\begin{pmatrix}
A_{n-1}&\boldsymbol{b}\\
\boldsymbol{b}^\top&c
\end{pmatrix}
$$
ただし、\(\boldsymbol{b}\)は\((n-1,1)\)型のベクトルです。
ここで、\(A_{n-1}\)は正値なので、先程示したことから\(\det\left( A_{n-1}\right)>0\)により\(\det\left( A_{n-1}\right)\neq0\)なので、\(A_{n-1}\)には逆行列\(A_{n-1}^{-1}\)が存在することに注意して、
$$
P=
\begin{pmatrix}
I_{n-1}&A_{n-1}^{-1}\boldsymbol{b}\\
\boldsymbol{0}^\top&1
\end{pmatrix},\quad
B=
\begin{pmatrix}
A_{n-1}&\boldsymbol{0}\\
\boldsymbol{0}^\top&c-\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b}
\end{pmatrix},\quad
$$
とします。
ただし、\(I_{n-1}\)は\(n-1\)次の単位行列です。
このとき、
$$
P^\top BP=A
$$
です。
実際、
\begin{eqnarray}
P^\top BP&=&
\begin{pmatrix}
I_{n-1}&\boldsymbol{0}\\
\left(A_{n-1}^{-1}\boldsymbol{b}\right)^\top&1
\end{pmatrix}
\begin{pmatrix}
A_{n-1}&\boldsymbol{0}\\
\boldsymbol{0}^\top&c-\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b}
\end{pmatrix}
\begin{pmatrix}
I_{n-1}&A_{n-1}^{-1}\boldsymbol{b}\\
\boldsymbol{0}^\top&1
\end{pmatrix}\\
&=&
\begin{pmatrix}
I_{n-1}&\boldsymbol{0}\\
\boldsymbol{b}^\top A_{n-1}^{-1}&1
\end{pmatrix}
\begin{pmatrix}
A_{n-1}&\boldsymbol{0}\\
\boldsymbol{0}^\top&c-\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b}
\end{pmatrix}
\begin{pmatrix}
I_{n-1}&A_{n-1}^{-1}\boldsymbol{b}\\
\boldsymbol{0}^\top&1
\end{pmatrix}\\
&=&
\begin{pmatrix}
A_{n-1}&\boldsymbol{0}\\
\boldsymbol{b}^\top&c-\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b}
\end{pmatrix}
\begin{pmatrix}
I_{n-1}&A_{n-1}^{-1}\boldsymbol{b}\\
\boldsymbol{0}^\top&1
\end{pmatrix}\\
&=&
\begin{pmatrix}
A_{n-1}&\boldsymbol{b}\\
\boldsymbol{b}^\top&\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b}+c-\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b}
\end{pmatrix}\\
&=&
\begin{pmatrix}
A_{n-1}&\boldsymbol{b}\\
\boldsymbol{b}^\top&c
\end{pmatrix}=A
\end{eqnarray}
です。
ここで、1つ補題を考えます。
補題7.(シルベスタの慣性法則)
二次形式の標準形は一意的に定まる。すなわち、変数にどんな線型変換を施して標準形に写しても、正負の項の数\(p,q\)は一定である。補題7.の証明
2通りの変数変換
$$
\boldsymbol{x}=P\boldsymbol{y},\quad \boldsymbol{x}=Q\boldsymbol{z}
$$
によって、二通りの標準形
\begin{eqnarray}
\boldsymbol{x}^\top A\boldsymbol{x}&=&y_1^2+y_2^2+\dots+y_p^2-y_{p+1}^2-\dots-y_{p+q}^2\\
&=&z_1^2+z_2^2+\dots+z_s^2-z_{s+1}^2-\dots-z_{s+t}^2
\end{eqnarray}
を得たとしましょう。
このとき、\(p+q=s+t={\rm rank}(A)\)です。
\(p>s\)だとして矛盾を導きます(背理法!)。
\(x_1,x_2,\dots,x_n\)に関する斉次一次方程式系
\begin{eqnarray}
&&y_i=0\quad(i=p+1,p+2,\dots,n)\\
&&z_j=0\quad (j=1,2,\dots,s)
\end{eqnarray}
は自明でない解\(a_1,a_2,\dots,a_n\)を持ちます。
実際、方程式の個数は\(n-p+s\)であり、変数の数\(n\)よりも小さいからです。
$$
P^{-1}
\left(
\begin{array}{c}
a_1\\
a_2\\
\vdots\\
\vdots\\
\vdots\\
\vdots\\
a_n
\end{array}
\right)
=\left(
\begin{array}{c}
b_1\\
b_2\\
\vdots\\
b_p\\
0\\
\vdots\\
0
\end{array}
\right),\quad
Q^{-1}
\left(
\begin{array}{c}
a_1\\
a_2\\
\vdots\\
\vdots\\
\vdots\\
\vdots\\
a_n
\end{array}
\right)
=\left(
\begin{array}{c}
0\\
\vdots\\
0\\
c_{s+1}\\
\vdots\\
\vdots\\
c_n
\end{array}
\right)
$$
の形をしているので、
$$
b_1^2+b_2^2+\dots+b_p^2=-c_{s+1}^2-c_{s+2}^2-\dots-c_n^2
$$
です。
従って、\(b_1=b_2=\dots=b_p=0\)となって、\(a_1,a_2,\dots,a_n\)が自明でない解であることに矛盾します。
従って、\(p=s\)でなければなりません。
補題7.の証明終わり
では、定理2.の証明に戻ります。
今、
$$
P^\top BP=A
$$
となって、補題7.から\(P^\top BP\)の正値性、負値性と\(A\)の正値性、負値性は一致しているので、\(P^\top BP=A\)の正値性をしょうめいできれば良いことになります。
ここでもう一個補題を与えます。
補題8.
対称行列の逆行列もまた対称行列である。すなわち、 $$ A^\top,\quad \det\left(A \right)\neq0\quad \Longleftrightarrow\quad \left( A^{-1}\right)^\top=A^{-1} $$ である。補題8.の証明
\(A\)が対称かつ正則だとしましょう。
このとき、\(AA^{-1}=A^{-1}A=I\)の転置を取れば、\(\left( A^{-1}\right)^\top A^\top=A^\top\left( A^{-1}\right)^\top=I\)です。
\(A\)が対称であることから、\(\left( A^{-1}\right)^\top A=A\left( A^{-1}\right)^\top=I\)です。
すなわち、\(\left( A^{-1}\right)^\top=A^{-1}\)です。
補題8.の証明終わり
では、定理2.の証明に戻ります。
今、\(\det\left( P\right)=1\)であることに注意すると、補題8.から
$$
\det\left( A\right)=\det\left(A_{n-1}\right)\cdot\left( c-\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b}\right)
$$
です。
\(\det\left( A\right)>0\)、\(\det\left( A_{n-1}\right)>0\)により、\(c-\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b}>0\)です。
\(\boldsymbol{x}=(x_1,\dots,x_n)^\top\in\mathbb{R}^n\)に対して、\(\boldsymbol{x}^\prime=(x_1,\dots,x_n)^\top\)とすると、
$$
\left( B\boldsymbol{x},\boldsymbol{x}\right)=\left( A_{n-1}\boldsymbol{x}^\prime,\boldsymbol{x}^\prime\right)+\left(c-\boldsymbol{b}^\top A_{n-1}^{-1}\boldsymbol{b} \right)x_n^2
$$
です。
\(\boldsymbol{x}\neq\boldsymbol{0}\)により、\(\boldsymbol{x}^\prime\neq\boldsymbol{0}\)または\(x_n\neq0\)であることに注意すると、\(\left( B\boldsymbol{x},\boldsymbol{x}\right)>0\)です。
従って定理3.から\(B\)は正値です。
(2.の証明)
\(A\)が負値である、ということは\(-A\)が正値、ということですので、上記の証明の\(A\)を\(-A\)に置き換えて全く同じ議論で証明することができます。
従って、ここでは省略します。
定理2.の証明終わり
実際に首座行列の行列式の符号で正値性、負値性を判定してみます。
例9. \(\displaystyle A=
\begin{pmatrix}
2&1&1\\
1&2&1\\
1&1&2
\end{pmatrix}\)の正値性、負値性を判定してみます。
まずは真正直に固有値を計算してみると、固有値は\(4,1,1\)と分かりますので、\(A\)は正値です。
しかし、3次の正方行列ですので、計算は面倒くさいです。
そこで、首座行列の行列式を計算してみます。
\begin{eqnarray}
\det\left( A_1\right)&=&2>0,\\
\det\left( A_2\right)&=&
\det\begin{pmatrix}
2&1\\
1&2
\end{pmatrix}=2\cdot2-1\cdot1=3>0,\\
\det\left( A_3\right)&=&
\det\begin{pmatrix}
2&1&1\\
1&2&1\\
1&1&2
\end{pmatrix}=2\cdot2\cdot2+1\cdot1\cdot1+1\cdot1\cdot1-1\cdot2\cdot1-2\cdot1\cdot1-2\cdot1\cdot1\\
&=&8+1+1-2-2-2=4>0
\end{eqnarray}
により、\(A\)が正値であることが分かります。
「え?結局面倒くさくない?」と思うかもしれません。
確かに、そもそも行列式の計算が面倒くさいというのもありますが、固有方程式の解を求めるには行列式を計算して更に因数分解して解を求めます。
つまり、首座行列の行列式を求めるというアプローチは多次方程式を解く、という操作の分だけ楽ちんということです。
ヘッセ行列の符号による極値判定定理の証明
ようやっと本題に入っていきます。
何を示したいか、というと以下でした。
定理0.(ヘッセ行列の符号による極値の判定)(再掲)
\(\Omega\)が\(\mathbb{R}^n\)の開集合、\(f:\Omega\to\mathbb{R}\)が\(C^2\)級、\(\boldsymbol{a}\in\Omega\)、\(f^\prime(\boldsymbol{a})=\boldsymbol{0}\)、\(H(a)\)は\(f\)の\(\boldsymbol{a}\)におけるヘッセ行列とする。このとき、以下の3つが成り立つ。- \(H(\boldsymbol{a})\)が正値\(\Rightarrow f\)は\(\boldsymbol{a}\)で狭義の極小となる。
- \(H(\boldsymbol{a})\)が負値\(\Rightarrow f\)は\(\boldsymbol{a}\)で狭義の極大となる。
- \(H(\boldsymbol{a})\)が不定符号\(\Rightarrow f\)は\(\boldsymbol{a}\)で極値を取らない。
では、証明に入っていきます。
今までは線型代数のお話でしたが、以降は解析のお話が主になってきます。
定理0.の証明
\(\Omega\)が開集合なので、
$$
(\exists \varepsilon>0)\ {\rm s.t.}\ B(\boldsymbol{a};\varepsilon)\subset\Omega
$$
を満たしています。
ここで、多変数のテイラーの定理を使います。
定理10.(多変数のテイラーの定理)
\(n,k\in\mathbb{N}\)、\(\Omega\)を\(\mathbb{R}^n\)の開集合、\(f:\Omega\to\mathbb{R}\)を\(C^k\)の関数、\(\boldsymbol{a}\in\Omega\)、\(\boldsymbol{h}\in\mathbb{R}^n\)、線分\([\boldsymbol{a},\boldsymbol{a}+\boldsymbol{h}]\subset\Omega\)とするとき、次の式を満たすような\(0<\theta<1\)が存在する。 $$ f(\boldsymbol{a}+\boldsymbol{h})=\sum_{m=0}^{k-1}\frac{1}{m!}\left(d^mf \right)_\boldsymbol{a}(\boldsymbol{h})+\frac{1}{k!}\left( d^kf\right)_{\boldsymbol{a}+\theta\boldsymbol{h}}(\boldsymbol{h}). $$ ただし、\(\left( d^mf\right)_\boldsymbol{x}(\boldsymbol{h})\)は\(f\)の\(\boldsymbol{x}\)における\(m\)次微分と呼ばれる\(\boldsymbol{h}\)についての\(m\)次形式で、次の式で定められる。 $$ \left( d^mf\right)_\boldsymbol{x}(\boldsymbol{h})=\sum_{1\leq i_1,i_2,\cdots,i_m\leq n}\frac{\partial^mf}{\partial x_{i_1}\partial x_{i_2}\cdots\partial x_{i_m}}(x)h_{i_1}h_{i_2}\cdots h_{i_m}. $$定理10.(多変数のテイラーの定理)の証明は【解析学の基礎シリーズ】偏微分編 その8を御覧ください。
定理10.から、
\begin{eqnarray}
(\forall \boldsymbol{h}\in\mathbb{R}^2:\|\boldsymbol{h}\|<\varepsilon)\ (\exists \theta\in(0,1))\ {\rm s.t.}\ f(\boldsymbol{a}+\boldsymbol{h})&=&f(\boldsymbol{a})+f^\prime(\boldsymbol{a})\boldsymbol{h}+\frac{1}{2}\left( H(\boldsymbol{a}+\theta\boldsymbol{h})\boldsymbol{h},\boldsymbol{h}\right)\\
&=&f(\boldsymbol{a})+\frac{1}{2}\left( H(\boldsymbol{a}+\theta\boldsymbol{h})\boldsymbol{h},\boldsymbol{h}\right)
\end{eqnarray}
です。
(1.の証明)
\(H(\boldsymbol{a})\)が正値であれば、定理2.から
$$
(\forall k\in\{1,\dots,n\})\ \det\left( H_k(\boldsymbol{a})\right)>0
$$
です。
また、\(f\)は\(C^2\)級ですので、\(\det\left( H(\boldsymbol{x})\right)\)は連続だから、
$$
(\exists \varepsilon^\prime\in(0,\varepsilon))\ {\rm s.t.}\ \left( \forall \boldsymbol{h}\in\mathbb{R}^n:\|\boldsymbol{h}\|<\varepsilon^\prime\right)\ (\forall \theta\in(0,1))\ \det\left( H_k(\boldsymbol{a}+\theta\boldsymbol{h})\right)>0
$$
です。
今、\(\det\left( H_k(\boldsymbol{a}+\theta\boldsymbol{h})\right)>0\)ということが分かったので、再度定理2.から\(H(\boldsymbol{a}+\theta\boldsymbol{h})\)は正値です。
故に、\(\boldsymbol{h}\neq\boldsymbol{0}\)なのであれば、定理3.から\(\left( H(\boldsymbol{a}+\theta\boldsymbol{h}\boldsymbol{h},\boldsymbol{h})\right)>0\)です。
従って、\(f(\boldsymbol{a}+\boldsymbol{h})>f(\boldsymbol{a})\)となって、\(f\)は\(\boldsymbol{a}\)で狭義の極小です。
(2.の証明)
1.の証明において、\(\det\left( H_k(\boldsymbol{a})\right)>0\)の部分を\(\det\left( H_k(\boldsymbol{a})\right)<0\)と書き換えればよいので、省略します。
(3.の証明)
\(H(\boldsymbol{a})\)が不定符号だとしましょう。
このとき、\(H(\boldsymbol{a})\)の固有値の中に正のものと負のものが存在しています。
それをそれぞれ\(\lambda,\mu\)としましょう。
すなわち、
です。
このとき、\(\lambda,\mu\)のそれぞれに属する固有ベクトルを\(\boldsymbol{u},\boldsymbol{v}\)と書けば、
$$
H(\boldsymbol{a})\boldsymbol{u}=\lambda\boldsymbol{u},\quad H(\boldsymbol{a})\boldsymbol{v}=\mu\boldsymbol{v}\quad(\boldsymbol{u},\boldsymbol{v}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\})
$$
を満たしています。
ここで、上記の\(\boldsymbol{u}\)および\(\boldsymbol{v}\)は
$$
0<\|\boldsymbol{u}\|<\varepsilon,\quad 0<\|\boldsymbol{v}\|<\varepsilon
$$
を満たしているように取ることができます。
なぜならば、固有ベクトルは実数倍しても固有ベクトルだからです。
さて、
$$
g(t)=f(\boldsymbol{a}+t\boldsymbol{u}),\quad h(t)=f(\boldsymbol{a}+t\boldsymbol{v})
$$
とすると、
\begin{eqnarray}
g^\prime(t)&=&f^\prime(\boldsymbol{a}+t\boldsymbol{u})\boldsymbol{u},\quad g^{\prime\prime}(t)=\left( H(\boldsymbol{a}+t\boldsymbol{u},\boldsymbol{u})\right),\\
h^\prime(t)&=&f^\prime(\boldsymbol{a}+t\boldsymbol{v})\boldsymbol{v},\quad h^{\prime\prime}(t)=\left( H(\boldsymbol{a}+t\boldsymbol{v},\boldsymbol{v})\right),\\
g^\prime(0)&=&f^\prime(\boldsymbol{a})\boldsymbol{u},\quad g^{\prime\prime}(0)=\left( H(\boldsymbol{a},\boldsymbol{u})\right)=\lambda(\boldsymbol{u}, \boldsymbol{u})=\lambda\|\boldsymbol{u}\|^2>0,\\
h^\prime(0)&=&f^\prime(\boldsymbol{a})\boldsymbol{v},\quad h^{\prime\prime}(0)=\left( H(\boldsymbol{a},\boldsymbol{v})\right)=\mu(\boldsymbol{v}, \boldsymbol{v})=\mu\|\boldsymbol{v}\|^2<0,\\
\end{eqnarray}
となります。
\(g(t)\ (|t|<1)\)は\(t=0\)で狭義の極小、\(h(t)\ (|t|<1)\)は\(t=0\)で狭義の極大です。
従って、変化する方向によって極小となったり極大となったりするので、\(f\)は\(\boldsymbol{a}\)で極値を取りません。
定理0.の証明終わり
実際に極値を計算して求めてみましょう!
では一緒に極値を計算して求めてみましょう。
例11. \(f(x,y)=x^3+y^3-3xy\)の極値を求めてみます。
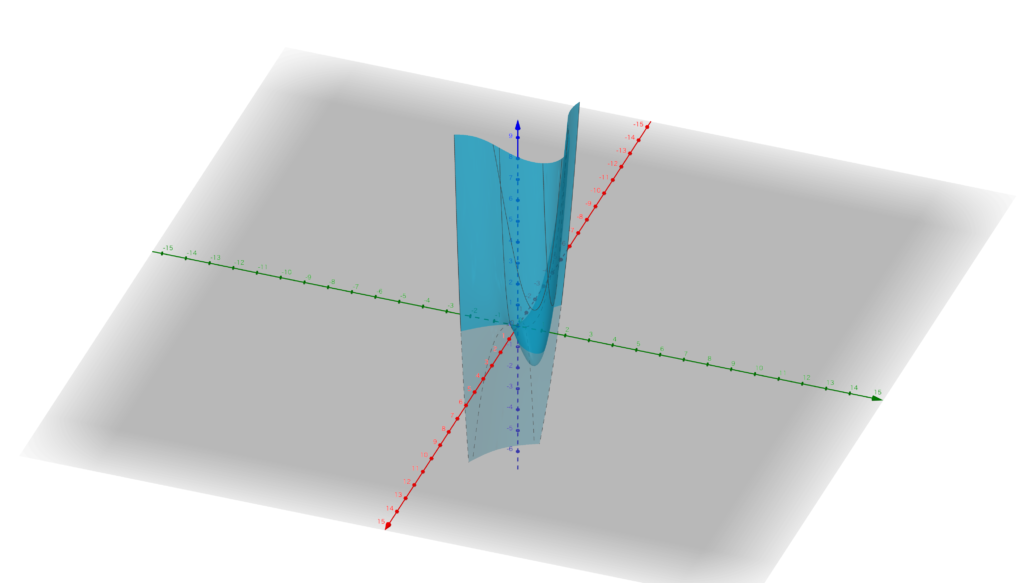
まずは導関数を計算します。
$$
f^\prime(\boldsymbol{x})=\nabla f(\boldsymbol{x})=
\left(
\begin{array}{c}
\displaystyle\frac{\partial f}{\partial x}\\
\displaystyle\frac{\partial f}{\partial y}
\end{array}
\right)=
\left(
\begin{array}{c}
3x^2-y\\
3y^2-x
\end{array}
\right)
$$
です。
また、\(f\)のヘッセ行列\(H\)は
$$
H=
\begin{pmatrix}
\displaystyle\frac{\partial^2 f}{\partial x^2}&\displaystyle\frac{\partial^2 f}{\partial x\partial y}\\
\displaystyle\frac{\partial^2 f}{\partial y\partial x}&\displaystyle\frac{\partial^2 f}{\partial y^2}
\end{pmatrix}
=
\begin{pmatrix}
6x&-3\\
-3&6y
\end{pmatrix}
$$
です。
さて、\(f^\prime(\boldsymbol{a})=\nabla f(\boldsymbol{a})=\boldsymbol{0}\)となる点\(\boldsymbol{a}\)を求めてみましょう。
\begin{eqnarray}
\nabla f(x,y)=0&\Longleftrightarrow&
\begin{cases}
3x^2-3y=0\\
3y^2-3x=0
\end{cases}\\
&\Longleftrightarrow&
\begin{cases}
x^2-y=0\\
y^2-x=0
\end{cases}\\
&\Longleftrightarrow&
\begin{cases}
y=x^2\\
x^4-x=0
\end{cases}\\
&\Longleftrightarrow&
x=y=0\lor x=y=1
\end{eqnarray}
つまり、\((x,y)=(0,0)\)と\((x,y)=(1,1)\)で\(f\)は極値を取りうる、ということです。
従って、\(H(0,0)\)と\(H(1,1)\)の正値性、負値性を確認します。
- \(H(0,0)\)について
$$
H(0,0)=\begin{pmatrix}
6\times 0&-3\\
-3&6\times0
\end{pmatrix}=
\begin{pmatrix}
0&-3\\
-3&0
\end{pmatrix}
$$
です。
従って、\(\det\left( H(0,0)_1\right)=0\)となって正値でも負値でもないため、\(H(0,0)\)は不定符号だから、\((x,y)=(0,0)\)では極値を取りません。 - \(H(1,1)\)について
$$
H(1,1)=\begin{pmatrix}
6\times 1&-3\\
-3&6\times1
\end{pmatrix}=
\begin{pmatrix}
6&-3\\
-3&6
\end{pmatrix}
$$
です。
従って、
\begin{eqnarray}
\det\left(H(1,1)_1\right)&=&6>0,\\
\det\left(H(1,1)_2\right)&=&6\times6-(-3)\times(-3)=27>0
\end{eqnarray}
となります。
故に、\(H(1,1)\)は正値ですので、この点\((x,y)=(1,1)\)で\(f\)は極小を取ります。
また具体的な極小値は
$$
f(1,1)=1^3+1^3-3\times1\times1=-1
$$
です。
以上のことから、\(f\)は\((x,y)=(1,1)\)で極小値\(-1\)を取る、ということが分かります。
読者の皆様のコメントを下さい!
筆者が初めてヘッセ行列による極値判定を学んだとき、「すげえ。行列の正値性、負値性で極値をとりうる定義域の要素の候補が分かるんだあ。」と割と感動しました。
同時に線型代数は解析的な問題を特にあたっての一つの道具的な存在(というと良い気がしない方がいらっしゃるかと思いますが…)でもあるのだなあ。と思いました。
線型代数はなんとも表情豊かでありとあらゆるところでさも当然のように使われます。
さて、余談でしたが、今回読者の皆様にお聞きしたいのが、「どんな定理に感動しましたか?」ということです。
巷ではやれ「オイラーの公式が美しいんだ!」みたいな話をよく聞きます。
確かに「そうだね。きれいだよね。」と思いますが、みんな言ってるのでありがたみが薄れてきている気がします(個人的な話)。
そこで、皆様にいままで出会った定理で「こりゃ凄い!」と思った定理をコメントで教えて下さい!
筆者の場合、1つにしぼるのは難しいですが、オイラーの多面体定理が好きです。
結
今回は、ヘッセ行列の正値性、負値性によって極値判定が可能だ、ということについて証明を与えました。
多次元の場合、極値はいっぱいありますし、そもそも図を描くことすら困難です。
そんな中、ヘッセ行列という行列の符号を観察することで、どこで極値をとるか、ということが分かるという強力な事実です。
それを理解するには、実は線型代数の知識が必要です。
一見解析のお話と思いきや、実は線型代数の手法をフル稼働します。
線型代数が至るところで扱われるという良い例でもあると思います。
次回は、解析学の中でも随一の大事さを誇る逆関数定理のイントロを解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!





コメントをする