「ヘッセ行列による極値判定①〜ヘッセ行列？実対称行列の正値性？負値性？不定符号？〜」【解析学の基礎シリーズ】偏微分編その9

本記事の内容
こんな問題を考えたいのです。
内点 $\boldsymbol{a}$ で極値を取れば $f^\prime(\boldsymbol{a})=\boldsymbol{0}$ です。
1. 極値って何ですか？
2. 全微分可能な関数が内点で極値を取れば、全微分係数は $0$ です。
ヘッセ行列の符号によって極値かどうかを判定できる場合があります。
1. ヘッセ行列？
2. で、ヘッセ行列って何ですか？
今回と次回のメインとなる定理(証明は次回行います)
1. 今回と次回のメインとなる定理(ヘッセ行列の符号による極値の判定)
実対称行列の正値性、負値性、不定符号
なぜヘッセ行列の符号が極大極小と関係があるんですか？
余談(読者の皆様のコメントを下さい！)
結

本記事の内容

本記事はヘッセ行列、実対称行列の正値性、負値性について解説する記事です。

本記事を読むにあたり、全微分と多変数のテイラーの定理を知っている必要があるため、以下の記事も合わせて御覧ください。

↓全微分の記事

↓多変数のテイラーの定理の記事

こんな問題を考えたいのです。

まずは、どんな問題を考えたいのか、ということを述べます。

$K$ を $\mathbb{R}^2$ 内の3点 $O=(0,0)$ 、 $A=(1,0)$ 、 $B=(0,1)$ 、 $C=(1,1)$ を頂点とする正方形とします。
すなわち、
$K=\{(x,y)\in\mathbb{R}^2| 0\leq x\leq1,\ 0\leq y\leq1\}$
とします。
また、
$f(x,y)=3x^2+2y^2+2xy-2x-2y+1$
で定めるとき、 $f$ の最大値と最小値を求なさい、という問題を考えたいのです。
これはあくまで簡単な例ですので、もっと $K$ が複雑なのもあります。

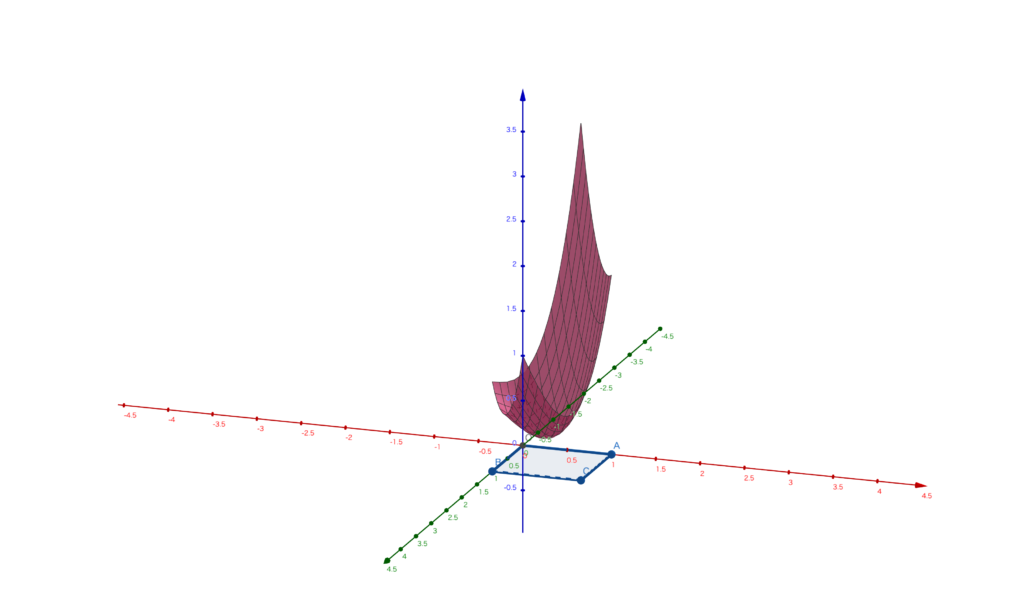
勿論、上記の図を描ければ「ここで最大値をとって、ここで最小値を取るなあ」と分からんでもないわけですが、描くのは誠に難しいと思います。

さて、「どうしようか？」という話ですが、高校数学でやった方針に則ってみましょう。
そこで、まずは全微分してみます。
$f^\prime(x,y)=\left( \frac{\partial f}{\partial x}\ \frac{\partial f}{\partial y}\right)=(6x+2y-2\ 4y+2x^2)$
ここで、 $f^\prime(x,y)=\boldsymbol{0}$ としてみます。
すると、
$f^\prime(x,y)=\boldsymbol{0}\Leftrightarrow (x,y)=\left( \frac{1}{5},\frac{2}{5}\right)$
が導けます。

さてさて、ここからどうしたら良いでしょうか。
１変数関数の場合のように増減表は書けません。
そもそも１変数の場合は $f^\prime$ の符号を調べましたが、２変数の場合 $f^\prime$ はベクトルですので、「ベクトルの符号を調べるってどういうこと？」となるわけです。

しかしながら、実はすぐ後で証明するのですが、

$f$ が定義域内の内点

$\boldsymbol{a}$ で極大(もしくは極小)をとるならば、

$f^\prime(\boldsymbol{a})=\boldsymbol{0}$ である。

は多変数関数についても成り立つのです。

加えて、

$f^\prime(\boldsymbol{a})=\boldsymbol{0}$ 、

$\boldsymbol{a}$ の十分近くで

$f^{\prime\prime}>0$ ならば、

$f$ は

$\boldsymbol{a}$ で極小値をとる。

という主張は多変数関数へ拡張することができます。

では次に「極値とはなんぞや？」ということを説明します。

内点 $\boldsymbol{a}$ で極値を取れば $f^\prime(\boldsymbol{a})=\boldsymbol{0}$ です。

なにはともあれ、まずは「極値って何？」というところから説明します。

極値って何ですか？

極値とは以下です。

$A\subset\mathbb{R}^n$ 、

$f:A\to\mathbb{R}$ 、

$\boldsymbol{a}\in A$ とする。

極大

$f$

$a$

極大

$(\exists \varepsilon>0)\ {\rm s.t.}\ f(\boldsymbol{a})=\max_{\boldsymbol{x}\in A\cap B(\boldsymbol{a};\varepsilon)}f(\boldsymbol{x})=\max_{\substack{\boldsymbol{x}\in A \\ \|\boldsymbol{x}-\boldsymbol{a}\|<\varepsilon}}f(\boldsymbol{x})$

$f$

$\boldsymbol{a}$

狭義の極大

$(\exists \varepsilon>0)\ {\rm s.t.}\ \left[(\forall \boldsymbol{x}\in A:0<\|\boldsymbol{x}-\boldsymbol{a}\|<\varepsilon)\Rightarrow f(\boldsymbol{a})>f(\boldsymbol{x})\right]$

極小

$f$

$a$

極小

$(\exists \varepsilon>0)\ {\rm s.t.}\ f(\boldsymbol{a})=\min_{\boldsymbol{x}\in A\cap B(\boldsymbol{a};\varepsilon)}f(\boldsymbol{x})=\min_{\substack{\boldsymbol{x}\in A \\ \|\boldsymbol{x}-\boldsymbol{a}\|<\varepsilon}}f(\boldsymbol{x})$

$f$

$\boldsymbol{a}$

狭義の極小

$(\exists \varepsilon>0)\ {\rm s.t.}\ \left[(\forall \boldsymbol{x}\in A:0<\|\boldsymbol{x}-\boldsymbol{a}\|<\varepsilon)\Rightarrow f(\boldsymbol{a})<f(\boldsymbol{x})\right]$

極大、極小を総称して極値と呼んだり、極大、極小をそれぞれ単に極値と呼ぶこともある。

「なんか小難しいことを言ってるなあ」と思うかもしれませんが、なんてことありません。
平たく言うと、

ある定義域内の点

$\boldsymbol{a}$ の

$f$ の値

$f(\boldsymbol{a})$ が、

$\boldsymbol{a}$ の近くの範囲での最大値であれば、

$f(\boldsymbol{a})$ を極大といって、

$\boldsymbol{a}$ の近くで最小値であれば極小という。

ということです。
高校でやった三次関数を例に取ると、以下です。

全微分可能な関数が内点で極値を取れば、全微分係数は $0$ です。

さて、主張を明示します。

定理1.(全微分可能な関数が内点で極値を取れば、全微分係数は $0$ である。)

$\Omega$ が

$\mathbb{R}^n$ の開集合、

$f:\Omega\to\mathbb{R}$ は全微分可能で、

$\boldsymbol{a}\in\Omega$ 、

$f$ は

$\boldsymbol{a}$ で極大(または極小)ならば、

$f^\prime(\boldsymbol{a})=\boldsymbol{0}$ (これは

$\nabla f(\boldsymbol{a})=\boldsymbol{0}$ とも書ける)である。

証明はなんてことありません。

定理1.の証明

$\Omega$ が開集合なので、
$(\exists r>0)\ {\rm s.t.}\ B(\boldsymbol{a};r)\subset \Omega$
が成り立っています( $\Omega$ が開集合であるとはこれを満たすことでした！)。

さて、 $f$ が $\boldsymbol{x}=\boldsymbol{a}$ で極大をとるとき、各 $i\in\{1,\dots,n\}$ に対して、
$\varphi_i:(a_i-r,a_i+r)\ni x_i\mapsto f(a_1,\dots,a_{i-1},x_i,\dots,a_{i+1},\dots,a_n)\in\mathbb{R}$
という写像を考えると、 $f$ が $\boldsymbol{a}$ で極大をとるのだから、 $\varphi_i$ は $x_i=a_i$ で極大値を取ります。
従って、
$0=\varphi^\prime_i(a_i)=\frac{\partial f}{\partial x_i}(\boldsymbol{a})=0$
となります。
これが任意の $i$ について成り立つわけですので、
$f^\prime(\boldsymbol{a})=\left( \frac{\partial f}{\partial x_1}(\boldsymbol{a})\ \cdots \ \frac{\partial f}{\partial x_n}(\boldsymbol{a})\right)=(0\ \cdots\ 0)=\boldsymbol{0}$
が成り立ちます。

定理1.の証明終わり

ここで注意を一つ。
それは「定理1.の逆は成り立ちません。」ということです。
すなわち、たとえ $f^\prime(\boldsymbol{a})=\boldsymbol{0}$ だったとしても、 $f$ が $\boldsymbol{a}$ で極値を取らないことがある、ということです。

実際、 $f(x)=x^3$ 、 $a=0$ としたとき、 $f^\prime(a)=f^\prime(0)=0$ ですが $f$ は $a=0$ で極大でも極小でもありません。

ヘッセ行列の符号によって極値かどうかを判定できる場合があります。

まずは「ヘッセ行列って何？」というところから話をします。

ヘッセ行列？

「ヘッセ行列はこれです！」と最初から言い切っても良いのですが、どういう背景でヘッセ行列なるものが出現したのか、ということから話したほうが良いと思いますので、そこから話します。

多変数のテイラーの定理を使います。

多変数のテイラーの定理は何だったかというと、以下でした。

定理2.(多変数のテイラーの定理)

$n,k\in\mathbb{N}$ 、

$\Omega$ を

$\mathbb{R}^n$ の開集合、

$f:\Omega\to\mathbb{R}$ を

$C^k$ の関数、

$\boldsymbol{a}\in\Omega$ 、

$\boldsymbol{h}\in\mathbb{R}^n$ 、線分

$[\boldsymbol{a},\boldsymbol{a}+\boldsymbol{h}]\subset\Omega$ とするとき、次の式を満たすような

$0<\theta<1$ が存在する。

$f(\boldsymbol{a}+\boldsymbol{h})=\sum_{m=0}^{k-1}\frac{1}{m!}\left(d^mf \right)_\boldsymbol{a}(\boldsymbol{h})+\frac{1}{k!}\left( d^kf\right)_{\boldsymbol{a}+\theta\boldsymbol{h}}(\boldsymbol{h}).$ ただし、

$\left( d^mf\right)_\boldsymbol{x}(\boldsymbol{h})$ は

$f$ の

$\boldsymbol{x}$ における

$m$ 次微分と呼ばれる

$\boldsymbol{h}$ についての

$m$ 次形式で、次の式で定められる。

$\left( d^mf\right)_\boldsymbol{x}(\boldsymbol{h})=\sum_{1\leq i_1,i_2,\cdots,i_m\leq n}\frac{\partial^mf}{\partial x_{i_1}\partial x_{i_2}\cdots\partial x_{i_m}}(x)h_{i_1}h_{i_2}\cdots h_{i_m}.$

定理2.(多変数のテイラーの定理)の証明は【解析学の基礎シリーズ】偏微分編その8を御覧ください。

この定理2.において、 $k=2$ の場合を用います。
$f$ が $C^2$ 級であれば、任意の(十分小さい) $h\neq0$ に対して、
$\begin{eqnarray} f(\boldsymbol{a}+\boldsymbol{h})&=&f(\boldsymbol{a})+\left( d^2f\right)_\boldsymbol{a}(\boldsymbol{h})+\frac{1}{2!}\left( d^2f\right)_{\boldsymbol{a}+\theta\boldsymbol{h}}(\boldsymbol{h})\\ &=&f(\boldsymbol{a})+f^\prime(\boldsymbol{a})\boldsymbol{h}+\frac{1}{2}\sum_{i,j=1}^n\frac{\partial^2 f}{\partial x_i\partial x_j}(\boldsymbol{a}+\theta\boldsymbol{h})h_ih_j \end{eqnarray}$
となります。

$f^\prime(\boldsymbol{a})=\boldsymbol{0}$ とすると、 $f^\prime(\boldsymbol{a})\boldsymbol{h}=\boldsymbol{0}$ なので、
$f(\boldsymbol{a}+\boldsymbol{h})=f(\boldsymbol{a})+\frac{1}{2}\sum_{i,j=1}^n\frac{\partial^2 f}{\partial x_i\partial x_j}(\boldsymbol{a}+\theta\boldsymbol{h})h_ih_j$
が成り立っています。

$\|\boldsymbol{h}\|$ が”小さい”ときには、右辺第2項は”おおよそ” $\boldsymbol{h}$ の2次形式なので、符号が一定になる場合があります。

$\displaystyle(\exists \varepsilon>0)\ {\rm s.t.}\ (\forall \boldsymbol{h}:0<\|\boldsymbol{h}\|<\varepsilon)\quad \sum_{i,j=1}^n\frac{\partial^2 f}{\partial x_i\partial x_j}(\boldsymbol{a}+\theta\boldsymbol{h})h_ih_j>0\ \Longrightarrow f$ は

$\boldsymbol{a}$ で極小。

$\boldsymbol{a}$ で極大。

これはあくまでサラッと述べたに過ぎないので、厳密ではありません。
勿論、以下で厳密な話をします。

で、ヘッセ行列って何ですか？

ではヘッセ行列というものを定めます。

ヘッセ行列(Hesse行列、ヘシアン)

$C^2$ 級の関数

$f$ に対して、

$H(\boldsymbol{x})=\left( \frac{\partial^2 f}{\partial x_i\partial x_j}(\boldsymbol{x})\right)$ とおき、これを

$f$ の

$\boldsymbol{x}$ におけるヘッセ行列(Hesse行列、ヘシアン)と呼ぶ。

ここで、以下の定理を思い出しましょう。

定理3.

$\Omega$ は

$\mathbb{R}^n$ の開集合、

$\boldsymbol{f}:\Omega\to\mathbb{R}^m$ は

$C^2$ 級とするとき、任意の

$i,j\in\{1,\dots,n\}$ および

$\boldsymbol{a}\in\Omega$ に対して、

$\frac{\partial^2 \boldsymbol{f}}{\partial x_i\partial x_j }(\boldsymbol{a})=\frac{\partial^2 \boldsymbol{f}}{\partial x_j\partial x_i }(\boldsymbol{a})$

定理3.の証明は【解析学の基礎シリーズ】偏微分編その2を御覧ください。

さて、今、ヘッセ行列の $f$ は $C^2$ 級なので、定理3.から
$\frac{\partial^2 \boldsymbol{f}}{\partial x_i\partial x_j }(\boldsymbol{a})=\frac{\partial^2 \boldsymbol{f}}{\partial x_j\partial x_i }(\boldsymbol{a})$
です。
ということは、ヘッセ行列は実対称行列、すなわち成分が実数でかつ自身と転置行列が一致しているっ行列となります。

これを使えば、
$\begin{eqnarray} f(\boldsymbol{a}+\boldsymbol{h})&=&f(\boldsymbol{a})+f^\prime(\boldsymbol{a})\boldsymbol{h}+\frac{1}{2}\sum_{i,j=1}^n\frac{\partial^2 f}{\partial x_i\partial x_j}(\boldsymbol{a}+\theta\boldsymbol{h})h_ih_j\\ &=&f(\boldsymbol{a})+f^\prime(\boldsymbol{a})\boldsymbol{h}+\frac{1}{2}\left( H(\boldsymbol{\boldsymbol{a}+\theta\boldsymbol{h}})\boldsymbol{h},\boldsymbol{h}\right)\\ &=&f(\boldsymbol{a})+\frac{1}{2}\left( H(\boldsymbol{\boldsymbol{a}+\theta\boldsymbol{h}})\boldsymbol{h},\boldsymbol{h}\right)\\ \end{eqnarray}$
と書き換えることができます。

一番のポイントとしては、
$\left( d^2f\right)_\boldsymbol{x}(\boldsymbol{h})=\left(H(\boldsymbol{x}),\boldsymbol{h} \right)$
であることです。

今回と次回のメインとなる定理(証明は次回行います)

さて、ヘッセ行列の符号によって極値を判定できる場合がある、というのが今回と次回のメインとなる定理です。

「ちょっと待って。ヘッセ行列って行列だよね。行列の符号って何？」となるかと思います。
それは後で説明します。
まずは「ヘッセ行列の符号」というモノが分かれば、関数の極値が半手できる場合がありますよ、という事実を先に述べておきます(証明は次回行います)。

今回と次回のメインとなる定理(ヘッセ行列の符号による極値の判定)

定理0.(ヘッセ行列の符号による極値の判定)

$\Omega$ が

$\mathbb{R}^n$ の開集合、

$f:\Omega\to\mathbb{R}$ が

$C^2$ 級、

$\boldsymbol{a}\in\Omega$ 、

$f^\prime(\boldsymbol{a})=\boldsymbol{0}$ 、

$H(a)$ は

$f$ の

$\boldsymbol{a}$ におけるヘッセ行列とする。このとき、以下の3つが成り立つ。

$H(\boldsymbol{a})$ が正値 $\Rightarrow f$ は $\boldsymbol{a}$ で狭義の極小となる。
$H(\boldsymbol{a})$ が負値 $\Rightarrow f$ は $\boldsymbol{a}$ で狭義の極大となる。
$H(\boldsymbol{a})$ が不定符号 $\Rightarrow f$ は $\boldsymbol{a}$ で極値を取らない。

実は、後で述べますが、行列は正値でも負値でも不定符号でもない場合もあります(次節で述べます)。
この場合は定理0.が適用できないため、別のアプローチかもっと詳しく調べなければ極値か否かは判定できません。

さて、定理0.を見れば明快かと思いますが、要するに、ある点 $\boldsymbol{a}$ でのヘッセ行列が正値か負値か不定符号かが分かれば、点 $\boldsymbol{a}$ で極値を取るか、取らないか、取るならば極大か極小かが分かる、ということです。

先の通り、この定理の証明は次回行います。

実対称行列の正値性、負値性、不定符号

さて、では定理0.の主張を理解するために実対称行列の正値性、負値性、不定符号について解説します。

実対称行列の正値性、負値性、不定符号

$A=\left( a_{ij}\right)$ を

$(n,n)$ 型の実対称行列とする。このとき

$A$ が正値であるとは、 $A$ の固有値が全て正であるときをいう。
$A$ が負値であるとは、 $A$ の固有値が全て負であるときをいう。
$A$ が不定符号であるとは、 $A$ の固有値に正のもの、負のものがあるときをいう。

ここでも固有値が出現します。
【線型代数学の基礎シリーズ】でも述べたように、固有値は誠にシンプルなコンセプトでありながら、同時に誠に情報量が多いコンセプトでもあります。

さて、正値、負値については特に問題はないかと思いますが、不定符号については少々混乱するかもしれませんので、簡単にではありますが、例を挙げます。

例4. $\displaystyle A= \begin{pmatrix} 2&0\\ 0&3 \end{pmatrix}$ としたとき、固有値を求めて $A$ が正値か負値か不定符号かを判定してみましょう。

ここで、以下の事実を思い出すと計算するまでもないことが分かります。
勿論、正直に計算してもOKです。

定理5.

$n$ 次正方行列

$A$ が三角行列である時、

$A$ の固有値全体は重複も込めて

$A$ の対角成分と一致する。

定理5.の証明は【線型代数学の基礎シリーズ】固有値編その1を御覧ください。

さて、 $A$ は対角行列ですので、三角行列です。
故に $A$ の固有値は $2,3$ です。
従って、 $A$ の固有値は全て正の値なので、 $A$ は正値です。

例6. $\displaystyle B= \begin{pmatrix} -1&0\\ 0&-2 \end{pmatrix}$ としたとき、固有値を求めて $B$ が正値か負値か不定符号かを判定してみましょう。

これも例4.と同様に定理5.から固有値が $-1,-2$ だと直ちに分かります。
故に $B$ の固有値は全て負の値なので、 $B$ は負値です。

例7. $\displaystyle C= \begin{pmatrix} 5&0\\ 0&-2 \end{pmatrix}$ としたとき、固有値を求めて $C$ が正値か負値か不定符号かを判定してみましょう。

これも例4.と例6.と同様に定理5.から固有値が $5,-2$ だと直ちに分かります。
故に $C$ の固有値は正のもの、負のもの双方あるので、 $C$ は不定符号です。

例8. $\displaystyle D= \begin{pmatrix} 3&0\\ 0&0 \end{pmatrix}$ としたとき、固有値を求めて $B$ が正値か負値か不定符号かを判定してみましょう。

これも同様に定理5.から固有値が $3,0$ だと直ちに分かります。
しかし、固有値が全て正というわけでも、全て負というわけでも、不定符号というわけでもありません(負の固有値を持たないから)。
故に、 $D$ は正値でも負値でも不定符号でもないのです。

なぜヘッセ行列の符号が極大極小と関係があるんですか？

先程実対称行列の符号について解説しましたが、「ヘッセ行列の符号で極値が判定できるんだー。ふーん。でもなんで？」となってるかと思います。
これを一撃でイメージが膨らむ定理があります。

と、その定理を説明する前に二次形式について話ます。

二次形式

二次形式というのは比較的シンプルなコンセプトです。

二次形式

$\displaystyle\boldsymbol{x}= \left( \begin{array}{c} x_1\\ \vdots\\ x_n\end{array} \right)\in\mathbb{R}^n$ について、２次の項だけからなる実数係数の整式

$f(\boldsymbol{x})=\sum_{i=1}^na_{ii}x_i^2+2\sum_{i<j}a_{ij}x_ix_j$ を実二次形式という。ここで、

$i>j$ のとき、

$a_{ij}=a_{ji}$ とおくと、

$A=\left( a_{ij}\right)$ は実対称行列となり、

$f(\boldsymbol{x})=\boldsymbol{x}^\top A\boldsymbol{x}=\left(\boldsymbol{x},A\boldsymbol{x} \right)=(A\boldsymbol{x},\boldsymbol{x})$ と表される。

例9. $3x_1^2-2x_1x_2+4x_2^2$ は二次形式です。
実際、
$\begin{eqnarray} 3x_1^2-2x_1x_2+4x_2^2&=& \left( x_1\ x_2\right) \begin{pmatrix} 3&-1\\ -1&4 \end{pmatrix} \left( \begin{array}{c} x_1\\ x_2 \end{array} \right) \end{eqnarray}$
となるからです。

実対称行列の符号と二次形式の符号との関係

では、行きましょう。

定理10.(実対称行列の符号と2次形式の符号)

$A=\left( a_{ij}\right)$ が

$n$ 次実対称行列とするとき、次の1.、2.、3.が成り立つ。

$A$ が正値 $\ \Longleftrightarrow\ \forall \boldsymbol{h}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}$ に対して、 $\left( A\boldsymbol{h},\boldsymbol{h}\right)>0$ 。
$A$ が負値 $\ \Longleftrightarrow\ \forall \boldsymbol{h}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}$ に対して、 $\left( A\boldsymbol{h},\boldsymbol{h}\right)<0$ 。
$A$ が不定符号 $\ \Longrightarrow\ (\exists \boldsymbol{h},\boldsymbol{h}^\prime\in\mathbb{R}^n)\ {\rm s.t.}\ \left(A\boldsymbol{h},\boldsymbol{h} \right)>0,\ \left(A\boldsymbol{h},\boldsymbol{h} \right)<0$ 。

この定理の証明は実対称行列の性質を使えばなんてことありません。

定理10.の証明

$A$ は実対称行列ですので、次の定理を使うことができます。

定理11.

$n$ 次実正方行列

$A$ に対して、次の２つの条件は同値である。

$A$ は対称行列である。
$A$ は適当な直交行列 $P$ によって対角化できる。

$P^{-1}AP= \begin{pmatrix} \lambda_1&&\huge{O}\\ &\ddots&\\ \huge{O}&&\lambda_n \end{pmatrix}$

定理11.の証明は【線型代数学の基礎シリーズ】固有値編その4を御覧ください。

$A$ は実対称行列なので、 $A$ の固有値を $\lambda_1,\dots,\lambda_n$ とすると、定理11.からある実直交行列 $U$ が存在して、
$U^\top AU= \begin{pmatrix} \lambda_1&&\huge{0}\\ &\ddots&\\ \huge{0}&&\lambda_n \end{pmatrix}$
と対角化できます。
このとき、 $\boldsymbol{x}=U\boldsymbol{y}$ (もしくは $U$ が行列であるから $\boldsymbol{y}=U^\top\boldsymbol{x}$ )とおくと、
$\begin{eqnarray} \left( A\boldsymbol{x},\boldsymbol{x}\right)&=&\left( AU\boldsymbol{y},U\boldsymbol{y}\right)\\ &=&\left(U^\top AU\boldsymbol{y},\boldsymbol{y} \right)\\ &=& \left( \begin{pmatrix} \lambda_1&&\huge{0}\\ &\ddots&\\ \huge{0}&&\lambda_n \end{pmatrix},\boldsymbol{y} \right)\\ &=&\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2 \end{eqnarray}$
となります。
ここで、 $\boldsymbol{x}=\boldsymbol{0}\Leftrightarrow\boldsymbol{y}=\boldsymbol{0}$ であることに注意します。

1.の証明

①( $\Rightarrow$ )の証明

$A$ が正値だとします。
このとき $A$ の固有値 $\lambda_1,\dots,\lambda_n$ が全て正です。
今、
$\left( A\boldsymbol{x},\boldsymbol{x}\right)=\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2$
だったわけですので、任意の $\boldsymbol{y}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}$ に対して、 $y_i^2>0\ (1\leq i\leq n)$ が成り立っていて、かつ $\lambda_i>0\ (1\leq i\leq n)$ です。
故に、
$\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2>0$
ですから、 $\left( A\boldsymbol{x},\boldsymbol{x}\right)>0$ です。

②( $\Leftarrow$ )の証明

逆に、任意の $\boldsymbol{y}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}$ に対して、
$\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2>0$
だったとすれば、 $y_i^2>0\ (1\leq i\leq n)$ ですので、 $\lambda_1,\dots,\lambda_n$ は全て正でなければなりません。
従って、 $A$ は正値です。

2.の証明

1.と同じです。

$A$ が負値だとします。
このとき $A$ の固有値 $\lambda_1,\dots,\lambda_n$ が全て負です。
今、
$\left( A\boldsymbol{x},\boldsymbol{x}\right)=\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2$
だったわけですので、任意の $\boldsymbol{y}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}$ に対して、 $y_i^2>0\ (1\leq i\leq n)$ が成り立っていて、かつ $\lambda_i<0\ (1\leq i\leq n)$ です。
故に、
$\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2<0$
ですから、 $\left( A\boldsymbol{x},\boldsymbol{x}\right)<0$ です。

②( $\Leftarrow$ )の証明

逆に、任意の $\boldsymbol{y}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}$ に対して、
$\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2<0$
だったとすれば、 $y_i^2>0\ (1\leq i\leq n)$ ですので、 $\lambda_1,\dots,\lambda_n$ は全て負でなければなりません。
従って、 $A$ は負値です。

3.の証明

$A$ が不定符号だとします。
すなわち、 $A$ の固有値は $0$ ではなく、必ず正か負かのいずれかの値を取ります。
今、
$\left( A\boldsymbol{x},\boldsymbol{x}\right)=\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2$
だったわけですので、 $y_i$ の値によっては $\left(A\boldsymbol{x},\boldsymbol{x}\right)$ は正の値をとったり負の値を取ったりします。

これはつまり、 $\left(A\boldsymbol{h},\boldsymbol{h}\right)>0$ となるような $\boldsymbol{h}\in\mathbb{R}^n$ と $\left(A\boldsymbol{h}^\prime,\boldsymbol{h}^\prime\right)<0$ となるような $\boldsymbol{h}^\prime\in\mathbb{R}^n$ の双方が存在する、ということです。
従って、成り立ちます。

ちなみに、この逆は成り立ちません。
というもの、例えば $A$ が３次の実対称行列だったとして、 $\left( A\boldsymbol{x},\boldsymbol{x}\right)=\lambda_1y_1^2+\lambda_2y_2^2+\lambda_3y_3^2$ と書けたとします。
しかしながら、 $\lambda_1=\lambda_2=0$ だったとしても、 $\lambda_3$ の値によっては $\left( A\boldsymbol{x},\boldsymbol{x}\right)>0$ となったり $\left( A\boldsymbol{x},\boldsymbol{x}\right)<0$ となったりするからです。

定理10.の証明終わり

で、結局どうしてヘッセ行列の符号が極値と関係あるんですか？

さて、少々確認しておくと、 $f^\prime(\boldsymbol{a})\boldsymbol{h}=\boldsymbol{0}$ のとき、
$\begin{eqnarray} f(\boldsymbol{a}+\boldsymbol{h}) &=&f(\boldsymbol{a})+\frac{1}{2}\left( H(\boldsymbol{\boldsymbol{a}+\theta\boldsymbol{h}})\boldsymbol{h},\boldsymbol{h}\right)\\ \end{eqnarray}$
と書けるのでした。
ということは、 $\left( H(\boldsymbol{a}+\theta\boldsymbol{h}),\boldsymbol{h}\right)$ の符号によって $f(\boldsymbol{a})$ と $f(\boldsymbol{a}+\boldsymbol{h})$ の大小関係が分かります。

※以降の話はあくまでイメージを伝えるものですので、厳密ではありません。厳密な話は次回の証明で行います。

もし仮に $\left( H(\boldsymbol{a}+\theta\boldsymbol{h}),\boldsymbol{h}\right)>0$ なのであれば、 $f(\boldsymbol{a}+\boldsymbol{h})>f(\boldsymbol{a})$ となるので、 $f$ は $\boldsymbol{a}$ 極小を取ります。

仮に $\left( H(\boldsymbol{a}+\theta\boldsymbol{h}),\boldsymbol{h}\right)<0$ なのであれば、 $f(\boldsymbol{a}+\boldsymbol{h})<f(\boldsymbol{a})$ となるので、 $f$ は $\boldsymbol{a}$ 極大を取ります。

不定符号だった場合は大小が定まらないので極値は取らない、というイメージです。

余談(読者の皆様のコメントを下さい！)

今回の話は解析の話をしていると思いきや、実は線型代数の話の方がウエイトが多くなっています。
筆者の体験談だと「あれ？今まで解析の話をしてたのに気がついたら代数じゃね？」ということが割とあります。

そういう意味で行くと、やはり数学はつながっているんだなあ、と感じます。
例えば、幾何の問題を解析的な手法で解くとか。
それで言うと、デカルト座標系上で幾何学を考えて、辺の長さやらの量を定めてより図形に情報量を与える、というのがいい例かもしれません。

読者の皆さんで「この問題は一見〇〇の分野の問題に見えて、実は△△の知識を使うと一瞬で片がつく」という問題に出会った方がいれば是非、コメントで教えて下さい！

結

今回はヘッセ行列による極値判定①ということで、ヘッセ行列での極値判定に必要な準備を説明しました。
具体的にはヘッセ行列とはなにか、実対称行列の正値性、負値性、不定符号性について解説しました。
実は、殆ど線型代数の話です(“行列”って言ってるんだからそりゃそうだろって感じですが(笑))。

そして、簡単にではありますが、ヘッセ行列の”符号”がどうして極値と関係するのか、ということについても解説しました。

次回は定理0.の証明を行い、実際に極値を求めてみます。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

Twitterでもリプ、DM問わず質問、コメントを大募集しております！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

本記事の内容

こんな問題を考えたいのです。

内点a\boldsymbol{a}で極値を取ればf′(a)=0f^\prime(\boldsymbol{a})=\boldsymbol{0}です。

極値って何ですか？

全微分可能な関数が内点で極値を取れば、全微分係数は00です。

定理1.の証明

定理1.の証明終わり

ヘッセ行列の符号によって極値かどうかを判定できる場合があります。

ヘッセ行列？

で、ヘッセ行列って何ですか？

今回と次回のメインとなる定理(証明は次回行います)

今回と次回のメインとなる定理(ヘッセ行列の符号による極値の判定)

実対称行列の正値性、負値性、不定符号

なぜヘッセ行列の符号が極大極小と関係があるんですか？

二次形式

実対称行列の符号と二次形式の符号との関係

定理10.の証明

1.の証明

2.の証明

3.の証明

定理10.の証明終わり

で、結局どうしてヘッセ行列の符号が極値と関係あるんですか？

余談(読者の皆様のコメントを下さい！)

結

コメントをする

内点 $\boldsymbol{a}$ で極値を取れば $f^\prime(\boldsymbol{a})=\boldsymbol{0}$ です。

全微分可能な関数が内点で極値を取れば、全微分係数は $0$ です。