本記事の内容
本記事は、基本情報技術者試験における2進数の四則演算、シフト演算について、情報及びコンピュータの素人目線から説明する記事です。
本記事を読むに当たり、論理演算について知っている必要があるため、以下の記事も合わせてご覧ください。

イントロ
CPU(※)の内部は無数の電子回路によって構成されています。
この電子回路はとても小さくて、電子回路の幅を髪の毛くらいに拡大すれば、CPUの大きさは東京ディスニーランドと同じくらいの大きさになります。
ちなみに、CPUの大きさは指でつまめるくらいです。(ご興味があれば調べてみてください)
※CPU
詳しくはのちの記事で述べますが、CPUを人間の臓器に例えれば「脳」です。コンピュータにあらゆる命令を下す部品がCPUです。
「CPUが脳みそだったとすると、PCの図体からして脳がちっちゃいのに随分と頭いいな、コンピュータって」と思いました。
論理回路
論理回路
論理回路とは、論理演算を行う電子部品である。論理演算とは、AND、OR、XOR、NOTでしたね。
コンピュータの脳みそたるCPU(中央処理装置※後の記事で述べます)は非常に多くの論理回路を使って演算をしています。
MIL記号
実物の論理回路は電子部品なわけですが、論理回路を紙面上に表す際の記号をMIL記号(みるきごう)といいます。
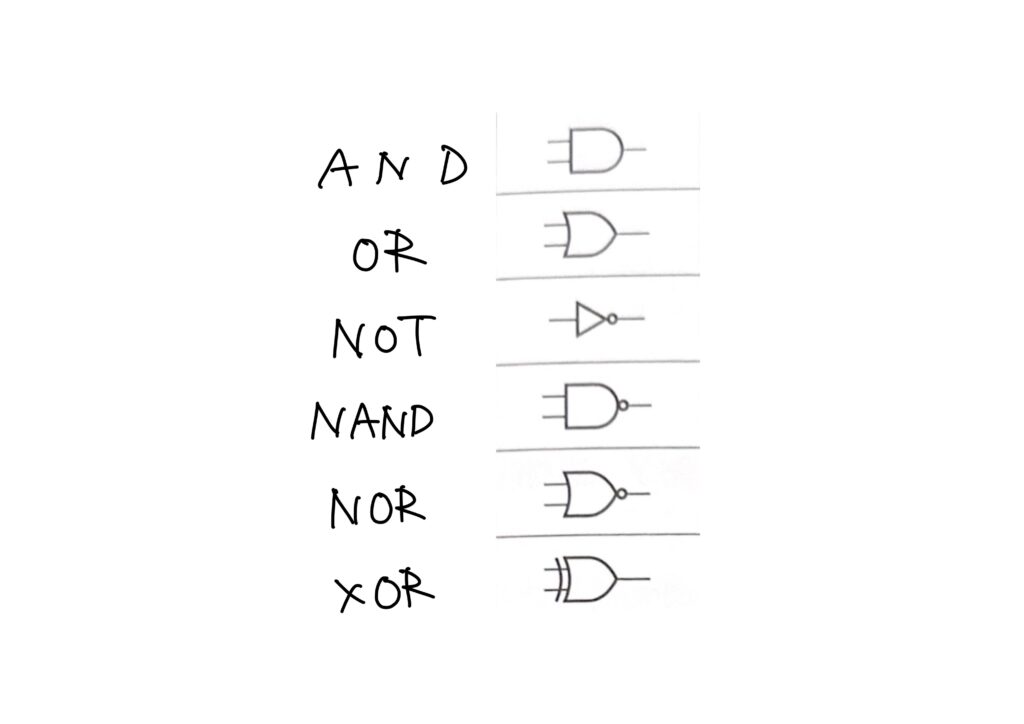
以下に、主たるMIL記号を列挙しますが、記号を覚える必要はありません。
なぜかというと、問題用紙に必ず記法の意味が掲載されるからです。(覚えちゃったほうが早いですが、覚えなくてOKです)
ただ、記号の意味は覚える必要があります。
「ANDってなんだったけなあ」というのは覚える必要がある、という意味です。
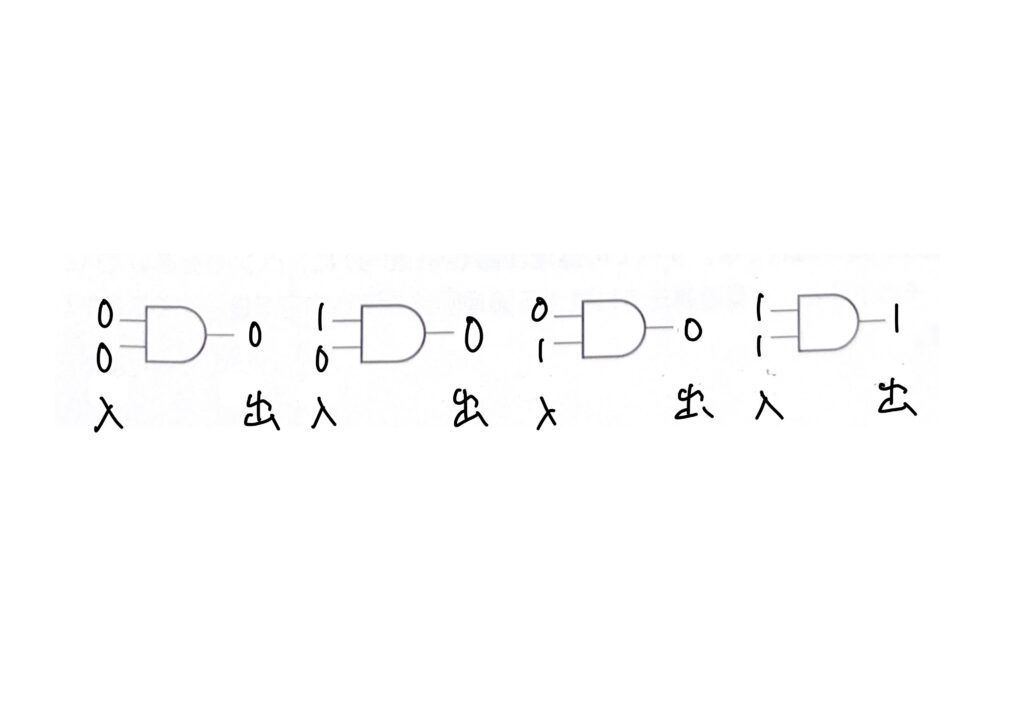
MIL記号による論理積の演算を例としてみてみましょう。
論理回路の問題の解き方
図の論理回路と等価な回路はどれか。
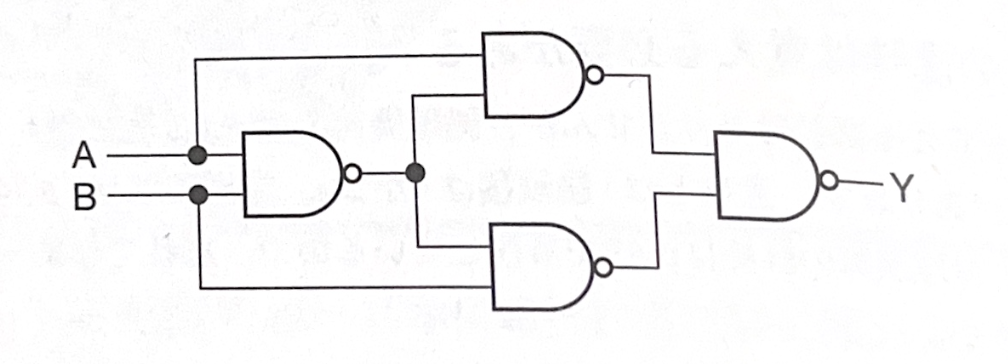
回答の形式としては、設問の論理回路と同じ意味を持つMIL記号、論理式、真理値表のいずれかを選択する問題として出題されます。
論理回路の問題はベン図で
論理回路の問題は複雑に見えますが、ベン図で処理することで視覚的にもわかりやすく解くことが出来ます。

以上のことから、排他的論理和(XOR)と同じベン図になっている事がわかるので、答えは3.です。
一つずつ、地道にやると簡単に解けます。
加算回路
今まで学習した論理回路を組み合わせることで、ようやくCPUは足し算ができるようになります。
つまり、この節ではCPUがどのようにして足し算をしているかがわかります。
加算回路
2進数の足し算を行う論理回路を加算回路という。加算回路には、
- 半加算器
- 全加算器
の2種類が存在します。
半加算器
半加算器
半加算器は、2進数の足し算において、下の位からの桁上りを考慮しない加算回路を指す。文章だとわかりにくいので、具体的な値で考えてみます。
2進数は0と1の2種類の数しか使わないので、2つの2進数の足し算は本質的には
- \(0+0=1\)
- \(0+1=1\)
- \(1+0=1\)
- \(1+1=10\)
の4種類だけです。

これら4つの演算を、4つの文字(X、Y、C、S)を使ってX+Y=CSと表現したとします。
これを真理値表に表すと次です。
| 入力 | 入力 | 出力 | 出力 |
| X | Y | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
この半加算器の真理表は、論理積(AND)と排他的論理和(XOR)を組み合わせで作ることが出来ます。
以下が半加算器の論理回路です。
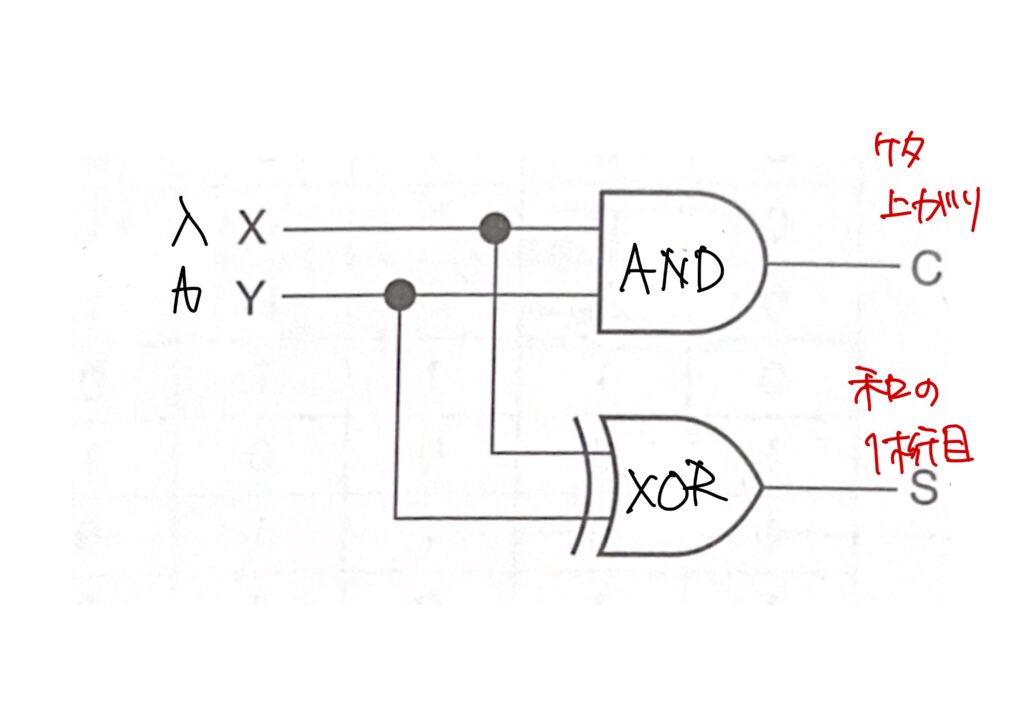
全加算器
全加算器は、半加算器が下の位からの桁上りを考慮しない加算回路であったのに対し、桁上りを考慮する加算回路です。
全加算器
下の位からの桁上りを考慮する加算回路を全加算器という。半加算器の入力は2つでしたが、全加算器は桁上りの分の情報が増えるため、3つの入力が必要になります。
3つの2進数の足し算は以下の8パターンです。
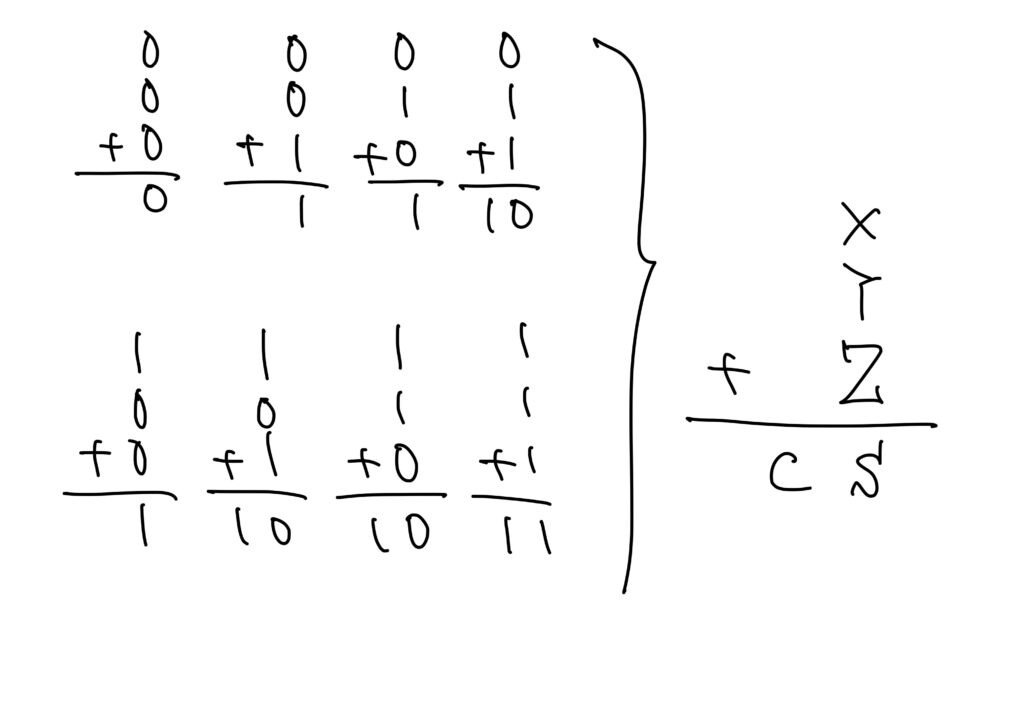
この8つの計算を、半加算器のときと同様にして5つの記号(X、Y、Z、C、S)を使って真理値表に表すと次です。
| 入力 | 入力 | 入力 | 出力 | 出力 |
| X | Y | Z | C | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
全加算器の真理値表は、2つの半加算器と、1つの論理和(OR)の組み合わせで作ることが出来ます。
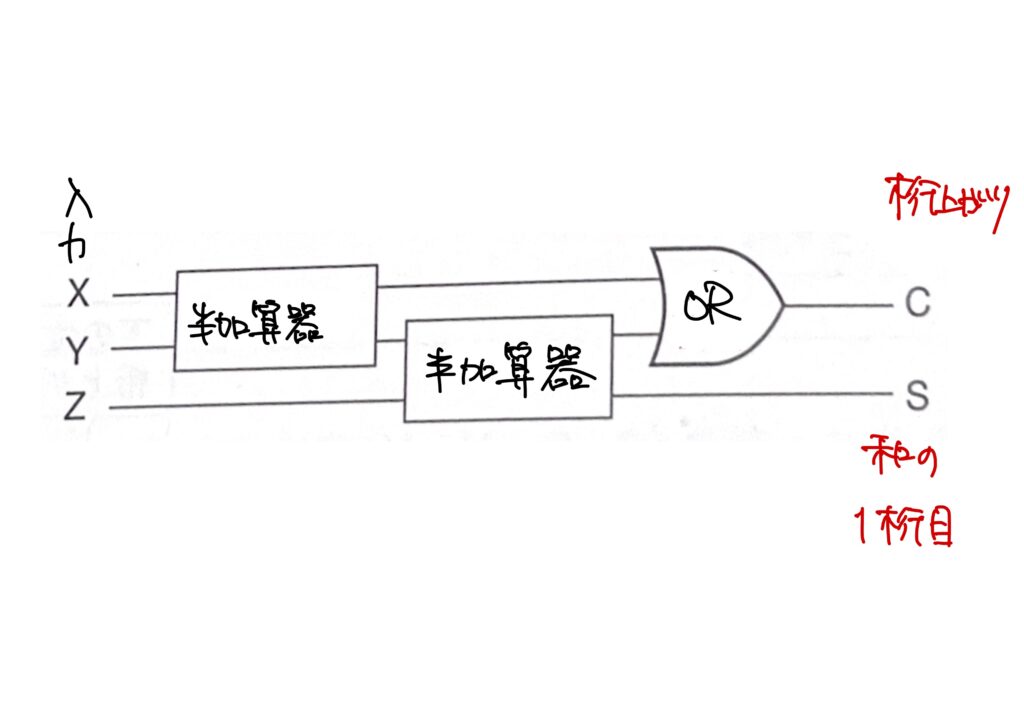
結
今回は、基本情報技術者試験における論理回路について、情報及びコンピュータの素人目線から説明しました。
問題が解けるということに重きを置き説明しました。
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
Twitterでもリプ、DM問わず質問、コメントを大募集しております!



コメントをする