本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
では、問題
次の不等式で表される空間図形はどんな形でしょうか。図示してください。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p18.
$$
\left|x+y+z\right|+\left|-x+y+z\right|+\left|x-y+z\right|+\left|x+y-z\right|\leq4
$$
(ヒント) \(\left|X\right|=\max\left( X,-X\right)\)
いざ、チャレンジ
チャレンジの結果…解けました。
今回も特に難しくはないですが、目の付け所によっては計算量が膨大になってしまう問題でした。
また、空間図形を描く力が問われている問題でもあると思います。
筆者の解答
この問題を見た瞬間に「なーんだ。3次元空間を第1象限から第8象限で場合分けすればいいじゃん」と思いました。
その8つの場合とは、以下です。
- \(x\geq0,\quad y\geq0,\quad z\geq0\)
- \(x>0,\quad y>0,\quad z<0\)
- \(x>0,\quad y<0,\quad z>0\)
- \(x>0,\quad y<0,\quad z<0\)
- \(x<0,\quad y>0,\quad z>0\)
- \(x<0,\quad y>0,\quad z<0\)
- \(x<0,\quad y<0,\quad z>0\)
- \(x<0,\quad y<0,\quad z<0\)
この8つの場合を紙に書くまで「計算すりゃ求まるんでしょ?」と思いましたが、実際に書いてみると「これは計算ミスを誘発するし手間がかかるな」と思い、やめました。
とはいえ、本質的にはこの手法ですので、問題文の式を見直してみました。
$$
\left|x+y+z\right|+\left|-x+y+z\right|+\left|x-y+z\right|+\left|x+y-z\right|\leq4
$$
そうすると、\(x,y,z\)でそれぞれ1個ずつ符号が変わっているということに気が付きました。
となれば話は簡単で、第1象限でだけ考えて、後は軸について対称だということになります。
故に、8つ考える必要はなく、1つの場合だけ考えれば良いということになります。
後は、第1象限を以下の4つの場合に分けて調べれば良いだけです。
- \(x\geq y+z\)
- \(y\geq x+z\)
- \(z\geq x+y\)
- \(x\leq y+z,\quad y\leq x+z,\quad z\leq x+y\)
- \(x\geq y+z\)のとき
- \(\left|x+y+z\right|=x+y+z\)
- \(\left|-x+y+z\right|=x-y-z\)
- \(\left|x-y+z\right|=x-y+z\)
- \(\left|x+y-z\right|=x+y-z\)
- \(y\geq x+z\)のとき
- \(\left|x+y+z\right|=x+y+z\)
- \(\left|-x+y+z\right|=-x+y+z\)
- \(\left|x-y+z\right|=-x+y-z\)
- \(\left|x+y-z\right|=x+y-z\)
- \(z\geq x+y\)のとき
- \(\left|x+y+z\right|=x+y+z\)
- \(\left|-x+y+z\right|=-x+y+z\)
- \(\left|x-y+z\right|=x-y+z\)
- \(\left|x+y-z\right|=-x-y+z\)
- \(x\leq y+z,\quad y\leq x+z,\quad z\leq x+y\)のとき
- \(\left|x+y+z\right|=x+y+z\)
- \(\left|-x+y+z\right|=-x+y+z\)
- \(\left|x-y+z\right|=+x-y+z\)
- \(\left|x+y-z\right|=x+y-z\)
これらの場合について、問題の不等式は
- \(x\leq 1\)
- \(y\leq 1\)
- \(z\leq 1\)
- \(x+y+z\leq 2\)
と書き換えることができます。
故に、第1象限における図形は次になります。

どうやってこの図を描いたのか?というと、代表的な値を代入して、その値をもとに描きました。
したがって、解答は

です。
投稿されたエレガントな解答
(前略)
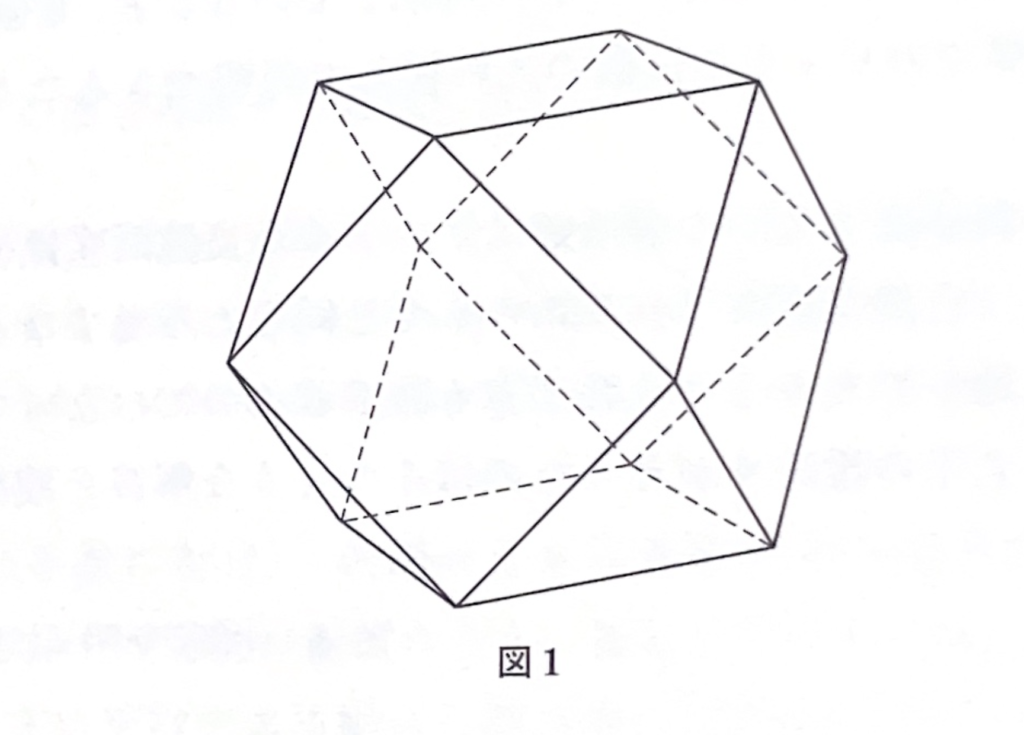
成績は校長で、図形を図示することについては、ほとんどすべてが正解であった。(図1、正解図)
(中略)
寄せられた解答を分類すると次のようになる。
場合分け法1
式の観察から求める図形は各座標平面について対称である。したがって、図形を調べるには、第1象限(\(x\geq0,\ y\geq0,\ z\geq0\))の場合を調べればよい。そうすると、\left|\right|の中の式の符号による8通りの場合分けが考えられる。(中略)
場合分け法2
(中略)特殊な場合に帰着する方法
式の対称性から、\(x\geq y\geq z\geq0\)の場合だけ調べればよい。この場合でも、さらに
(1)\(x\geq y+z\)
(2)\(x\leq y+z\)
の場合分けが必要になる。連立不等式
\(\left|X\right|=\max\left( X,X\right)\)であることから、4数の\left|\right|の和\(\left|W\right|+\left|X\right|+\left|Y\right|+\left|Z\right|\)は\(\pm W\pm X\pm Y\pm Z\)という形の16数のうちのさ最大数を意味する。16数の最大数が4以下であるということは、16数のすべての数が4以下であるということと同じである。
したがって、課題の不等式は、16個の不等式
$$
\pm\left( x+y+z\right)\pm\left( -x+y+z\right)\pm\left( x-y+z\right)\pm\left( x+y-z\right)\leq4
$$
から成る連立不等式と同値である。このうち、2個が無条件に成り立つ不等式\(0\leq 4\)で、のこりの14個の不等式が立方八面体の14個の面と対応する。これらの不等式を整理すると図形が決まる。(中略)
max計算
一般に、絶対値の和について、
$$
\left|X\right|+\left|Y\right|=\max\left(\left|X+Y\right|,\left|X-Y\right| \right)
$$
だから、
\begin{eqnarray}
&&\left|x+y+z\right|+\left|-x+y+z\right|+\left|x-y+z\right|+\left|x+y-z\right|\\
&&=\max\left( 2|x|,2|y+z|\right)+\max\left( 2|x|,2|y-z|\right)\\
&&=\max 4|x|,2|x|+2|y+z|,\\
&&\quad\quad 2|x|+2|y-z|,|y+z|+|y-z|).
\end{eqnarray}
ここで、
\begin{eqnarray}
&&\max(|x|+|y+z|,|x|+|y-z|)\\
&&=|x|+\max(|y+z|,|y-z|)=|x|+|y|+|z|\\
&&|y+z|+|y-z|=\max\left( 2|y|,2|z|\right).
\end{eqnarray}
よって、
\begin{eqnarray}
&&\left|x+y+z\right|+\left|-x+y+z\right|+\left|x-y+z\right|+\left|x+y-z\right|\\
&&=\max\left(4|x|,4|y|,4|z|,2\left( |x|+|y|+|z|\right) \right).
\end{eqnarray}
このことから、与えられた不等式は、
$$
|x|\leq1,\quad |y|\leq1,\quad |z|\leq1,\quad |x|+|y|+|z|\leq2
$$
と同値である。最初の3つの不等式はある立方体を表し、最後の不等式はある正八面体を表す。求める図形はこれらの共通部分である。(後略)
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p134-p137.
読者の皆様への挑戦状!
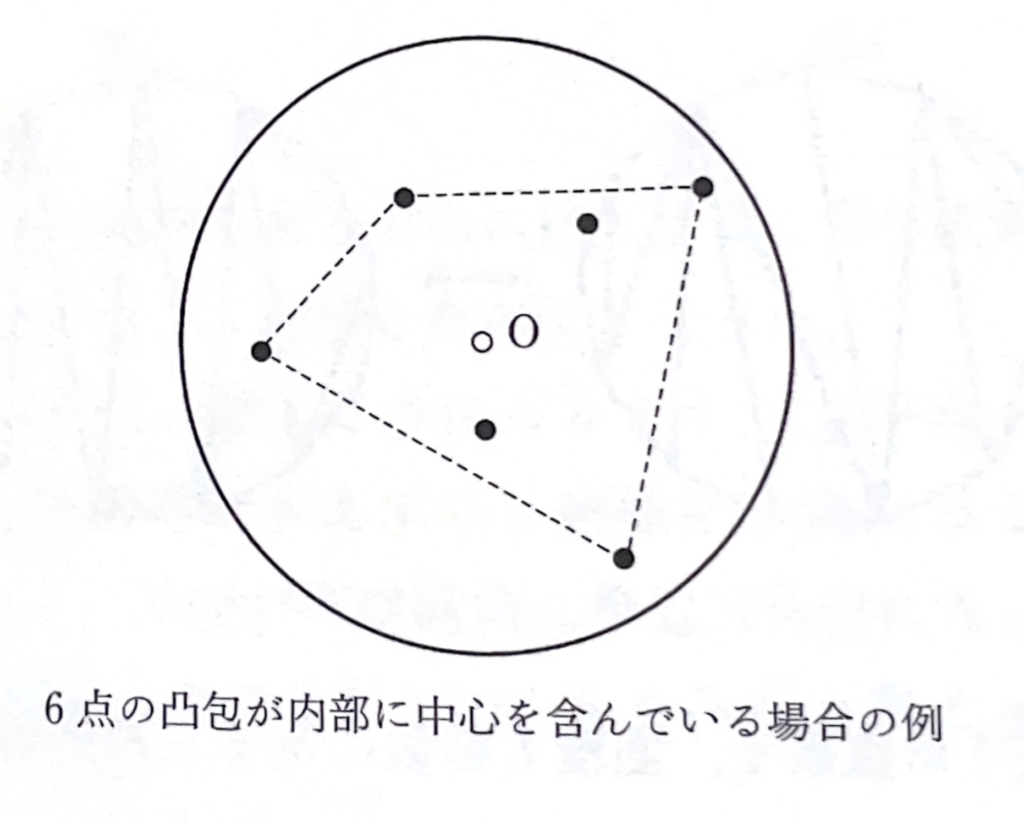
平面上の円盤内から、一様な確率密度(ある領域から点が選ばれる確率はその領域の面積に比例すること)に従い、ランダムに選ばれた\(n\)個の点があるとします。この\(n\)個の点の凸包(この\(n\)個の点を含む最小の凸集合、すなわち\(n\)個の点のうちのいくつかを頂点とし、残りの点を内部に含む凸多角形)の内部に、この円盤の中心\(O\)が含まれる確率はいくらでしょうか。
できればこの問題の「平面」を「空間」に、「円盤」を「球」に換えてできる同様の問題についても確率を求めて下さい。さらに、一般次元にまで拡張した問題も考察してみて下さい。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p18.
前回の問題は【1時間チャレンジシリーズ】挑戦⑲を御覧ください。
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!




コメントをする