本記事の内容
本記事は、可解群の重要な性質について解説する記事です。
本記事を読むに当たり、可解群とベキ零群について知っている必要があるため、以下の記事も合わせて御覧ください。
ちょっとした復習(生成された部分群、交換子、交換子群)
生成された部分群
語(word)
\(G\)を群、\(S\subset G\)とする。\(x_1,\dots,x_n\in S\)により\(x_1^{\pm1}\cdots x_n^{\pm1}\)という形をした\(G\)の要素を\(S\)の要素による語(word)という。ただし、\(n=1\)ならば\(x_1^{\pm1}\cdots x_n^{\pm1}\)は単位元\(1_G\)を表すとし、\(\pm1\)は各\(x_i\)ごとに\(1\)か\(-1\)のどちらでも良いとする。
ここで、\(x_i^{\pm1}\)という記号ですが、\(x_i^{+1}\)は\(x_i\)そのものを意味し、\(x_i^{-1}\)は\(x_i\)の逆元を意味しています。
このとき、次が成り立ちます。
定理1.
\(\langle S\rangle\)を\(S\)の要素による語全体の集合とするとき、次の1.、2.が成り立つ。- \(\langle S\rangle\)は\(G\)の部分群である。
- \(H\)が\(G\)の部分群で\(S\)を含むならば、\(\langle S\rangle\subset H\)である。すなわち、\(\langle S\rangle\)が\(S\)を含むような最小の部分群である。
定理1.の証明は【代数学の基礎シリーズ】群論編 その2を御覧ください。
生成された部分群、生成系、生成元
\(\langle S\rangle\)を\(S\)の要素による語全体の集合とするとき、\(\langle S\rangle\)を\(S\)によって生成された部分群、\(S\)のことを生成系、\(S\)の要素を生成元という。交換子、交換子群
交換子、交換子群
\(G\)を群とする。- 交換子 \(a,b\in G\)に対して、\([a,b]=aba^{-1}b^{-1}\)と定め、これを\(a,b\)の交換子という。
- 交換子群 \(H_1,H_2\subset G\)が部分群ならば、\(\left\{[a,b]\middle|a_in_1,\ b\in H_2\right\}\)で背性される\(G\)の部分群を\(\left[ H_1,H_2\right]\)と書く。
$$ D(G)=\left[ G,G\right] $$ を\(G\)の交換子群という。
詳しくは【代数学の基礎シリーズ】群論編 その20を御覧ください。
交換子列
交換子列というものを導入します。
交換子列
\(G\)を群とする。 $$ D_1(G)=\left[G,G\right],\quad D_{i+1}(G)=\left[D_i(G),D_i(G)\right]\ (i=1,2,\cdots) $$ と定めれば、 $$ G\supset D_1(G)\supset D_2(G)\supset \cdots $$ である。これを\(G\)の交換子列という。可解群の重要な性質(群が可解群であるための必要十分条件)
本題です。
命題2.
群\(G\)が可解群であることと、\(D_n(G)=\left\{1_G\right\}\)となる\(n\)が存在することは同値である。命題2.の証明
\(G=G_0\supset G_1\supset \cdots\supset G_n=\left\{1_G\right\}\)を、\(i=1,2,\dots,n-1\)に対して、\(G_{i+1}\triangleleft G_i\)で\(G_i/{G_{i+1}]\)が可換群となるような部分群の列とします。
\(G_i/{G_{i+1}}\)が可換群なので、\(D(G_i)\subset G_{i+1}\)です。
したがって、帰納的に\(D_i(G)\subset G_i\)です。
\(G_n=\left\{1_G\right\}\)なので、\(D_n(G)=\left\{1_G\right\}\)です。
逆に、\(D_n(G)=\left\{1_G\right\}\)とします。
\(G_0=G\)とし、\(i=1,\dots,n\)に対して\(G_i=D_i(G)\)とします。
すると、\(G=G_0 \supset G_1\supset \cdots\supset G_n=\left\{1_G\right\}\)です。
交換子群は正規部分群なので、\(G_{i+1}\triangleleft G_i\ (i=0,\dots,n-1)\)です。
さらに、\(G_i/{G_{i+1}}=G_i/{\left[ G_i,G_i\right]}\)は可換なので、\(G\)は可解群です。
命題2.の証明終わり
皆様のコメントを下さい!
今回から数回、ちょっとした数学のコラムを書いていきます。
初回は可能無限と実無限です。
無限に対する考察は古代ギリシャに始まります。
古代ギリシャでは無限について非常に多くの議論がなされましたが、最初に「無限」について考察したのは、タレス(Thales、紀元前624年–紀元前546年頃)の弟子であるアナクシマンドロス(Anaximandros 610BC–547BC)だといわれています。
そして最終的に主流となったのはアリストテレス(Aristotle (384 BC–322 BC))の考え方です。
アリストテレスは可能性としての無限(可能無限 potential infinity)しか認めず、現実的な無限(実無限 actual infinity)を認めませんでした。
アリストテレスによれば、実際に無限の大きさを持つ物体は存在しません。
宇宙も有限であり、地球を中心とする同心球面による層状をしていて、その外側には何もありません。
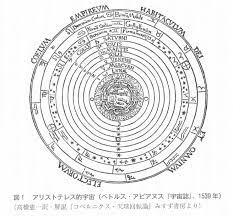
この宇宙観(天動説)はトレミー(クラウディオス・プトレマイオ ス Claudius Ptolemaeus;83年頃–168 年頃)により精密化されましたが、後に正しくないことがコペルニクス(1473–1543)により明らかになります。
ジョルダーノ・ブルーノ(Giordano Bruno, 1548–1600)はコペ ルニクスの地動説を支持し、さらに宇宙は無限であると主張したため異端であるとの判決を受けましたが、決して自説を撤回しなかったため火刑に処せられました。
しかし、この世の中に無限のものが存在するのか、宇宙が有限で「閉じて」いるかどうかは現在でも不明です。
森羅万象を適切に説明する数学的モデルは実無限の観点から構成されてはいますが、現実に無限が存在するかという問に答えるものではありません。
- 実無限:無限の対象の全体性を把握して、無限が実際に存在しているとする立場。
- 可能無限:無限を把握出来るのは、限りがないということを確認する操作が存在していることだけで、無限全体というのは認識出来ないとする立場。
国語辞典での自然数の定め方は、可能無限の立場を取っています。
如何でしたか?
数学では”無限”を考えますが、それについて実は深く語ることは少ないと思います。
それを踏まえて今回は古代ギリシアから考察されてきた無限についてコラムとしてお伝えしました。
ここに書かれれいることの他に無限についての歴史についてご存知のことがあれば是非コメントで教えて下さい!
結
今回は、可解群の重要な性質として、交換子の列が単位元飲みからなる集合に必ず有限回で行き着くという事実を解説しました。
可解群の重要な性質で、これは後に方程式論、特に5次以上の方程式には解の公式が存在しないという主張の証明に関わってきます。
次回はベキ零群の性質と単純群について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
代数についてより詳しく知りたい方は以下を参考にすると良いと思います!




コメントをする