(数セミ)”エレガントな解答をもとむ”に1時間で挑戦！【1時間チャンジシリーズ】挑戦⑤

本記事の内容

本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。

本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。

今回は「エレガントな解答をもとむ selections」に掲載されいている問題です。

問題①

今回は整数論の問題です。

先に述べておくと筆者は整数問題は非常に苦手です。
温かい目で御覧ください….

$1$から$80$までの$80$個の数から、$43$個の数を
$$\{1,2,\cdots,11,23,24,\cdots,33,45,46,\cdots,55,67,68,\cdots,76\}$$
のように抜き出すと、その中のどの$2$数をとっても、差は$11$になりません。また、
$$\{1,2,\cdots,12,25,26,\cdots,36,49,50,\cdots,60,73,74,\cdots,79\}$$
のように抜き出すと、どの$2$数の差も$12$になりません。
ところが、$43$個の数をどのように抜き出しても、その中の$2$数をうまく選ぶと、その差を$10$や$13$にできます。その理由を考えてください。
また、$1$から$25$までのそれぞれの数にたいし、その差がうまくできないように$43$個の数を抜き出せるものと、どうしても差ができてしまうものに分けてください。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p10-p11.

いざ、チャレンジ

チャレンジの結果、一部解けましたが全回答するには至りませんでした…
具体的には差が$10$となる部分については回答できました。
恐らく同じ方法で$13$の場合もできます。

さて、では、筆者の解答を紹介します。

筆者の解答

まず、問題文は口語調ですので、何を問われているのか、ということを論理式で書くことにしました。

$N=\{n\in \mathbb{N}\mid 1\leq n\leq 80\}$とします。
このとき

を証明しなさい、ということがこの問題です。
ただし、$\left|A\right|$は集合$A$の要素の数を表していて、$(\forall A\subset N$ satisfying $\left|A\right|=43)$というのは「$\left|A\right|=43$を満たすような任意の$A\subset N$に対して」という意味です。

さて、証明してほしいことが何かが分かりましたが、少々実験してみます。

仮に$1\in A$であれば、差が$10$となる数は$11$ですので、$11\in A$ということになります。
これを表で表してみます。

$b$	$a$		$b$	$a$
1	11		11	21
2	12		12	22
3	13		13	23
4	14		14	24
5	15		15	25
6	16		16	26
7	17		17	27
8	18		18	28
9	19		19	29
10	20		20	30

これを見ると、確かに必ず差が$10$になるペアが存在するっぽいなあ、と思います。
パっと思いついたので、背理法で攻めてみます。
つまり、

として、矛盾を導いていきます。
これはすなわち$x\in A$ならば、$x+10\not\in A$ということですので、

$x=1$のとき	$x+10=11\not\in A$		$x=21$のとき	$x+10=31\not\in A$	$\cdots$	$x=61$のとき	$x+10=71\not\in A$
$x=2$のとき	$x+10=12\not\in A$		$x=22$のとき	$x+10=32\not\in A$	$\cdots$	$x=62$のとき	$x+10=72\not\in A$
$x=3$のとき	$x+10=13\not\in A$		$x=23$のとき	$x+10=33\not\in A$	$\cdots$	$x=63$のとき	$x+10=73\not\in A$
$x=4$のとき	$x+10=14\not\in A$		$x=24$のとき	$x+10=34\not\in A$	$\cdots$	$x=64$のとき	$x+10=74\not\in A$
$x=5$のとき	$x+10=15\not\in A$		$x=25$のとき	$x+10=35\not\in A$	$\cdots$	$x=65$のとき	$x+10=75\not\in A$
$x=6$のとき	$x+10=16\not\in A$		$x=26$のとき	$x+10=36\not\in A$	$\cdots$	$x=66$のとき	$x+10=76\not\in A$
$x=7$のとき	$x+10=17\not\in A$		$x=27$のとき	$x+10=37\not\in A$	$\cdots$	$x=67$のとき	$x+10=77\not\in A$
$x=8$のとき	$x+10=18\not\in A$		$x=28$のとき	$x+10=38\not\in A$	$\cdots$	$x=68$のとき	$x+10=78\not\in A$
$x=9$のとき	$x+10=19\not\in A$		$x=29$のとき	$x+10=39\not\in A$	$\cdots$	$x=69$のとき	$x+10=79\not\in A$
$x=10$のとき	$x+10=20\not\in A$		$x=30$のとき	$x+10=40\not\in A$	$\cdots$	$x=70$のとき	$x+10=80\not\in A$

となります。
従って、$x\in A$となる$x$は$40$個しか存在しないので、$\left|A\right|=43$に矛盾です。
しかしながら、これでは論破したことにはなりません。
なぜなら「$x=1\in A$の場合は」の話だからです。
これを全パターン行えば一応、証明はできますが、骨が折れます。

従って別の方法のほうが良さそうです。

ここで、気が付きました。
「こういう整数の問題は剰余類で分けると案外解けるんじゃないか？」と。
ということで、$1$から$80$までの数を$10$で割った余りでグループ分けしてみます。
$X_i$で、$10$で割った余りが$i$であるような$1$から$80$までの自然数の集合を表すことにすると、

$$\begin{eqnarray} X_0&=&\{10,20,30,40,50,60,70,80,\}\\ X_1&=&\{1,11,21,31,41,51,61,71\}\\ X_2&=&\{2,12,22,32,42,52,62,72\}\\ X_3&=&\{3,13,23,33,43,53,63,73\}\\ X_4&=&\{4,14,24,34,44,54,64,74\}\\ X_5&=&\{5,15,25,35,45,55,65,75\}\\ X_6&=&\{6,16,26,36,46,56,66,76\}\\ X_7&=&\{7,17,27,37,47,57,67,77\}\\ X_8&=&\{8,18,28,38,48,58,68,78\}\\ X_9&=&\{9,19,29,39,49,59,69,79\} \end{eqnarray}$$
となります。
$X_i$の中では差が$10$となるペアが存在しますが、異なる剰余類では差が$10$となることはありません。
従って、異なる剰余類からなるべくと多く選び、同じ剰余類からはなるべく少なく選びます。
すると、

• $X_0$からは$\{10,30,50,70\}$かまたは$\{20,40,60,80\}$のいずれか一方
• $X_1$からは$\{1,21,41,61\}$かまたは$\{11,31,51,71\}$のいずれか一方
  $\vdots$

というように選ぶと、$40$個選んだことになります。
しかし、今$43$個選ぶので、もう$3$個余分に選ぶ必要がありますが、これ以上追加すると、必ず差が$10$となるようなペアが必ず存在してしまいます。

では、$13$のときはどうでしょうか？というところで時間切れでした。

解答

筆者の解答と同じ部分については割愛します。
以下に引用する際に出現する$A_i$は筆者の解答における$X_i$です。

（前略）

解答は2通りに大別されます。

（中略）

同じように考えると、$k=13$のときは、13で割った余りが0から12までの13のグループに別れますが、各グループに含まれる個数は違ってきます。$A_1$と$A_2$は
$$\begin{eqnarray} A_1&=&\{1.14.27.40.53.66.79\}\\ A_2&=&\{2,15,28,41,54,67,80\} \end{eqnarray}$$
の7個ずつ、残りは
$$\begin{eqnarray} &&A_3=\{1.14.27.40.53.66.79\},\quad A_4=\{4,17,30,43,56,69\}\\ &&A_5=\{5,18,31,44,57,70\},\quad A_6=\{6,19,32,45,58,71\}\\ &&A_7=\{7,20,33,46,59,72\},\quad \cdots \end{eqnarray}$$
の6個ずつです。このため、26個ずつ離れた数は、$A_1$と$A_2$では4個ずつ、残りの11のグループでは3個ずつとなり、その合計は41$(=4\times 2+3\times 11)$です。このため、42個に増加すると、どのように抜き出しても、差が13になる2数が見つかります。
同じ考え方を$k=1\sim25$のそれぞれに適用すると、抜き出せる最大の個数は、
$$\begin{array}{c} 1\cdots40個&2\cdots40個&3\cdots41個&4\cdots40個\\ 5\cdots40個&6\cdots42個&7\cdots42個&8\cdots40個\\ 9\cdots44個&10\cdots40個&11\cdots44個&12\cdots44個\\ 13\cdots41個&14\cdots42個&15\cdots45個&16\cdots48個\\ 17\cdots46個&18\cdots44個&19\cdots42個&20\cdots40個\\ 21\cdots40個&22\cdots42個&23\cdots46個&24\cdots48個\\ 25\cdots50個&&& \end{array}$$
となります。こうして、43個の数を抜き出すとき、差ができないように抜き出せるのは
$$9,11,12,15,16,17,18,22,23,24,25$$
の11個だけです。

第2の方法は、80までという制限を取り除き、$n_1,n_2,\dots,n_{43}$という43個の数を抜き出して、どの2数の差も$k$とならないようにしたとき、$n_{43}$の最小値はいくらになるかを調べるものです。すると、$k=1$では$1,3,5,\cdots,85$の奇数を抜き出せばよく、$n_{43}=85$です。また、$k>1$では、第1の方法を参照すれば、
$$\begin{array}{c} 1,&2,&3,&\cdots&k,\\ 2k+1,&2k+2,&2k+3,&\cdots&3k,\\ 4k+1,&4k+2,&4k+3,&\cdots&5k,\\ 6k+1,&6k+2,&\cdots& \end{array}$$
のように抜き出すことになり、$\displaystyle\frac{43}{k}$の整数部分を$a$とおけば、
$$n_{43}=2ka+(43-ka)=ka+43,\quad (k>1)$$
となります。この値を計算すると、$k=1\sim25$にたいする$n_{43}$の最小値は、
$$\begin{array}{c} 1\cdots85&2\cdots85&3\cdots85&4\cdots83&5\cdots83\\ 6\cdots85&7\cdots85&8\cdots83&9\cdots79&10\cdots83\\ 11\cdots76&12\cdots79&13\cdots82&14\cdots85&15\cdots73\\ 16\cdots75&17\cdots77&18\cdots79&19\cdots81&20\cdots83\\ 21\cdots85&22\cdots65&23\cdots66&24\cdots67&25\cdots68\\ \end{array}$$
となります。この値は80以下ならば良いので、差ができないように抜き出せるのは、
$$9,1112,15,16,17,18,22,23,24,25$$
の11個だけです。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p67-p69.

第2の方法については、すごいなあ、と思いました。
しっかり一般化できています。
しかし、多少の力技が必要とのことで、もう少し力技でない解答が無いのかなあ、とも思いました。
思いついた方、是非コメントで教えて下さい！

問題②

次は規則性の問題です。

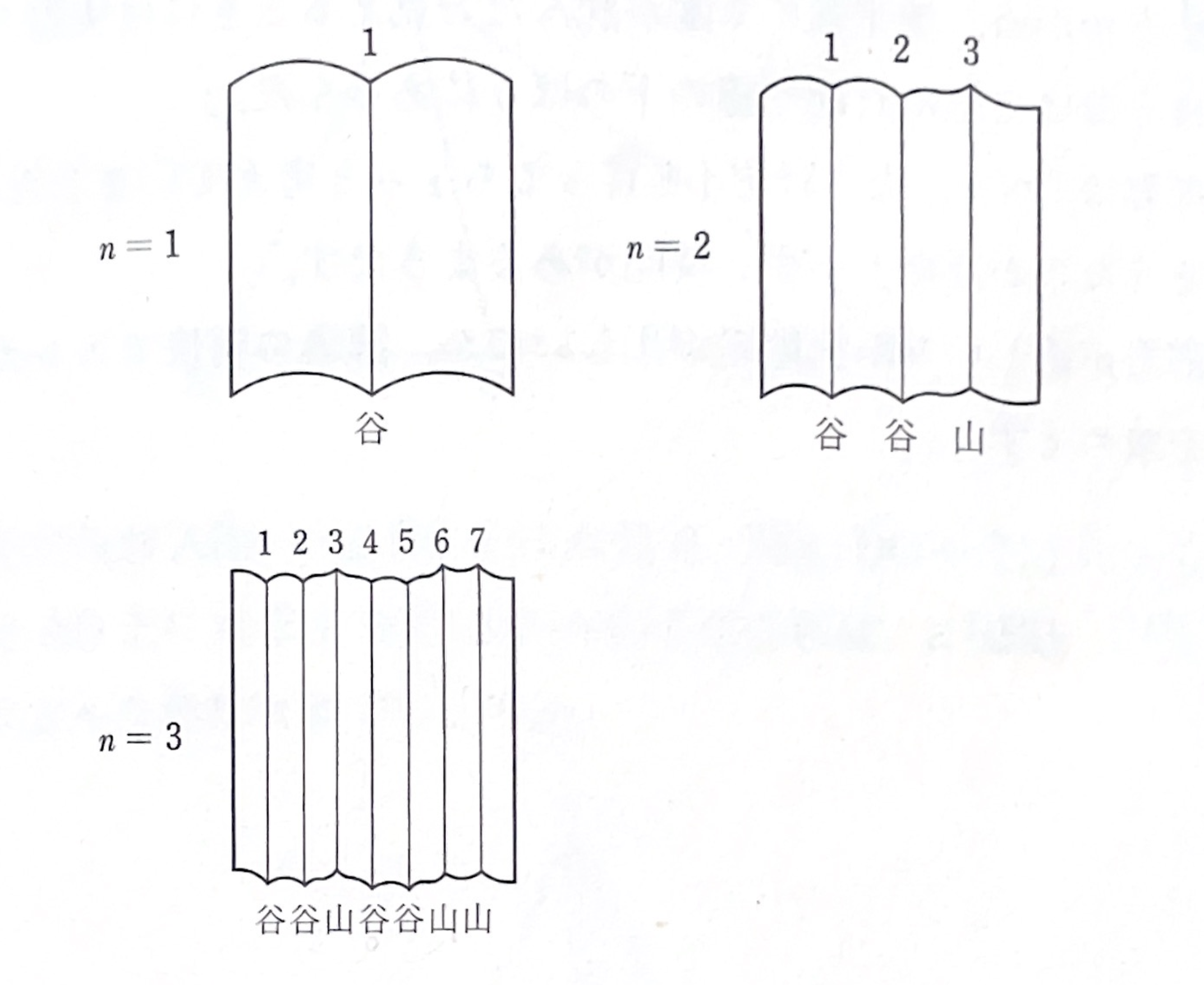
折り紙の左端を固定して、そこに右端が重なるように、手前に手前にと$n$回折りたたむ。それを開くと、$2^n-1$本の折り目ができていますが、左から数えて$m$番目の折り目が山折りなのか谷折りなのかを示すエレガントな公式を求めてください。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p11.

いざ、チャレンジ

チャレンジの結果、解けました！
割と簡単に感じました。

さて、では、筆者の解答を紹介します。

筆者の解答

まずは、$n=4$の場合を実際に折ってみました。
その結果、左から

となります。
この状態で

(ここ)の部分で半分にすると$n=3$の場合です。
そして、(ここ)の一つ右の隣の”谷”を堺にして山と谷が逆になっています。
さらに、一番左は谷で一番右は山です。
そして、真ん中は谷となっています。

要するに、$n$回折ったとき、真ん中の谷を堺にして左側は$n-1$回の折り目と同じ、ということです。
故に、$n-1$回折ったときの$m$番目は$n$回折ったときの$m$番目と同じ折り目になっています(ただし、$m\leq 2^{n-1}-1$)。
また、$n-1$回折ったときの$m$番目の折り目が、$n$回折ったときではその倍である$2m$番目の折り目にもなっています。
これは、1回折るごとに、折り目の数が倍になっていくからです(厳密に言うと、折り目と折り目の間に新しい折り目が増えるということです)。
ということは、新しい折り目というのは奇数番目の折り目、ということになります。

さらに、ここで$n=3$のときと$n=4$のときを見比べてみると、

です。
つまり、新しい折り目というのは左から谷と山を繰り返すのだ、ということが見えました。

以上のことをまとめれば、

• $m$が偶数番目のときは$\displaystyle\frac{m}{2}$と同じ折り目。
• $m$が奇数番目の折り目で、かつ$m$が奇数であれば、谷。
• $m$が偶数番目の折り目で、かつ$m$が偶数であれば、山。

ということが分かります。

解けたときには「よっしゃ！」と声がでました。
ちゃんと解けたのははじめてじゃないかな？

解答

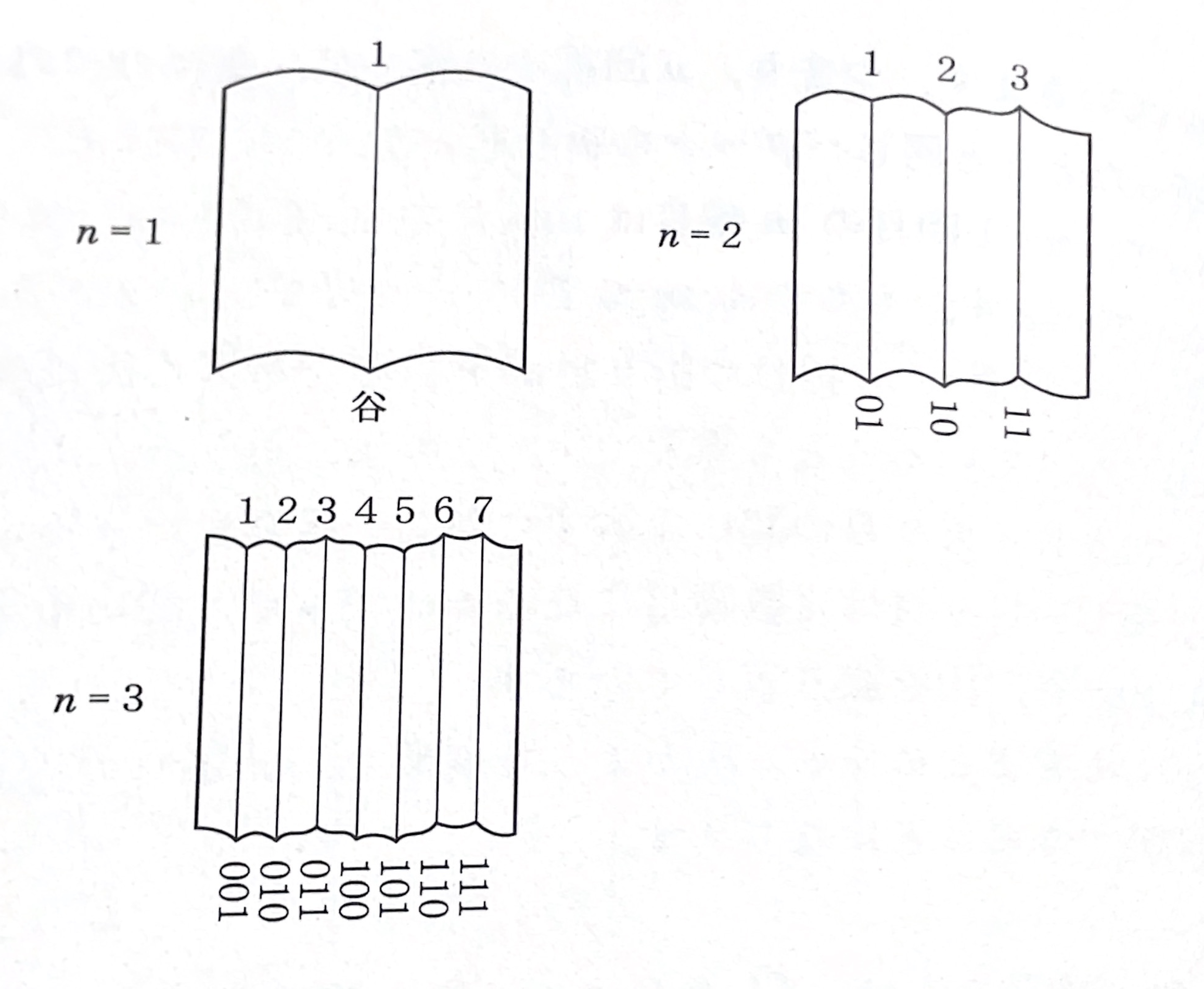
今回も偶然と解答が筆者とほぼ同じ部分があったので、それは省きますが、なんと、これを２進数でとらえる、というすごい解答がありました。

（前略）

$m$を2進数で表したときに、右から純に見ていって最初に現れる1の左隣が0ならば「谷折り」、1ならば「山折り」となります。

（中略）

1回目の折りたたみでは谷折りしか登場しないので、2回目から考えます。そのときにできる折り目は、左から、谷・谷・山となっています。一方、1,2,3を2桁の2進数で表すと順に01,10,11となり、今度の判定方法でもうまく判定できることが分かります。ただし、10は010だと思って下さい。
そこで、もう1回折ると、新たに001,011,101,111に対応した折り目ができて、古い折り目は010,100,110に対応します。この2進数は初めの2進数の末尾に0を追加したものになっています。
一般に、$n+1$回目に新たに生まれた折り目は、すでにできている折り目の間に1つずつ入るので、古い折り目($n$回目の$m$番目)は$2m$番目の折り目になります。2進数を2倍することは末尾に0を1つ追加することと同じなので(10進数を10倍するときと同じ原理です)、3回目の折りたたみで確認した現象と同様に、$n$回目の$m$番目の折り目は、$n+1$回目を折った後では$m$の2進数の末尾に0を追加して得られる番号に対応します。
また、新しい折り目は奇数番目になっていて、その奇数の2進数の末尾2桁に注目すると、01と11を交互に繰り返していて、01が谷折り、11が山折りに対応しています。
要するに、$m$の2進法表現のおしりに並ぶ0は、折り目のふるさに関係しているだけで、それが谷折りなのか、山折なのかには関係がありません。そして、右から見ていって最初に現れる1が、その折り目が誕生した瞬間に対応しています。その瞬間に、左から谷折りと山折が交互に誕生していきますが、それはちょうど最初に現れる1の次のくらいが0か1かに対応しています。

（後略）

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p71-p73.

これはすごいです。
全くその発想はありませんでした。
山、谷という状態を数で、しかも2進数で捉える、というのはまさにエレガントだと思います。

結

いかがでしたか？
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
魔法陣は初めて解きましたが、結局力技が入ってくるのでしょうか…?
時計の問題は結局筆者の読解力不足でした。

読者の皆様も是非一度挑戦してみて下さい！
そして、「こんな解答を思いついた！」というのがあれば是非コメントで教えて下さい！

質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

Twitterでもリプ、DM問わず質問、コメントを大募集しております！