「線型空間の基底と次元」【線型代数学の基礎シリーズ】線型空間編 その3

本記事の内容

本記事は「基底」および「次元」について解説する記事です。

本記事を読むにあたり、線型空間、線型独立について知っている必要があるため、以下の記事も合わせてご覧ください。

↓線型空間の記事

「線型空間、線型結合、部分空間」【線型代数学の基礎シリーズ】線型空間編 その1

...

for-spring.com

2022.07.11

↓線型独立の記事

「線型独立、線型従属とその基本的な性質」【線型代数学の基礎シリーズ】線型空間編 その2

...

for-spring.com

2022.07.12

本記事を読む前にちょっとだけ言いたいこと(本質的に内容には関係ありませんので、読み飛ばしてOKです)

線型空間の単元は特に「以前証明したことを使って新たな事実を導く」という操作が多い気がします。
そういう意味で、「あれ？これ何だっけ？」となることが多くなると思います。
線型空間の難しさはその抽象性にあると思いますが、その一方で以前に証明した事実をたくさん使うということで混乱しやすいということもまた難しさだと思います。

要するに何が言いたいかというと、ちょこちょこ復習しながら、つまり「そういやそうだったよね」と思い出しながら学んでいくのがいいと思います。

おしまい

※今回は紹介する定理が多いため、証明をコンパクトにまとめてみました。
「いや、分かりにくいわ」という方は是非「分かりにくい」というコメントをいただけると嬉しいです。その際は後日この記事を更新してより丁寧な証明を掲載します。

基底

以前の記事で「基底は線型空間の風貌を知るために重要だ」という主旨の話をしました。
それは「基底は線型空間における座標軸的な役割を担っているから」でした。
この話については後述します。

基底を学ぶ前にちょっと考えてみる

実は、すでに基底という言葉は本ブログで出てきています。
というのも、標準基底というベクトルの話をすでにしているからです。

$\mathbb{R}^n$の標準基底とは何だったか、というと
$$\boldsymbol{e}_1= \left( \begin{array}{c} 1\\ 0\\ \vdots \\ \vdots \\ 0 \end{array} \right),\quad \boldsymbol{e}_2= \left( \begin{array}{c} 0\\ 1\\ 0 \\ \vdots \\ 0 \end{array} \right),\cdots, \boldsymbol{e}_n= \left( \begin{array}{c} 0\\ \vdots\\ \vdots \\ 0 \\ 1 \end{array} \right)$$
でした。

特に、三次元の場合、すなわち$\mathbb{R}^3$の場合は
$$\boldsymbol{e}_1= \left( \begin{array}{c} 1\\ 0\\ 0 \end{array} \right),\quad \boldsymbol{e}_2= \left( \begin{array}{c} 0\\ 1\\ 0 \\ \end{array} \right),\quad \boldsymbol{e}_3= \left( \begin{array}{c} 0\\ 0 \\ 1 \end{array} \right)$$
でした。

これを図示すると、以下です。

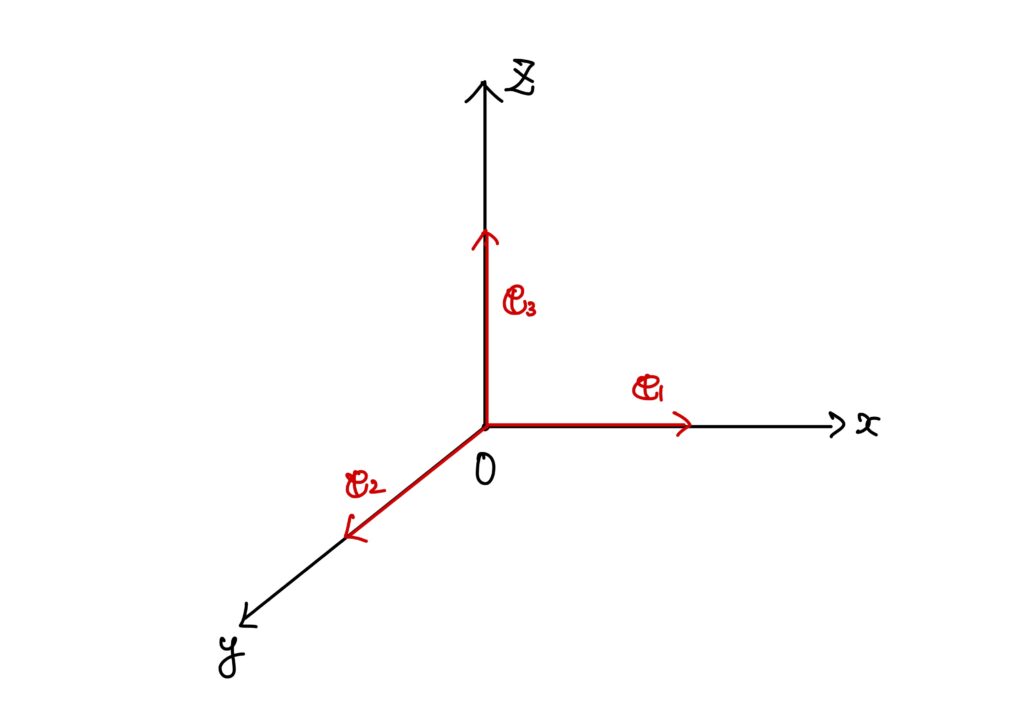
つまり、それぞれ座標軸上の単位ベクトルを表しています。

線型空間$\mathbb{R}^3$の任意のベクトル$\boldsymbol{x}$を
$$\left( \begin{array}{c} x_1\\ x_2 \\ x_3 \end{array} \right)$$
と書いたとすると、
$$\begin{eqnarray} \boldsymbol{x}= \left( \begin{array}{c} x_1\\ x_2 \\ x_3 \end{array} \right)&=& \left( \begin{array}{c} x_1\\ 0\\ 0 \end{array} \right)+ \left( \begin{array}{c} 0\\ x_2\\ 0 \\ \end{array} \right)+ \left( \begin{array}{c} 0\\ 0 \\ x_3 \end{array} \right)\\ &=&x_1\left( \begin{array}{c} 1\\ 0\\ 0 \end{array} \right)+ x_2\left( \begin{array}{c} 0\\ 1\\ 0 \\ \end{array} \right)+ x_3\left( \begin{array}{c} 0\\ 0 \\ 1 \end{array} \right)\\ &=& x_1\boldsymbol{e}_1+x_2\boldsymbol{e}_2+x_3\boldsymbol{e}_3 \end{eqnarray}$$

と書けます。
さらに、$\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3$は線型独立です。
ここで、以下の事実を思い出します。

この定理1.の証明は【線型代数学の基礎シリーズ】線型空間編 その2を御覧ください。

つまり、$\boldsymbol{x}$の表し方
$$\boldsymbol{x}=x_1\boldsymbol{e}_1+x_2\boldsymbol{e}_2+x_3\boldsymbol{e}_3$$
は一意的です。

故に、標準基底は座標軸的な役割を担っています。

基底を一言で

基底を一言でいうと、ある種の座標軸、ということなのですが、もうちょっとしっかり書くと次です。

です。
「”生成する”ってどういうことだっけ？」となった方もいらっしゃると思いますが、後で復習することにして、基底を数学的に明示します。

基底を数学的に

ここで、「”生成する”」ということについて復習します。

この定理2.の証明は【線型代数学の基礎シリーズ】線型空間編 その1を御覧ください。

この定理2.によって保証されている部分空間$W$を$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$によって生成される部分空間というのでした。
つまり、基底というのは、線型独立であって、かつ
$$V=\left\{x_1\boldsymbol{a}_1+x_2\boldsymbol{a}_2+\dots+x_n\boldsymbol{a}_n \middle| x_i\in\mathbb{R},\ i=1,2,\dots,n\right\}$$
となるときを言うわけです。

ここで、注意なのですが、線型空間$V$に対して基底の取り方は1通りではありません。
いっぱいあります。

こんなのも基底です。

簡単ですが例を挙げましょう。
線型空間$\mathbb{R}^3$において標準基底$\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3$は基底でした。

一方で、次のようにベクトル$\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3$を定めます。

例3.
$$\boldsymbol{a}_1=\left( \begin{array}{c} 1\\ 1 \\ 0 \end{array} \right),\quad \boldsymbol{a}_2=\left( \begin{array}{c} 0\\ 1 \\ 1 \end{array} \right),\quad \boldsymbol{a}_1=\left( \begin{array}{c} 1\\ 0 \\ 1 \end{array} \right)$$
は基底です。

これを示すには

• $\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3$が線型独立であること。
• $\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3$が$\mathbb{R}^3$を生成すること。

を確かめる必要があります。

前者については簡単なのでちょいちょい省略しながら説明します。
$$c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+c_3\boldsymbol{a}_3=\boldsymbol{0}$$
としたとき、$c_1=c_2=c_3=0$であれば$\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3$は線型独立です。
これを示すためには以下の連立一次方程式を解けばOKです。

$$\begin{cases} c_1+c_3=0\\ c_1+c_2=0\\ c_2+c_3=0 \end{cases}$$

これを解くと、$c_1=c_2=c_3=0$が導けます。
故に、$\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3$は線型独立です。

次に$\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3$が$\mathbb{R}^3$を生成するか、という話ですが、これも大したことはありません。

つまり、知りたいのは、任意のベクトル$\boldsymbol{b}\in \mathbb{R}^3$に対して、
$$\boldsymbol{b}=\left( \begin{array}{c} b_1\\ b_2 \\ b_3 \end{array} \right)$$
と書いたとき、等式
$$c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+c_3\boldsymbol{a}_3=\boldsymbol{b}$$
を満たすような$c_1,c_2,c_3$が存在するか？ということです。
これは以下の連立一次方程式に解があるのか？ということになります。

$$\begin{cases} c_1+c_3=b_1\\ c_1+c_2=b_2\\ c_2+c_3=b_3 \end{cases}$$
この連立一次方程式を行列で表現すると、
$$\begin{pmatrix} 1&0&1\\ 1&1&0\\ 0&1&1 \end{pmatrix} \left( \begin{array}{c} c_1\\ c_2\\ c_3\end{array} \right)= \left( \begin{array}{c} b_1\\ b_2\\ b_3\end{array} \right)$$
です。
このとき、
$$\left| \begin{array}{c} 1&0&1\\ 1&1&0\\ 0&1&1 \end{array} \right|=1+1=2$$
となってこの行列には逆行列が存在します。
実際計算してみると、逆行列は
$$\begin{pmatrix} 1&0&1\\ 1&1&0\\ 0&1&1 \end{pmatrix}^{-1}= \begin{pmatrix} \displaystyle\frac{1}{2}&\displaystyle\frac{1}{2}&\displaystyle-\frac{1}{2}\\ \displaystyle-\frac{1}{2}&\displaystyle\frac{1}{2}&\displaystyle\frac{1}{2}\\ \displaystyle\frac{1}{2}&\displaystyle-\frac{1}{2}&\displaystyle\frac{1}{2} \end{pmatrix}$$
となります。
従って、
$$\begin{eqnarray} \left( \begin{array}{c} c_1\\ c_2\\ c_3\end{array} \right)&=& \begin{pmatrix} \displaystyle\frac{1}{2}&\displaystyle\frac{1}{2}&\displaystyle-\frac{1}{2}\\ \displaystyle-\frac{1}{2}&\displaystyle\frac{1}{2}&\displaystyle\frac{1}{2}\\ \displaystyle\frac{1}{2}&\displaystyle-\frac{1}{2}&\displaystyle\frac{1}{2} \end{pmatrix} \left( \begin{array}{c} b_1\\ b_2\\ b_3\end{array} \right)\\ &=& \left( \begin{array}{c} \displaystyle\frac{1}{2}b_1+\frac{1}{2}b_2-\frac{1}{2}b_3\\ \displaystyle-\frac{1}{2}b_1+\frac{1}{2}b_2+\frac{1}{2}b_3\\ \displaystyle\frac{1}{2}b_1-\frac{1}{2}b_2+\frac{1}{2}b_3 \end{array} \right) \end{eqnarray}$$
となるので、$c_1,c_2,c_3$が存在します。

以上のことから$\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3$は基底です。

線型空間の次元を語る上での準備(行列式と線型独立の関係)

いくつか行列式と線型独立の関係を表す定理を証明します。

定理4.の証明

(1.$\Rightarrow$2.の証明)

$\det(A)\neq0$であれば、$A$の逆行列$A^{-1}$が存在します。
従って、連立一次方程式$A\boldsymbol{x}=\boldsymbol{0}$はの解$\boldsymbol{x}$は
$$A^{-1}A\boldsymbol{x}=A^{-1}\boldsymbol{0} \Leftrightarrow \boldsymbol{x}=\boldsymbol{0}$$
です。
ここで、$A\boldsymbol{x}=\boldsymbol{0}$は
$$\boldsymbol{x}= \left( \begin{array}{c} x_1\\ \vdots\\ x_n \end{array} \right)$$
と書いたとすると、
$$x_1\boldsymbol{a}_1^\prime+x_2\boldsymbol{a}_2^\prime+\dots+x_n\boldsymbol{x}_n=\boldsymbol{0}$$
と書かれるから、この式を満たす$\boldsymbol{x}$が零ベクトルに限る、ということになります。
従って、これはまさに列ベクトル$\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\dots,\boldsymbol{a}^\prime_n$は線型独立です。

(2.$\Rightarrow$1.の証明)

対偶を示します。
$\det(A)=0$とすると、$A$には逆行列が存在しません。
従って、連立一次方程式$A\boldsymbol{x}=\boldsymbol{0}$は$\boldsymbol{x}=\boldsymbol{0}$以外の解を持つことになります。
すなわち、
$$\boldsymbol{x}= \left( \begin{array}{c} x_1\\ \vdots\\ x_n \end{array} \right)$$
と書いたとき、
$$x_1\boldsymbol{a}_1^\prime+x_2\boldsymbol{a}_2^\prime+\dots+x_n\boldsymbol{x}_n=\boldsymbol{0}$$
を満たす$x_1,\dots,x_n$の中で少なくとも１つが$0$でないわけです。
これはまさに列ベクトル$\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\dots,\boldsymbol{a}^\prime_n$が線型従属であることを示しています。

(1.$\Rightarrow$3.の証明)

$\det(A^\top)=\det(A)$ですので、今の議論を$A^\top$に直せばOKです。

定理4.の証明終わり

定理5.の証明

$n+1$個の$n$項数ベクトルを$\boldsymbol{a}_i=(a_{i1}\ \cdots\ a_{in})\ (i=1,\dots,n+1)$とします。
このとき、
$$\left| \begin{array}{c} a_{11}&a_{12}&\cdots &a_{1n}&0\\ a_{21}&a_{22}&\cdots &a_{2n}&0\\ \vdots&\vdots& \ddots&\vdots&\vdots\\ a_{n+1\ 1}&a_{n+1\ 2}&\cdots &a_{n+1\ n}&0\\ \end{array} \right|=0$$
ですので、
定理4.から
$$(a_{11}\ \cdots\ a_{1n}\ 0),\dots,(a_{n+1\ 1}\ \cdots\ a_{n+1\ n}\ 0)$$
は線型従属です。
従って、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_{n+1}$も線型従属です。

定理5.の証明終わり

定理6.の証明

これは次の定理が成り立ってるので、特別な場合にのみ証明すればOKです。

定理7.の証明は【線型代数学の基礎シリーズ】線型空間編 その2を御覧ください。

定理7.により$s=r+1$の場合に証明すればOKです。
仮定から、
$$\boldsymbol{b}_j=\sum_{i=1}^rc_{ij}\boldsymbol{a}_i\quad (j=1,2,\dots,r+1)$$
と書かれます。
このとき$C=\left( c_{ij}\right)$とすると、$C$は$(r,r+1)$型の行列で、かつ
$$(\boldsymbol{b}_1\ \cdots\ \boldsymbol{b}_{r+1})=(\boldsymbol{a}_1\ \cdots\ \boldsymbol{a}_r)C$$
と書くことができます。
$C$の転置行列$C^\top$は$(r+1,r)$型の行列なので、定理5.から$C^\top$の$r+1$個の行ベクトルは線型従属です。

故に、
$$\sum_{j=1}^{r+1}d_jc_{ij}=0$$
がすべての$i=1,\dots,r$に対して$d_1,\dots,d_{r+1}$で、この中の少なくとも１つが$0$でないものが存在します。
ここで、
$$\boldsymbol{d}= \left( \begin{array}{c} d_1\\ \vdots\\ d_{r+1} \end{array} \right)$$
とすると、$\boldsymbol{d}$は$\boldsymbol{0}$ではないベクトルで、上の式は
$$C\boldsymbol{d}=\boldsymbol{0}$$
と書き表されます。
ただし、$\boldsymbol{0}$は$r$次元の零ベクトルです。
そこで、次の線型結合を考えてみます。

$$\begin{eqnarray} d_1\boldsymbol{b}_1+\dots+d_{r+1}\boldsymbol{b}_{r+1}&=& (\boldsymbol{b}_1\ \cdots \boldsymbol{b}_{r+1})\boldsymbol{d}\\ &=&(\boldsymbol{a}_1\ \cdots\ \boldsymbol{a}_r)C\boldsymbol{d}\\ &=&(\boldsymbol{a}_1\ \cdots\ \boldsymbol{a}_r)\boldsymbol{0}=\boldsymbol{0} \end{eqnarray}$$
が成り立ちます。
しかも$d_i$のうち、少なくとも１つが$0$でないわけですので、これはまさに$\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_{r+1}$は線型従属です。

定理6.の証明終わり

いやあ、長かったですねえ。
ちょいと面倒でしたが、線型空間の次元のお話をするにあたって必要なので書きました。

要するに、この章で言いたかったのは、行列式と線型独立には関係があって、線型独立か否かということが行列式を計算することで分かり、そして余分なベクトルがあればそれらは線型従属だということです。

線型空間の次元

筆者は”次元”と言われると「大介？」と思いますが、そんなことは置いておいて、線型空間には次元というものがあります。

$\mathbb{R}^n$の場合の次元は簡単で、$n$です。
しかし、線型空間は必ずしも$\mathbb{R}^n$の形をしているわけではありません。
一般の線型空間の次元について語るために少々準備します。

「おいおいおい…まーだ準備することがあんのかよお…」と思うかもしれません。
そうですね。
筆者も書いていて思います。
でも、同時に「ああ、やっぱり数学って緻密に議論が建てられているんだなあ」とも思います。
とはいっても、読む側、書く側、双方ともに大変なのはその通りですよね。

さて、気合を入れ直して準備に取り掛かりましょう。

線型空間の次元のための準備

何個か事実を証明します。

定理8.の証明

なんてことありません。

仮定から$\boldsymbol{a}_i$は$\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_s$の線型結合で表すことができて、かつ$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$が線型独立なので、定理6.の対偶から$r\leq s$です。
同様にして、各$\boldsymbol{b}_j$が$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$の線型結合で表されて、かつ$\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_s$が線型独立であるから、$r\geq s$です。
すなわち、$r=s$です。

定理8.の証明終わり

つまり、「どんな基底の取り方をしたとしても、基底を構成するベクトルの個数は変わりませんよ」ということです。

先程の事実を使えば一瞬で終わります。

定理9.の証明

$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$と$\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_s$を線型空間$V$の2つの基底だとします。

このとき、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$と$\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_s$はそれぞれ線型独立で、かつ$V$を生成します。
すなわち、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$は$V$を生成して、かつ$\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_s$も$V$を生成して、そして$V\subset V$ですので、$V$は$V$の部分空間ですから定理8.が使えます。
故に、定理8.から$r=s$となって証明完了です。

定理9.の証明終わり

定理9.を少しだけ言い換えると、要するに線型空間$V$に対して、その基底の取り方はいくらでもあるのですが、基底を構成するベクトルの個数はあくまで$V$に依存する、すなわり$V$によって定まる、ということです。
実はこのことが次元のコンセプトです。

で、線型空間の次元って？

この章の導入で「$\mathbb{R}^n$の次元は$n$ですよ〜」という話をしましたが、なぜかというと$\mathbb{R}^n$の標準基底$\boldsymbol{e}_1,\dots,\boldsymbol{e}_n$が$n$個のベクトルだからです。

余談

一般の線型空間$V$では、基底を構成するベクトルの個数が必ずしも有限だとは限りません。
無限の場合、無限次元の線型空間といいます。
また、基底を構成するベクトルの個数が有限のときは有限次元の線型空間といいます。
有限このベクトルで生成される線型空間は有限次元です。
一般に線型空間の次元が自然数として定まるのはこの有限生成の線型空間の場合です。

線型空間の次元の基本的な性質

定理10.の証明終わり

$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$を$V$の１つの基底とします。
$V$から任意に$r$個$(r\geq n+1)$のベクトル$\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_r$をとると、これらは$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$の線型結合で表すことができますので、定理6.から線型従属です。
すなわち、$n+1$個以上の$V$の任意のベクトルの組は常に線型従属です。
一方で、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$は線型独立ですので、$V$に含まれる線型独立なベクトルの最大個数はちょうど$n$個です。

定理10.の証明終わり

基底の条件

基底たりえる条件について解説します。
要するに必要十分条件です。

定理11.の証明

(1.$\Rightarrow$2.の証明)

線型空間$V$の１つの基底を$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$とします。
$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$は基底ですので、$V$を生成します。
従って、任意の$V$のベクトル$\boldsymbol{a}$はこれらの線型結合で表すことができ、さらにこれらは線型独立です。
ここで、定理1.から線型結合の表し方は一意的です。

(2.$\Rightarrow$1.の証明)

仮定から、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$は$V$を生成して、線型結合の表し方が一意的ですので、これも定理1.により$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$は線型独立です。
故に、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$は$V$の基底となるので、$\dim V=n$です。

定理11.の証明終わり

さて、本記事の目玉と言ってもいい事実を証明します。

定理12.の証明

そもそも、2.と3.を満たすベクトルが基底なので、1.$\Rightarrow$2.、3.が成り立ちます。
従って、2.$\Rightarrow$1.と3.$\Rightarrow$1.を証明すればOKです。

(2.$\Rightarrow$1.の証明)

$\boldsymbol{a}$を$V$の任意のベクトルとします。
$n+1$個の$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n,\boldsymbol{a}$を考えると、今$\dim V=n$なので、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n\,\boldsymbol{a}$は線型従属です。
ここで、次の事実を使います。

定理13.の証明は【線型代数学の基礎シリーズ】線型空間編 その2を御覧ください。

従って、定理13.により$\boldsymbol{a}$は$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$の線型結合で書くことができます。
これはまさに、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$が$V$を生成しているということですので、$V$の基底です。

(3.$\Rightarrow$1.の証明)

$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$の中の線型独立なベクトルの最大個数を$r$個とします。
例えば、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$が線型独立だとします。
今、$r<n$として矛盾を導きます(背理法)。

$r<s\leq n$を満たす任意の$s$に対して、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r,\boldsymbol{a}_s$は線型従属ですので、再度定理13.を使うことで、$\boldsymbol{a}_s$は$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$の線型結合で書くことができます。
故に、$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$は$V$を生成するため、$V$の基底となります。
しかしながら、これは$\dim V=n$に矛盾しますので、$r=n$です。
以上のことから$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$は$V$の基底となって、1.が成り立ちます。

定理12.の証明終わり

結

今回は、基底、線型空間の次元について解説しました。
最も言いたかったことは、定理12.です。
つまり、線型空間の次元と同じ数だけ線型独立なベクトルを取ってくれば、是則基底だ、ということになります。

基底というのはある種の座標軸的な役割がありますので、与えられた線型空間の要素の風貌を捉えるのに誠に有用です。

次回はランクについて解説します。

乞うご期待！質問、コメントなどお待ちしております！