本記事の内容
本記事は行列のランクについて解説する記事です。
本記事を読むにあたり、線型空間、および線型写像について知っている必要があるため、以下の記事も合わせてご覧ください。
↓線型空間の記事
↓線型写像の記事
本記事を読む前に
今回のランクの話は、主な対象が行列ですので、”行列編”ということになっていますが、線型空間の話、特に線型空間の次元の話を知っている必要があります。
そういう意味では、【線型代数学の基礎シリーズ】線型空間編 その3をご覧いただいた後に、読んでいただきたい記事となっています。
線型写像の厳密な話
以前の記事で、線型写像について説明しましたが、それはあくまで\(\mathbb{R}^m\)から\(\mathbb{R}^n\)への線型写像の話でした。
実は、線型写像というのは一般の線型空間から線型空間への写像として定められます。
\(\mathbb{R}^m\)および\(\mathbb{R}^n\)は線型空間の最たる例だった、という話です。
では、一般の線型空間における線型写像を説明します。
とか言っときながら、実は本当の意味で一般の線型写像を定めるには体(たい、英:field)という代数系について知っている必要があります。
しかし、本ブログでは(今の所)体については述べないので、\(\mathbb{R}\)上の線型空間における線型写像について解説します。
\(\mathbb{R}\)上の線型空間に対する線型写像
線型写像
\(V\)および\(W\)を\(\mathbb{R}\)上の線型空間とする。\(V\)から\(W\)への写像\(f:V \to W\)が線型写像(a linear map)であるとは、次の1.および2.を満たすときを言う。- \(f(\boldsymbol{x}+\boldsymbol{y})=f(\boldsymbol{x})+f(\boldsymbol{y})\quad(\boldsymbol{x},\boldsymbol{y}\in X)\)
- \(f(\lambda\boldsymbol{x})=\lambda f(\boldsymbol{x})\quad(\lambda\in\mathbb{R},\boldsymbol{x}\in V)\)
以前の記事でも述べましたが、線型写像が満たすべき2条件の等式の左辺の\(+\)と右辺の\(+\)は違います。
スカラー倍についても同じです。
これについての説明は【線型代数学の基礎シリーズ】行列編 その5を御覧ください。
像空間と核空間
線型写像の像と核(後で説明します)について、学んでおきましょう。
線型写像は写像なので、像を考えることができます。
線型写像の像は線型空間になっていて、より詳しく言うと、
ということです。
像空間と核空間
\(V\)、\(W\)を線型空間、\(f:V \to W\)を線型写像とする。このとき $$ f(V)={\rm Image}(f)={\rm Im}(f)=\left\{f(\boldsymbol{x})\middle| \boldsymbol{x}\in V\right\} $$ を\(f\)の像空間という。また、 $$ {\rm Ker}(f)=\left\{\boldsymbol{x}\in V\middle|f(\boldsymbol{x})=\boldsymbol{0}\right\} $$ を\(f\)の核空間という。要するに、核空間というのは、線型写像によって線型空間の和の単位元に対応するような定義域の要素のことを指します。
先に述べたとおり、像空間と核空間はそれぞれ線型空間です。
つまり、以下が成り立ちます。
定理1.
\(f\)を線型空間\(V\)から\(W\)への線型写像とする。このとき、以下が成り立つ。- \(f\)の像空間\({\rm Image}(f)\)は\(W\)の部分空間である。
- \(f\)の核空間\({\rm Ker}(f)\)は\(V\)の部分空間である。
定理1.の証明
この定理を証明するにあたって、すなわち部分空間であるということを証明するにあたって、以下の事実を使います。
定理2.(部分空間の必要十分条件)
線型空間\(V\)の部分集合\(W\)が部分空間であるための必要十分条件は次の3条件が成り立つことである。- \(W\neq \emptyset\quad\)(\(\emptyset\)は空集合)
- 任意の\(\boldsymbol{a},\boldsymbol{b}\in W\)および任意の\(c,d\in\mathbb{R}\)に対して、\(c\boldsymbol{a}+d\boldsymbol{b}\in W\)
この定理2.の証明は【線型代数学の基礎シリーズ】線型空間編 その1を御覧ください。
(1.の証明)
\(V\)は線型空間なので\(\boldsymbol{0}\in V\)です。
さらに、\(f\)は線型写像なので、任意の\(\boldsymbol{x},\boldsymbol{y}\in V\)に対して、\(f(\boldsymbol{x}+\boldsymbol{y})=f(\boldsymbol{x})+f(\boldsymbol{y})\)が成り立つので、\(\boldsymbol{x}=\boldsymbol{y}=\boldsymbol{0}\)としてもOKです。
従って、
$$
f(\boldsymbol{0}+\boldsymbol{0})=f(\boldsymbol{0})=\boldsymbol{0}\in{\rm Image}(f)
$$
となり、\({\rm Image}(f)\)は空集合ではありません。
また、任意の\(\lambda,\mu\in\mathbb{R}\)と任意の\(f(\boldsymbol{x}),f(\boldsymbol{y})\in{\rm Image}(f)\)に対して、\(f\)が線型写像だから
$$
\lambda f(\boldsymbol{x})+\mu f(\boldsymbol{y})=f\left(\lambda\boldsymbol{x}+\mu\boldsymbol{y}\right)\in{\rm Image}(f)
$$
となるので、\({\rm Image}(f)\)は\(W\)の部分空間です。
(2.の証明)
\(f\)は線型写像ですので、1.と同様に\(f(\boldsymbol{0})=\boldsymbol{0}\)ですから、\(0\in{\rm Ker}(f)\)です。
従って、\({\rm Ker}(f)\neq\emptyset\)です。
また、任意の\(\lambda,\mu\in\mathbb{R}\)と任意の\(\boldsymbol{x},\boldsymbol{y}\in{\rm Ker}(f)\)に対して、\(f\)が線型写像だから
$$
f\left(\lambda\boldsymbol{x}+\mu\boldsymbol{y}\right)=\lambda f(\boldsymbol{x})+\mu f(\boldsymbol{y})=\lambda\boldsymbol{0}+\mu\boldsymbol{0}
$$
となって\(\lambda\boldsymbol{x}+\mu\boldsymbol{y}\in{\rm Ker}(f)\)となるので、\({\rm Ker}(f)\)は\(V\)の部分空間です。
定理1.の証明終わり
行列のランク①(像空間からのアプローチ)
行列のランクというのは一見シンプルですが、ランクが持つ情報量は実は多かったりします。
ランクを一言で
ランクを一言でいうと、
です。
「そんなんに何の意味があるんだ?」と思うかもしれませんが、実はランクの数と線型空間の次元が関わっていたりするんですね。
前回の記事で線型空間の次元について解説しましたが、「じゃあどうやって求めんのよ?」というところまでは踏み込んでませんでした。
実はこのランクが次元とか変わっているおかげで線型空間の次元を把握しやすくなります。
ランクの定め方は色々あるんですが、個人的に「写像の言葉で書かれていてわかりやすいなあ」と思うものを説明します。
で、ランクって何よ?(ランクの定め方①)
ランク
\(m,n\in\mathbb{N}\)、\(A=\left( a_{ij}\right)\)を\((m,n)\)型の行列とする。このとき、\(A\)が定める線型写像 $$ A:\mathbb{R}^n\to\mathbb{R}^m $$ の像空間\({\rm Image}(A)\)の次元のことを\(A\)のランク(rank)、あるいは階数といい、\({\rm rank}(A)\)で表す。すなわち、 $$ {\rm rank}(A)=\dim\left( {\rm Image}(A)\right) $$ である。【線型代数学の基礎シリーズ】行列編 その5で述べたとおり、行列は線型写像で表現でき、逆に線型写像も行列で表現できるのでした。
「これがどうして行列の階段の数と対応するんだ?」と思うかもしれませんが、その説明については次回解説します。
ランクのちょっとした性質
ランクのちょっとした性質をお話します。
定理3.
\(m,n\in\mathbb{N}\)、\(A=\left( a_{ij}\right)\)を\((m,n)\)型の行列とし、\(\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\dots,\boldsymbol{a}_n^\prime\)を\(A\)の列ベクトルとする。このとき、 $$ {\rm rank}(A)=\dim\left( S[\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\dots,\boldsymbol{a}_n^\prime]\right) $$ である。これがランクと線型空間の次元の関係性をあらわしている事実の1つです。
定理3.の証明
\(\mathbb{R}^n\)の任意のベクトル\(\boldsymbol{x}\)を\(\displaystyle\boldsymbol{x}=\left(\begin{array}{c}x_1\\ \vdots \\ x_n\end{array}\right)\)と書いたとします。
このとき、線型写像\(A\)による像\(A\boldsymbol{x}\)は
$$
A\boldsymbol{x}=x_1\boldsymbol{a}_1^\prime+\dots+x_n\boldsymbol{a}_n^\prime
$$
となるので、\({\rm Image}(A)=S[\boldsymbol{a}_1^\prime,\dots,\boldsymbol{a}_n^\prime]\)が成り立ちます。
従って、
$$
{\rm rank}(A)=\dim\left( {\rm Image}(A)\right)=\dim\left(S[\boldsymbol{a}_1^\prime,\dots,\boldsymbol{a}_n^\prime] \right)
$$
です。
定理3.の証明終わり
一旦計算してみっか
してみましょう。
例4.
$$
\begin{pmatrix}
1&-1&0\\
0&2&2\\
1&3&4
\end{pmatrix}
$$
のランクを計算してみます。
列ベクトルを順に\(\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\boldsymbol{a}_3^\prime\)とします。
このとき\(c_1\boldsymbol{a}_1^\prime+c_2\boldsymbol{a}_2^\prime+c_3\boldsymbol{a}_3^\prime=\boldsymbol{0}\)とすると、第2成分を比較して、\(c_2=0\)となり、\(c_1\boldsymbol{a}_1^\prime=\boldsymbol{0}\)において第1成分を見ることによって、\(c_1=0\)となります。
従って、\(\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime\)は線型独立です。
また、\(\boldsymbol{a}_3^\prime=\boldsymbol{a}_1^\prime+\boldsymbol{a}_2^\prime\)ですので、結局
$$
S[\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\boldsymbol{a}_3^\prime]=S[\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime]
$$
となり、\(\dim\left( S[\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\boldsymbol{a}_3^\prime]\right)=2\)です。
ランクは2です。
行列のランク②(小行列によるアプローチ)
ランクの定め方として、別の方法もあります。
それが小行列と呼ばれるものです。
小行列って?
小行列は「行列の一部からなる行列」のことです。
小行列
\(m,n\in\mathbb{N}\)とし、\(A=\left( a_{ij}\right)\)を\((m,n)\)型の行列とする。このとき、第\(i_1,i_2,\dots,i_r\)行\((i_1<i_2<\dots<i_r)\)と第\(j_1,j_2,\dots,j_s\)行\((j_1<j_2<\dots<j_s)\)の交わるところにある成分、すなわち \begin{eqnarray} && \begin{array}{c} &&\qquad\qquad j_1&&\quad\ j_2&\cdots&\ \ j_s&&\\ &&\qquad\qquad ↓&&\quad\ ↓&&\ \ ↓&&\\ \end{array}\\ && \begin{pmatrix} a_{11}&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&a_{1n}\\ &&\bigcirc&&\bigcirc&&\bigcirc&&\\ \vdots&&\bigcirc&&\bigcirc&&\bigcirc&&\vdots\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots\\ &&\bigcirc&&\bigcirc&&\bigcirc&&\\ a_{m1}&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&a_{mn}\\ \end{pmatrix} \begin{array}{c} \\ \leftarrow i_1行目\\ \leftarrow i_2行目\\ \vdots\\ \leftarrow i_r行目\\ \\ \end{array} \end{eqnarray} を取り出して作った\((r,s)\)型の行列 $$ \begin{pmatrix} a_{i_1j_1}&a_{i_1j_2}&\cdots &a_{i_1j_s}\\ a_{i_2i_1}&a_{i_2j_2}&\cdots &a_{i_2j_s}\\ \vdots&\vdots& \ddots&\vdots\\ a_{i_rj_1}&a_{i_rj_2}&\cdots &a_{i_rj_n}\\ \end{pmatrix} $$ を $$ A \left( \begin{array}{c} i_1&i_2&\cdots&i_r\\ j_1&j_2&\cdots&j_r\\ \end{array} \right) $$ で表し、\(A\)の小行列という。特に、\(r=s\)のとき、これを\(A\)の\(r\)次の小行列という。その時の行列式 $$ \left| A \left( \begin{array}{c} i_1&i_2&\cdots&i_r\\ j_1&j_2&\cdots&j_r\\ \end{array} \right) \right| $$ を\(A\)の\(r\)次の小行列式という。まさに、「行列の一部からなる行列」ということです。
この準備を元にして、ランクを別の定め方で表現してみます。
ランク(小行列によるランク)
行列\(A\)において、\(r\)次の小行列式の中には\(0\)でないものがあり、\(r+1\)以上の小行列式はすべて\(0\)であるとき、この\(r\)を\(A\)のランクといい、\({\rm rank}(A)\)で表す。ただし、零行列\(O\)のランクは\(0\)と定める。
ランクの考え方を理解する上で基本的な事実(証明は読み飛ばしてOK)
本当は、以前導入した像空間からのアプローチのランクと、小行列からのアプローチのランクとが一致することを証明する必要があるのですが、本ブログでは省きます。
(※「証明が欲しい!」という方はコメントを下さい。)
そして、この節で紹介する事実は証明が結構長くなってしまいますので、結果を認めて先に進んでいただいて結構です。
定理5.
\((m,n)\)型行列\(A\)の\(n\)個の列ベクトルが線型独立であるための必要十分条件は、\(A\)の\(n\)次の小行列式で値が\(0\)でないものが存在することである。定理5.の証明(読み飛ばしてOK)
①「列ベクトルが線型独立ならば小行列式が\(0\)でない小行列が存在する。」の証明
行列\(A=\left( a_{ij}\right)\)の\(n\)個の列ベクトルが線型独立だとします。
このとき、次の事実を使います。
定理6.
\(r<s\)とする。線型空間の\(s\)個のベクトル\(\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_s\)がすべて\(r\)個のベクトル\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)の線型結合で書かれれば、\(\boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_s\)は線型従属である。定理6.の証明は【線型代数学の基礎シリーズ】線型空間編 その3を御覧ください。
定理6. から\(m\geq n\)です。

今、\(A\)の行ベクトルの中から選ぶ事ができる線型独立なベクトルの最大個数を\(r\)とします。
すると、再度定理6.から\(r\leq n\)です。
\(r=n\)を示しましょう。
仮に、\(r<n\)として矛盾を導きます(背理法!)。
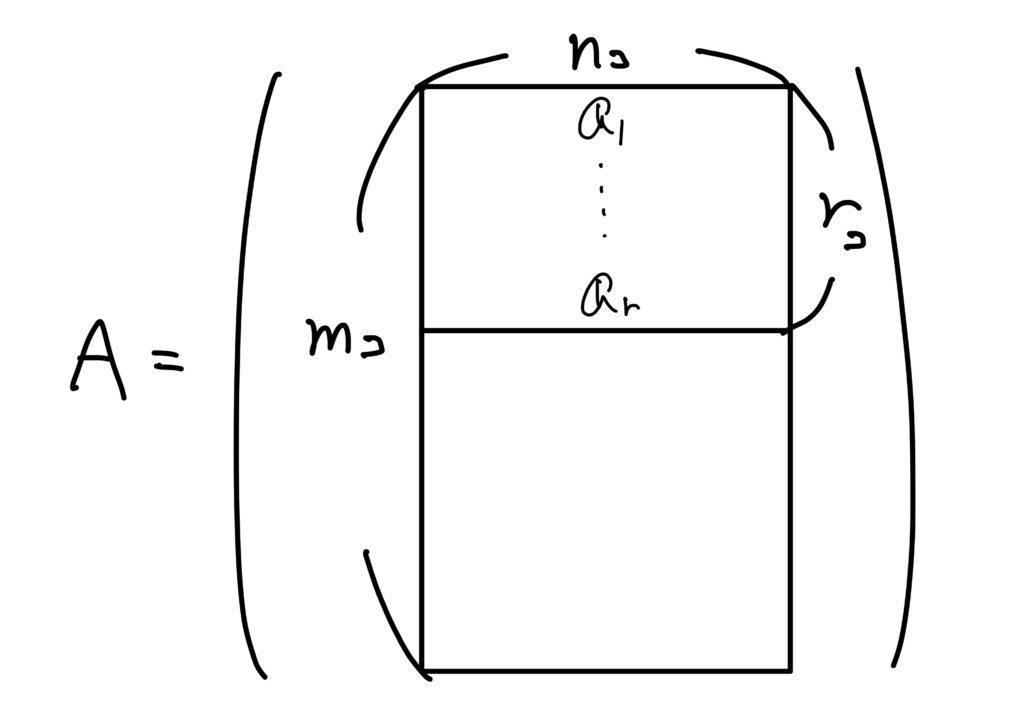
線型独立な行ベクトルの最大個数を与える行ベクトルを簡単のため、最初の\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_r\)とします。
このとき、\(r<s\leq m\)となるような任意の\(s\)に対して、\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_r,\boldsymbol{a}_s\)は線型従属です。
このとき、次の事実を使います。
定理7.
\(V\)を線型空間とする。\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)が線型独立で、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r,\boldsymbol{a}\)が線型従属であれば、\(\boldsymbol{a}\)は\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)の線型結合として一意的に表される。定理7.の証明は【線型代数学の基礎シリーズ】線型空間編 その2を御覧ください。
このとき、定理7.から\(\boldsymbol{a}_s\)は\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_r\)の線型結合で書くことができます。
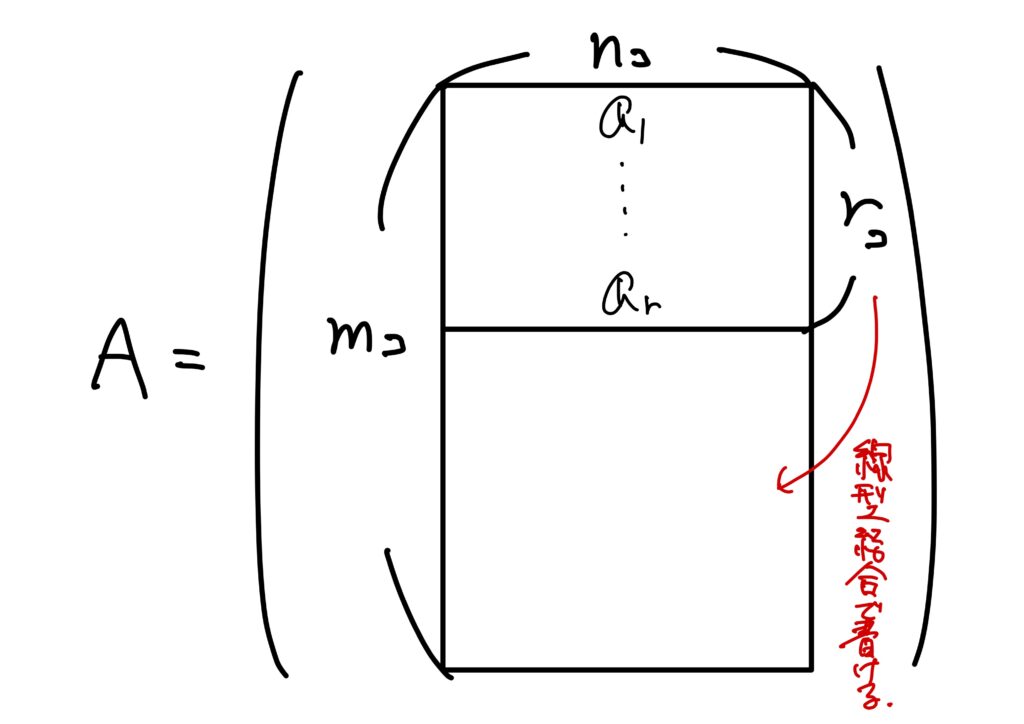
すなわち、
$$
\boldsymbol{a}_s=\sum_{i=1}^r\alpha_i\boldsymbol{a}_i\quad(r<s\leq m)
$$
です。
成分で言えば、
$$
a_{sj}=\sum_{i=1}^r\alpha_ia_{ij}
$$
が任意の\(1\leq j\leq n\)に対して成り立つ、ということです。
一方で、行列\(A=\left( a_{ij}\right)\)の列ベクトル\(\boldsymbol{a}_1^\prime,\dots,\boldsymbol{a}_r^\prime\)は項数が\(m\)個のベクトルですが、これから\(r+1\)番目以降の成分を取り除いて得られる項数が\(r\)個のベクトルを\(\boldsymbol{a}_1^{\prime r},\dots,\boldsymbol{a}_r^{\prime r}\)とします。
すなわち、
$$
\boldsymbol{a}_j^{\prime r}=
\left(\begin{array}{c}
a_{1j}\\
\vdots\\
a_{rj}
\end{array}
\right)\quad (1\leq j\leq n)
$$
です。
仮定から、\(r<n\)なのですから、再度定理6.からこれらは線型従属です。
すなわち、
$$
\sum_{j=1}^n\beta_j\boldsymbol{a}_j^{\prime r}=\boldsymbol{0}
$$
で、\(\beta_j\neq 0\)という\(1\leq j\leq n\)が存在するということになります。
この関係式を成分で書くと、
$$
\sum_{j=1}^n\beta_ja_{ij}=0
$$
が成り立つ、ということです。

この関係が\(r<s\leq m\)を満たす任意の\(s\)に対しても成り立つこと、すなわち、\(\sum_{j=1}^n\beta_ja_{sj}=0\)を示します。
\(r<s\leq m\)を満たす任意の\(s\)に対しては、先程示したように\(\displaystyle a_{sj}=\sum_{i=1}^r\alpha_ia_{ij}\)がすべての\(1\leq j\leq n\)に対して成り立っているので、
$$
\sum_{j=1}^n\beta_ja_{sj}=\sum_{j=1}^n\beta_j\left( \sum_{i=1}^r\alpha_ia_{ij}\right)=\sum_{i=1}^r\alpha_i\left( \sum_{j=1}^n\beta_ja{ij}\right)=\sum_{i=1}^r\alpha_i0=0
$$
となります。
これは、\(r<s\leq m\)を満たす任意の\(s\)に対してなりたつので、結局\(1\leq i\leq m\)を満たす任意の\(i\)に対して\(\displaystyle\sum_{j=1}^n\beta_ja_{ij}\)が成り立ちます。
故にベクトルの線型関係式
$$
\sum_{j=1}^n\beta_ja_{ij}=0
$$
が得られます。
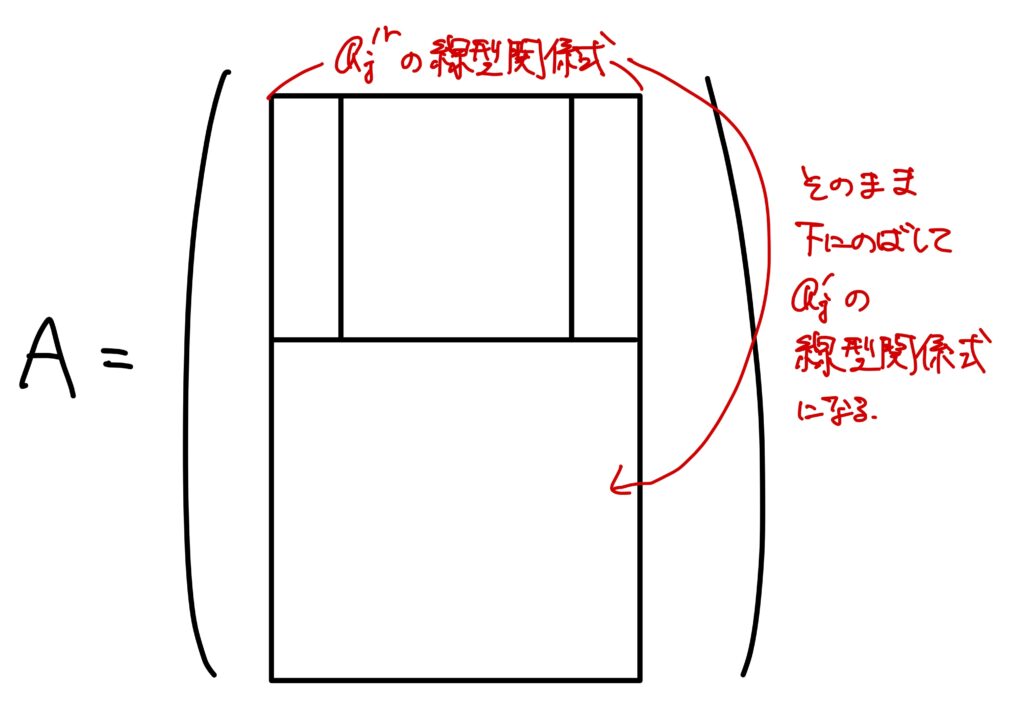
この線形関係式はある\(j\)で\(\beta_j\neq0\)だったので、\(\boldsymbol{a}_1^\prime,\dots,\boldsymbol{a}_n^\prime\)は線型従属です。
しかしながら、これは定理の仮定に矛盾です。
故に、\(r=n\)です。
この結果、項数が\(n\)個のベクトルである行のベクトル\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)が線型独立ということになり、これから作られる\(A\)の\(n\)次の小行列式
$$
\left|\begin{array}{c}\boldsymbol{a}_1\\ \vdots \\\boldsymbol{a}_n\end{array}\right|
=
\left|
\begin{array}{c}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{n1}&\cdots &a_{nn}\\
\end{array}
\right|
$$
は\(0\)ではありません。
実際、次の定理が成り立っていたからです。
定理8.
\(n\in\mathbb{N}\)とし、\(A\)を\(n\)次正方行列、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n\)を\(A\)の行ベクトル、\(\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\dots,\boldsymbol{a}_n^\prime\)を\(A\)の列ベクトル、とするとき、次の条件は同値である。- \(\det(A)\neq 0\)
- \(\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\dots,\boldsymbol{a}_n^\prime\)は線型独立である。
- \(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n\)は線型独立である。
定理8.の証明は【線型代数学の基礎シリーズ】線型空間編 その3を御覧ください。
②「小行列式が\(0\)でない小行列が存在するならば、列ベクトルが線型独立」の証明
逆に、\(A\)の小行列式で値が\(0\)でないものが存在したとします。
それらを最初の\(n\)行の行ベクトルからなる小行列式とします。
そのとき、\(A\)の各列ベクトルの後半の第\(n+1,\dots,\)第\(m\)成分を取り除いて得られる列ベクトル$$
\left(\begin{array}{c}
a_{11}\\
\vdots\\
a_{n1}
\end{array}
\right),\dots,
\left(\begin{array}{c}
a_{1n}\\
\vdots\\
a_{nn}
\end{array}
\right)
$$
は、再度定理8.から線型独立です。
従って、もともとの列ベクトル
$$
\left(\begin{array}{c}
a_{11}\\
\vdots\\
a_{n1}\\
\vdots\\
a_{m1}
\end{array}
\right),\dots,
\left(\begin{array}{c}
a_{1n}\\
\vdots\\
a_{nn}\\
\vdots\\
a_{mn}
\end{array}
\right)
$$
も線型独立です。
定理5.の証明終わり
ランクと同値なもの
最も言いたかったのがこれです。
定理9.
\((m,n)\)型行列\(A\)において、次の1.〜5.の数は一致する。- \(r={\rm rank}(A)\)
- \(A\)の列ベクトル(項数が\(m\)個のベクトル)の中から選びうる線型独立なベクトルの最大個数\(s\)
- 行列\(A\)の\(t\)次の小行列式の中には\(0\)でないものがあり、\(t+1\)次以上の小行列式はすべて\(0\)である。
- \(A\)の行ベクトル(項数が\(n\)個のベクトル)の中から選びうる線型独立なベクトルの最大個数\(u\)
- \(A\)の行ベクトルが生成する\(\mathbb{R}^n\)の部分空間の次元\(v\)
定理9.の証明
(1.\(\Leftrightarrow\)2.の証明)
一般に、\(S[\boldsymbol{a}_1^\prime,\dots,\boldsymbol{a}_n^\prime]\)の次元は\(\boldsymbol{a}_1^\prime,\dots,\boldsymbol{a}_n^\prime\)から選びうる線型独立なベクトルの最大個数に等しいので、定理3.から従います。
(2.\(\Leftrightarrow\)3.の証明)
線型独立な最大個数を与える\(A\)の列ベクトルを\(\boldsymbol{a}_{j1},\dots,\boldsymbol{a}_{js}\)とします。
この列ベクトルを並べてできる行列を\(A^\prime\)としましょう。
つまり、
$$
A^\prime=\left(\boldsymbol{a}_{j1}\ \dots\ \boldsymbol{a}_{js} \right)
$$
です。
\(A^\prime\)について定理5.を適用することによって、\(A^\prime\)の\(s\)次の小行列式でその値が\(0\)でないものが存在します。
\(A^\prime\)の小行列は、\(A\)の小行列だから、\(t\geq s\)が成り立ちます。
逆に、3.にある\(A\)の\(t\)次の小行列を
$$
A
\left(
\begin{array}{c}
i_1&i_2&\cdots&i_t\\
j_1&j_2&\cdots&j_t\\
\end{array}
\right)=
\begin{pmatrix}
a_{i_1j_1}&\cdots &a_{i_1j_n}\\
\vdots& \ddots&\vdots\\
a_{i_nj_1}&\cdots &a_{i_nj_n}\\
\end{pmatrix}
$$
とします。
すなわち、この小行列の行列式の値が\(0\)でなく、\(A\)の\(t+1\)次以上の任意の小行列式はすべて\(0\)だとすると、定理8.からこの小行列の列ベクトル
$$
\left(\begin{array}{c}
a_{i_1j_1}\\
\vdots\\
a_{i_tj_1}
\end{array}
\right),\dots,
\left(\begin{array}{c}
a_{i1j_t}\\
\vdots\\
a_{i_tj_t}
\end{array}
\right)
$$
は線型独立ですので、項数を増やした行列\(A\)の第\(j_1\)列、\(\cdots\)、第\(j_t\)列
$$
\left(\begin{array}{c}
a_{i_1j_1}\\
\vdots\\
a_{mj_1}
\end{array}
\right),\dots,
\left(\begin{array}{c}
a_{i1j_t}\\
\vdots\\
a_{mj_t}
\end{array}
\right)
$$
は線型独立です。
従って、\(t\leq s\)となります。
以上により、前半と合わせて\(t=s\)です。
(3.\(\Leftrightarrow\)4.)
簡単です。
与えられた行列\(A\)の転置行列\(A^\top\)を考えます。
\(A^\top\)に関する3.の\(t\)を\(t^\prime\)とすると、そもそも転置行列の行列式はもとの行列式と一致するので、\(t=t^\prime\)です。
\(A^\top\)の列ベクトルは\(A\)の行ベクトルなので、2.\(\Leftrightarrow\)3.の結果から\(t=u\)です。
いじょうから\(t=u\)です。
(4.\(\Leftrightarrow\)5.)
一般に、\(S[\boldsymbol{a}_1^\prime,\dots,\boldsymbol{a}_n^\prime]\)の次元は\(\boldsymbol{a}_1^\prime,\dots,\boldsymbol{a}_n^\prime\)から選びうる線型独立なベクトルの最大個数に等しいのことから従います。
定理9.の証明終わり
要するに、行列のランクを求めたければ、求める手段が2.から5.の4パターンある、ということになります。
問題によって求めやすいものを用いましょう、ということです。
結
今回は行列のランクについてエクストリームに解説しました。
行列のランクは大きく分けて2つの定め方がありますが、イメージしやすいのは
です。
また、線型独立なベクトルの個数ともランクは対応しているため、4つほど求めるパターンがあります。
次回は連立一次方程式と行および列基本変形について解説します。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする