「レオンチェフ方程式〜グラフ理論の応用(産業連関②)〜」【幾何学の基礎シリーズ】グラフ理論編 その13

本記事の内容

本記事は、グラフ理論の応用の1つである産業連関のレオンチェフ方程式について解説する記事です。

本記事を読むにあたり、産業連関について知っている必要があるため、以下の記事も合わせてご覧ください。

「グラフ理論の応用〜産業連関①(産業連関とは？)〜」【幾何学の基礎シリーズ】グラフ理論編 その12

...

for-spring.com

2022.10.07

前回の話の軽い復習

産業連関表とは以下のような表でした。

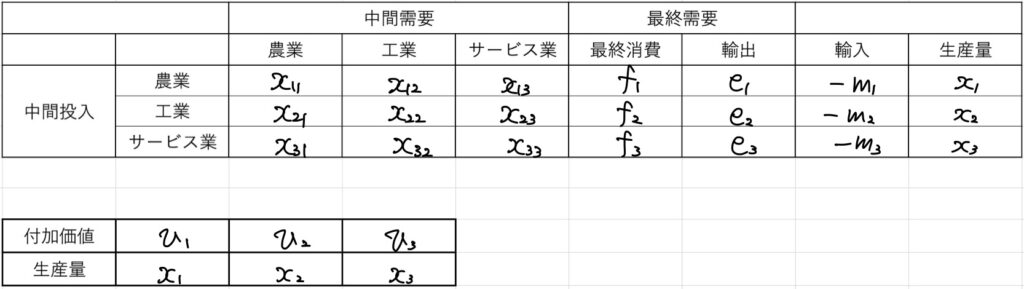
上記の表において、農業部門には1、工業部門には2、サービス部門には3の数字を当てています。
このとき

• $x_i$：部門$i$の生産量
• $x_{ij}$：部門$i$の生産量から部門$j$により需要され、使われる量
• $f_i$：部門$i$の生産量から消費財として需要され使われる量
• $e_i$：部門$i$の生産量から海外(輸出)のために需要され、使われる量
• $m_i$：部門$i$に輸入で海外から供給される量

を表しています。

$x_1,x_2,x_3$と$b_1,b_2,b_3$の間の関係式を表せば、次の関係式を得るのでした。
$$\begin{eqnarray} &&a_{11}x_1+a_{12}x_2+a_{13}x_3+b_1=x_1\\ &&a_{21}x_1+a_{22}x_2+a_{23}x_3+b_2=x_2\\ &&a_{31}x_1+a_{32}x_2+a_{33}x_3+b_3=x_3 \end{eqnarray}$$

これを見ると連立方程式ですね。

詳しくは、【幾何学の基礎シリーズ】グラフ理論編 その12を御覧ください。

産業部門の数が一般の個数の場合は？

前回の産業部門が3つの場合を一般の個数の場合に拡張します。

拡張すると…

複数の産業部門に番号を付けて、それらを$1,2,\dots,n$と表すことにします。
そして、ある年度の産業連関表が次のように与えられたとします。

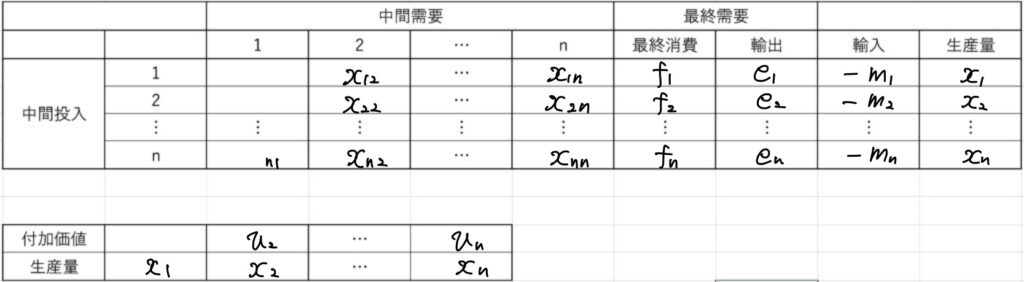
投入係数を$a_{ij}$、すなわち部門$i$からの生産量の内、部門$j$に需要されて使われる量は$x_{ij}=a_{ij}x_j$とします。
ただし、$a_{ij}=0$の場合は、$i$から$j$には供給が無い、と考えます。
部門$i$にシステムの外部から需要される量は$b_i=f_i+e_i-m_i$です。
従って、需要量に見合った生産が行われたのであれば、一般の場合も次の等式を得ることが出来ます。

$$\begin{eqnarray} x_1&=&a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n+b_1\\ x_2&=&a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n+b_2\\ \tag{1} \vdots&&\quad\vdots\qquad \quad\vdots\qquad\quad\qquad\quad \vdots\quad \quad\vdots\\ x_n&=&a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n+b_n\\ \end{eqnarray}$$

ここで、右辺が需要量、左辺が生産量を表しています。
もし、正の付加価値が付けられるならば、更に不等式
$$a_{1j}+a_{2j}+\cdots+a_{nj}<1\tag{2}$$
が成り立ちます。

これらは、ある年の産業連関表から得られる等式と不等式です。

レオンチェフ方程式(均衡産出高モデル)

ここで、産業連関表のことは一旦忘れて、この等式を、$a_{ij}\geq0$が予め与えられたとき(これも投入係数呼ぶことにしますが、不等式(2)は仮定しません)、最終需要料(厳密には輸入量を引いたもの)$b_1,\dots,b_n\ (b_i\geq0)$に対して、それに見合う生産量(均衡産出高)$x_1,\dots,x_n\ (x_i\geq0)$を求める連立方程式と見ます。
要するに、$a_{ij}\geq0$が与えられたときに、$b_1,\dots,b_n\ (b_i\geq0)$に対して$x_1,\dots,x_n\ (x_i\geq0)$を求める連立方程式と見る、ということです。

この方程式(1)をレオンチェフ方程式あるいは均衡産出高モデルといいます。

勿論、係数$a_{ij}$と$b_i$は産業連関表から得られる数値の場合は、レオンチェフ方程式は解を持ちます。
しかしながら、$b_1,\dots,b_n$を変化させたときに解を持つかどうか、ということは分かりません。
また、産業連関表から得られる投入係数$a_{ij}$を変化させたり、$0$以上の定数として独立に与えたときにも解を持つかどうかということは分かりません。

そこで、次のように定めます。

証明したいこと

今までの話から、次の定理を示すことが目標です。

これは特に、最終需要料(-輸入量)が正、または付加価値が正であるような産業連関表から得られる投入係数はviableだ、ということを意味しています。
勿論、「成り立ちそうだな」という定理です。

産業連関表の投入係数表から得られる行列
$$A= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}\\ \end{pmatrix}$$
を投入係数行列(technology matrix, input-output table)といいます。
投入係数行列の成分は$0$以上です。

これがどうしてグラフ理論と関係するんですか？

産業部門とそれらの間の需要・供給の関係は「ネットワーク」の形をしています。
これを数学的に定式化するのに、有向グラフの概念を使うのです。

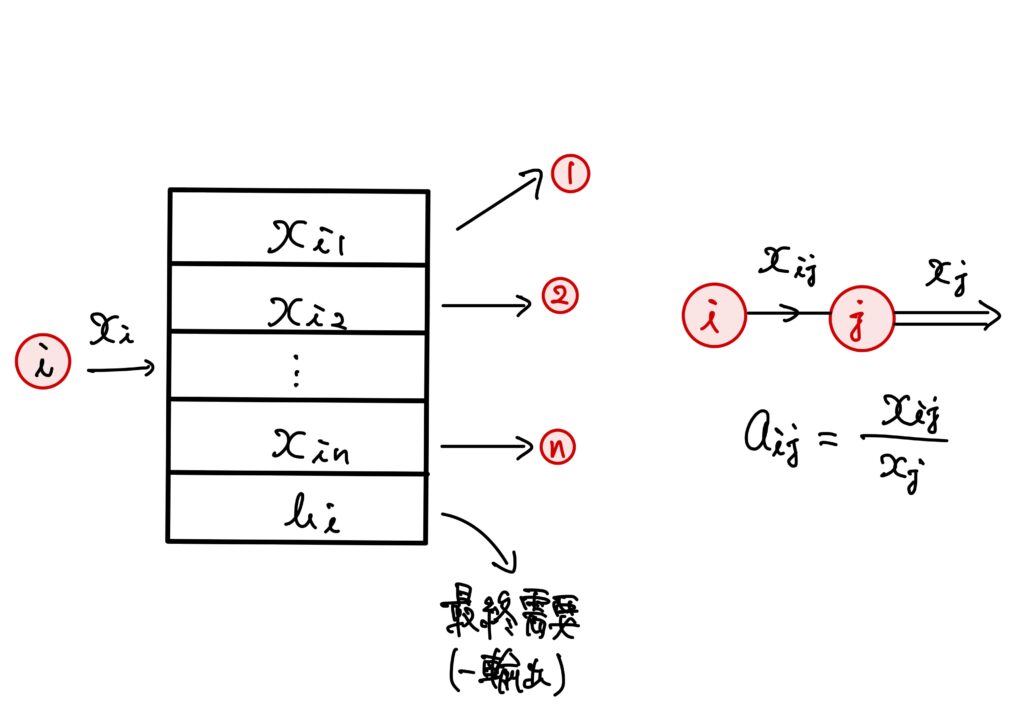
投入係数行列から、以前に述べた方法で有向グラフを作ります。
つまり、

• 各部門には頂点を対応させます。
  故に頂点には$1$から$n$までの番号が振られます。
• 部門$i$から部門$j$に供給があるときは(つまり$a_{ij}>0$のときは)、頂点$i$を始点として、頂点$j$を終点とする有向辺(供給の方向を指しています)が対応します。

経済システムに付随するグラフは連結としてOKです。
でなければ(連結でなければ)、互いに需要・供給のない独立なシステムに分解することが出来るからです。
要するに、別々で考えようよ、ということになってしまうからです。

余談(レオンチェフ方程式の応用先)

1. 需要の生産誘発力
最終需要が変化した時の(「数学的」解としての)産出変化から、需要変化が経済全体に与える影響力の大小を検討することができます。
2. 生産活動の国際依存度
国際的な産業連関表を用いて、貿易による国際分業を通じて、アメリカやアジアの最終需要(消費・投資)に日本産業の生産がどのように依存しているか、あるいは日本の最終需要に(日本以外の)アジア産業の生産がどの程度依存しているかを分析できます。
3. 経済計画
将来の最終需要変化を予測し、これを満たす各産業の将来市場規模から、不況化する産業や下火にある産業の存在を検知してその対策を講じます。
4. 景気問題
内需拡大の影響を使途別産業別に分析し、同じ財政規模でより効果的な景気対策(財政支出政策)を見出します。
5. 物価・コスト問題
為替レートの変化が輸入を通じて国内物価に与える影響や、賃金・資本コスト・間接税などの変化が財・サービス価格に与える影響を分析します.
6. 教育労働問題
産業別の雇用行列を使用して、産業別技能別の労働需要変化を求め、教育・失業・職業訓練などの動向を把握します。

皆様のコメントを下さい！

今回のジョークです。

まさにジョークですね。
数学者の「入ったら誰もいなくなる」というのは$2-3=-1$人が建物に居る、という仮想的な状況を認めれば、もう1人入ることで「$-1+1=0$人=誰もいない」という状態になるよね、ということです。
勿論、ありえませんので、まさにジョークです。

他にご存知のジョークがあれば是非コメントで教えて下さい！

結

今回は、産業連関のレオンチェフ方程式とは何か？について解説しました。
今回もグラフ理論のお話がありませんでしたが、産業連関が、特にレオンチェフ方程式がどのようにグラフ理論とつながるかというイントロをお話しました。

次回はレオンチェフ方程式に対して数学的に踏み込んでみます。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

グラフ理論についてより詳しく知りたい方は以下を参考にすると良いと思います！