本記事の内容
本記事は「実数の連続性」のイメージを説明する記事です。
また「なぜ実数の連続性が必要なのか」ということについても説明します。
集合および論理の初歩についても解説しておりますので、以下の記事も合わせて御覧ください。
※【論理と集合シリーズ】と銘打ってシリーズ化しているため、その一部のリンクを貼っています。
↓論理の初歩
↓集合の初歩
実数の連続性って?
「実数の連続性の前に、実数とは何かネ?」となっているかもしれませんが、実は高校数学で実は出現しています。
高校数学では「実数は有理数と無理数を合わせた数」というように導入されているようです。
これは正しいです。
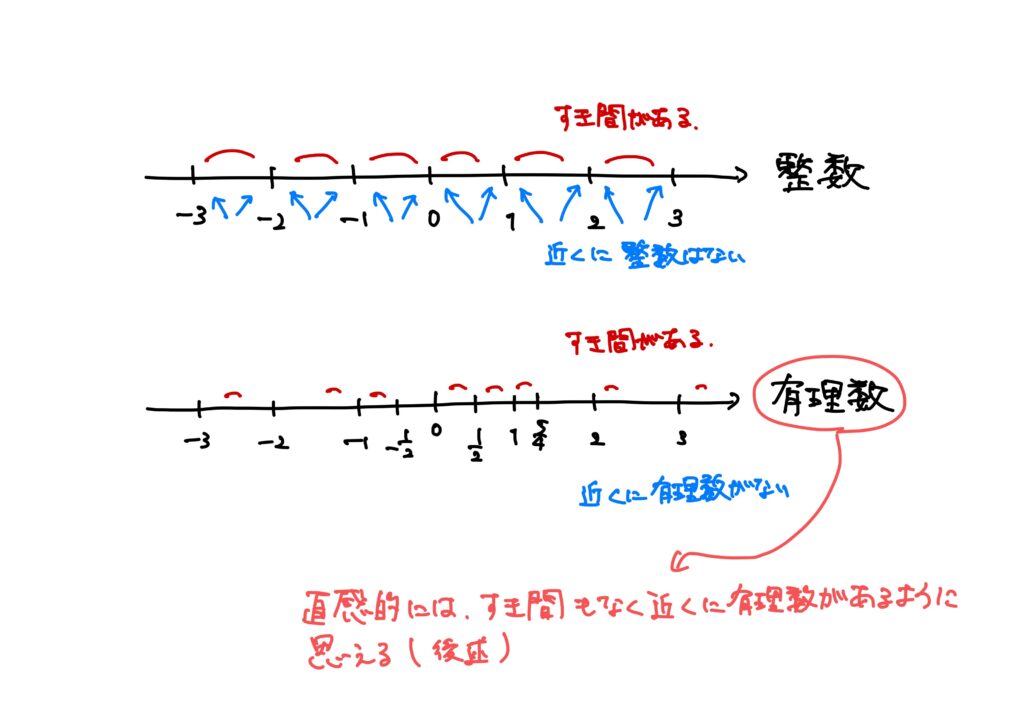
このとき、実数の連続性は直感的には
- 実数の数直線上には一切”すき間”が無い。
- どんな実数にもその十分近くにまた実数がある。
と言い換えられます。
特に、「どんな実数にもその十分近くにまた実数がある」という事実のおかげで”極限”が考えられるのです。
例えば、整数の数直線上はすき間だらけであるし、有理数の数直線にも隙間があります(別記事参照)。
実数の連続性と同値な命題
実数の連続性と同値な命題がおおよそ6つあります(他にもあります)。
- デデキントの切断(特にデデキントの定理)
- ワイエルシュトラスの上限公理
- 有界な単調列は収束する。
- 区間縮小法+アルキメデスの原理
- ボルツァーノ-ワイエルシュトラスの定理
- アルキメデスの原理+コーシー列の収束
「厳ついネ」と思うかもしれませんが、大丈夫です。
ちゃんと解説します。
要は、この6つは全て同値ということで、上記の6つのうち、どれを仮定しても、他5つが導ける、というわけです。
実数の連続性を考える意義
「意義は何か?」と言われれば、
ということです。
つまり、言ってしまえば、連続性というものが担保されていない世界(自然数とか、整数とか、有理数とか)では解析学を考えることはほぼ不可能なのです。
筆者に解析学の初歩を教えてくださった数学者曰く、
だそうです。
そして、その極限が考えられるのは、連続性が担保されている世界に限る、というわけです。
その連続性が担保されている世界の一例が、「実数の世界」なのです。
結
今回は、実数の連続性のイメージとその意義について述べました。
次回は「デデキントの切断、デデキントの定理とその証明」です。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする