本記事の内容
本記事は「点列って何?数列と違うの?」「点列の極限」について解説する記事です。
本記事を読むにあたり数列の収束について知っている必要があるため、その際は以下の記事を参照してください。
点列って?数列と違うの?
「点列と数列って違うの?」と言われたら「違うが似たようなものだネ」といったところです。
というのも、数列の多変数バージョンが点列だからです。
さらに言えば、ベクトルの列が点列です。
(正直なところ、点列のイメージはそんなもんです。)

より数学的に表現しましょう。
以前、「実数列は\(\mathbb{N}\)から\(\mathbb{R}\)への写像だ」という話をしました(「数列?」「有界?」「単調列?」【解析学の基礎シリーズ】)。
つまり実数列というのは、番号(自然数)に対して、その番号(自然数)に対する実数を対応付ける規則のことです。
例えば、数列\(\{a_n\}_{n\in\mathbb{N}}\)を\(a_n=2n-1\)で定めたとしましょう。
これは、「番号と呼ばれる自然数\(n\)に対して、奇数\(2n-1\)を対応付けた列」と捉えることができます。
それゆえ、実数列は\(\mathbb{N}\)から\(R\)への写像だ、と表現できるわけです。
点列、すなわち実数列の多次元バージョンもほとんど同じです。
答えを先に言ってしまえば、「点列は\(\mathbb{N}\)から\(\mathbb{R}^m\)への写像だ」です。
\(\mathbb{R}^m=\mathbb{R}\times \mathbb{R}\times \cdots \times \mathbb{R}\)、すなわち、\(\mathbb{R}\)の\(m\)個の直積集合です。
「直積集合?」となっている方は【論理と集合シリーズ】その6を御覧ください。
つまりどういうことか、ということを表したのが以下の図です。
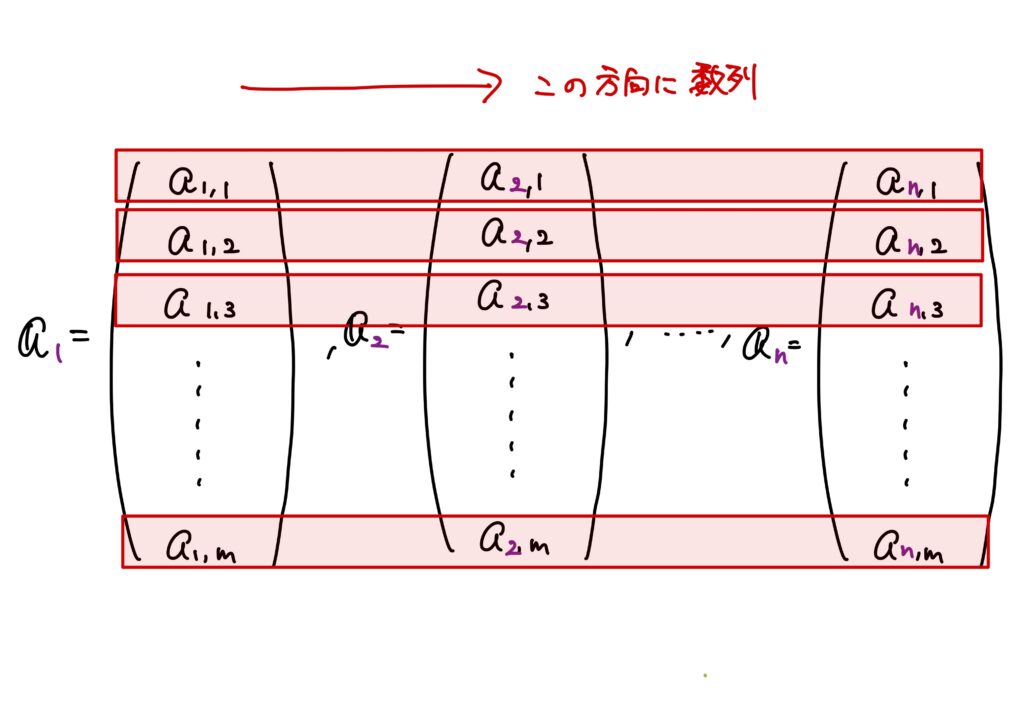
ここで、「点列は数列のベクトルではないヨ」ということを注意しておきます。
数列のベクトルだと項数が有限個になってしまって、点列ではなくなってしまいます。
数列は\(\{a_n\}_{n\in\mathbb{N}}\)と書きましたが、点列は太字にしたバージョンで\(\{\boldsymbol{a}_n\}_{n\in\mathbb{N}}\)と書きます。
※Wordpressだと太字と言うよりフォントが変わっているだけっぽいですが….
数列の収束の復習と点列の収束のイメージ
点列にも収束を考えることができます。
というより、点列の収束の1次元バージョンが数列の収束です。
「多次元になると難しいのかな?」と思うかもしれませんが、形式的には何ら問題ではありません。
上で述べたように、点列はベクトルの数列なので、各成分は数列の項です。
従って、各成分で考えればそれぞれ数列だからなのです。
それ故、各成分だけに目を向ければ、数列の収束そのものです。
ここで、軽く数列の収束のイメージを復習しておきましょう。
数列のイメージの復習(チャラめ)
「ちゃんと知りたい!」「ちゃんと思い出したい!」という方は「数列の収束って?」〜直感から論理へ〜【解析学の基礎シリーズ】を御覧ください。
ここではチャラく復習します。
一言で述べれば、
ということでした。
「\(a\)と\(b\)十分近い」というのは「\(a\)と\(b\)の”距離が”十分近い」ということで「任意の\(\epsilon>0\)に対して\(|a-b|<\epsilon\)」が成り立つことでした。
つまり、数列、すなわち1次元の場合の距離は絶対値で表現できることから、「どんな正の実数\(\epsilon\)に対しても、ある番号以降の数列の値については\(|a_n-A|<\epsilon\)が成り立っていることが収束ですよ」という話でした。
これを論理式で書くと、
というわけでした。
では、点列について見ていきましょう。
点列の収束のイメージ
点列の場合も本質的には同じです。
つまり、「ある番号以降の点列の値が、ある実数と”距離が”十分近いときに収束するという。」というわけです。
ここで疑問が生まれてくるかと思います。
「多次元のときも距離は絶対値なの?そのままでいいの?」ということです。
これは多次元の場合、単なる絶対値では表現できません。
「点列の値ってなんだっけ?」ということを思い出してみましょう。
点列はベクトルの数列だ、という説明をしました。
従って、点列の各値、すなわち点列\(\{{\boldsymbol{a}}_n\}_{n\in\mathbb{N}}\)の\(m\)番目の値(第\(m\)項の値)\({\boldsymbol a}_m\)はベクトルなのです。
従って、ベクトルにおける”距離”はそのベクトルの大きさです。
記号で書けば、ベクトル\(\boldsymbol{a}=(a_1,a_2,\dots,a_n)^\top\)の大きさ\(|\boldsymbol{a}|\)は
$$|\boldsymbol{a}|=\sqrt{a_1^2+a_2^2+\cdots+a_n^2}$$
です。
ただし、\(\boldsymbol{a}^\top\)はベクトル\(\boldsymbol{a}\)の行と列を入れ替えた(転置した)ベクトルのことです。
これで、「ベクトル同士が十分近い」ということを表現できました。
では、点列の収束を数学的に明示しましょう。
で?”点列の収束”は何なのかネ?
今更ながらこのブログには筆者が大好きなジャンプの某漫画に出てくるマッドサイエンティスト(厳密に正しいかはわかりませんが)がちょくちょく出現します。
あまり登場させると「ピイピイと五月蝿い事だヨ」と言われてしまうかもしれませんの注意します。
さて、余談は置いておいて、点列の収束を論理式で書くと次になります。
このように形式的には数列の極限と何ら変わりません。
より視覚的にわかりやすくするよう、上記の論理式を書き換えてみましょう。
とはいえ、書き換える部分は「\(|\boldsymbol{a}_n-\boldsymbol{A}|<\epsilon\)」の部分だけです。
\(\boldsymbol{A}\)も\(\boldsymbol{a}_n\)も\(\mathbb{R}^m\)の要素、すなわち\(m\)次元ベクトルです。
従って、
$$\boldsymbol{A}=
\left(
\begin{array}{c}
A_1 \\
A_2 \\
\vdots \\
A_m
\end{array}
\right),\quad
\boldsymbol{a}_n=
\left(
\begin{array}{c}
a_{n,1} \\
a_{n,2} \\
\vdots \\
a_{n,m}
\end{array}
\right)
$$
と書けます。
このとき、次が成り立ちます。
要は、点列の極限は、個々の数列の極限のベクトルと一致しますよ、ということです。
高校数学のノリでいうところの「\(\lim\)はカッコの中に入れてOK」ということです。
証明
これは数列の収束が分かっていれば、なんてことはありません。
\((\Rightarrow)\)の証明
示したいことは、
$$(\forall i\in\mathbb{N}:1\leq i\leq m)(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_{n,i}-A_i|<\epsilon)$$
です。
今、
$$(\forall \epsilon_0>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |\boldsymbol{a}_n-\boldsymbol{A}|<\epsilon_0)$$
が成り立っているので、
$$|\boldsymbol{a}_n-\boldsymbol{A}|=\sqrt{(a_{n,1}-A_1)^2+(a_{n,2}-A_2)^2+\cdots(a_{n,m}-A_m)^2}<\epsilon_0$$
が任意の\(\epsilon_0\)で成り立っています。
\(\epsilon_0\)は任意なので、新たに任意の\(\epsilon>0\)を用いて\(\epsilon_0\)を\(\epsilon\)と書き直します。
従って、
$$|\boldsymbol{a}_n-\boldsymbol{A}|=\sqrt{(a_{n,1}-A_1)^2+(a_{n,2}-A_2)^2+\cdots(a_{n,m}-A_m)^2}<\epsilon$$
が成り立っています。
ここで、\((a_{n,i}-A_i)^2\)は\(1\leq i\leq m\)で正です。
また、\(\displaystyle \sum_{i=1}^m(a_{n,i}-A_i)^2<\epsilon^2\)なのですから、
どの\(1\leq i\leq m\)を満たす\(i\in\mathbb{N}\)についても\(\displaystyle (a_{n,i}-A_i)^2<\epsilon^2\)でなければなりません。
故に、\(1\leq i\leq m\)を満たす任意の\(i\in\mathbb{N}\)に対して
$$|a_{n,i}-A_i| <\epsilon$$
となります。
従って、
$$(\forall i\in\mathbb{N}:1\leq i\leq m)(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_{n,i}-A_i|<\epsilon)$$
です。
\((\Leftarrow)\)の証明
示したいことは、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |\boldsymbol {a}_n-\boldsymbol{A}|<\epsilon)$$
です。
今、
$$(\forall i\in\mathbb{N}:1\leq i\leq m)(\forall \epsilon_0>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_{n,i}-A_i|<\epsilon_0)$$
が成り立っています。
\(\epsilon_0\)は任意なので、任意の\(\epsilon>0\)を用いて\(\displaystyle\epsilon_0=\frac{\epsilon^2}{m}\)としても成り立ちます。
従って、
\begin{eqnarray}
|\boldsymbol{a}_n-\boldsymbol{A}|&=&\sqrt{(a_{n,1}-A_1)^2+(a_{n,2}-A_2)^2+\cdots(a_{n,m}-A_m)^2}\\
&<&\sqrt{\frac{\epsilon^2}{m}+\frac{\epsilon}{m}^2+\cdots+\frac{\epsilon^2}{m}}\\
&=&\sqrt{m\cdot \frac{\epsilon^2}{m}}\\
&<&\sqrt{\epsilon^2}=\epsilon
\end{eqnarray}
となります。
従って、
$$(\forall i\in\mathbb{N}:1\leq i\leq m)(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_{n,i}-A_i|<\epsilon)$$
です。
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |\boldsymbol {a}_n-\boldsymbol{A}|<\epsilon)$$
です。
証明終わり
この定理の主張をより視覚的に表現すれば、
$$\lim_{n\to\infty}\boldsymbol{a}_n=\lim_{n\to\infty}
\left(
\begin{array}{c}
a_{n,1} \\
a_{n,2} \\
\vdots \\
a_{n,m}
\end{array}
\right)=
\left(
\begin{array}{c}\displaystyle
\lim_{n\to\infty}a_{n,1} \\
\displaystyle\lim_{n\to\infty}a_{n,2} \\
\vdots \\
\displaystyle\lim_{n\to\infty}a_{n,m}
\end{array}
\right)
$$
というわけです。
つまり、
というわけです。
「なんか、あまり数列と変わらないな」と思うかもしれません。
形式的にはそうです。
しかし、幾何的に(というと少々大げさですが)見ると違いが見えてきます。
点列の収束と数列の収束の違いは何かネ?
数列との違いは「対象がベクトルであること」です。
より直感的には「近づき方が多次元的だ」ということです。
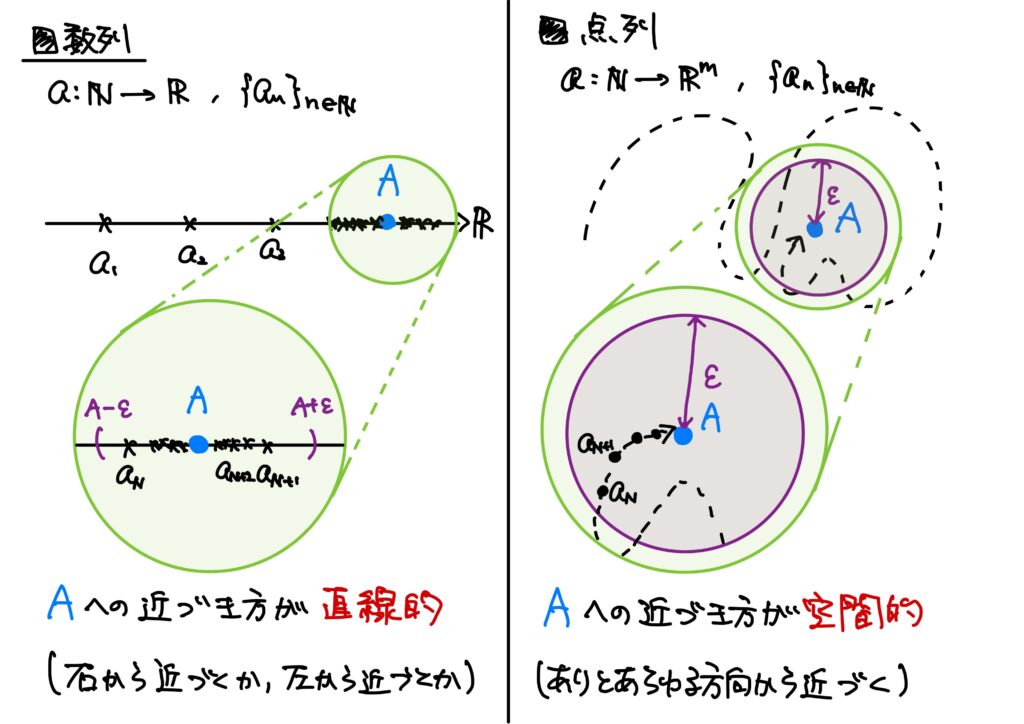
数列の極限への近づき方は1次元的でした。
しかし、点列はベクトルですので、近づき方が空間的です。
これが違いです。
実際に証明してみよう!
次の例を証明してみましょう。
例1. \(\displaystyle \lim_{n\to\infty}\left(1+\frac{1}{n},\frac{n+1}{n}\right)\)は\((1,1)\)に収束します。
証明
定理から、
$$\lim_{n\to\infty}\left( 1+\frac{1}{n} \right)=1,\quad \lim_{n\to\infty}\frac{n+1}{n}=1$$
を示せば良い事がわかります。
さらに、\(\displaystyle \lim_{n\to\infty}\left( 1+\frac{1}{n} \right)=1+\lim_{n\to\infty}\frac{1}{n}\)ですので、
$$\lim_{n\to\infty}\frac{1}{n}=0,\quad \lim_{n\to\infty}\frac{n+1}{n}=1$$
であれば良いです。
\(\displaystyle\lim_{n\to\infty}\frac{1}{n}=0\)については、「数列の収束って?」〜直感から論理へ〜【解析学の基礎シリーズ】ですでに証明しておりますので、そちらを御覧ください。
従って、\(\displaystyle \lim_{n\to\infty}\frac{n+1}{n}=1\)を示します。
(とはいえ、ほぼ\(\displaystyle\lim_{n\to\infty}\frac{1}{n}=0\)と同じです。)
示したいことは
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow \left|\frac{n+1}{n}-1\right|<\epsilon)$$
です。
これを満たすような番号\(N\)を見つけてきなさい、ということでした。
では、その番号はどんなものかを予想するために式変形してみましょう。
$$\left|\frac{n+1}{n}-1\right|=|1+\frac{1}{n}-1|=\left|\frac{1}{n}\right|=\frac{1}{n}$$
です。
従って、\(n\geq N\)のとき、\(\displaystyle \frac{1}{n}<\epsilon\)が任意の\(\epsilon>0\)で成り立つような番号\(N\)が存在すればいいわけです。
ということは、\(n\geq N\)のとき、\(\displaystyle \frac{1}{n}<\frac{1}{N}\)です。
故に\(\displaystyle\frac{1}{N}<\epsilon\)というような\(N\in\mathbb{N}\)があればいいわけです。
これはアルキメデスの原理から存在します。
くどいかもしれませんが、アルキメデスの原理は
でした。
アルキメデスの原理はどんな2つの正の実数\(a,b\)に対しても、\(b<N_0a\)を満たすような自然数\(N_0\)が取れる(見つけてくることができる)、という主張なのですから、\(b=1\)としても成り立ちます。
すなわち、
$$(\forall \epsilon>0)(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ 1<N_0\epsilon$$
が成り立ちます。
従って、任意の\(\epsilon>0\)に対して、\(\displaystyle \frac{1}{N_0}<\epsilon\)という\(N_0\)を見つけてくることができます。
\(N\)として\(N_0\)を採用すれば、\(n\geq N\)なる\(n\in\mathbb{N}\)に対して、
$$\left|\frac{n+1}{n}-1\right|=|1+\frac{1}{n}-1|=\left|\frac{1}{n}\right|=\frac{1}{n}<\frac{1}{N}<\epsilon$$
です。
従って、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow \left|\frac{n+1}{n}-1\right|<\epsilon)$$
です。
結
今回は点列とは何か、そしてその収束とはどういうことかについて説明しました。
とどのつまり、点列というのは数列の多次元バージョンで、点列の極限は各成分の極限ということでした。
ただ、極限への近づき方が1次元的から空間的にかわるよ、という話でした。
次回は、点列の極限における和、差の極限について解説します。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする