「全微分って？」【解析学の基礎シリーズ】偏微分編 その3

本記事の内容

本記事は全微分について解説する記事です。

本記事を読むにあたり、偏微分について知っている必要があるため、以下の記事も合わせてご覧ください。

「偏微分？」「高階微分？」「$C^k$級？」【解析学の基礎シリーズ】偏微分編 その1

...

for-spring.com

2022.07.22

全微分について筆者は最初、混乱しました。(内容とは関係ないので、読み飛ばしてOKです)

筆者が全微分を初めて学んだのは大学1年生のときでしたが、最初、混乱しました。
「全微分とはこれですよ」と言われた式が本当に理解できなかったからです。

それはどういう式だったか、というと(ここでは一旦2変数に絞ります)

です。

初めてこの式を見たときに「$dx$と$dy$って何？$\displaystyle \frac{dy}{dx}$って分数だったの？」と思いました。

通常、数学における数式は左辺を右辺で説明する、ということが多いです。
つまり、左辺に右辺でもって意味を持たせるわけです。
しかしながら、この式は右辺に不明な$dx$と$dy$が出てくるので、右辺の意味が分かりません。
故に$df$が実数なのか、ベクトルなのかすら分かりませんでした。
調べてみても、「$dx$と$dy$は無限小で…」とかいう説明が出てくるばかりで「無限小？そんな話今までしてましたっけ？」とより一層意味がわからなくなりました。
分からないまま講義は進み、「やっぱり分からない」ということで壁にぶつかりました。

とはいえ、いくら筆者が分からずともテストは待ってはくれません。
やむを得ず「そういうもんだ、ってことで覚えるか…」と諦めたくらいです(本当は良くないことです)。

後になって別の文献を見たときに、無限小や$dx$や$dy$という記号(“文字”と言った方が良いかもしれないな)を使わず、全微分を説明していて「あ、なんか分かった気がする。」となりました。

それが修士1年のときです。
4年越し、といったところです。
というのも、修士のときに学部生の講義のTA(ティーチング・アシスタント、講義補助みないなもの)をしたときに、微積分を担当しました。
その際に、「全微分を教えられないわけにはいかないよね…」ということで少々勉強したのです。

通常なら大学1年のときに「全微分ね。はいはい。分かります。」と理解するのでしょうが、筆者はできませんでした。

そんな紆余曲折があった中で筆者がたどり着いた全微分の理解をこの記事で説明しようと思います。

ちなみに、$df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy$はあくまで”形式的に”書いているだけに過ぎない、ということです。（後述します。）

1変数関数の微分の復習から始めましょう。

実は、偏微分編の最初の記事で、「１変数関数の微分に良く対応しているのは偏微分ではなく全微分です。」という話をサラッとしました。

そのため、まずは１変数の微分について復習します。

$I\subset\mathbb{R}$は$\mathbb{R}$の区間、$\boldsymbol{f}:I\to\mathbb{R}^m$を１変数関数とします。
$a\in I$であれば、
$$\begin{eqnarray} \boldsymbol{f}がa\in Iで微分可能&\Leftrightarrow&\lim_{h\to0}\frac{\boldsymbol{f}(a+h)-\boldsymbol{f}(a)}{h}が存在する。\\ &\Leftrightarrow&(\exists \boldsymbol{A}\in\mathbb{R}^m)\ {\rm s.t.}\ \lim_{h\to0}\frac{\boldsymbol{f}(a+h)-\boldsymbol{f}(a)}{h}=\boldsymbol{A}\\ &\Leftrightarrow&(\exists \boldsymbol{A}\in\mathbb{R}^m)\ {\rm s.t.}\ \lim_{h\to0}\frac{\boldsymbol{f}(a+h)-\boldsymbol{f}(a)-\boldsymbol{A}h}{|h|}=\boldsymbol{0}\\ \end{eqnarray}$$
でした。

もはやこれがほぼ全微分なのですが、この内容を思い出しておきましょう。

で、全微分ってなんですか？

では全微分について明示し、少しですがイメージを述べます。

全微分の明示

こうやって書いてくれると意味がわかるのですが、「$df=$うんぬん」と書かれても分かりませんでした。

全微分のイメージをサラッと。

さて、少しですが、全微分のイメージを述べておきます。

１変数の場合の微分を見てみると、実数$h$がだんだんと$0$に近づいていく、というイメージです。
実数なのですから、近づき方は２方向($+$の方向と$-$の方向)しかありません。

しかし、多変数の場合はベクトル$\boldsymbol{h}$が零ベクトル$\boldsymbol{0}$にだんだんと近づいていくので、近づく方向はありとあらゆる方向になります。
(※点列の収束と同じですね！)

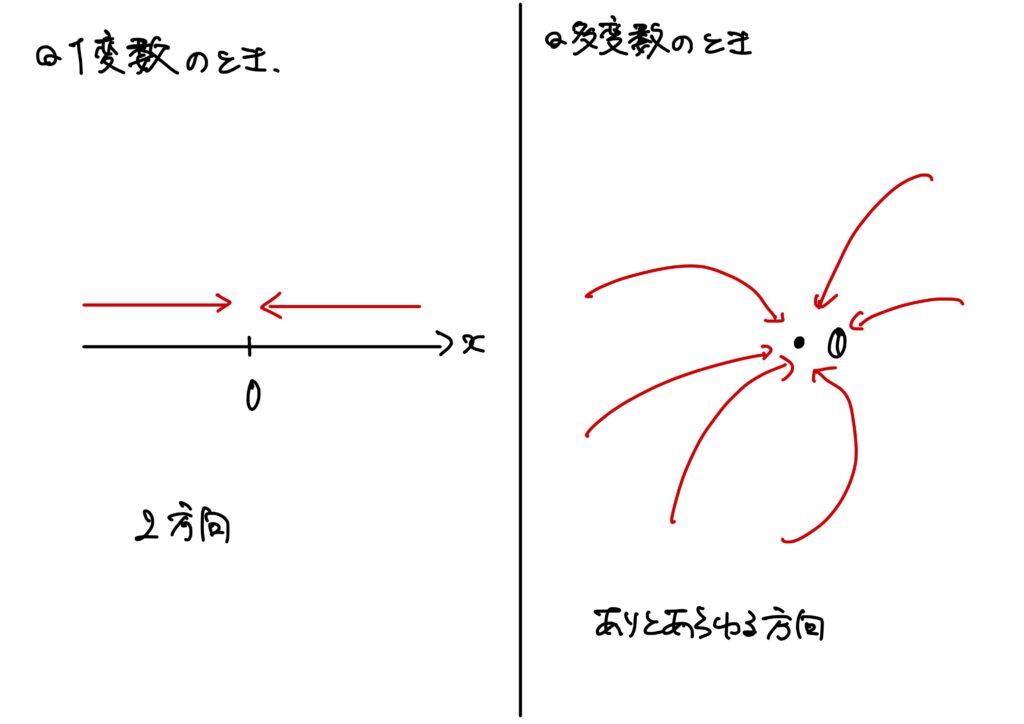
つまり、全微分とはありとあらゆる方向から$\boldsymbol{0}$に近づいてもその極限が存在しますよ、ということなので、ある種”全”方向で微分が可能だ、という状態のことを指しています(あくまでイメージですが)。

全微分可能性、連続性、偏微分可能性、$C^1$級の関係性とヤコビ行列(ヤコビアン)

では、全微分、連続性、偏微分、$C^1$級の関係性を表す事実を述べます。

ヤコビ行列(ヤコビアン)と行列のノルム

定理として主張を明示する前に、まずはヤコビ行列(ヤコビアン)と行列のノルムを説明します。

ヤコビ行列は多変数関数の極値を求めたりする際に使います(後の記事で解説します)。

次に行列のノルムです。

$M(m,n;\mathbb{R})$の要素$A$を、自然に(というより強引に、かな？)$\mathbb{R}^{mn}$の要素に対応させたとき、その$\mathbb{R}^{mn}$におけるノルムと$\|A\|$は一致するので、

$$\begin{eqnarray} &&\|A\|\geq0,\\ &&\|A\|=0\Leftrightarrow A=O,\\ &&\|A+B\|\leq\|A\|+\|B\|,\\ &&\|\lambda A\|=|\lambda|\cdot\|A\| \end{eqnarray}$$
が成り立ちます。

この行列のノルムの性質を１つ紹介します。

命題1.の証明

$A$の第$i$行ベクトルを転地したものを$\boldsymbol{a}_i\in\mathbb{R}^n$とします。
すなわち、
$$\boldsymbol{a}_i= \left( \begin{array}{c} a_{i1}\\ a_{i2}\\ \vdots\\ a_{in} \end{array} \right)$$
であり、
$$\begin{eqnarray} A= \left( \begin{array}{c} \boldsymbol{a}_1^\top\\ \boldsymbol{a}_2^\top\\ \vdots\\ \boldsymbol{a}_m^\top \end{array} \right),\quad \|A\|= \sqrt{\sum_{i=1}^m\sum_{j=1}^na_{ij}^2}=\sqrt{\sum_{i=1}^m\|\boldsymbol{a}_{i}\|^2},\quad A\boldsymbol{x}= \left( \begin{array}{c} \boldsymbol{a}_1^\top\boldsymbol{x}\\ \boldsymbol{a}_2^\top\boldsymbol{x}\\ \vdots\\ \boldsymbol{a}_m^\top\boldsymbol{x} \end{array} \right)= \left( \begin{array}{c} (\boldsymbol{a}_1,\boldsymbol{x})\\ (\boldsymbol{a}_2,\boldsymbol{x})\\ \vdots\\ (\boldsymbol{a}_m,\boldsymbol{x})\\ \end{array} \right) \end{eqnarray}$$
です。
ここで、ノルムの性質であるシュワルツの不等式を使います。

シュワルツの不等式は何だったか、というと、以下でした。

定理2.(シュワルツの不等式)の証明は【線型代数学の基礎シリーズ】固有値編 その5を御覧ください。

さて、シュワルツの不等式から
$$\|A\boldsymbol{x}\|^2=\sum_{i=1}^m(\boldsymbol{a}_i,\boldsymbol{x})\leq\sum_{i=1}^m\|\boldsymbol{a}_i\|^2\cdot\|\boldsymbol{x}\|^2=\left( \sum_{i=1}^m\|\boldsymbol{a}_i\|^2\right)\|\boldsymbol{x}\|^2=\|A\|\cdot\|\boldsymbol{x}\|^2$$
となるので、
$$\|A\boldsymbol{x}\|\leq\|A\|\cdot\|\boldsymbol{x}\|$$
です。

命題1.の証明終わり

全微分可能ならば、連続かつすべての変数に対して偏微分可能で、全微分係数はヤコビ行列です。

「全微分が”全”方向で微分可能だというイメージなんだったら、全微分可能ならばすべての変数に対して偏微分可能っていうのはそりゃそうじゃない？」となるかと思いますが、これを実際に証明してみます。

定理3.の証明

$\boldsymbol{f}$が$\boldsymbol{a}$で全微分可能なので、
$$\left( \exists A\in M(m,n;\mathbb{R})\right)\ {\rm s.t.}\ \lim_{\boldsymbol{h}\to\boldsymbol{0}}\frac{1}{\|\boldsymbol{h}\|}\left( \boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})-A\boldsymbol{h}\right)=\boldsymbol{0}$$
です。

(1.の証明)

$\boldsymbol{h}\to\boldsymbol{0}$のとき、命題1.から
$$\|A\boldsymbol{h}\|\leq\|A\|\cdot\|\boldsymbol{h}\|\to0$$
であるので、$\|A\boldsymbol{h}\|\to0$です。
また、
$$\begin{eqnarray} \boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})&=&\boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})\color{red}{-A\boldsymbol{h}+A\boldsymbol{h}}\\ &=&\|\boldsymbol{h}\|\cdot\frac{\boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})-A\boldsymbol{h}}{\|\boldsymbol{h}\|}+A\boldsymbol{h}\\ \end{eqnarray}$$
であるので、$\boldsymbol{h}\to\boldsymbol{0}$のとき、

$$\begin{eqnarray} \|\boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})\|&=& \left\| \|\boldsymbol{h}\|\cdot\frac{\boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})-A\boldsymbol{h}}{\|\boldsymbol{h}\|}+A\boldsymbol{h} \right\|\\ &\leq& \|\boldsymbol{h}\|\cdot\frac{\|\boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})-A\boldsymbol{h}\|}{\|\boldsymbol{h}\|}+\|A\boldsymbol{h}\|\to 0\cdot0+0=0 \end{eqnarray}$$
です。
故に、
$$\lim_{\boldsymbol{h}\to\boldsymbol{0}}\boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})=\boldsymbol{f}(\boldsymbol{a})$$
となるので、$\boldsymbol{f}$は$\boldsymbol{a}$で連続です。

(2.の証明)

$$\boldsymbol{f}= \left( \begin{array}{c} f_1\\ f_2\\ \vdots\\ f_m \end{array} \right),\quad A=\left( a_{ij}\right),\quad \boldsymbol{h}= \boldsymbol{f}= \left( \begin{array}{c} h_1\\ h_2\\ \vdots\\ h_n \end{array} \right)$$
とすると、
$$\left( \exists A\in M(m,n;\mathbb{R})\right)\ {\rm s.t.}\ \lim_{\boldsymbol{h}\to\boldsymbol{0}}\frac{1}{|\boldsymbol{h}|}\left( \boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})-A\boldsymbol{h}\right)=\boldsymbol{0}$$
において、第$i$成分は、
$$\lim_{\boldsymbol{h}\to\boldsymbol{0}}\frac{\displaystyle f_i(\boldsymbol{a}+\boldsymbol{h})-f_i(\boldsymbol{a})-\sum_{k=1}^na_{ik}h_k}{\|\boldsymbol{h}\|}=\boldsymbol{0}$$
です。
$j\in\{1,\dots,n\}$に対して、$\boldsymbol{h}=h\boldsymbol{e}_j$とすると、$\displaystyle\sum_{k=1l}^na_{ik}h_k=\sum_{k=1l}^na_{ik}h\delta_{kj}=a_{ij}h$($\delta$はクロネッカーのデルタです)であるから、
$$\lim_{h\to0}\frac{f_i(\boldsymbol{a}+h\boldsymbol{e}_j)-f_i(\boldsymbol{a})-a_{ij}h}{|h|}=0$$
です。
このことから、
$$\lim_{h\to0}\frac{f_i(\boldsymbol{a}+h\boldsymbol{e}_j)-f_i(\boldsymbol{a})}{h}=a_{ij}$$
です。
故に、$f_i$は$\boldsymbol{a}$で変数$x_j$について偏微分可能で、
$$\frac{\partial f_i}{\partial x_j}(\boldsymbol{a})=a_{ij}$$
故に、
$$A=\left( a_{ij}\right)=\left( \frac{\partial f_i}{\partial x_j}(\boldsymbol{a})\right)$$
となって、$A$はヤコビ行列です。

定理3.の証明終わり

ちなみに、

$C^1$級ならば、全微分可能

$C^k$級は”性質の良い”関数でした。
やはり、性質が良いので、全微分も可能なのです。

定理4.の証明

$\Omega$が開集合なので、
$$(\exists \epsilon>0)\ {\rm s.t.}\ B(\boldsymbol{a};\epsilon)\subset \Omega$$
が成り立っています。
任意の$i\in\{1,\dots,n\}$、$\boldsymbol{h}\in\mathbb{R}^n$、$0<\|\boldsymbol{h}\|<\epsilon$に対して、

$$\begin{eqnarray} f_i(\boldsymbol{a}+\boldsymbol{h})-f_i(\boldsymbol{a})&=& f_i(a_1+h_1,a_2+h_2,\dots,a_n+h_n)-f_i(a_1,a_2,\dots,a_n)\\ &=& f_i(a_1+h_1,a_2+h_2,\dots,a_n+h_n)-f_i(a_1,a_2+h_2,\dots,a_n+h_n)\\ &&+f_i(a_1,a_2+h_2,a_3+h_3,\dots,a_n+h_n)-f_i(a_1,a_2,a_3+h_3,\dots,a_n+h_n)\\ &&+f_i(a_1,a_2,a_3+h_3,\dots,a_n+h_n)-f_i(a_1,a_2,a_3,a_4+h_4,\dots,a_n+h_n)\\ &&\qquad \qquad \vdots\qquad \qquad \vdots\\ &&+f_i(a_1,a_2,\dots,a_{n-1},a_n+h_n)-f_i(a_1,a_2,\dots,a_{n-1},a_n)\\ \end{eqnarray}$$
です。

ここで、平均値の定理を使います。

定理5.の証明は【解析学の基礎シリーズ】１変数実数値関数の微分編 その8を御覧ください。

平均値の定理から、$\exists \theta_1,\theta_2,\dots,\theta_n\in(0,1)$が存在して、
$$f_i(\boldsymbol{a}+\boldsymbol{h})-f_i(\boldsymbol{a})=\sum_{j=1}^n\frac{\partial f_i}{\partial x_j}(a_1,\dots,a_{j-1},a_j+\theta_jh_j,a_{j+1}+h_{j+1},\dots,a_n+h_n)h_j$$
です。
故に、
$$f_i(\boldsymbol{a}+\boldsymbol{h})-f_i(\boldsymbol{a})-\sum_{j=1}^n\frac{\partial f_i}{\partial x_j}(\boldsymbol{a})h_j=\sum_{j=1}^n\epsilon_{ij}(h)h_j$$
です。
ただし、
$$\epsilon_{ij}(h)=\frac{\partial f_i}{\partial x_j}(a_1,\dots,a_{j-1},a_j+\theta_jh_j,a_{j+1}+h_{j+1},\dots,a_n+h_n)-\frac{\partial f_i}{\partial x_j}(\boldsymbol{a})\ (j=1,\dots,n)$$
です。
ここで、$\boldsymbol{h}\to\boldsymbol{0}$のとき、
$$\|(a_1,\dots,a_{j-1},a_j+\theta_jh_j,a_{j+1}+h_{j+1},\dots,a_n+h_n)-\boldsymbol{a}\|^2\leq\sum_{j=1}^nh_j^2=\|\boldsymbol{h}\|^2\to\boldsymbol{0}$$
であることと、$\boldsymbol{f}$は$C^1$級であることを仮定したので、$\displaystyle\frac{\partial f_i}{\partial x_j}$は連続だから、
$$\epsilon_{ij}(h)\to0$$
となります。
ここで、三角不等式と$|h_j|\leq \|\boldsymbol{h}\|\ (j=1,\dots,n)$であることを用います。

三角不等式とは以下でした。

定理6.(三角不等式)の証明は【線型代数学の基礎シリーズ】固有値編 その5を御覧ください。

さて、三角不等式と$|h_j|\leq \|\boldsymbol{h}\|\ (j=1,\dots,n)$を用いれば、
$$\frac{\displaystyle\left|\sum_{j=1}^n\epsilon_{ij}(\boldsymbol{h})h_j \right|}{\|\boldsymbol{h}\|}\leq\frac{\displaystyle\sum_{j=1}^n\left|\epsilon_{ij}(\boldsymbol{h})\right|\cdot\left|h_j \right|}{\|\boldsymbol{h}\|}\leq \sum_{j=1}^n\left|\epsilon_{ij}(\boldsymbol{h}) \right|\to0\ (\boldsymbol{h}\to\boldsymbol{0})$$
となるので、
$$\frac{\displaystyle f_i(\boldsymbol{a}+\boldsymbol{h})-f_i(\boldsymbol{a})-\sum_{j=1}^n\frac{\partial f_i}{\partial x_j}(\boldsymbol{a})h_j}{\|\boldsymbol{h}\|}=\frac{\displaystyle \sum_{j=1}^n\epsilon_{ij}(\boldsymbol{h})h_j}{\|\boldsymbol{h}\|}\to0\ (\boldsymbol{h}\to\boldsymbol{0})$$
これは$f_i$が$\boldsymbol{a}$で全微分であることを示しています。
従って、$\boldsymbol{f}$も$\boldsymbol{a}$で全微分可能です。

定理4.の証明終わり

さて、この定理について少々述べておきます。

定理4.から関数の１階偏導関数をすべて求めて(多項式の形をしていたりすると簡単に求まります)、それらが連続関数であることが確かめられれば、その関数が全微分可能だということが分かります。
これは、与えられた関数が全微分可能であることを確かめるのに誠に強力な手段です。

ちなみに、定理4.の証明では、$\boldsymbol{f}$がすべての１階偏導関数を持ち、それらが連続だ、ということしかつかていません。
つまり、$\boldsymbol{f}$そのものが連続かどうかということは使っていません。
それで全微分可能だ、ということが示されたわけですので、定理3.から「全微分可能ならば連続」なので、$\boldsymbol{f}$は連続です。

全微分可能、連続、$C^1$級の関係性のまとめ

条件がごちゃごちゃしているので、ここでまとめておきます。

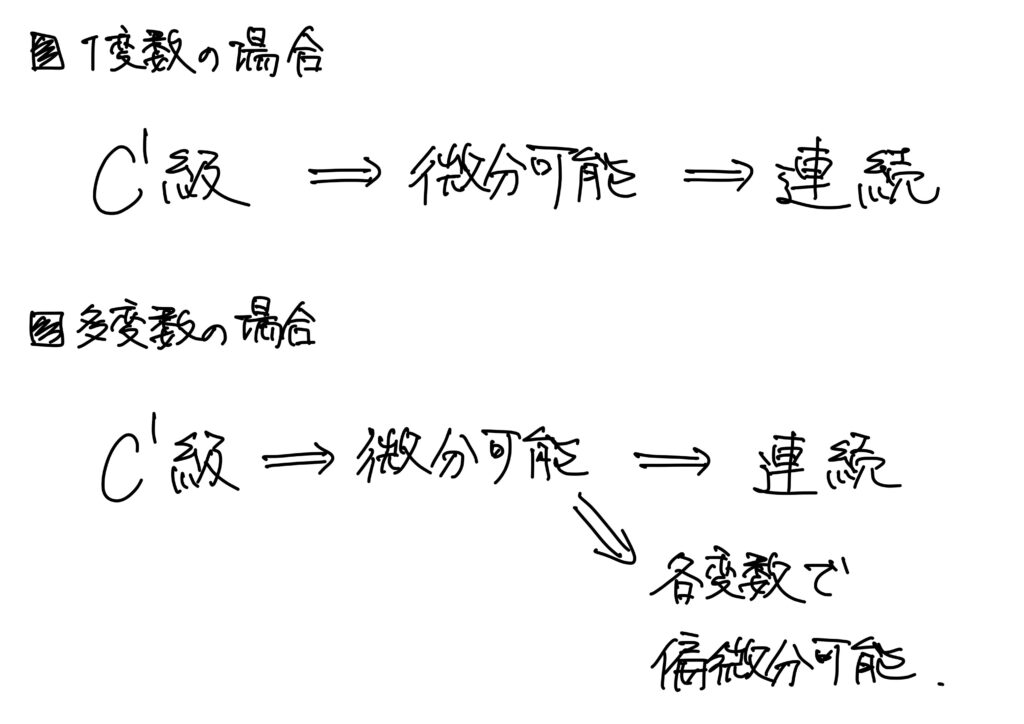
全微分可能であることを示す戦略

ここでは全微分可能かを示す戦略について述べます。

一般的な戦略

まずは偏微分を試みます。
定理3.から「全微分可能ならば偏微分可能」なので、対偶をとって「偏微分可能でないならば全微分可能でない」からです。
すべての変数について偏微分可能であることを確認した後、偏導関数が連続かどうかを調べます。
もし連続なのであれば、元の関数は$C^1$級なので、全微分可能です。

仮に連続でない場合は、各$i$について、
$$\lim_{\boldsymbol{h}\to\boldsymbol{0}}\frac{1}{\|\boldsymbol{h}\|}\left( f_i(\boldsymbol{a}+\boldsymbol{h})-f_i(\boldsymbol{a})-\sum_{j=1}^n\frac{\partial f_i}{\partial x_j}(\boldsymbol{a})h_j\right)=0$$
かどうかを調べます。
これが成り立てば、$\boldsymbol{f}$は全微分可能です。
※$\displaystyle\sum_{j=1}^n\frac{\partial f_i}{\partial x_j}(\boldsymbol{a})h_j$はヤコビ行列$A$と$\boldsymbol{h}$の積の第$i$成分です。

でも実際には…

連続関数でやったときと同様に(合成関数の微分はまだ説明していないのでネタバラシになってしまいますが…)、$C^\infty$級の関数から組み立てた関数もまた$C^\infty$級です。
多項式関数や、高校で学んだ関数は基本的に定義域全体で$C^\infty$級です。
$f(x)=|x|$やらは例外ですが。

故に、関数が与えられたときに、「これは$C^\infty$級の関数を組み立てたものだな」ということが分かれば、定理4.から「$C^1$級ならば全微分可能」なので、全微分可能です。

実際に確かめてみましょう。

してみましょう。

例7.$f:\mathbb{R}^2\to\mathbb{R}$を$f(x,y)=\sqrt{x^2+y^2}$で定めます。
このとき、$f$が全微分可能かを判定してみます。

$g(t)=\sqrt{t}\ (t\geq0)$、$\varphi(x,y)=x^2+y^2$としたとき、$f=g\circ\varphi$です。
$g$も$\varphi$も連続な関数なので、その合成関数$f$もまた連続です。
では、戦略として偏微分可能かを調べてみます。

$$\lim_{h\to0}\frac{f(0+h,0)-f(0,0)}{h}=\lim_{h\to0}\frac{\sqrt{h^2}-0}{h}=\lim_{h\to0}\frac{|h|}{h}$$
となりますが、これは極限が存在しません。
従って、$f$は$(0,0)$で$x$について偏微分可能ではありません。
定理3.から「全微分可能ならば偏微分可能」で、この対偶「偏微分可能でないならば全微分可能でない」から、$f$は全微分可能ではありません。

ちなみに、$C^1$級の関数とは、「各変数に付き偏微分可能で、かつ偏導関数がすべて連続な関数」のことだったので、$f$は$x$で偏微分可能でないから、$C^1$級ではありません。

例8.(ペアノの例) $\displaystyle f(x,y)= \begin{cases} \displaystyle xy\frac{x^2-y^2}{x^2+y^2}&((x,y)\neq(0,0))\\ 0&((x,y)=(0,0)) \end{cases}$
の全微分可能性を調べてみます。
ちなみに、この例は偏微分の順序交換が成り立たないのでした。

さて、まずは偏微分可能かを確かめます。

$$f_x(0,0)=\lim_{k\to0}\frac{f(0+k,0)-f(0,0)}{k}=\lim_{h\to0}\frac{\displaystyle k\cdot0\cdot \frac{k^2-0^2}{k^2+0^2}-0}{k}=\lim_{k\to0}0=0\\ f_y(0,0)=\lim_{k\to0}\frac{f(0,0+k)-f(0,0)}{k}=\lim_{h\to0}\frac{\displaystyle 0\cdot k\cdot \frac{0^2-k^2}{0^2+k^2}-0}{k}=\lim_{k\to0}0=0\\ $$

従って、$f$は$(0,0)$で$x$および$y$のそれぞれについて偏微分可能です。

$(x,y)\neq(0,0)$とすると、
$$f_x(x,y)=\frac{y(x^4+4x^2y^2-y^4)}{(x^2+y^2)^2},\ f_x(x,y)=\frac{x(x^4-4x^2y^2-y^4)}{(x^2+y^2)^2}$$
です。
また、$(x,y)\to(0,0)$で
$$\left| f_x(x,y)-f_x(0,0)\right|\leq|y|\cdot\frac{y(x^4+2x^2y^2+y^4)}{(x^2+y^2)^2}\leq 2|y|\cdot\frac{y(x^4+4x^2y^2-y^4)}{(x^2+y^2)^2}=2|y|\to0\\ \left| f_y(x,y)-f_y(0,0)\right|\leq|x|\cdot\frac{y(x^4+2x^2y^2+y^4)}{(x^2+y^2)^2}\leq 2|x|\cdot\frac{y(x^4+4x^2y^2-y^4)}{(x^2+y^2)^2}=2|x|\to0$$
ですので、$C^1$級です。
定理4.から「$C^1$級ならば全微分可能」なので、$f$は全微分可能です。

全微分と接平面

$f$が$(a,b)$で全微分可能であるときに形式的に
$$df=\frac{\partial f}{\partial x}(a,b)dx+\frac{\partial f}{\partial y}(a,b)dy$$
と書きます。
この記号の意味のイメージを述べます。

これは一言でいうと、$f$の１次近似を表します。
つまり、$(a,b)$における$f$の接平面です。

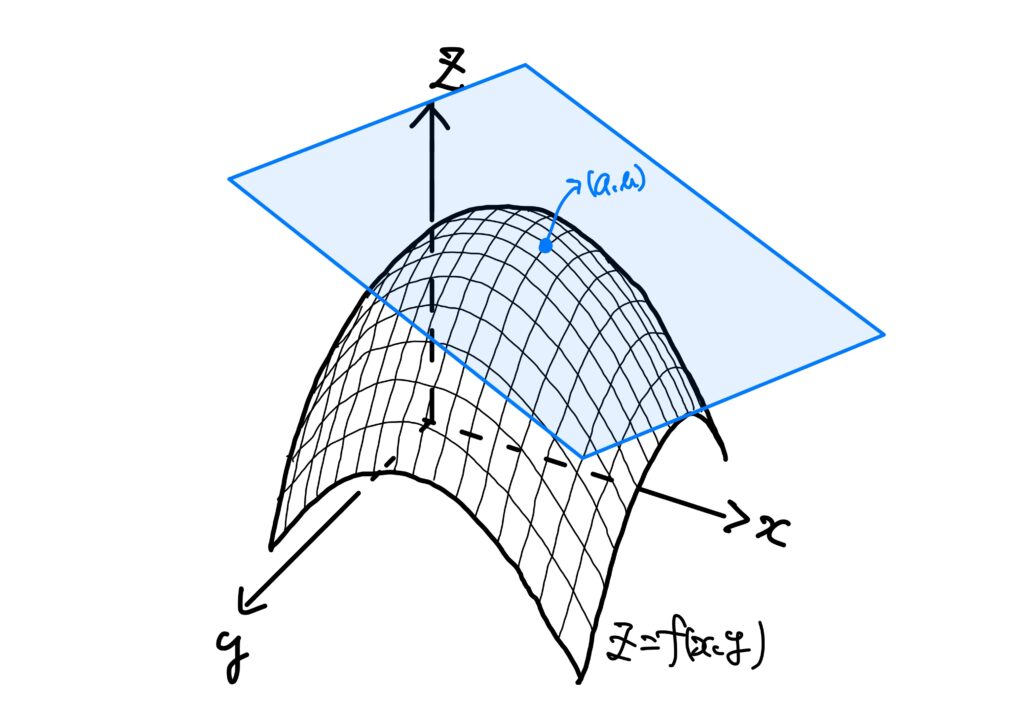
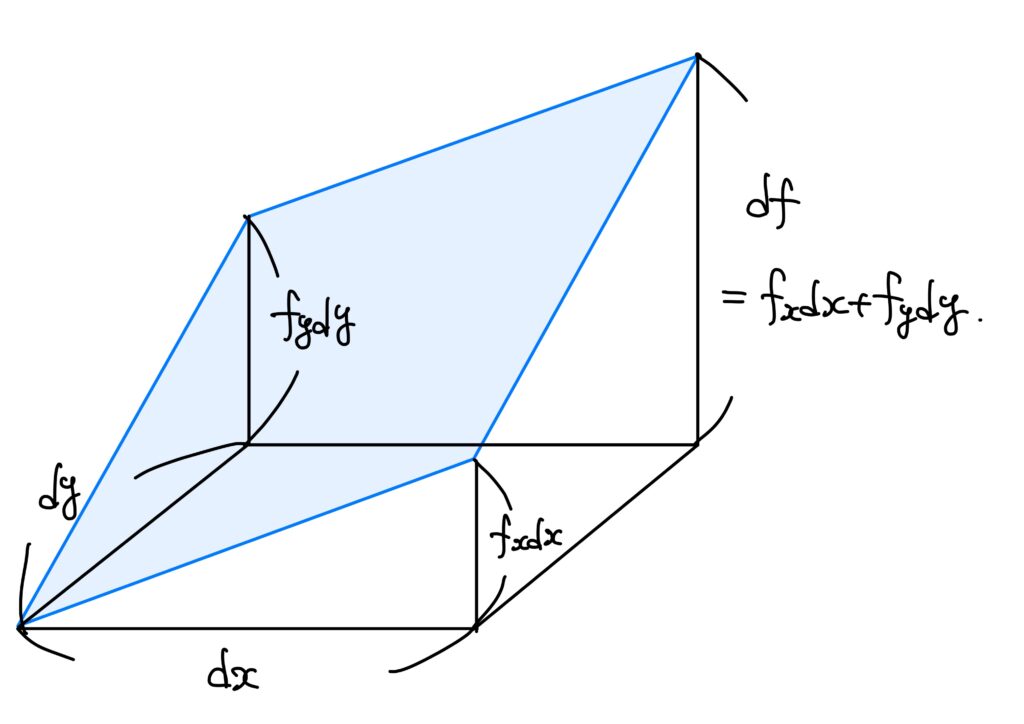
$dx,dy,df$というのは、微小量(めちゃくちゃちっちゃい量)を表しています。
点$(a,b)$から微小量$(dx,dy)$だけ移動すると、$f(x,y)$の微小変化量$df$は、接平面による近似により、おおよそ$df=f_xdx+f_ydy$になりますよ、ということです。

結

今回は、全微分について解説しました。
全微分可能というのは偏微分と違ってイメージとしてはありとあらゆる方向で微分可能、ということです。
また、全微分可能であれば、連続かつすべての変数で微分可能で、$C^1$級ならば全微分可能なので、関数の連続性を吟味するには全微分可能性は非常に強力です。

また、全微分は接平面に対応しています。

次回はヤコビ行列と勾配についてもう少し詳しく解説します。

乞うご期待！質問、コメントなどお待ちしております！