本記事の内容
本記事は1変数ベクトル値関数の無限大における極限について解説する記事です。
本記事を読むにあたり、ベクトル値関数の極限について知っている必要があるため、その際は以下の記事を参照してください。
また、実数値関数の場合を理解しているとより、イメージがつきやすいと思われますので、その際は以下の記事を参照してください。
実数値関数の場合のチャラい復習
1変数の場合をチャラく復習します。
- \(x\to\infty\)のときの\(A\)への収束 \(I=(\alpha,\infty)\)のとき、関数\(f\)が\(A\)に収束するとは、次が成り立つことをいう。 $$(\forall \epsilon>0)(\exists U’\in\mathbb{R})\ {\rm s.t.}\ (\forall x\in I:x>U’\Rightarrow |f(x)-A|<\epsilon)$$ このとき、 $$\lim_{x\to \infty}f(x)=A$$ と書く。
- \(x\to-\infty\)のときの\(A\)への収束 \(I=(\infty,\beta)\)のとき、関数\(f\)が\(A\)に収束するとは、次が成り立つことをいう。 $$(\forall \epsilon>0)(\exists L’\in\mathbb{R})\ {\rm s.t.}\ (\forall x\in I:x<L’\Rightarrow |f(x)-A|<\epsilon)$$ このとき、 $$\lim_{x\to -\infty}f(x)=A$$ と書く。
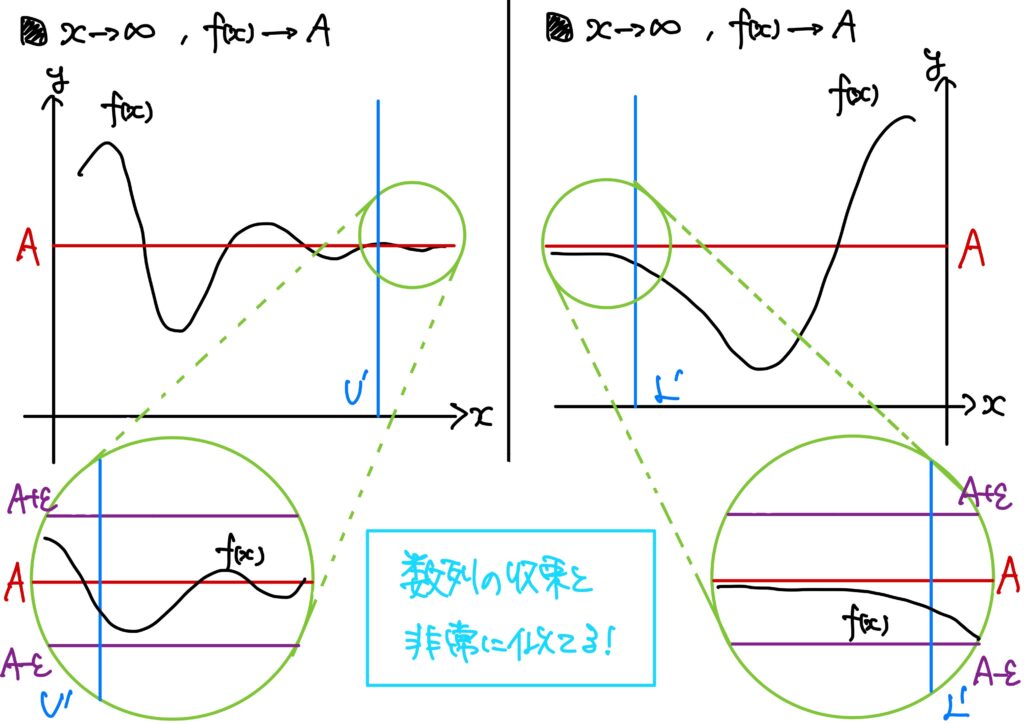
要は、平たく言えば、
ある\(L’\in\mathbb{R}\)以前の実数\(x\)については、\(f(x)\)と\(A\in\mathbb{R}\)の距離が十分近いときに、\(\displaystyle\lim_{x\to -\infty}f(x)=A\)と書く。
ということでした。
詳しくは【解析学の基礎シリーズ】関数の極限編 その18を御覧ください。
ベクトル値関数の場合
正直なところ、実数値関数のときとほとんど同じです。
実数値関数の場合は、ある\(U’\in\mathbb{R}\)以降の実数\(x\)については、\(f(x)\)と\(A\in\mathbb{R}\)の距離、すなわち、「実数と実数の距離」が十分近いときに、\(\displaystyle\lim_{x\to \infty}f(x)=A\)と書く、ということです。
一方ベクトル値関数の場合は、ある\(U’\in\mathbb{R}\)以降の実数\(x\)については、\(\boldsymbol{f}(x)\)と\(\boldsymbol{A}\in\mathbb{R}^m\)の距離、すなわち、「ベクトルとベクトルの距離」が十分近いときに、\(\displaystyle\lim_{x\to \infty}\boldsymbol{f}(x)=\boldsymbol{A}\)と書く、という単にそれだけです。
これを数学的に書くと、次です。
- \(x\to\infty\)のときの\(\boldsymbol{A}\)への収束 \(I=(\alpha,\infty)\)のとき、ベクトル値関数\(\boldsymbol{f}\)が\(\boldsymbol{A}\)に収束するとは、次が成り立つことをいう。 $$(\forall \epsilon>0)(\exists U’\in\mathbb{R})\ {\rm s.t.}\ (\forall x\in I:x>U’\Rightarrow |\boldsymbol{f}(x)-\boldsymbol{A}|<\epsilon)$$ 言い換えれば、 $$ \boldsymbol{f}(x)= \left( \begin{array}{c} f_1(x)\\ f_2(x)\\ \vdots \\ f_m(x)\\ \end{array} \right),\quad \boldsymbol{A}= \left( \begin{array}{c} A_1\\ A_2\\ \vdots \\ A_m\\ \end{array} \right) $$ と書いたとき、 $$(\forall \epsilon>0)(\exists U’\in\mathbb{R})\ {\rm s.t.}\ \left(\forall x\in I:x>U’\Rightarrow \sqrt{\sum_{i=1}^m\left(f_i(x)-A_1\right)^2}<\epsilon\right)$$ が成り立つことを言う。 このとき、 $$\lim_{x\to \infty}\boldsymbol{f}(x)=\boldsymbol{A}$$ と書く。
- \(x\to-\infty\)のときの\(\boldsymbol{A}\)への収束 \(I=(-\infty,\beta)\)のとき、関数\(\boldsymbol{f}\)が\(\boldsymbol{A}\)に収束するとは、次が成り立つことをいう。 と書いたとき、 $$(\forall \epsilon>0)(\exists U’\in\mathbb{R})\ {\rm s.t.}\ \left(\forall x\in I:x>U’\Rightarrow \sqrt{\sum_{i=1}^m\left(f_i(x)-A_i\right)^2}<\epsilon\right)$$ が成り立つことを言う。 このとき、 $$\lim_{x\to \infty}\boldsymbol{f}(x)=\boldsymbol{A}$$ と書く。
- \(x\to-\infty\)のときの\(\boldsymbol{A}\)への収束 \(I=(-\infty,\beta)\)のとき、関数\(\boldsymbol{f}\)が\(\boldsymbol{A}\)に収束するとは、次が成り立つことをいう。 $$(\forall \epsilon>0)(\exists L’\in\mathbb{R})\ {\rm s.t.}\ (\forall x\in I:x<L’\Rightarrow |\boldsymbol{f}(x)-\boldsymbol{A}|<\epsilon)$$ 言い換えれば、 $$ \boldsymbol{f}(x)= \left( \begin{array}{c} f_1(x)\\ f_2(x)\\ \vdots \\ f_m(x)\\ \end{array} \right),\quad \boldsymbol{A}= \left( \begin{array}{c} A_1\\ A_2\\ \vdots \\ A_m\\ \end{array} \right) $$ と書いたとき、 $$(\forall \epsilon>0)(\exists L’\in\mathbb{R})\ {\rm s.t.}\ \left(\forall x\in I:x<L’\Rightarrow \sqrt{\sum_{i=1}^m\left(f_i(x)-A_i\right)^2}<\epsilon\right)$$ が成り立つことを言う。 このとき、 $$\lim_{x\to -\infty}\boldsymbol{f}(x)=\boldsymbol{A}$$ と書く。
ね?そのまんまでしょ?
本当に成り立つのかネ?
もちろん成り立ちます。
簡単ではありますが、例を挙げましょう。
例1. \(\boldsymbol{f}:\mathbb{R}\setminus\{0\}\to\mathbb{R}^2\)が
$$
\boldsymbol{f}(x)=
\left(
\begin{array}{c}
e^{\frac{1}{x}}\\
e^{\frac{1}{2x}}\\
\end{array}
\right)
$$
で定められているとします。
\(x\to\infty\)のとき、\(\boldsymbol{f}(x)\to (0,0)\)です。
証明
示したいことは、
$$(\forall \epsilon>0)(\exists U’\in\mathbb{R})\ {\rm s.t.}\ \left(\forall x\in I:x>U’\Rightarrow \sqrt{\left(e^\frac{1}{x}\right)^2+\left(e^\frac{1}{2x}\right)^2}<\epsilon\right)$$
です。
要は、上記のような\(U’\in\mathbb{R}\)を見つけたいわけです。
もし仮に、任意の\(\epsilon>0\)に対して、上記のような\(U’\in\mathbb{R}\)があったとしたら、\(x>U’\)を満たす\(x\in\mathbb{R}\)において、
$$
\sqrt{\left(e^\frac{1}{x}\right)^2+\left(e^\frac{1}{2x}\right)^2}<\sqrt{\left(e^\frac{1}{U’}\right)^2+\left(e^\frac{1}{2U’}\right)^2}
$$
ですので、
$$
\sqrt{\left(e^\frac{1}{U’}\right)^2+\left(e^\frac{1}{2U’}\right)^2}<\epsilon
$$
となってほしいわけです。
従って、
$$
\sqrt{\left(e^\frac{1}{U’}\right)^2+\left(e^\frac{1}{2U’}\right)^2}=\epsilon
$$
の解が\(U’\)の候補です。
これを解けば、\(\displaystyle U’=\frac{2}{\displaystyle\log\frac{-1+\sqrt{4\epsilon+1}}{2}}\)です。
故に、\(\displaystyle U’=\frac{2}{\displaystyle\log\frac{-1+\sqrt{4\epsilon+1}}{2}}\)とすることで、
$$(\forall \epsilon>0)(\exists U’\in\mathbb{R})\ {\rm s.t.}\ \left(\forall x\in I:x>U’\Rightarrow \sqrt{\left(e^\frac{1}{x}\right)^2+\left(e^\frac{1}{2x}\right)^2}<\epsilon\right)$$
です。
証明終わり
例1. \(\boldsymbol{f}:\mathbb{R}\setminus \{0\}\to\mathbb{R}^2\)が
$$
\boldsymbol{f}(x)=
\left(
\begin{array}{c}
e^{\frac{1}{x}}\\
e^{\frac{1}{2x}}\\
\end{array}
\right)
$$
で定められているとします(さっきと同じです)。
\(x\to-\infty\)のとき、\(\boldsymbol{f}(x)\to (0,0)\)です。
証明
示したいことは、
$$(\forall \epsilon>0)(\exists U’\in\mathbb{R})\ {\rm s.t.}\ \left(\forall x\in I:x<L’\Rightarrow \sqrt{\left(e^\frac{1}{x}\right)^2+\left(e^\frac{1}{2x}\right)^2}<\epsilon\right)$$
です。
先程とほとんど同じです。
要は、上記のような\(L’\in\mathbb{R}\)を見つけたいわけです。
もし仮に、任意の\(\epsilon>0\)に対して、上記のような\(L’\in\mathbb{R}\)があったとしたら、\(x<L’\)を満たす\(x\in\mathbb{R}\)において、\(L'<0\)であれば、
$$
\sqrt{\left(e^\frac{1}{x}\right)^2+\left(e^\frac{1}{2x}\right)^2}<\sqrt{\left(e^\frac{1}{L’}\right)^2+\left(e^\frac{1}{2L’}\right)^2}
$$
ですので、
$$
\sqrt{\left(e^\frac{1}{L’}\right)^2+\left(e^\frac{1}{2L’}\right)^2}<\epsilon
$$
となってほしいわけです。
従って、先程の\(U’\)を使って、\(L’=-U’\)であれば良い事がわかります。
つまり、\(\displaystyle L’=-\frac{2}{\displaystyle\log\frac{-1+\sqrt{4\epsilon+1}}{2}}\)です。
故に、\(\displaystyle -L’=\frac{2}{\displaystyle\log\frac{-1+\sqrt{4\epsilon+1}}{2}}\)とすることで、
$$(\forall \epsilon>0)(\exists L’\in\mathbb{R})\ {\rm s.t.}\ \left(\forall x\in I:x<L’\Rightarrow \sqrt{\left(e^\frac{1}{x}\right)^2+\left(e^\frac{1}{2x}\right)^2}<\epsilon\right)$$
です。
証明終わり
結
今回は\(\displaystyle\lim_{x\to\pm\infty}\boldsymbol{f}(x)=\boldsymbol{a}\)について解説しました。
結局の所実数値関数の場合と何ら変わりません。
ただ「距離が近い」というところが実数値関数の場合と違ってベクトル同士の距離が近い、という意味になるだけです。
次回は、いよいよ微分法に入っていきます!
まずは高校数学の復習ということで、1変数実数値関数の微分法について解説します。
※もちろん、高校数学で微積分を習っていない、または「んなもん忘れたわ」という方にも読んで頂けるよう必要なことをエクストリームで解説します。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする