「ワイエルシュトラスの最大値定理(多次元版)のイメージをつかもう！」「$\mathbb{R}^n$の開集合、閉集合」【解析学の基礎シリーズ】多変数関数編 その17

本記事の内容

本記事は多次元ver.のワイエルシュトラスの最大値定理のイメージと$\mathbb{R^n}$における開集合、閉集合について説明する記事です。

本記事を読むにあたり、１変数の場合のワイエルシュトラスの最大値定理を知っている必要があるため、その際は以下の記事を参照してください。

「ワイエルシュトラスの最大値定理を証明しよう！」〜連続な関数の性質〜【解析学の基礎シリーズ】関数の極限編 その16

本記事の内容本記事はワイエルシュトラスの最大値定理の証明を与える記事です。本記事を読むにあたり、関数の連続性とボルツァーノ-ワイエルシュトラスの定理を知っている必要があるため、その際は以下の記事を参照してください。↓関数の連続性の記事↓ボル

for-spring.com

ワイエルシュトラス%e3%81%ae%e6%9c%80%e5%a4%a7%e5%80%a4%e5%ae%9a%e7%90%86%e3%82%92%e8%a8%bc%e6%98%8e%e3%81%97%e3%82%88%e3%81%86%ef%bc%81%e3%80%8d%e3%80%9c%e9%80%a3%e7%b6%9a%e3%81%aa%e9%96%a2%e6%95%b0/#toc4

１次元の場合のワイエルシュトラスの最大値定理のチャラい復習

1次元の場合のワイエルシュトラスの最大値定理のイメージとしては単純なもので、

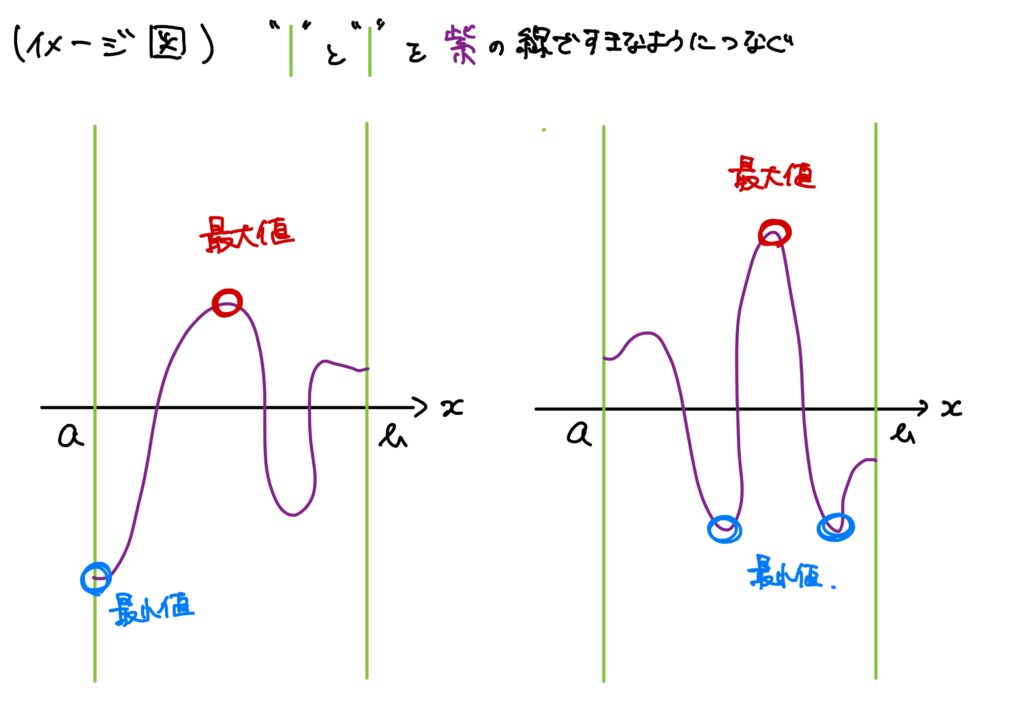
ということでした。
これを数学的に表現すると次でした。

多次元版のイメージも同じようなものです。
言ってしまえば、閉区間が閉領域、一般に閉集合に変わるだけです。
ただ、「閉領域(閉集合)とは何かネ？」という話ですので、まずはそれについて話します。

$\mathbb{R}^n$における開集合、閉集合

$\mathbb{R}$における開区間、閉区間の領域ver.のようなものです。

直感的には、

• 開集合：境界(縁)を含まない集合
• 閉集合：境界(縁)を含む集合

です。

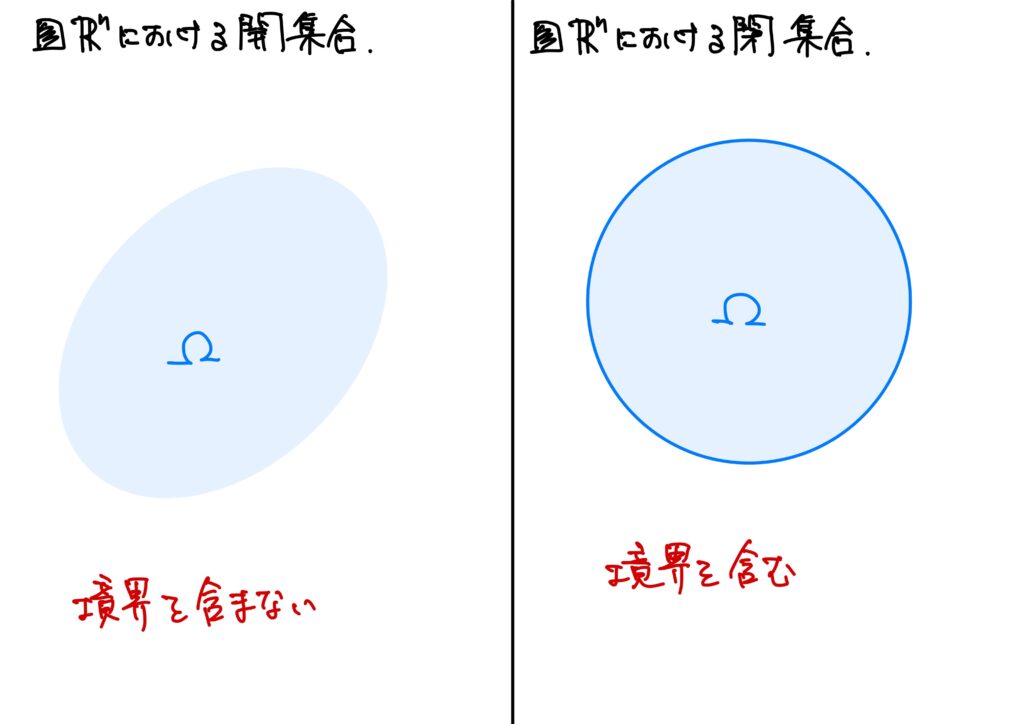
これを数学的に表すと、次です。

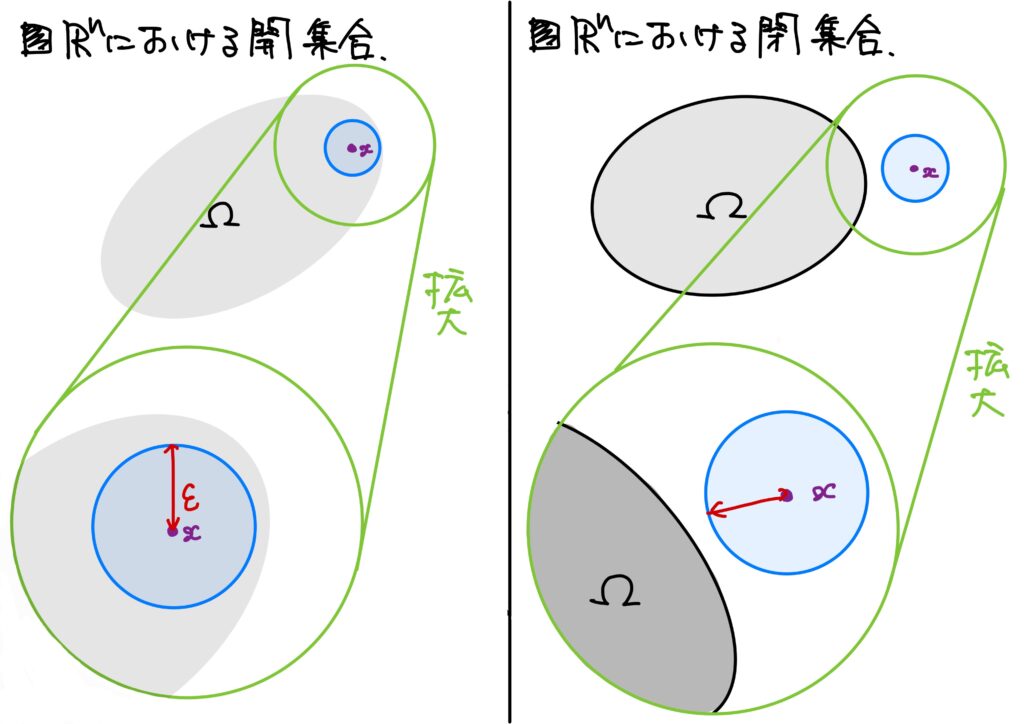
※注意※ 開かつ閉な集合もあります($\mathbb{R}$においては$\mathbb{R}$と$\emptyset$です)。

$\mathbb{R}^n$の閉集合には次の性質があります。

証明

1.$\Rightarrow$2.の証明

$\{\boldsymbol{a}_n\}_{n\in\mathbb{N}}$は$K$内の点列で、$\mathbb{R}^n$で$\boldsymbol{a}$に収束しているとします。
示したいことは、$\boldsymbol{a}\in K$です。
背理法により証明します。
仮に$\boldsymbol{a}\not\in K$、すなわち$\boldsymbol{a}\in K^c$としましょう。
$K$は$\mathbb{R}^n$の閉集合ですので、$K^c$は$\mathbb{R}^n$の開集合です。
従って、
$$(\forall \boldsymbol{x}\in K^c)\ (\exists \epsilon>0)\ {\rm s.t.}\ B(\boldsymbol{x};\epsilon)\subset K^c$$
が成り立ちます。
$\boldsymbol{x}\in K^c$は任意なので、$\boldsymbol{x}=\boldsymbol{a}$としても成り立ちます。
故に、
$$(\exists \epsilon>0)\ {\rm s.t.}\ B(\boldsymbol{a};\epsilon)\subset K^c$$
が成り立ちます。
一般に、集合$A,\ B$に対して$A\cap B=\emptyset \Leftrightarrow A\subset B^c$ですので、$B(\boldsymbol{a};\epsilon)\cap K=\emptyset$です。
ここで、$\displaystyle\lim_{n\to\infty}\boldsymbol{a}_n=\boldsymbol{a}$ですので、
$$(\forall \epsilon_0>0)\ (\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |\boldsymbol{a}_n-\boldsymbol{a}|<\epsilon_0)$$
が成り立っています。
この$\epsilon_0$は任意なので、$\epsilon_0=\epsilon$としても成り立ちます。
故に、
$$(\forall n\in\mathbb{N}:n\geq N\Rightarrow |\boldsymbol{a}_n-\boldsymbol{a}|<\epsilon)$$
です。
つまり、$n\geq N$を満たす任意の$n\in\mathbb{N}$に対しては、$\boldsymbol{a}_n\in B(\boldsymbol{a};\epsilon)$です。
さて、$\{\boldsymbol{a}_n\}_{n\in\mathbb{N}}$は$K$内の点列でしたので、任意の$n\in\mathbb{N}$に対して、$\boldsymbol{a}_n\in K$です。
すなわち、任意の$n\in\mathbb{N}$に対して、$\boldsymbol{a}_n\not\in K^c$です。
従って、$B(\boldsymbol{a};\epsilon)\subset K^c$により$\boldsymbol{a}_n\not\in B(\boldsymbol{a};\epsilon)$のはずです。
故に、$\boldsymbol{a}_n\in B(\boldsymbol{a};\epsilon)$と$\boldsymbol{a}_n\not\in B(\boldsymbol{a};\epsilon)$が同時に成り立ってしまったので矛盾です。
以上のことから$\boldsymbol{a}\in K$です。

2.$\Rightarrow$1.の証明

これも背理法で証明します。
$K$が$\mathbb{R}^n$の閉集合でないとしましょう。
すると、$K^c$は開集合でないので、
$$(\exists \boldsymbol{a}\in K^c)\ {\rm s.t.}\ (\forall \epsilon>0)\ B(\boldsymbol{a};\epsilon)\not\subset K^c$$
です。
従って、$B(\boldsymbol{a};\epsilon)\cap K\neq \emptyset$です。
この$\epsilon>0$は任意ですので、任意の$n\in\mathbb{N}$に対して、$\displaystyle\epsilon=\frac{1}{n}$としても成り立ちます。
$\{\boldsymbol{a}_n\}_{n\in\mathbb{N}}$は$K$内の点列でしたので、任意の$n\in\mathbb{N}$に対して$\boldsymbol{a}_n\in K$です。
故に、$\displaystyle\exists \boldsymbol{a}_n\in B\left(\boldsymbol{a};\frac{1}{n}\right)\cap K$です。
従って、任意の$\epsilon>0$に対して、$\displaystyle\frac{1}{N}<\epsilon$となるような$N\in\mathbb{N}$を選べば(アルキメデスの原理！)、
$$\forall n\in\mathbb{N}:n\geq N \Rightarrow \boldsymbol{a}_n\in B\left(\boldsymbol{a};\frac{1}{n}\right)\subset B\left(\boldsymbol{a};\frac{1}{N}\right)\subset B\left(\boldsymbol{a};\epsilon\right)$$
となるため、これはまさに$\displaystyle\lim_{n\to\infty}\boldsymbol{a}_n=\boldsymbol{a}$を表しています。
仮定から$\{\boldsymbol{a}_n\}_{n\in\mathbb{N}}$の極限は$K$の要素なので、$\boldsymbol{a}\in K$です。
故に$\boldsymbol{a}\in K^c$と$\boldsymbol{a}\not\in K^c$が同時に成り立ってしまったので矛盾です。
以上のことから$K$は閉集合です。

証明終わり

多次元版のワイエルシュトラスの最大値定理のイメージ

前置きが長くなってしまいましたが、多次元版のワイエルシュトラスの最大値定理のイメージを説明します。

一言で述べてしまえば、

ということです。
１次元版と何ら変わりません。

簡単ですが、例を挙げます。

例. $\Omega=\{\boldsymbol{x}\in\mathbb{R}^n\mid |\boldsymbol{x}|\leq1\}$とし、$f:\Omega\to\mathbb{R}$が$f(x,y)=x^2+y^2$で定められているとします。

このとき、$\Omega$は閉集合であり、かつ$f$は$\Omega$で連続です。
$f$は多項式関数ですので、$\Omega$で連続です(証明は【解析学の基礎シリーズ】多変数関数編 その12を御覧ください)。
$\Omega$閉集合であることについては簡単に証明できます。

$\Omega$が$\mathbb{R}^n$の閉集合であることの証明

示したいことは、
$$(\forall \boldsymbol{x}\in \Omega^c)\ (\exists \epsilon>0)\ {\rm s.t.}\ B(\boldsymbol{x};\epsilon)\subset \Omega^c$$
です。
要は、上記を満たす$\epsilon>0$を見つけてくれば良いというわけです。
$\Omega^c=\{\boldsymbol{z}\in\mathbb{R}^2\mid |\boldsymbol{z}|\geq 1\}$に注意します。
任意の$\boldsymbol{z}\in\Omega^c$に対して、$\epsilon=|\boldsymbol{z}|-1$とします。
すると、$\boldsymbol{w}\in B(\boldsymbol{z};|\boldsymbol{z}-1|)$は$|\boldsymbol{z}-\boldsymbol{w}|<|\boldsymbol{z}|-1$を満たします。
故に、
$$|\boldsymbol{z}|-|\boldsymbol{w}|\leq |\boldsymbol{z}-\boldsymbol{w}|<|\boldsymbol{z}|-1$$
により、$|\boldsymbol{w}|>1$です。
従って、$\boldsymbol{w}\in\Omega^c$ですので、$\Omega$は$\mathbb{R}^2$の閉集合です。

証明終わり

この$f$のグラフは次になります。

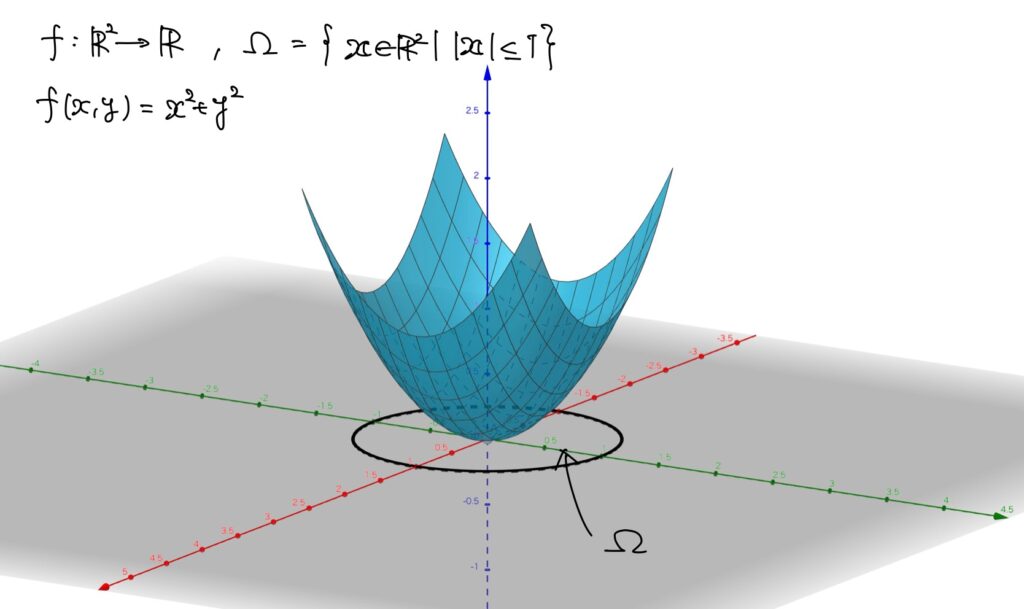
このとき、$f$は$x^2+y^2=1$を満たす$(x,y)$で最大値$1$を取ります。
つまり、$(a,b)\in\{(x,y)\in\mathbb{R}^2\mid x^2+y^2=1\}$に対して、$f(a,b)=1$です。
一方、$(x,y)=(0,0)$で最小値$0$を取ります。

このように、定義域が閉集合で、かつ定義域で連続な多変数実数値関数は必ず最大値と最小値があります。

結

今回は$\mathbb{R}^n$の開集合、閉集合、多次元バージョンのワイエルシュトラスの最大値定理のイメージを説明しました。

$\mathbb{R}^n$においての開集合のイメージは「境界(縁)を含まない集合」で、閉集合のイメージは「境界(縁)を含む集合」です。
多次元版ワイエルシュトラスの最大値定理のイメージとしては、

ということです。

次回は多次元版ワイエルシュトラスの最大値定理の証明と、その証明のために必要な点列の場合のボルツァーノ-ワイエルシュトラスの定理の証明をします。

乞うご期待！質問、コメントなどお待ちしております！