本記事の内容
本記事は数列が発散することを実際に証明する記事である。
本記事を読むにあたり数列が発散するとはどういうことかを理解していると理解が深まると思われるので、その際は以下の記事を参照してください。
数列が発散することを実際に証明してみよう!
例1.について

この命題の証明は難しくないので是非挑戦してみてほしい!
(証明)
示したいことは、\(a_n=n\)としたとき、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow a_n>U)$$
が成り立つことである。
すなわち、任意の実数\(U\)に対して、上記を満たすような番号\(N\)を見つけてくれば良い。
アルキメデスの原理から、
$$(\forall a\in\mathbb{R}_{>0})(\forall b\in\mathbb{R}{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ b|U|+1>U$$
が成り立つ。
従って、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow a_n>U)$$
が成り立ったので、\(\displaystyle \lim_{n\to\infty}n=\infty\)である。
(Q.E.D.)
この証明も「もし、こんな\(N\)があったらいいなあ」という期待からアルキメデスの原理に至る。
例2.について
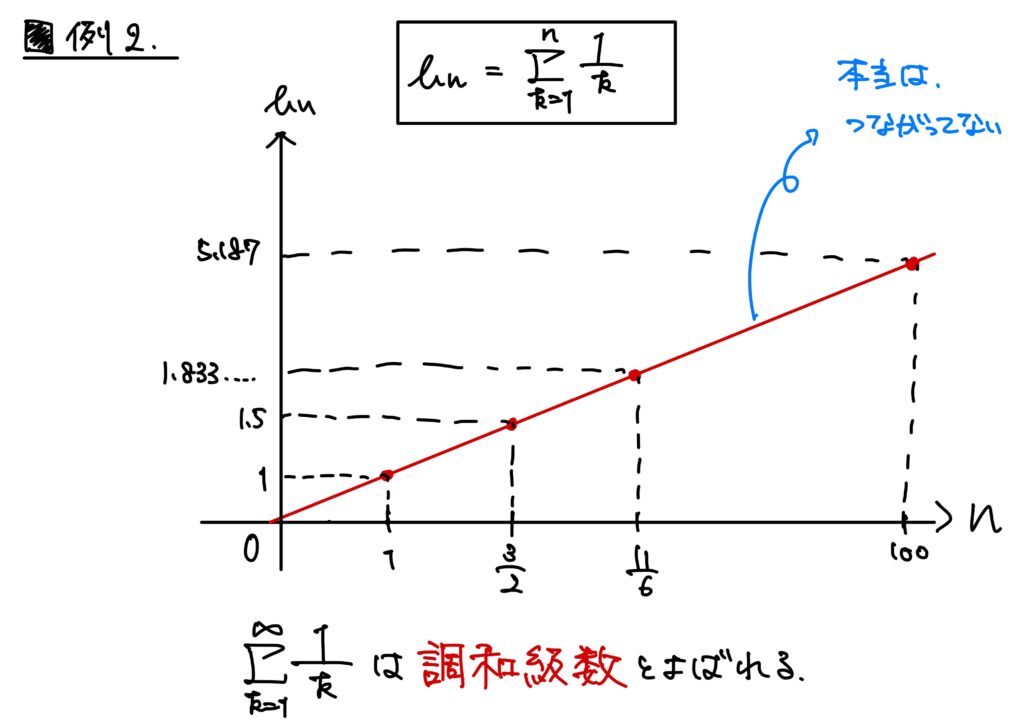
この数列は調和級数と呼ばれる有名な数列である。
この命題の証明は少々特殊なので、流れを説明する。
- (ステップ1) \(\displaystyle \sum_{k=1}^{n}\frac{1}{k}\)よりも小さい数列を取ってくる。
- (ステップ2) とってきた数列が発散することを示す。
- (ステップ3) 追い出しの原理を用いて\(\displaystyle \sum_{k=1}^{n}\frac{1}{k}\)が発散することを示す。
(証明)
(ステップ1)
任意の自然数\(n\)に対して、\(n\geq 2^m\)を満たす\(m\in\mathbb{N}\cup\{0\}\)が存在する。
実際、自然数\(n\)を素因数分解すると、\(n=2^i(2j+1)\)(\(i,j\in\mathbb{N}\cup\{0\}\))と書くことができる。(素因数分解して、偶数の部分と奇数の部分に分けた、ということ。)
すなわち、上記を満たすような\(i,j\in\mathbb{N}\cup\{0\}\)が存在する。
ここで、\(2^i(2j+1)\geq2^i\)であるから、\(m\)として\(i\)を採用すれば、任意の自然数\(n\)に対して、\(n\geq2^m\)という\(m\in\mathbb{N}\cup\{0\}\)が存在する。
従って、\(\displaystyle \sum_{k=1}^{n}\frac{1}{k}>\sum_{k=1}^{2^m}\frac{1}{k}\)が成り立つ。
ここで、1つ補題を与える。
(補題4.の証明)
数学的帰納法で証明する。
- \(m=1\)のとき
\(\displaystyle \sum_{k=1}^{2^1}=1+\frac{1}{2}=\frac{3}{2}\)であり、\(1+\displaystyle\frac{m}{2}=\frac{3}{2}\)であるから成り立つ。 - \(m=t\)のとき成り立つとする。
このとき、
$$\sum_{k=1}^{2^t}\frac{1}{k}\geq 1+\frac{t}{2}$$
が成り立つ。
\(m=t+1\)のとき、
$$\sum_{k=1}^{2^{t+1}}\frac{1}{k}\geq 1+\frac{t+1}{2}$$
が成り立てば良い。
\begin{eqnarray}
\sum_{k=1}^{2^{t+1}}\frac{1}{k}&=&\sum_{k=1}^{2^t}\frac{1}{k}+\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k} \\
&\geq& 1+\frac{t}{2}+\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k}
\end{eqnarray}
従って、\(t\geq 1\)で
$$\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k}\geq \frac{1}{2}$$
が成り立てば良いことになる。
\begin{eqnarray}
\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k}&=&\frac{1}{2^t+1}+\frac{1}{2^t+2}+\dots +\frac{1}{2^{t+1}} \\
&=&\frac{1}{2^t+1}+\frac{1}{2^t+2}+\dots +\frac{1}{2^t+2^t} \\
\end{eqnarray}
ここで、任意の\(a\in\mathbb{N}\)に対して、\(2^a>a\)が成り立つ(「区間縮小法とアルキメデスの原理からデデキントの定理を証明しよう!」)ので、
\begin{eqnarray}
\frac{1}{2^t+1}+\frac{1}{2^t+2}+\dots +\frac{1}{2^t+2^t}&>&\frac{1}{2^t+2^t}+\frac{1}{2^t+2^t}+\dots +\frac{1}{2^t+2^t} \\
&=&\frac{1}{2^t+2^t}\cdot 2^t=\frac{1}{2}
\end{eqnarray}
従って、\(t\geq 1\)で
$$\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k}\geq \frac{1}{2}$$
が成り立つので、
$$\sum_{k=1}^{2^{t+1}}\frac{1}{k}\geq 1+\frac{t+1}{2}$$
が成り立つ。
(Q.E.D.)
(ステップ2)
今、\(\displaystyle b_m=1+\frac{m}{2}\)で定められる新たな数列\(\{b_m\}_{m\in\mathbb{N}}\)が得られた。
ステップ2としてこの数列が\(\infty\)に発散することを示す。
これは殆ど例1.の証明と同じであるので、ぜひ証明に挑戦してもらいたい。
(補題5.の証明)
示したいことは、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ \left(\forall n\in\mathbb{N}\ m\geq N\Rightarrow 1+\frac{m}{2}>U\right)$$
である。
すなわち、任意の実数\(U\)に対して、上記を満たすような番号\(N\)を見つけてくれば良い。
アルキメデスの原理から、
$$(\forall a\in\mathbb{R}_{>0})(\forall b\in\mathbb{R}{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ b<N_0a$$
が成り立つ。
従って、\(a=1,\ b=2(|U|+1)\)としても成り立つ。
故に\(\displaystyle |U|+1<\frac{N_0}{2}\)という\(N_0\)を見つけてくることができる。 \(N\)として\(N_0\)を採用すると、任意の\(m\geq N\)なる自然数\(m\)に対して、
$$b_m=1+\frac{m}{2}>\frac{m}{2}\geq\frac{N}{2}>|U|+1>U$$
が成り立つ。
従って、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall m\in\mathbb{N}\ m\geq N\Rightarrow b_m>U)$$
が成り立ったので、\(\displaystyle \lim_{n\to\infty}\left(1+\frac{m}{2}\right)=\infty\)である。
(Q.E.D.)
(ステップ3)
次に追い出しの原理を述べる。
一言で言えば、発散する数列よりも大きい値を取る数列も発散する、ということである。
(補題6.の証明)
\(\displaystyle \lim_{n\to\infty}a_n=\infty\)であるので、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow a_n>U)$$
が成り立っている。
今、\(a_n\leq b_n\)であるのだから、
$$b_n\geq a_n>U$$
が成り立つ。
すなわち、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow b_n>U)$$
が成り立っているので、\(\displaystyle \lim_{n\to\infty}b_n=\infty\)である。
(Q.E.D.)
では(ステップ3)の証明に戻る。
今までのことをまとめれば、
$$\sum_{k=1}^{n}\frac{1}{k}>\sum_{k=1}^{2^m}\frac{1}{k}>1+\frac{m}{2}$$
であり、かつ
$$\lim_{m\to\infty}\left(1+\frac{m}{2}\right)=\infty$$
である。
従って、追い出しの原理から、
$$\lim_{m\to\infty}\sum_{k=1}^{2^m}\frac{1}{k}=\infty$$
が成り立つ。
さらに、\(n\geq2^m\)なのだから、\(m\)が限りなく大きくなるとき(つまり、\(m\to\infty\)のとき)、\(n\to\infty\)である。
従って、再度追い出しの原理により、
$$\lim_{n\to\infty}\sum_{k=1}^{n}\frac{1}{k}=\infty$$
である。
(Q.E.D.)
例3.について
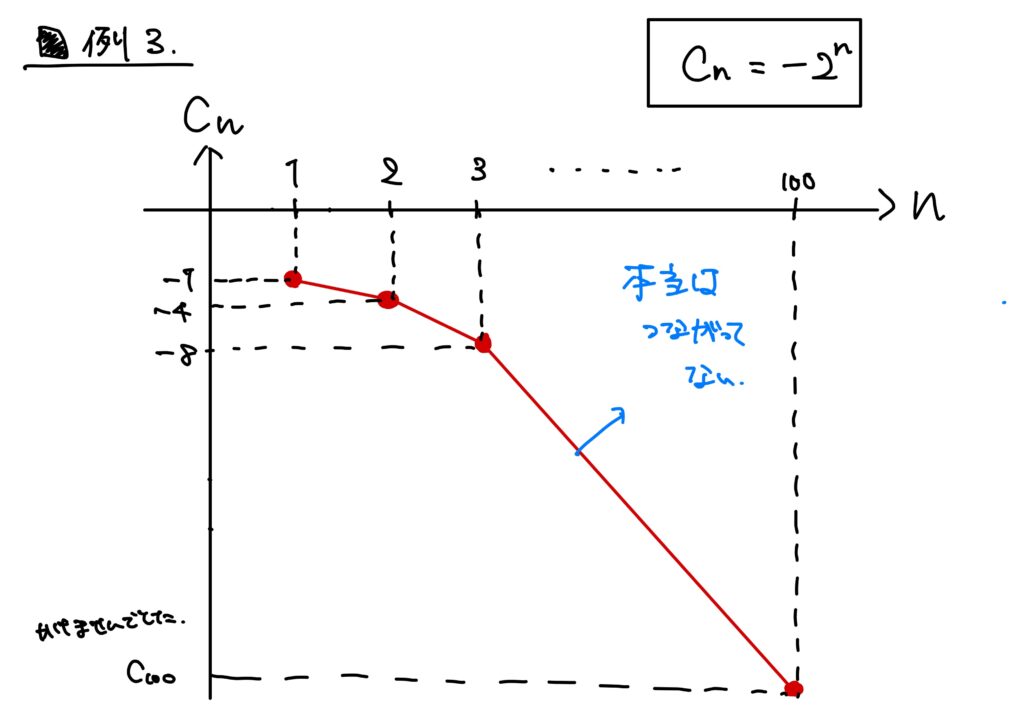
この証明も至って難しいわけではない。
例1.の証明が理解できていれば何ら問題ではない。
故に、この証明もぜひ挑戦してみてほしい。
(証明)
示したいことは、
$$(\forall L\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow -2^n<L)$$
である。
すなわち、任意の実数\(L\)に対して、上記を満たすような番号\(N\)を見つけてくれば良い。
アルキメデスの原理から、
$$(\forall a\in\mathbb{R}_{>0})(\forall b\in\mathbb{R}_{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ b<N_0a$$
が成り立つ。
従って、\(a=1,\ b=|L|+1\)としても成り立つ。
故に\(-|L|-1<-N_0\)という\(N_0\)を見つけてくることができる。 さらに、任意の自然数に対して、\(2^n>n\)が成り立つ(「区間縮小法とアルキメデスの原理からデデキントの定理を証明しよう!」を参照)。
以上のことを踏まえて、\(N\)として\(N_0\)を採用すると、任意の\(n\geq N\)なる自然数\(n\)に対して、
$$-2^n<-n\leq -N<-|L|-1<L$$
が成り立つ。
従って、
$$(\forall L\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow -2^n<L)$$
が成り立ったので、\(\displaystyle \lim_{n\to\infty}(-2^n)=-\infty\)である。
(Q.E.D.)
結
今回は数列が発散することを実際に証明してみた。
勘所としては数列の収束と同じで、「もしこんな番号\(N\)があったら…」という発想で論を展開してく。
次回は関数の極限について説明する。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!




コメントをする