本記事の内容
本記事はワイエルシュトラスの最大値定理の証明を与える記事です。
本記事を読むにあたり、関数の連続性とボルツァーノ-ワイエルシュトラスの定理を知っている必要があるため、その際は以下の記事を参照してください。
↓関数の連続性の記事
↓ボルツァーノ-ワイエルシュトラスの定理の記事
まずはイメージの復習から。
ワイエルシュトラスの最大値定理のイメージの復習
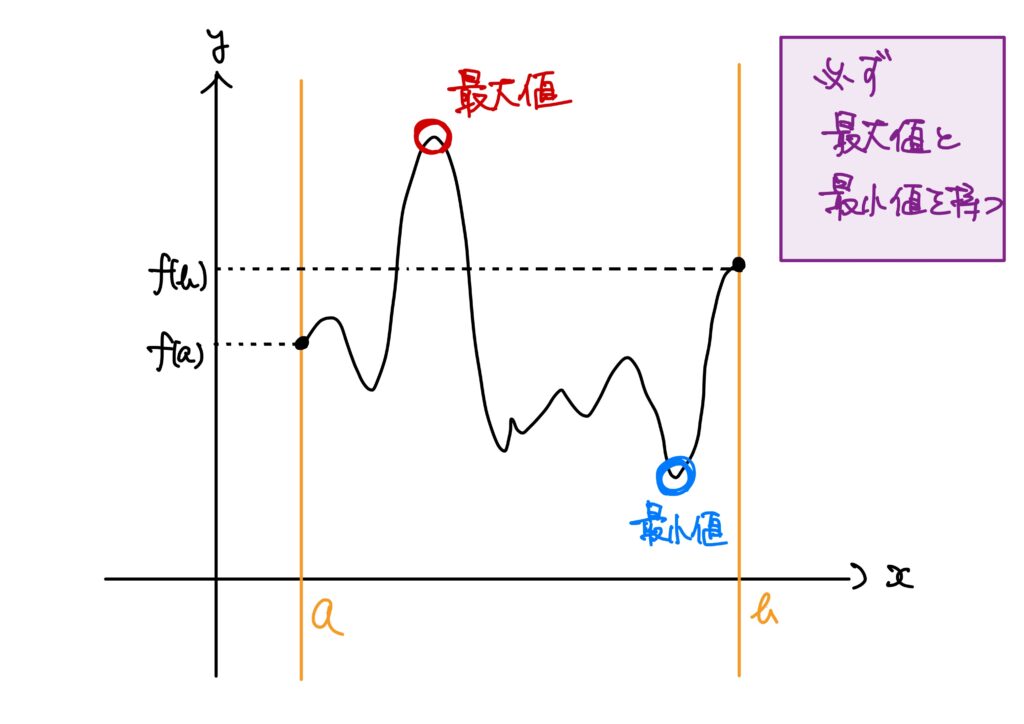
ワイエルシュトラスの最大値定理はどういうイメージだったかというと、
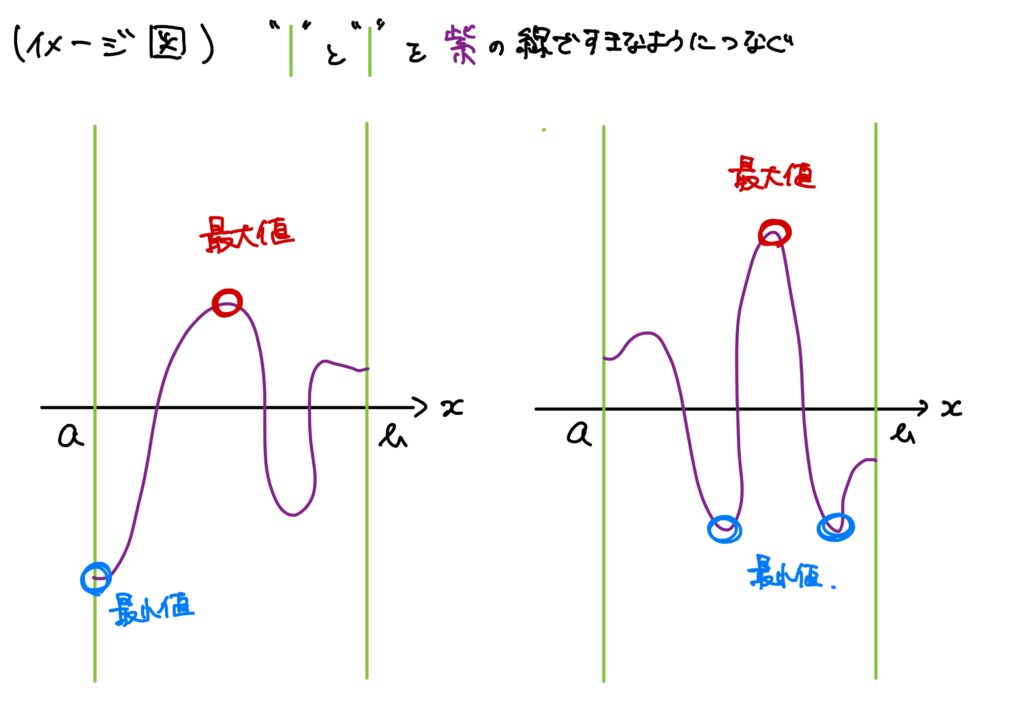
ということでした。
詳しくは【解析学の基礎シリーズ】関数の極限編 その15を参照してください。
では、ワイエルシュトラスの最大値定理は何か、ということを明示します。
ワイエルシュトラスの最大値定理の明示
証明をするための発想
筆者は最初にこの定理を知ったとき、「当たり前じゃね？」と思いました。
「そりゃあ閉区間で連続なら最大値も最小値もあるでしょうよ。」と思いました。
また同時に「どうすんだよ」とも思いました。
最大値と最小値のそれぞれの証明は殆ど同じだろう、という予想のもと(あくまで予想です)まずは最大値について考えてみましょう。
示すことは、最大値が存在すること、つまりは、あるc∈Kが存在して、任意のx∈Kに対してf(x)≤f(c)ということです。
そもそも最大値が存在するためには、関数が上に有界でないといけません。
(上に有界でなければ最大値は存在しません。)
もし上に有界であれば、必ずその上限が存在します。
ということは、最大値の候補として今見つけた上限が挙げられます。
しかし、上限は必ずしも最大値とは一致しません(「上限と最大値、下限と最小値は違うの？」【解析学の基礎シリーズ】を参照)。
もしこの上限と最大値が一致していれば「最大値はさっき見つけた上限ですね。」ということで存在が証明されます。
というわけで、まずは関数が上に有界だ、ということを証明する必要があるな、と思えるわけです。
さて、上に有界だということが証明できたとして、どうやって上限が最大値と一致することを証明するのか、ということです。
今使える情報は関数が連続である、ということと上限が存在する、ということです。
「折角上限の存在が分かったし、上限の性質を使いたいなあ」と筆者は思います。
上限とは何だったかというと、
- SはAの上界である。すなわち、次が成り立つ。∀x∈A x≤S
- Sよりも小さい数はAの上界ではない。すなわち、次が成り立つ。 (∀ϵ>0)(∃x∈A) s.t. x>S−ϵ
でした。
詳しくは、「上に有界、上界、上限」「下に有界、下界、下限」【解析学の基礎シリーズ】を参照してください。
つまり、
(∀ϵ>0)(∃f(x)∈f(K)) s.t. S−ϵ<f(x)≤S
が成り立つ、ということです。
このϵ>0は任意の正数ですので、正数であれば何でもよいわけです。
従って、「ϵの部分を0に収束するような数列にして、極限を取ればfの極限とSがはさみうちの原理(「ボルツァーノ-ワイエルシュトラスの定理を証明しよう！」【解析学の基礎シリーズ】)から一致することがわかるんじゃね？」となったわけです。
つまり、
limn→∞(S−(n→∞で0に収束する数列))<limn→∞f(x)<limn→∞S
により、f(x)=Sを示そうという魂胆です。
しかしこれでは少々問題があります。
というのも、上限は必ずしもその集合に属していないからです。
つまり、「必ずしもsupA∈Aではない」ということです。
従って、極限の操作で徐々にfの値をSに近づける必要があります。
故に
limn→∞(S−(n→∞で0に収束する数列))<limn→∞f(xn)<limn→∞S
を考えたほうが良さそうです。
ここで、fが連続な関数だったことを思い出すと、
limn→∞f(xn)=f(limn→∞xn)
です。
さらに、このxnは全てのn∈Nでxn∈Kですから有界な数列です。
従って、ボルツァーノ-ワイエルシュトラスの定理から収束する部分列が取れます。
その収束先でのfの値こそ最大値ではなかろうか、と思えます。
最小値も同じです。
これはあくまで発想の原点ですので、大枠ですから厳密ではありません。
「この方針でやってみるか」程度のものです。
いざ、証明
証明の流れ
- (ステップ1)：f(K)が上に有界であることを示すために「閉区間で連続な関数はその閉区間で有界である。」ことを証明する。
故に、上限と下限が存在することが分かる。 - (ステップ2)：見つけてきた上限がf(K)の要素であることを示す。
上限がf(K)の要素であれば、その上限がf(K)の最大値である。 - (ステップ3)：見つけてきた下限がf(K)の要素であることを示す。
下限がf(K)の要素であれば、その下限がf(K)の最小値である。
ワイエルシュトラスの最大値定理の証明
(ステップ1)：f(K)が上に有界であることを示すために「閉区間で連続な関数はその閉区間で上に有界である。」ことを証明する。
まずは、「閉区間で連続な関数はその閉区間で上に有界である」ということを証明しましょう。
(証明の流れ)
- (補題1.の証明のステップ1)：仮に故に有界でないとする。
有界でないのだから、値が発散してしまう。
ということは極限が存在しない。
極限を絡ませるために部分列を用意する。 - (補題1.の証明のステップ2)：関数が連続である事実を使うと、実はその関数は収束してしまう。矛盾。
補題1.の証明
(補題1.の証明のステップ1)：仮に故に有界でないとする。
背理法で証明してみましょう。
仮に、f(K)が上に有界でないとします。
すると、任意の自然数nに対してf(xn)>nとなるようなxn∈Kが存在します。
K=[a,b]ですから、Kは有界な集合です。
従って、xn∈Kですから、数列{xn}n∈Nは上にも下にも有界な数列です。
故にボルツァーノ-ワイエルシュトラスの定理が使えます。
数列{xn}n∈Nが有界な数列ならば、その数列に対する収束する部分列が存在する。
従って、数列{xn}n∈Nは収束する部分列{xn(k)}k∈Nを含みます。
そこで、limk→∞xn(k)=αとします。
常にxn(k)∈K、すなわちa≤xn(k)≤bですから、limk→∞a≤limk→∞xn(k)≤limk→∞bです。
すなわち、
a≤α≤b
です。
fは連続ですから、limk→∞f(xn(k))=f(α)です(【解析学の基礎シリーズ】関数の極限編 その14)。
(補題1.の証明のステップ2)：関数が連続である事実を使うと、実はその関数は収束してしまう。
しかしながら、f(xn)>nによりf(xn(k))>n(k)です。
さらに、k→∞のとき、n(k)→∞です。
従って、f(xn)>nからlimn(k)→∞f(xn)>∞です。
これはlimk→∞f(xn(k))=f(α)に矛盾です。
下に有界であることも同じように証明できます。
下に有界であることは簡単に述べます。
背理法で示します。
仮に、f(K)が下に有界でないとします。
すると、任意の自然数nに対してf(yn)<nとなるようなyn∈Kが存在します。
K=[a,b]ですから、Kは有界な集合です。
従って、yn∈Kですから、数列{yn}n∈Nは上にも下にも有界な数列です。
故にボルツァーノ-ワイエルシュトラスの定理が使えます。
従って、数列{yn}n∈Nは収束する部分列{yn(k)}k∈Nを含みます。
そこで、limk→∞yn(k)=βとします。
常にyn(k)∈K、すなわちa≤yn(k)≤bですから、limk→∞a≤limk→∞yn(k)≤limk→∞bです。
すなわち、
a≤β≤b
です。
fは連続ですから、limk→∞f(yn(k))=f(β)です。
しかしながら、f(xn)<nによりf(yn(k))<n(k)です。
さらに、k→∞のとき、n(k)→∞です。
従って、f(yn)<nからlimn(k)→∞f(yn)<∞です。
これはlimk→∞f(yn(k))=f(β)に矛盾です。
補題1.の証明終わり
補題1.から閉区間で連続な関数は有界であることが分かりました。
従って、f(K)には上限S=supx∈Kf(x)が存在します。
(ステップ2):上限がf(K)の要素であることを示す。
次にこの上限が最大値であるということを示します。
ここで、上限は上界の中の最小の値でした。
従って、S=supx∈Kf(x)∈f(K)であることを示せば良いのです。
さて、Sはf(K)の上限ですので、
(∀ϵ>0)(∃xn∈K) s.t. S−ϵ<f(xn)≤S
が成り立ちます。
このϵは正の実数であれば何でも良いわけですので、任意のn∈Nに対して
(∃xn∈K) s.t. S−1n<f(xn)≤S
も成り立ちます。
実際、n∈nに対して1n>0です。
従って、この不等式の各辺に極限をとると、
limn→∞(S−1n)<limn→∞f(xn)≤limn→∞S
です。
従って、
limn→∞f(xn)=S
です。
ここで、ボルツァーノ-ワイエルシュトラスの定理から数列{xn}n∈Nの収束する部分列{xn(k)}k∈Nが存在します。
すなわち、
(∃c∈R) limk→∞xn(k)=c
です。
実は、c∈Kです。
実際、xn(k)∈Kですので、a≤xn(k)≤bですから、k→∞とすると、a≤limk→∞xn(k)≤bとなり、a≤c≤bです。
従って、c∈Kです。
fはKで連続ですので、c∈Kでも連続です。
従って、
f(limk→∞xn(k))=f(c)
ここで、もう一つの事実を使います。
数列{an}n∈Nがaに収束するならば、任意の部分列{an(k)}k∈Nはaに収束する。 つまり、収束列の部分列は同じ極限に収束する。
補題2.の証明
示したいことは
(∀ϵ>0)(∃N∈N)(∀k∈N:k≥N⇒|an(k)−a|<ϵ)
です。
今、{an}n∈Nがaに収束しているのだから、
(∀ϵ0>0)(∃N0∈N)(∀n∈N:n≥N⇒|an−a|<ϵ)
が成り立っています。
このとき、{an(k)}k∈Nは{an}n∈Nの部分列ですのでk≥Nを満たす任意のk∈Nに対して、n(k)≥k≥Nです。
実際、n(k+1)>n(k)により、n(k+1)≥n(k)+1であり、かつn(1)=1だからです。
故に、n(k)≥Nです。
ϵ0も任意の正の実数ですので、新たにϵと書き直すと、
(∀ϵ>0)(∃N∈N)(∀k∈N:k≥N⇒|an(k)−a|<ϵ)
が成り立ちました。
補題2.の証明終わり
では戻ります。
補題2.を使うと、
limn→∞xn=limk→∞xn(k)
が成り立ちます。
故に、
f(limn→∞xn)=f(limk→∞xn(k))
です。
以上のことから
f(c)=limk→∞f(xn(k))=S
が成り立ちます。
f(c)∈f(K)ですので、S∈f(K)です。
(ステップ3)：見つけてきた下限がf(K)の要素であることを示す。
最小値についても同じように証明できます。
補題1.から閉区間で連続な関数は有界であることが分かりました。
従って、f(K)には下限L=infx∈Kf(x)が存在します。
次にこの下限が最小値であるということを示します。
ここで、下限は下界の中の最大の値でした。
従って、L=infx∈Kf(x)∈f(K)であることを示せば良いのです。
さて、Lはf(K)の下限ですので、
(∀ϵ>0)(∃yn∈K) s.t. L−ϵ>f(yn)≥L
が成り立ちます。
このϵは正の実数であれば何でも良いわけですので、任意のn∈Nに対して
(∃yn∈K) s.t. L−1n>f(yn)≥L
も成り立ちます。
実際、n∈nに対して1n>0です。
従って、この不等式の各辺に極限をとると、
limn→∞(L−1n)>limn→∞f(yn)≥limn→∞L
です。
従って、
limn→∞f(yn)=L
です。
ここで、ボルツァーノ-ワイエルシュトラスの定理から数列{yn}n∈Nの収束する部分列{yn(k)}k∈Nが存在します。
すなわち、
(∃d∈R) limk→∞yn(k)=d
です。
実は、d∈Kです。
fはKで連続ですので、d∈Kでも連続です。
従って、
f(limk→∞yn(k))=f(d)
ここで、補題2.により
limn→∞yn=limk→∞yn(k)
が成り立ちます。
故に、
f(limn→∞yn)=f(limk→∞yn(k))
です。
以上のことから
f(d)=limk→∞f(yn(k))=L
が成り立ちます。
f(d)∈f(K)ですので、L∈f(K)です。
従って、ワイエルシュトラスの最大値定理が成り立ちます。
ワイエルシュトラスの最大値定理の証明終わり
ワイエルシュトラスの最大値定理の使いみち
この定理のつかいみちは色々ありますが、特に解析学では微積分で有効な場合が多いです。
というのも、ワイエルシュトラスの最大値定理は、ロルの定理の証明に用いられていて、ロルの定理を使って平均値の定理、それからテイラーの定理が導けます。
(「ふーん。そんな定理もあるんだ。」くらいでいいです。しかし実際学んでみるとどれも凄まじい定理です。)
ちなみに、高校数学でさも当たり前かのように使っている「ある区間でf′>0ならば、fは増加関数である。」という定理は平均値の定理を使って証明します。
従って、ワイエルシュトラスの最大値定理はそういう意味で基礎となる定理です。
結
今回はワイエルシュトラスの最大値定理の証明をしました。
証明の流れとしては、
- 閉区間で連続な関数は有界であることを示す。
- 従って上限と下限が存在する。
- その上限と下限がそれぞれ最大値、最小値であることを示す。
という割とシンプルな流れです。
しかし、実際使っているのはボルツァーノ-ワイエルシュトラスの定理だったりと、若干複雑です。
とはいえ、どういう発想で証明に至ったか、ということが少し分かれば納得がいくのではないでしょうか。
次回は「関数の発散」について解説します。
乞うご期待！質問、コメントなどお待ちしております！
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ１冊持っておくと良いと思います！
コメントをする