本記事の内容
本記事は、「正二十面体群は5次交代群と同型」という主張の証明を完結させる記事です。
本記事を読むに当たり、交代群と正多面体群について知っている必要があるため、以下の記事も合わせてご覧ください。
↓交代群の記事
↓正多面体群の記事
前回と今回で証明すること
今回と次回で証明することは以下です。
定理0.
\({\rm I}同型 A_5\)である。すなわち、正二十面体群は5次の交代群と同型である。\(n\)次交代群は\(n\)次対称群(置換群)の偶置換のみを集めた集合とも言えますので、この主張は「正二十面体の頂点を他の頂点に写す変換(写像)は、5次の偶置換である」とも言えます。
軽い復習
交代群
一言で述べれば、
です。
\(\sigma\)を置換とし、\({\rm sgn}(\sigma)\)を\(\sigma\)の符号とすると、\({\rm sgn}\)は\(\mathcal{G}_n\)から\(\left\{\pm1\right\}\)への準同型写像となります。
\(A_n={\rm Ker}({\rm sgn})\)(準同型写像\(\varphi\)の核\({\rm Ker}(\varphi)\)は正規部分群でしたね)と書き、\(A_n\)のことを\(n\)次交代群といいます。
正多面体群
正多面体群を一言で表すと、
です。
ここで注意なのが、正多面体群の要素は正多面体ではないということです。
筆者だけかも知れませんが「正多面体群」という字面を見ると「正多面体自体が群になるのかな?」と思うかもしれません。
しかし違います。
あくまで正多面体をその同じ正多面体に写すような変換(写像)が要素です。
正多面体群
正多面体\(\mathcal{P}_i\ (i=4,6,8,12,20)\)に対して、- 合同変換 \(\mathcal{P}_i\)を\(\mathbb{R}^3\)内の単位球面に内接させる。このとき原点を中心とする回転のうち、頂点を頂点に写すものを\(\mathcal{P}_i\)の合同変換という。
- 正多面体群 \(\mathcal{P}_i\)の合同変換\(\sigma\)の逆回転\(\sigma^{-1}\)もまた合同変換であり、合同変換\(\sigma,\tau\)を続けて行った変換(\(\tau\sigma\)と書く)もまた合同変換である。故に合同変換全体は、変換の合成(写像の合成)を演算として群をなす。この群を正\(i\)面体群という。また、正二面体群と合わせてこれらをまとめて正多面体群という。
正八面体の各辺の中点を結ぶと立方体になります。
また、正二十面体の各辺の中点を結ぶと正十二面体になります。
したがって、正八面体群と立方体群は同型で、正二十面体群と正十二面体群は同型です。
正四面体群、正八面体群、正二十面体群をそれぞれ\({\rm T},\ {\rm O},\ {\rm I}\)(tetrahedron、octahedron、icosahedronの頭文字)と書きます。
詳しくは、【代数学の基礎シリーズ】群論編 その44を御覧ください。
定理0.の証明の流れ
定理0.の証明の流れは以下です。
- \({\rm I}\)を正十二面体群とみなして、頂点に着目して立方体を作り、立方体の頂点を回転させて頂点の対応を観察する(巡回置換)。→【代数学の基礎シリーズ】群論編 その48で証明済み。
- \(A_5\)がある置換で生成されることを示し、同型写像が存在することを示す。→今回
いざ、証明
まずは、ひとつ補題を証明します。
補題1.
5次交代群\(A_5\)は\((1\ 2\ 3\ 4\ 5)\)および\((2\ 5\ 4)\)で生成される。補題1.を証明する前に、生成された部分群を軽く復習します。
語、生成された部分群、生成系、生成元
- 語 \(G\)を群、\(S\subset G\)とする。\(x_1,\dots,x_n\in S\)により\(x_1^{\pm1}\cdots x_n^{\pm1}\)という形をした\(G\)の要素を\(S\)の要素による語(word)という。
- 生成された部分群 \(\langle S\rangle\)を\(S\)の要素による語全体の集合とするとき、\(\langle S\rangle\)を\(S\)によって生成された部分群、\(S\)のことを生成系、\(S\)の要素を生成元という。
ただし、\(n=1\)ならば\(x_1^{\pm1}\cdots x_n^{\pm1}\)は単位元\(1_G\)を表すとし、\(\pm1\)は各\(x_i\)ごとに\(1\)か\(-1\)のどちらでも良いとする。
詳しくは、【代数学の基礎シリーズ】群論編 その2を御覧ください。
補題1.の証明
まず、\((1\ 2\ 3\ 4\ 5),(2\ 5\ 4)\in A_5\)です。
\(H\)をこれらの要素で生成された\(A_5\)の部分軍とします。
\((1\ 2\ 3\ 4\ 5)^i(2\ 5\ 4)(1\ 2\ 3\ 4\ 5)^{-i}\ (i=0,1,2,3,4)\)よう置換を考えます。
すると、
$$
(2\ 5\ 4),\ (3\ 1\ 5),\ (4\ 2\ 1),\ (5\ 3\ 2),\ (1\ 4\ 3)\in H
$$
であることが分かります。
$$
(2\ 5\ 4)(4\ 2\ 1)=(1\ 2)(4\ 5),\quad (2\ 5\ 4)(1\ 2)(4\ 5)(2\ 5\ 4)^{-1}=(1\ 5)(2\ 4)\in H
$$
であるから、\(H\)は\(\left\langle (1\ 2)(4\ 5),(1\ 5)(2\ 4)\right\rangle\cong\mathbb{Z}/{2\mathbb{Z}}\times\mathbb{Z}/{2\mathbb{Z}}\)を含みます。
故に、\(\left|H\right|\)は\(3,4,5\)で割り切れ、\(\left|H\right|\geq60\)です。
\(H\subset A_5\)だから、\(H=A_5\)です。
補題1.の証明終わり
では、定理0.の証明を完結させます。
定理0.の証明の続き
前回の証明(【代数学の基礎シリーズ】群論編 その48)の続きです。
まず、記号のお話から。
正十二面体の頂点に、以下の図のように番号をつけて、\({\rm P}_1,\cdots,{\rm P}_{20}\)とします。

\(C_1,\cdots,C_5\)を次の集合を頂点の集合とする多面体とします。
\begin{eqnarray}
&&C_1:\left\{{\rm P}_1,{\rm P}_4,{\rm P}_6,{\rm P}_9,{\rm P}_{11},{\rm P}_{14},{\rm P}_{17},{\rm P}_{19}\right\}\\
&&C_2:\left\{{\rm P}_2,{\rm P}_5,{\rm P}_6,{\rm P}_8,{\rm P}_{11},{\rm P}_{13},{\rm P}_{18},{\rm P}_{20}\right\}\\
&&C_3:\left\{{\rm P}_1,{\rm P}_3,{\rm P}_8,{\rm P}_{10},{\rm P}_{13},{\rm P}_{15},{\rm P}_{16},{\rm P}_{19}\right\}\\
&&C_4:\left\{{\rm P}_2,{\rm P}_4,{\rm P}_7,{\rm P}_{10},{\rm P}_{12},{\rm P}_{15},{\rm P}_{17},{\rm P}_{20}\right\}\\
&&C_5:\left\{{\rm P}_3,{\rm P}_5,{\rm P}_7,{\rm P}_9,{\rm P}_{12},{\rm P}_{14},{\rm P}_{16},{\rm P}_{18}\right\}
\end{eqnarray}
\(C_1\)は以下の図のように、正十二面体に内接する立方体です。
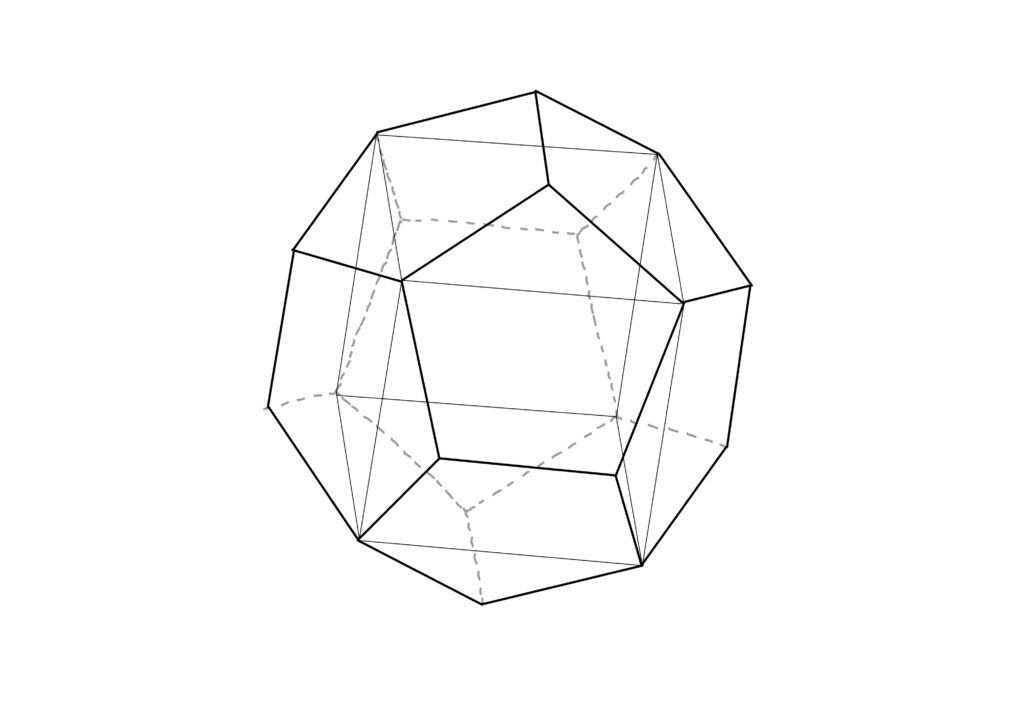
さて、\(K\subset{\rm I}\)(正二十面体群が正十二面体群と同型であることから、\({\rm I}\)を正十二面体として捉えたのでした)を\(\sigma,\tau\)で生成された\({\rm I}\)の部分群とします。
\(\sigma,\tau\)は集合\(X=\left\{C_1,\cdots,C_5\right\}\)を不変にしますので、\(K\)は\(X\)に作用しています。
ここで、群作用とは以下でした。
群作用
\(G\)を群、\(X\)を集合とする。\(G\)の\(X\)への左作用とは、写像\(\varphi:G\times X\ni (g,x)\mapsto \varphi(g,x)\in X\)であり、次の性質1.、2.を満たすものをいう。- \(\varphi(1_G,x)=x\)
- \(\varphi(g,\varphi(h,x))=\varphi(gh,x)\)
- \(\varphi(1_G,x)=x\)
- \(g(hx)=xgh)\)
\(G\)の\(X\)への作用が存在するとき、\(G\)は\(X\)に作用するという。左作用なら、\(G\)は\(X\)に左から作用するという。右作用も同様である。
詳しくは、【代数学の基礎シリーズ】群論編 その11を御覧ください。
この作用により定まる置換表現(直下で復習します)を\(\rho:K\longrightarrow \mathcal{G}_5\)(\(\mathcal{G}_5\)は\(5\)次の対称群で、直下で復習します)とします。
ここで、作用により定まる置換表現とは以下でした。
置換表現
群\(G\)が有限集合\(X=\left\{x_1,\dots,x_n\right\}\)に左から作用するとする。このとき $$ g\cdot x_i=x_{\rho(g)(i)}\quad (g\in G,\ i=1,\dots,n) $$ として定めると、\(\rho:G\longrightarrow \mathcal{G}_n\)は準同型写像である。この\(\rho\)を\(X\)への作用により定まる置換表現という。詳しくは、【代数学の基礎シリーズ】群論編 その13を御覧ください。
また、対称群とは以下でした。
は写像の合成を演算として群でした。
この\(\mathcal{G}_X\)は特別な呼び名があり、置換群、または対称群と呼びます。
これは、まさに以前線型代数の記事で解説した置換が、写像の合成でもって群であるということです。
置換とは以下でした。
置換
\(n\in\mathbb{N}\)とする。\(n\)個の文字\(1,2,\dots,n\)からなる集合を $$ M_n=\{1,2,\dots,n\} $$ とする。写像\(\sigma:M_n\to M_n\)が全単射であるとき、\(\sigma\)を\(M_n\)の置換という。置換\(\sigma\)による対応が $$ 1\mapsto i_1,\ 2\mapsto i_2,\dots,n\mapsto i_n $$ であるとする、すなわち、 $$ \sigma(1)=i_1,\ \sigma(2)=i_2,\dots,\ \sigma(n)=i_n $$ とする。このとき\(\sigma\)を $$ \sigma= \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix} $$ と書く。
詳しくは【線型代数学の基礎シリーズ】行列式編 その1を御覧ください。
\(X=M_n\)のとき、\(\mathcal{G}_X\)を\(\mathcal{G}_n\)と書きます。
さて、\(\rho:K\longrightarrow \mathcal{G}_5\)に対して\(\rho(\sigma)=(1\ 2\ 3\ 4\ 5)\)、\(\rho(\tau)=(2\ 5\ 4)\)なので、補題1.により\(\rho(K)\supset A_5\)です。
\(\left|K\right|\leq \left|{\rm I}\right|=60=\left|A_5\right|\)だから、\(K={\rm I}\)であり、\(\rho\)は\(I\)から\(A_5\)への同型写像となります。
定理0.の証明終わり
ちなみに、この証明から、\({\rm I}\)は\(X\)を不変にすることも分かりました。
実際には正十二面体に内接する頂点を共有する立方体は、前回示した立方体だけだということが分かります。
皆様のコメントを下さい!
今回も背理法とそれに付随していることをお話します。
前回は、間違った否定命題を与えて、それが間違いであることを例とともに述べました。
その例が以下です。
この「ある人」が行った議論には間違いがあります。
最初の部分は正しい。間違いは、後半で「クレタ人は嘘吐きである」の否定を「クレタ人は正直である」としたところにある。これを見るには、「クレタ人は嘘吐きである」の、より正確な表現「すべてのクレタ人は嘘吐きである」を考えればよい。この否定は「ある(少なくとも一人の)クレタ人は嘘吐きでない(すなわち正直である)」となって、エピメニデスが、この正直なクレタ人かどうかは分からない。従って矛盾は生じない。
さて、この単純な例から学ぶべきことは、2つあります。
- 我々が日常話したり書いたりする文章には曖昧さがあることです。
もし論理的に正確を期そうとすれば、文章を分析し、それが意味することを明確にしなければなりません。
特に数学的な文章の場合これは重要なことです。 - 技術的問題ですが、文章の否定形を考えたときに「ある · · · 」と「すべての · · · 」が入れ替 わることです。
背理法の英語名である「proof by contradiction」における「contradiction」に対応する「矛盾」と いう言葉は、韓非(Han Fei;紀元前?-233)が書いた「韓非子」の中に出てくる逸話に由来しています。
掻い摘んで言えば、これは、どんな矛でも突き通せない楯と、どんな楯も突き通す矛の両方を売るという武器商人が、「お前の持っているという矛で楯を突いたらどうなる?」と問われて答えに窮したという話です。
韓非(前280?–前233年)は中国の戦国時代末期の思想家です。
その生涯は司馬遷の『史記』「老子韓非子列伝第三」および「李斯伝」で簡単に触れられています。
秦王が韓非を登用しようと考えましたが、ときの宰相であった李斯は韓非の才能が自分の地位を脅かすことを恐れて王に讒言。
このため韓非は牢につながれ、獄中、李斯が毒薬を届けて自殺を促し、韓非はこれに従ったそうです。
韓非は「人間は元来悪であって、個人的快楽と富を追及する傾向がある」としました(性悪説)。
それは孔子を始祖とする儒家の考え方とはまったく逆です。
韓非の思想(法家)は、秦の始皇帝による中国統一の理論的支柱となりました。
今回はここまで。
感想など是非コメントを下さい!
結
今回は、「正二十面体群は5次の交代群と同型である。」という主張の証明を完結させました。
正十二面体群の部分集合を考えると、正十二面体の面の集合に作用してます。
この作用による置換表現が全単射準同型(つまりは同型)写像であることを示す、という流れです。
次回からは流れが逆行しているようですが、初等整数論の話をします。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。





コメントをする
細かいことですが、
>この主張は「正二十面体の頂点を他の頂点に写す変換(写像)は、4次の偶置換である」とも言えます。
についてですが、「5次の偶置換」だと思います。
田淵隆明さま
コメントありがとうございます。
>細かいことですが、
>>この主張は「正二十面体の頂点を他の頂点に写す変換(写像)は、4次の偶置換である」とも言えます。
>についてですが、「5次の偶置換」だと思います。
とのお問い合わせですが、おっしゃる通りでございます。
訂正いたしました。
ご指摘ありがとうございました。