「正二十面体群は5次交代群と同型①」【代数学の基礎シリーズ】群論編 その48

本記事の内容

本記事は、「正二十面体群は5次交代群と同型」という主張の一部を解説する記事です。

本記事を読むに当たり、交代群と正多面体群について知っている必要があるため、以下の記事も合わせてご覧ください。

↓交代群の記事

「位数が12の群の分類①」【代数学の基礎シリーズ】群論編 その32

...

for-spring.com

2022.11.30

↓正多面体群の記事

「なぜ正多面体は5つだけなのか？」「正多面体群とは？」【代数学の基礎シリーズ】群論編 その44

...

for-spring.com

2022.12.19

今回と次回で証明すること

今回と次回で証明することは以下です。

$n$次交代群は$n$次対称群(置換群)の偶置換のみを集めた集合とも言えますので、この主張は「正二十面体の頂点を他の頂点に写す変換(写像)は、4次の偶置換である」とも言えます。

軽い復習

交代群

一言で述べれば、

です。
$\sigma$を置換とし、${\rm sgn}(\sigma)$を$\sigma$の符号とすると、${\rm sgn}$は$\mathcal{G}_n$から$\left\{\pm1\right\}$への準同型写像となります。
$A_n={\rm Ker}({\rm sgn})$(準同型写像$\varphi$の核${\rm Ker}(\varphi)$は正規部分群でしたね)と書き、$A_n$のことを$n$次交代群といいます。

正多面体群

正多面体群を一言で表すと、

です。
ここで注意なのが、正多面体群の要素は正多面体ではないということです。
筆者だけかも知れませんが「正多面体群」という字面を見ると「正多面体自体が群になるのかな？」と思うかもしれません。
しかし違います。
あくまで正多面体をその同じ正多面体に写すような変換(写像)が要素です。

正八面体の各辺の中点を結ぶと立方体になります。
また、正二十面体の各辺の中点を結ぶと正十二面体になります。
したがって、正八面体群と立方体群は同型で、正二十面体群と正十二面体群は同型です。
正四面体群、正八面体群、正二十面体群をそれぞれ${\rm T},\ {\rm O},\ {\rm I}$(tetrahedron、octahedron、icosahedronの頭文字)と書きます。

詳しくは、【代数学の基礎シリーズ】群論編 その44を御覧ください。

定理0.の証明の流れ

定理0.の証明の流れは以下です。

1. ${\rm I}$を正十二面体群とみなして、頂点に着目して立方体を作り、立方体の頂点を回転させて頂点の対応を観察する(巡回置換)。→今回
2. $A_5$がある置換で生成されることを示し、同型写像が存在することを示す。→次回

いざ、証明

正二十面体の各辺の中点を結ぶと正十二面体になることから、正十二面体群${\rm I}$と正十二面体群は同型です。
そこで、${\rm I}$を正十二面体群とみなします。
正十二面体の頂点に、以下の図のように番号をつけて、${\rm P}_1,\cdots,{\rm P}_{20}$とします。

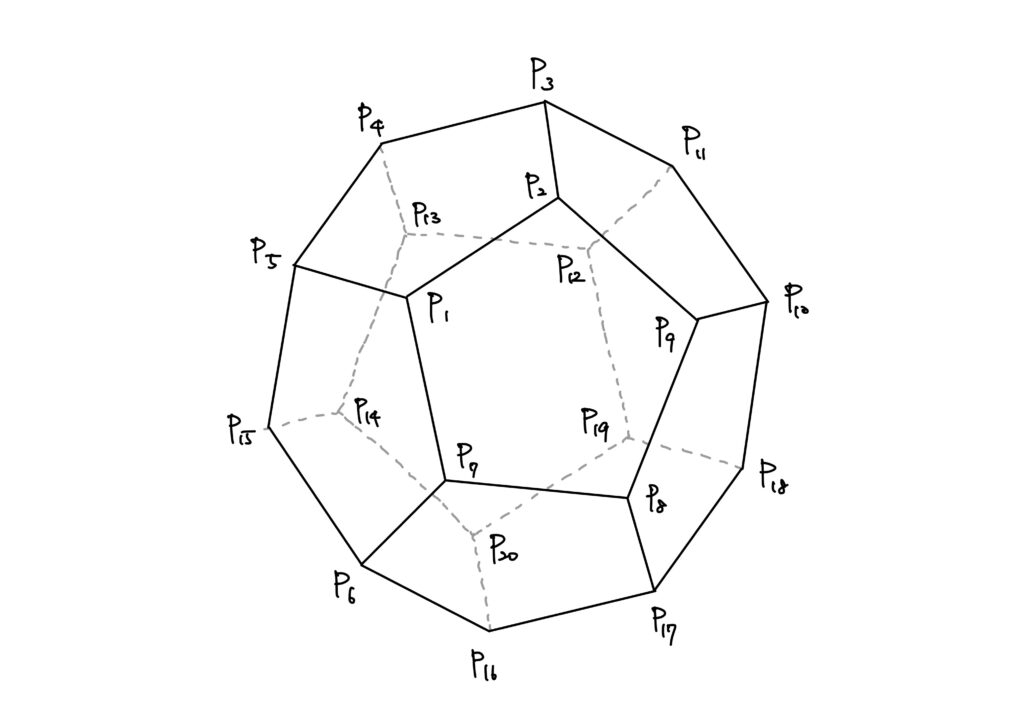
$C_1,\cdots,C_5$を次の集合を頂点の集合とする多面体とします。
$$\begin{eqnarray} &&C_1:\left\{{\rm P}_1,{\rm P}_4,{\rm P}_6,{\rm P}_9,{\rm P}_{11},{\rm P}_{14},{\rm P}_{17},{\rm P}_{19}\right\}\\ &&C_2:\left\{{\rm P}_2,{\rm P}_5,{\rm P}_6,{\rm P}_8,{\rm P}_{11},{\rm P}_{13},{\rm P}_{18},{\rm P}_{20}\right\}\\ &&C_3:\left\{{\rm P}_1,{\rm P}_3,{\rm P}_8,{\rm P}_{10},{\rm P}_{13},{\rm P}_{15},{\rm P}_{16},{\rm P}_{19}\right\}\\ &&C_4:\left\{{\rm P}_2,{\rm P}_4,{\rm P}_7,{\rm P}_{10},{\rm P}_{12},{\rm P}_{15},{\rm P}_{17},{\rm P}_{20}\right\}\\ &&C_5:\left\{{\rm P}_3,{\rm P}_5,{\rm P}_7,{\rm P}_9,{\rm P}_{12},{\rm P}_{14},{\rm P}_{16},{\rm P}_{18}\right\} \end{eqnarray}$$
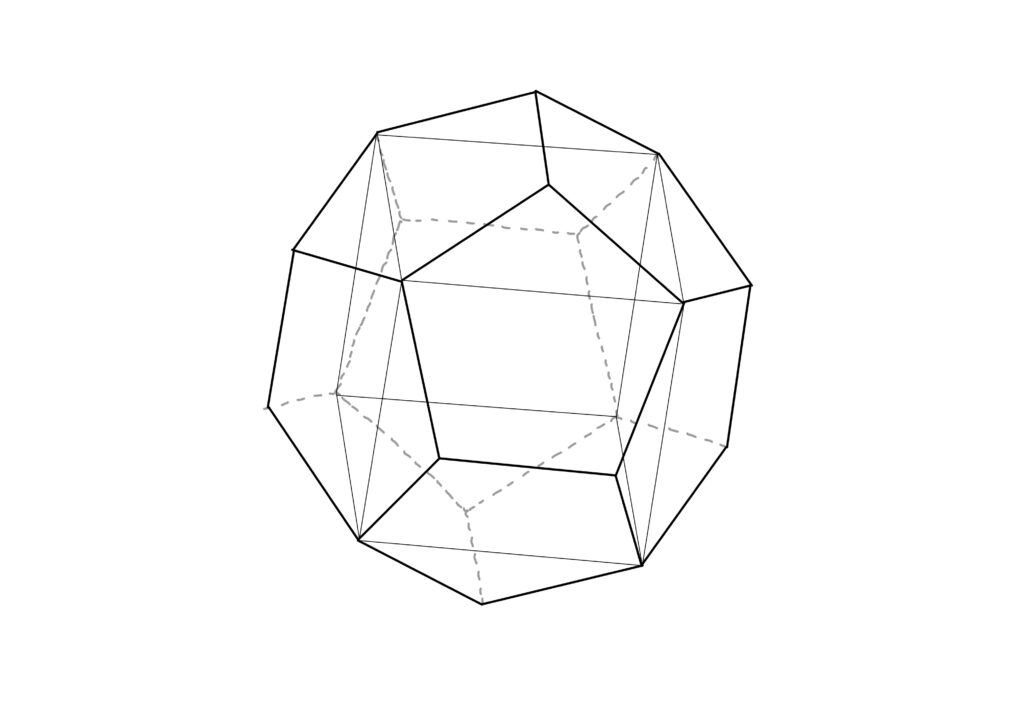
$C_1$は以下の図のように、正十二面体に内接する立方体です。

${\rm P}_1,{\rm P}_2,{\rm P}_3,{\rm P}_4,{\rm P}_5$の面を、この面の外側から見て反時計回りに$\displaystyle\frac{2\pi}{5}$だけ回転させる${\rm I}$の要素を$\sigma$とすれば、頂点は
$$\begin{eqnarray} &&{\rm P}_1\longrightarrow{\rm P}_2\longrightarrow{\rm P}_3\longrightarrow{\rm P}_4\longrightarrow{\rm P}_5\longrightarrow{\rm P}_1\\ &&{\rm P}_6\longrightarrow{\rm P}_8\longrightarrow{\rm P}_{10}\longrightarrow{\rm P}_{12}\longrightarrow{\rm P}_{14}\longrightarrow{\rm P}_6\\ &&{\rm P}_7\longrightarrow{\rm P}_9\longrightarrow{\rm P}_{11}\longrightarrow{\rm P}_{13}\longrightarrow{\rm P}_{15}\longrightarrow{\rm P}_7\\ &&{\rm P}_{16}\longrightarrow{\rm P}_{17}\longrightarrow{\rm P}_{18}\longrightarrow{\rm P}_{19}\longrightarrow{\rm P}_{20}\longrightarrow{\rm P}_{16}\\ \end{eqnarray}$$
と移り合うことが分かります。
これにより、$C_1,\cdots,C_5$は
$$C_1\longrightarrow C_2\longrightarrow C_3\longrightarrow C_4\longrightarrow C_5\longrightarrow C_1$$
とう釣り合います。
したがって、$C_2,\cdots,C_5$も正十二面体に内接する立方体です。

また、頂点${\rm P}_1$に関する$\displaystyle\frac{2\pi}{3}$の回転により、頂点は
$$\begin{eqnarray} &&{\rm P}_1\longrightarrow {\rm P}_1,\quad {\rm P}_{19}\longrightarrow {\rm P}_{19},\\ &&{\rm P}_2\longrightarrow {\rm P}_5\longrightarrow {\rm P}_7\longrightarrow {\rm P}_2,\quad {\rm P}_3\longrightarrow {\rm P}_{15}\longrightarrow {\rm P}_8\longrightarrow {\rm P}_3,\\ &&{\rm P}_4\longrightarrow {\rm P}_6\longrightarrow {\rm P}_9\longrightarrow {\rm P}_4,\quad {\rm P}_{10}\longrightarrow {\rm P}_{13}\longrightarrow {\rm P}_{16}\longrightarrow {\rm P}_{10},\\ &&{\rm P}_{11}\longrightarrow {\rm P}_{14}\longrightarrow {\rm P}_{17}\longrightarrow {\rm P}_{11},\quad {\rm P}_{12}\longrightarrow {\rm P}_{20}\longrightarrow {\rm P}_{18}\longrightarrow {\rm P}_{12} \end{eqnarray}$$
と移り合います。

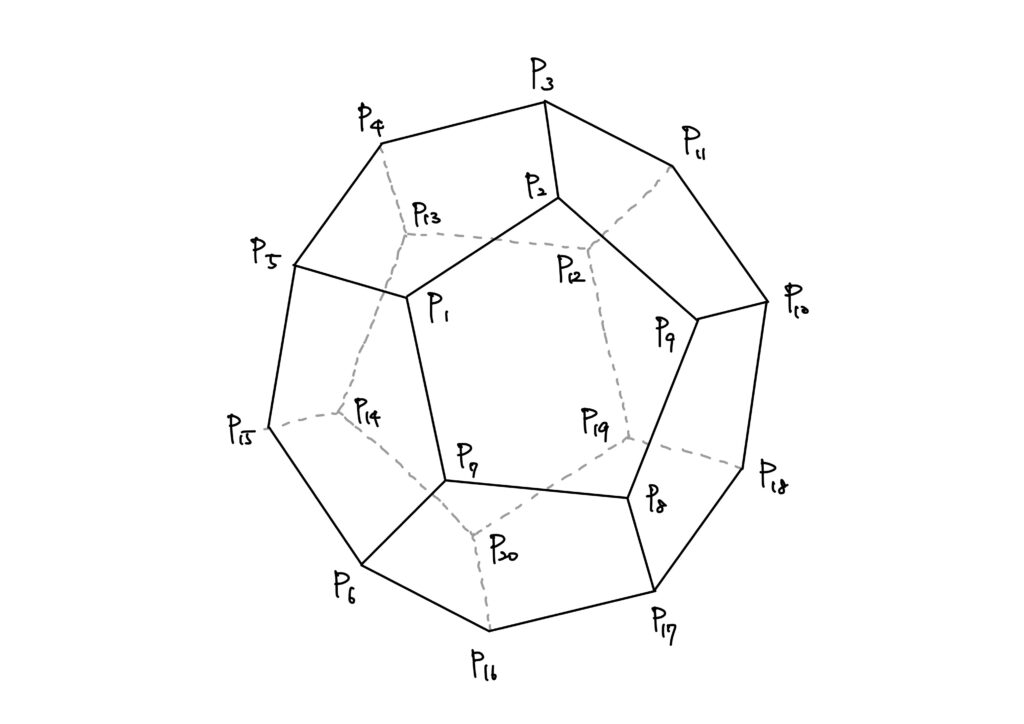
この回転を$\tau$とおけば、$\tau$により
$$C_1\longrightarrow C_1,\quad C_2\longrightarrow C_5\longrightarrow C_4\longrightarrow C_2,\quad C_3\longrightarrow C_3$$
と移り合うことが分かります。

今回はここまでです。

皆様のコメントを下さい！

背理法に付随して、否定命題について少々語ります。

真か偽かを判定できるような主張のことを命題といったのでした(【論理と集合シリーズ】その1)。

任意の命題を考えたとき、その内容を否定した命題(否定命題)を考えることができます。
そして命題が真であれば、その否定命題は偽であり、命題が偽であれば、その否定命題は真でした。
そして、与えられた命題とその否定命題のどちらか一方が常に真と考えるのが、数学者が取る通常の立場です。
これを排中律(Law of excluded middle)といいます。
排中律はパルメニデスにより初めて認識されたと言われています。

数学の本や論文では、補題、命題、定理という形で真であることが確かめられた数学的言明が述べられますが、論理学の中で「命題」というときはそれが真である必要はありません。

無制限に排中律の使用を認めない立場を取る数学者、いわゆる直観主義者という方がいるようです。
しかしほとんどの数学者は排中律を認めています。

背理法では与えられた主張(命題)の否定の内容を明確にする必要があります。
例えば「君は透明人間になれない」という主張の否定は単に「君は透明人間になれる」です。
しかし、もっと込み入った 文章に対しては余程心しないと間違った否定形を与えてしまいかねません。
また簡単な文章でも、その内容をよく吟味しないと正しい否定形を得られないこともあります。

代表例を紹介します。

クレタは地中海に浮かぶ島です。
ミノア文明(紀元前2000-1600)が花開いた所として知られています。
新約聖書「テトスへの手紙」の第1章の中で、クレタの預言者が言ったことが引用されています
「クレタ人は、いつもうそつき、たちの悪いけもの、なまけ者の食いしんぼう」。

この預言者が紀元前500年頃にクレタにいた賢人で詩人のエピメニデスです。
ディオゲネス・ラエルティオスの「ギリシャ哲学者列伝」には、エピメニデスについて簡単な解説があります。
それによれば、57年間眠り続け、157歳あるいは299歳で亡くなったそうです。
日本の「浦島伝説」やアーヴィングの小説“Rip Van Winkle”を思い起こさせる話でしょう。
プラトンやアリストテレスもエピメニデスに言及しています。

さて、「ある人」が行った議論には間違いがあります。
それを見つけてみて下さい。

今回はここまでです。
感想など是非コメントをお願いします！

結

今回は、「正二十面体群は5次の交代群と同型である。」という主張の証明の一部を行いました。
正二十面体を正十二面体群とみなして(同型だから)、頂点に着目して立方体を作り、立方体の頂点を回転させて頂点の対応を観察しました。

次回は、証明を完結させます。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。