本記事の内容
本記事は、固有値および固有ベクトルについて解説する記事です。
本記事を読むにあたり、行列、線型写像について知っている必要があるため、以下の記事も合わせてご覧ください。
↓行列の記事
↓線型写像の記事
固有値、固有ベクトルは線型代数の中で誠に重要な位置にいます。
「固有値、固有ベクトルって何スか?」という話の前に、固有値、固有ベクトルについてちょっと語ります。
とはいっても、実は固有値、固有ベクトルは誠にシンプルなコンセプトなのですが、シンプルであるにも関わらず、びっくりするくらい情報量が多い概念でもあります。
本ブログにおいては「対角化」および「三角化」をするために必要だ、という言い方にとどめておきますが、固有値、固有ベクトルはそれだけのためにあるのではありません。
グラフ理論の分野ではLaplacian(ラプラシアン)行列の固有値を専門的に調べる分野があるくらいには情報量が多いです。
グラフ理論ではLaplacian行列がグラフを表現するものであって、その行列から様々な特性を見出すことができます。
平たく言うと次がラプラシアン行列です。
- 頂点の次数、辺のある頂点というグラフの構造を行列で表現したもの。
- グラフの性質を行列の性質に置き換えて理解できる。
- 頂点に対する辺の入出力から、グラフにおける勾配と発散を表現したもの。
です。
この行列の固有値、固有ベクトルには、次の性質があります(めっちゃくちゃ平たく言います)。
グラフが非連結(つながってない部分があるようなグラフ)であるとき、ラプラシアン行列の成分は連結部分(つながっている部分)ごとにブロックで対角化できるため、「ここが一塊なんだな」など(適当かよ!)が分かります。
要するに、固有値、固有ベクトルは誠にシンプルなコンセプトである一方で誠に情報量が多いコンセプトでもあり、あらゆる分野で出現します。
先のグラフの例は幾何の分野になります。
ちなみに、筆者の専門(と言えるほど詳しくはないのですが)はグラフ理論で、幾何の中で一番好きな分野です。
点の繋がり方にのみ着目した幾何学で、初めて学んだときは「こんなにも面白い分野があるのか!よし。幾何を専門にしよう!」と意気込んでいたものです。
御託はいいから、さっさと固有値と固有ベクトルについて教えろ。
ですよね。
では、まず固有値と固有ベクトルがどういうコンセプトなのか、ということをイントロとして少々述べることにします。
まず、本記事では線型空間\(V\)か自分自身への線型写像を考察対象として、そのメカニズムを救命するために、基底をうま〜く選んで表現行列をより見やすいものにする、ということを考えます。
固有値、固有ベクトルはこのこの目的を達成するための1つのプロセスです。
固有値と固有ベクトル
つらつらと書いてきましたが、いよいよ数学の話に入ります。
まず、線型変換というものを定めます。
線型変換
簡単です。
というより先程もうすでに述べています。
線型空間\(V\)から自分自身\(V\)への線型写像を線型変換という。
単にこれだけです。
線型写像というと一般に2つの相異なる線型空間の間の写像というニュアンスがありますが、線型変換というと、1つの線型空間の中での話という限定的なものになります。
勿論、線型写像は2つの相異なる線型空間の写像のことだけを指すのではなくて、線型写像の中で、自身から自信への線型写像を線型変換と呼ぶ、という話になります。
従って、線型変換といったらば、「同じ線型空間から同じ線型空間への写像なんだな」と思ってください、ということです。
余談が過ぎるかもしれませんが、線型写像が満たすべき条件が2つありました。
線型写像
\(V\)および\(W\)を\(\mathbb{R}\)上の線型空間とする。\(V\)から\(W\)への写像\(f:V \to W\)が線型写像(a linear map)であるとは、次の1.および2.を満たすときを言う。- \(f(\boldsymbol{x}+\boldsymbol{y})=f(\boldsymbol{x})+f(\boldsymbol{y})\quad(\boldsymbol{x},\boldsymbol{y}\in X)\)
- \(f(\lambda\boldsymbol{x})=\lambda f(\boldsymbol{x})\quad(\lambda\in\mathbb{R},\boldsymbol{x}\in V)\)
この条件1.および2.において、左辺の\(+\)と右辺の\(+\)、左辺のスカラー倍と右辺のスカラー倍は厳密には違う演算だよ、という話をしました。
左辺の演算は\(V\)の中の演算、右辺の演算は\(W\)の中の演算だからです。
しかし、線型変換の場合は\(V\)から\(V\)への写像なので、左辺の演算と右辺の演算はまったくもって同じものです。
固有値、固有ベクトル
線型変換\(f: V\to V\)があたえられたとき、「あるベクトル\(\boldsymbol{v}\neq\boldsymbol{0}\)があって、\(f\)は\(\boldsymbol{v}\)を\(\boldsymbol{v}\)の定数倍に写すようにできるかな?」という素朴な疑問が出発点です。
式で書くと、
$$
f(\boldsymbol{v})=\lambda\boldsymbol{v}
$$
を満たすような\(\boldsymbol{v}\neq0\)が存在するか、ということになります。
ある種、中学校で習った比例のベクトルバージョンのようなものです。
この定数\(\lambda\)を固有値、ベクトル\(\boldsymbol{v}\)を固有値\(\lambda\)に対する固有ベクトルと言います。
しっかり書くと以下です。
固有値、固有ベクトル
線型変換\(f:V\to V\)に対して、 $$ f(\boldsymbol{v})=\lambda\boldsymbol{v},\quad \boldsymbol{v}\in V,\ \boldsymbol{v}\neq\boldsymbol{0},\ \lambda\in\mathbb{R} $$ を満たす\(\lambda\)を\(f\)の固有値(eigenvalue)、\(\boldsymbol{v}\)を固有値\(\lambda\)に属する固有ベクトル(eigenvector)という。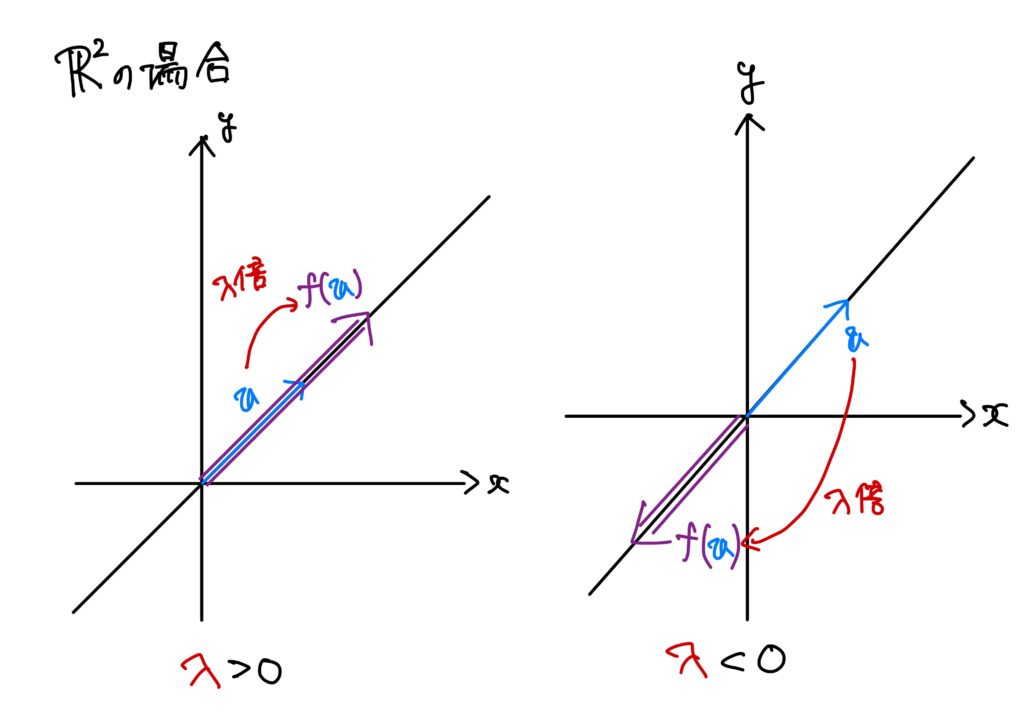
ね?シンプルでしょ?
こんなにシンプルなのに固有値、固有ベクトルは情報量が多いんですねえ。
「Simple is the best.」みたいな感じでしょうか(分かりませんが)。
ちなみに、なぜ\(\boldsymbol{v}\neq\boldsymbol{0}\)なのかというと、\(\boldsymbol{v}=\boldsymbol{0}\)とすると、\(f\)は線型写像なので\(\lambda\)が何であったとしても、常に
$$
f(\boldsymbol{v})=\lambda\boldsymbol{v}
$$
を満たしてしまい、意味をなさないためです。
ここで、今は\(\mathbb{R}\)上の線型空間について話していますが、複素数\(\mathbb{C}\)上の線型空間の線型変換についても\(\lambda\in\mathbb{C}\)として同様のコンセプトが定まります。
1つの固有値に対して固有ベクトルはいっぱいある。
そうなんです。いっぱいあるんです。
$$
f(\boldsymbol{v})=\lambda\boldsymbol{v}
$$
という式を見てみましょう。
仮に\(c(\neq0)\in\mathbb{R}\)と\(\boldsymbol{u}\in V\)を用いて、\(\boldsymbol{v}=c\boldsymbol{u}\)が成り立っているとします。
すると、
$$
f(\boldsymbol{v})=f(c\boldsymbol{u})
$$
であって、
$$
\lambda\boldsymbol{v}=\lambda c\boldsymbol{u}
$$
ですので、
$$
f(c\boldsymbol{u})=\lambda \left(c\boldsymbol{u}\right)
$$
となります。
従って、\(c\boldsymbol{u}\)も固有値\(\lambda\)の固有ベクトルです。
従って、固有ベクトルが1つ見つかれば、その定数倍はすべて固有ベクトルとなるわけですので、固有ベクトルはいっぱいある、ということになります。
固有空間
固有空間というものを定めるために以下の定理を証明します。
定理1.
線型空間\(V\)の線型変換\(f\)の固有値の1つを\(\lambda\)とする。\(\lambda\)に属する\(f\)の固有ベクトル全体と零ベクトルからなる集合\(V(\lambda)\)は集合 $$ \left\{\boldsymbol{v}\in V\middle|f(\boldsymbol{v})=\lambda\boldsymbol{v}\right\} $$ と一致して、\(V\)の部分空間である。定理1.の証明
簡単です。
なんてことありません。
\(V(\lambda)\)を明示すると、
$$
V(\lambda)=\left\{\boldsymbol{v}\in V\middle| \boldsymbol{v}\neq\boldsymbol{0},\ f(\boldsymbol{v})=\lambda\boldsymbol{v} \right\}\cup \{\boldsymbol{0}\}
$$
です。
ここで、先に述べたように、\(f(\boldsymbol{0})=\boldsymbol{0}=\lambda\boldsymbol{0}\)により、\(\boldsymbol{0}\)も\(f(\boldsymbol{v})=\lambda\boldsymbol{v}\)を満たします。
従って、
$$
V(\lambda)=\left\{\boldsymbol{v}\in V\middle| f(\boldsymbol{v})=\lambda\boldsymbol{v} \right\}
$$
です。
次に\(V(\lambda)\)が\(V\)の部分空間であることを示します。
次の事実を使います。
定理2.(部分空間の必要十分条件)
線型空間\(V\)の部分集合\(W\)が部分空間であるための必要十分条件は次の3条件が成り立つことである。- \(W\neq \emptyset\quad\)(\(\emptyset\)は空集合)
- \(\boldsymbol{a},\boldsymbol{b}\in W\Rightarrow \boldsymbol{a}+\boldsymbol{b}\in W\)
- \(\boldsymbol{a}\in W\)、\(\lambda\in\mathbb{R}\Rightarrow\lambda\boldsymbol{a}\in W\)
先に調べたように、\(\boldsymbol{0}\in V(\lambda)\)ですので、\(V(\lambda)\neq\emptyset\)です。
\(\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}\in V\)、\(k\in\mathbb{R}\)に対して、
\begin{eqnarray}
&&f(\boldsymbol{v}_1+\boldsymbol{v}_2)=f(\boldsymbol{v}_1+\boldsymbol{v}_2)=\lambda\boldsymbol{v}_1+\lambda\boldsymbol{v}_2=\lambda(\boldsymbol{v}_1+\boldsymbol{v}_2)\\
&&
f(k\boldsymbol{v})=kf(\boldsymbol{v})=k\lambda\boldsymbol{v}=\lambda\left( k\boldsymbol{v}\right)
\end{eqnarray}
であるので、
$$
\boldsymbol{v}_1+\boldsymbol{v}_2\in V(\lambda),\quad k\boldsymbol{v}\in V(\lambda)
$$
となるから、\(V(\lambda)\)は\(V\)の部分空間になります。
定理1.の証明終わり
この\(V(\lambda)\)を\(f\)の固有値\(\lambda\)に属する固有空間と言います。
ここで、線型写像は行列で表現され、逆に行列は線型写像で表現できるということを思い出しておきます(※これについては【線型代数学の基礎シリーズ】行列編 その5を御覧ください)。
すると、今までの線型変換の話を行列の話に置き換えることができます。
行列の固有値、固有ベクトル、固有空間
\(n\in\mathbb{N}\)とするとき、\(n\)次正方行列\(A\)は、対応\(\boldsymbol{x}\mapsto A\boldsymbol{x}\)により\(\mathbb{R}^n\)の線型変換\(f_A:\mathbb{R}^n\to\mathbb{R}^n\)を定める。\(f_A\)の固有値、固有ベクトル、固有空間をそれぞれ\(A\)の固有値、固有ベクトル、固有空間という。すなわち、\(f_A\)の固有空間とは、\(\lambda\)を\(f_A\)の固有値としたとき $$ V(\lambda)=\left\{\boldsymbol{v}\in V\middle| f_A(\boldsymbol{v})=\lambda\boldsymbol{v} \right\} $$ を指す。「固有値、固有ベクトルって必ず存在すんのけ?」「いいえ、存在しないときもあります。」
さも必ず存在するかのように書いてきましたが、実は存在しない場合もあります。
例えば次のような場合です。
例3.\(\displaystyle A=\begin{pmatrix}0&1 \\-1&0\\ \end{pmatrix}\)で与えられる線型変換\(A:\mathbb{R}^2\to\mathbb{R}^2\)を考えます。
このとき、
$$
A\boldsymbol{x}=\lambda\boldsymbol{x},\quad \boldsymbol{x}=\left(\begin{array}{c}x\\ \\ y \end{array}\right)
$$
を満たすような\(\lambda\in\mathbb{R}\)と\(\boldsymbol{x}\neq\boldsymbol{0}\)が存在したとすると、
$$
\begin{pmatrix}0&1 \\-1&0\\ \end{pmatrix}\left(\begin{array}{c}x\\ \\ y \end{array}\right)=\lambda\left(\begin{array}{c}x\\ \\ y \end{array}\right)
$$
により、
$$
\begin{cases}y=\lambda x\\
-x=\lambda y\end{cases}
$$
となって、\(-x=\lambda(\lambda x)=\lambda^2x\)となるから\((\lambda^2+1)x=0\)となって、\(x=0\)で、\(y=0\)です。
すなわち\(\boldsymbol{x}=\boldsymbol{0}\)です。
固有ベクトルは零ベクトルではないので、これは固有ベクトルではありません。
従って、この行列には固有値も固有ベクトルも存在しません。
連立斉一次方程式の解の存在
なんでいきなり連立一次方程式の解の存在について述べるんだ?と思うかもしれまん。
確かに、連立一次方程式の部分で述べれば良いようなものですが、そこで述べたとしても「なんでこんなことすんの?」というのが見えなくなりそうだな、と思ったので、必要なところが出てきたらば述べる、ということにしました。
連立斉一次方程式の解の存在は後述する固有値を求める際に使います。
連立斉一次方程式
連立斉一次方程式とは以下の連立方程式を指します。
$$
\begin{cases}
a_{11}x_1+\dots+a_{1n}x_n=0&(1)\\
a_{21}x_1+\dots+a_{2n}x_n=0&(2)\\
\qquad \vdots\qquad \vdots\\
a_{n1}x_1+\dots+a_{nn}x_n=0&(n)\\
\end{cases}
$$
すなわち、この方程式の係数行列を\(A\)としたとき、\(A\boldsymbol{x}=\boldsymbol{0}\)の形の方程式を連立斉一次方程式と言います。
この方程式は\(\boldsymbol{x}=\boldsymbol{0}\)を必ず解に持ち(代入すると分かります)、これを自明な解といいます。
この方程式の解の存在について次が成り立ちます。
連立斉一次方程式の自明な解以外の解を持つための必要十分条件
定理4.
連立斉一次方程式\(A\boldsymbol{x}=\boldsymbol{0}\)が自明な解以外の解を持つための必要十分条件は\(\det(A)=0\)である。定理4.の証明
(1.「自明な解以外の解を持つ\(\Rightarrow\det(A)=0\)」の証明)
もし仮に\(\det(A)\neq0\)だったとします(背理法)。
このとき、\(A\)の逆行列\(A^{-1}\)が存在するため、連立斉一次方程式\(A\boldsymbol{x}=\boldsymbol{0}\)の解\(\boldsymbol{x}\)は
$$
\boldsymbol{x}=A^{-1}\boldsymbol{0}=\boldsymbol{0}
$$
となり、かつ一意的です。
従って、\(\boldsymbol{x}=\boldsymbol{0}\)以外の解を持ちません。
これは矛盾です。
故に\(\det(A)=0\)です。
(2.「\(\det(A)=0\Rightarrow\)自明な解以外の解を持つ」の証明)
\(n\in\mathbb{N}\)に関する数学的帰納法で証明します。
\(\det(A)=0\)とします。
\(n=1\)の場合は\(\det(A)=a_{11}=0\)なので、\(A\boldsymbol{x}=\boldsymbol{0}\)は\(a_{11}x_11=0\)でかつ\(a_{11}=0\)なのだから、\(x_1\)はどんな数でも良いです。
従って、任意の数が解となります。
\(n>1\)としましょう。
第1列の\(a_{i1}\ (i=1,\dots,n)\)がすべて\(0\)であれば、任意の数\(x_1\)に対して
$$
\boldsymbol{x}=
\left(
\begin{array}{c}
x_1\\
0\\
\vdots \\
0
\end{array}
\right)
$$
が解になります。次にある成分\(a_{i1}\)が\(0\)出ないとすると、式の並び替える順序を変えて\(a_{11}\neq0\)とできるため、\(a_{11}\neq0\)とします。
方程式\(A\boldsymbol{x}=\boldsymbol{0}\)(これを①式と名付けます)を変形して、
$$
②\begin{cases}
a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=0&(1)\\
a_{22}^\prime x_2+\dots+a_{2n}^\prime x_n=0&\displaystyle(2)^\prime=(2)-(1)\times\frac{a_{21}}{a_{11}}\\
\qquad \vdots\qquad \vdots\\
a_{n2}^\prime x_2+\dots+a_{nn}^\prime x_n=0&\displaystyle(n)^\prime=(n)-(1)\times\frac{a_{n1}}{a_{11}}\\
\end{cases}
$$
とします。
逆に②の式から同様に①式が導かれますので、①と②の方程式の解は一致します。
また、方程式②の係数行列を\(A^\prime\)とし、以下の事実を使います。
定理5.
行列の1つの行に任意の数を掛けて、他の行に加えても、行列式の値は変わらない。すなわち、\(n\in\mathbb{N}\)、\(A=\left( A_{ij}\right)\)を\(n\)次正方行列とする。このとき、 $$ \begin{array}{c} \\ \\ i行\rightarrow\\ \\ j行\rightarrow\\ \\ \\ \end{array} \left| \begin{array}{c} a_{11}&\cdots &a_{1n}\\ \vdots&&\vdots\\ a_{i1}+ca_{j1}&\cdots&a_{in}+ca_{jn}\\ \vdots&&\vdots\\ a_{j1}&\cdots&a_{jn}\\ \vdots&&\vdots\\ a_{n1}&\cdots&a_{nn}\\ \end{array}\right| = \left| \begin{array}{c} a_{11}&\cdots &a_{1n}\\ \vdots&&\vdots\\ a_{i1}&\cdots&a_{in}\\ \vdots&&\vdots\\ a_{j1}&\cdots&a_{jn}\\ \vdots&&\vdots\\ a_{n1}&\cdots&a_{nn}\\ \end{array}\right| \begin{array}{c} \\ \\ \leftarrow i行\\ \\ \leftarrow j行 \\ \\ \end{array} $$ が成り立つ。定理5.の証明は【線型代数学の基礎シリーズ】行列式編 その3を御覧ください。
すなわち、\(A^\prime\)は\(A\)に対して行基本変形を行った行列ですので、行列式の値は変わりません。
今、\(\det(A)=0\)なのですから、\(\det(A)=\det(A^\prime)=0\)が成り立ちます。
そして、更に次の事実を使います。
定理6.
$$ \left| \begin{array}{c} a_{11}&a_{12}&\cdots &a_{1n}\\ 0&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ 0&a_{n2}&\cdots &a_{nn}\\ \end{array}\right|=a_{11} \left| \begin{array}{c} a_{22}&\cdots &a_{2n}\\ \vdots& \ddots&\vdots\\ a_{n2}&\cdots &a_{nn}\\ \end{array}\right| $$定理6.の証明は【線型代数学の基礎シリーズ】行列式編 その2を御覧ください。
定理6.を使うと、
$$
0=\det(A^\prime)=
\left|
\begin{array}{c}
a_{11}&a_{12}&\cdots &a_{1n}\\
0&a_{22}^\prime&\cdots &a_{2n}^\prime\\
\vdots&\vdots& \ddots&\vdots\\
0&a_{n2}^\prime&\cdots &a_{nn}^\prime\\
\end{array}\right|=a_{11}
\left|
\begin{array}{c}
a_{22}^\prime&\cdots &a_{2n}^\prime\\
\vdots& \ddots&\vdots\\
a_{n2}^\prime&\cdots &a_{nn}^\prime\\
\end{array}\right|
$$
です。
今、\(a_{11}\neq0\)だったわけですので、
$$
\left|
\begin{array}{c}
a_{22}^\prime&\cdots &a_{2n}^\prime\\
\vdots& \ddots&\vdots\\
a_{n2}^\prime&\cdots &a_{nn}^\prime\\
\end{array}\right|=0
$$
です。
そこで、\(n-1\)個の未知数\(x_2,x_3,\dots,x_n\)に関する連立斉一次方程式
$$
③\begin{cases}
a_{22}^\prime x_2+\dots+a_{2n}^\prime x_n=0\\
\qquad \vdots\qquad \vdots\\
a_{n2}^\prime x_2+\dots+a_{nn}^\prime x_n=0\\
\end{cases}
$$
を考えると、今の話から係数行列は\(A^\prime\)であって、\(\det(A^\prime)=0\)なのだから、帰納法の仮定から自明でない解を持つことになります(今、\(n-1\)まで成り立ったとして、\(n\)のときはどうか、という話をしていたので、\(n-1\)のときは成り立っているという仮定を置いています)。
その自明でない解のうちの1つを\((d_2,\dots.d_n)\)としましょう。
これを①に代入して、方程式
$$
a_{11}x_1+a_{12}d_2+\dots+a_{1n}d_n=0
$$
を得ます。
\(a_{11}\neq0\)なのですから、\(x_1\)に関するこの方程式は解を持ち、その解を\(d_1\)とすれば、
$$
x_1=d_1=-\frac{a_{12}}{a_11}d_2-\dots-\frac{a_{1n}}{a_11}d_n
$$
このようにして得られた\((d_1,d_2,\dots,d_n)\)は②の解です。
従って、①の解です。
しかも、\((d_2,\dots.d_n)\)は自明でない解なのですから、この解\((d_1,d_2,\dots,d_n)\)も自明でない解です。
定理4.の証明終わり
やっぱり行列式が持つ情報量は多いですねえ。
固有多項式と固有方程式
では、固有値、固有ベクトルの話に戻ります。
固有値と固有ベクトルが存在するような線型変換の例
先程、「固有値と固有ベクトルは必ずしも存在しない」ということを例3.で示しました。
今回は、固有値と固有ベクトルが存在するような線型変換の例を挙げます。
例7.\(\displaystyle A=\begin{pmatrix}4&3 \\1&2\\ \end{pmatrix}\)で与えられる線型変換\(A:\mathbb{R}^2\to\mathbb{R}^2\)を考えます。
今、\(A\)の固有値\(\lambda\)と\(\lambda\)に属する固有ベクトル
$$
\boldsymbol{x}=
\left(
\begin{array}{c}
x\\
y\\
\end{array}\right)\neq\boldsymbol{0}
$$
が存在したとしましょう。
このとき、
\begin{eqnarray}
&&\begin{pmatrix}
4&3\\
1&2\\
\end{pmatrix}
\left(
\begin{array}{c}
x\\
y\\
\end{array}\right)
=\lambda
\left(
\begin{array}{c}
x\\
y\\
\end{array}\right)\\
&\Leftrightarrow&
\begin{cases}
4x+3y=\lambda x\\
x+2y=\lambda x
\end{cases}\\
&\Leftrightarrow&
\begin{cases}
(4-\lambda)x+3y=0\\
x+(2-\lambda)y=0
\end{cases}
\end{eqnarray}
です。
先程示したように定理4.からこの連立一次方程式が\(\boldsymbol{0}\)でない解(自明でない解)を持つための必要十分条件は
$$
\left|
\begin{array}{c}
4-\lambda&3\\
1&2-\lambda\\
\end{array}
\right|=0
$$
です。
これをより端的に書くと
$$
\left|A-\lambda I_2\right|=\det\left( A-\lambda I_2\right)=0
$$
となることに注意してください。
ここで、\(\lambda\)という記号を\(t\)に置き換えた左辺の行列式を\(\varphi_A(t)\)とします。
すなわち、
\begin{eqnarray}
\varphi_A(t)&=&\left|
\begin{array}{c}
4-t&3\\
1&2-t\\
\end{array}
\right|\\
&=&(t-4)(t-2)-3\\
&=&t^2-6t+8-3\\
&=&(t-1)(t-5)
\end{eqnarray}
です。
このとき、\(\lambda\)が行列\(A\)の固有値であることと、\(\lambda\)が\(\varphi_A(t)=0\)の解となることは同値です。
従って、\(1\)と\(5\)がこの行列\(A\)の固有値だと分かります。
また、固有ベクトルについては
$$
\begin{cases}
(4-\lambda)x+3y=0\\
x+(2-\lambda)y=0
\end{cases}
$$
の自明でない解で、今
$$
\left|
\begin{array}{c}
4-\lambda&3\\
1&2-\lambda\\
\end{array}
\right|=0
$$
なのですから、これも定理4.から\(\lambda=1,5\)に属する固有ベクトルの存在が保証されています。
\(\lambda\)が行列\(A\)の固有値であることの必要十分条件
先程の考察はそのまんま、一般の線型変換に対しても成り立ちます。
つまり、以下が成り立ちます。
定理8.(\(\lambda\)が行列\(A\)の固有値であるための必要十分条件)
\(n\in\mathbb{N}\)とし、\(A\)を\(n\)次正方行列とする。このとき\(\lambda\)が\(A\)の固有値であるための必要十分条件は $$ \det\left( A-\lambda I_n\right)=0 $$ である。ただし、\(I_n\)は\(n\)次の単位行列である。定理8.の証明
さっきと同じことをします。
\(\lambda\in\mathbb{R}\)が\(A\)の固有値であるとは、\(A\boldsymbol{x}=\lambda\boldsymbol{x}\)となる\(\boldsymbol{0}\)でないベクトル\(\boldsymbol{x}\)が存在することです。
ここで、\(n\)次の単位行列\(I_n\)をいると\(\lambda\boldsymbol{x}\)は
$$
\lambda\boldsymbol{x}=\lambda I_n\boldsymbol{x}
$$
と書かれます。
行列\(A\)と行列\(\lambda I_n\)はともに\(n\)次の正方行列ですので、行列の積を考えることができます。
ここで、行列の積に関する分配法則を使います。
具体的には以下の2.です。
定理9.(分配則)
\(m,n,r\in\mathbb{N}\)、\(k,h\in\mathbb{C}\)とする。このとき、3つの行列\(C\)に対して、以下が成り立つ。- \(A\)が\((m,n)\)型、\(B\)及び\(C\)が\((n,r)\)型のとき、\(A(B+C)=AB+AC\)
- \(A\)と\(B\)が\((m,n)\)型、\(C\)が\((n,r)\)型のとき、\((A+B)C=AC+BC\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\(k(A+B)=kA+kB\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\((k+h)A=kA+hA\)
定理9.の証明は【線型代数学の基礎シリーズ】行列編 その2を御覧ください。
定理9.の2.を使うと、
$$
A\boldsymbol{x}-\lambda\boldsymbol{x}=A\boldsymbol{x}-\lambda I_n\boldsymbol{x}=\left( A-\lambda I_n\right)\boldsymbol{x}
$$
となります。
従って、\(\lambda\)が\(A\)の固有値となることと、連立斉一次方程式
$$
\left( A-\lambda I_n\right)\boldsymbol{x}=\boldsymbol{0}
$$
が自明でない解\(\boldsymbol{x}\neq\boldsymbol{0}\)を持つことは同値です。
またまた定理4.からこのことは
$$
\det\left( A-\lambda I_n\right)=0
$$
となることは同値です。
定理8.の証明終わり
「あれ?固有多項式と固有方程式の話じゃなかったッスか?」「そうです。今話します。」
固有多項式と固有方程式を忘れていたわけではありませんよ。
ちゃんと話します。
とはいえ、この章でのべた\(\varphi_A(t)\)を固有多項式と呼び、\(\varphi_A(t)=0\)を固有方程式と呼ぶ、という単にそれだけです。
以下に明示します。
固有多項式、固有方程式
\(n\)次正方行列\(A=\left( a_{ij}\right)\)に対して、 $$ \varphi_A(t)=\det\left( A-tI_n\right) = \left| \begin{array}{c} a_{11}-t&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}-t&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{n1}&a_{n2}&\cdots &a_{nn}-t\\ \end{array}\right| $$ によって定められる変数\(t\)についての多項式\(\varphi_A(t)\)を行列\(A\)の固有多項式まはた特性多項式といい、 $$ \varphi_A(t)=0 $$ を行列\(A\)の固有方程式という。固有方程式の言葉を使うことで、定理8.は次のように言い換えることができます。
定理8′.(\(\lambda\)が行列\(A\)の固有値であるための必要十分条件)
\(n\in\mathbb{N}\)とし、\(A\)を\(n\)次正方行列とする。このとき\(\lambda\)が\(A\)の固有値であるための必要十分条件は、\(\lambda\)が\(A\)の固有方程式 $$ \varphi_A(t)=0 $$ の解になることである。ただし、\(I_n\)は\(n\)次の単位行列である。いっちょ固有値と固有空間を計算してみっか。
してみましょう。
例10.\(\displaystyle
A=
\begin{pmatrix}
7&-2\\
4&1\\
\end{pmatrix}\)で与えられる線型変換\(A:\mathbb{R}^2\to\mathbb{R}^2\)を考えます。
この\(A\)について、\(A\)の固有多項式\(\varphi_A(t)\)、\(A\)の固有値\(\lambda\)、\(A\)の各固有値\(\lambda\)に属する固有空間\(V(\lambda)\)を求めてみます。
\(A\)の固有多項式\(\varphi_A(t)\)は
$$
\varphi_A(t)=\det(A-tI_2)=
\left|
\begin{array}{c}
7&-2\\
4&1\\
\end{array}\right|=t^2-8t+15
$$
です。
従って、\(A\)の固有値は\(\lambda=3,5\)です。
固有空間\(V(3)\)および\(V(5)\次のように求めます。
- \(\lambda=3\)のとき
$$
\left(A-3\lambda I_2\right)\boldsymbol{x}=
\begin{pmatrix}
7-3&-2\\
4&1-3\\
\end{pmatrix}
\left(
\begin{array}{c}
x\\
y\\
\end{array}\right)
=\begin{pmatrix}
4&-2\\
4&-2\\
\end{pmatrix}
\left(
\begin{array}{c}
x\\
y\\
\end{array}\right)
$$
の解は
$$
\boldsymbol{x}=c\left(
\begin{array}{c}
1\\
2\\
\end{array}\right)\quad(c\in\mathbb{R})
$$
です。
実際、\(4x-2y=0\)により\(y=2x\)なので、\(x=1\)のとき\(y=2\)で、その定数倍がすべて\(y=2x\)を満たしているからです。
これは最初の方に述べた、「固有ベクトルはいっぱいあって、固有ベクトルの定数倍もまた固有ベクトルである」ということです。
勿論、固有ベクトルを\(x=123\)、\(y=246\)として
$$
\boldsymbol{x}=c\left(\begin{array}{c}123\\246\\ \end{array}\right)\quad(c\in\mathbb{R})
$$
としてもOKですが、このような表現はほぼ使いません。なるべく整数の形で書くのが一般的です。
従って、\(\lambda=3\)のときの固有空間\(V(3)\)は
$$
V(3)=\left\{c\left(\begin{array}{c}1\\2\\ \end{array}\right)\middle|c\in\mathbb{R}\right\}
$$
です。 - \(\lambda=5\)のとき
$$\left(A-3\lambda I_2\right)\boldsymbol{x}=\begin{pmatrix}
7-5&-2\\
4&1-5\\
\end{pmatrix}
\left(
\begin{array}{c}
x\\
y\\
\end{array}\right)
=\begin{pmatrix}
2&-2\\
4&-4\\
\end{pmatrix}
\left(
\begin{array}{c}
x\\
y\\
\end{array}\right)
$$
の解は
$$
\boldsymbol{x}=c\left(
\begin{array}{c}
1\\1\\
\end{array}\right)\quad(c\in\mathbb{R})
$$
です。
実際、\(2x-2y=0\)により\(y=x\)なので、\(x=1\)のとき\(y=x\)で、その定数倍がすべて\(y=x\)を満たしているからです。
従って、\(\lambda=5\)のときの固有空間\(V(5)\)は
$$
V(5)=\left\{c\left(\begin{array}{c}1\\1\\ \end{array}\right)\middle|c\in\mathbb{R}\right\}
$$
です。
なぜ今まで行列式やら何やらの性質を学んでいたかというと、固有値を求めるため、ということが①つの目標だったからです。
余談(\(C\)上の線型空間における固有値)
固有方程式の解は例3.でみたように、必ずしも存在するわけではありません。もし考えている線型空間が\(\mathbb{C}\)上の線型空間であれば、固有値も\(\mathbb{C}\)の範囲で考えます。
従って、固有方程式もその解も\(\mathbb{C}\)の範囲で考えます。
そして、代数学の基本定理としてよく知られているように、一般に\(n\)次の方程式は複素数の範囲で、重複を含めてちょうど\(n\)個の解を持っています。
それを\(\lambda_1,\dots,\lambda_n\)とおくと、固有多項式\(\varphi_A(t)\)は次のように因数分解されます。 $$ \varphi_A(t)=(-1)^n(t-\lambda_1)\dots(t-\lambda_n) $$ 故に、\(\mathbb{C}\)上の線型空間に置いては必ず固有値を持ちます。
これが\(\mathbb{R}\)上の線型空間と\(\mathbb{C}\)上の線型空間との本質的な違いでもあります。
線型写像の固有値
線型写像は行列で表現され、逆に行列は線型写像で表現できるのでした。
従って、線型変換も行列で表現され、正方行列は線型変換で表現できます。
故に次が成り立ちます。
定理11.
線型変換\(f:V\to V\)が与えられたとき、\(V\)の1つの基底をとり、その基底に関する\(f\)の表現行列を\(A\)とする。このとき、\(f\)の固有値の集合は招福を込めて\(A\)の固有値の集合と一致する。線型写像と行列の関係を知っていると「そりゃそうじゃね?」という話ですが、証明します。
とはいえ、一瞬です。
定理11.の証明
\(\boldsymbol{v}_1,\dots,\boldsymbol{v}_n\)を\(V\)の1組の基底とします。
\(V\)のベクトル\(\boldsymbol{x}\)をこの基底の線型結合
$$
\boldsymbol{x}=x_1\boldsymbol{v}_1+\dots+x_n\boldsymbol{v}_n
$$
で書いたとします。
そのとき、
$$
f(\boldsymbol{x})=\lambda\boldsymbol{x}
$$
と
$$
A
\left(\begin{array}{c}x_1\\ \vdots \\ x_n\end{array}\right)=\lambda\left(\begin{array}{c}x_1\\ \vdots \\ x_n\end{array}\right)
$$
とは同値であるため、主張が成り立ちます。
定理11.の証明終わり
特別な行列の固有値
特別な形の行列は固有多項式を計算するまでもなくスッと求まることがあります。
勿論これは行列式の性質が故です。
三角行列の固有値
これはめちゃくちゃ計算しやすいです。
すでに我々は行列式の諸性質について学んでいるので、わざわざ書かずともよいかもしれませんが、知っていると余計な計算をせずに済みますので、書きます。
三角行列は何だったかというと、以下でした。
三角行列
- 上三角行列 対角線より左下の成分がすべて\(0\)であるような行列 $$ \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ 0&a_{22}&\cdots &a_{2n}\\ \vdots&\ddots& \ddots&\vdots\\ 0&\cdots&0 &a_{nn}\\ \end{pmatrix} $$ を上三角行列という。
- 下三角行列 対角線より右上の成分がすべて\(0\)であるような行列 $$ \begin{pmatrix} a_{11}&0&\cdots &0\\ a_{21}&a_{22}&\ddots &\vdots\\ \vdots&\vdots& \ddots&0\\ a_{n1}&a_{n2}&\cdots &a_{nn}\\ \end{pmatrix} $$ を下三角行列という。
\(A\)を\(n\)次の三角行列だとします。
すなわち、
$$
A=\begin{pmatrix}
a_{11}&a_{12}&\cdots &a_{1n}\\
0&a_{22}&\cdots &a_{2n}\\
\vdots&\ddots& \ddots&\vdots\\
0&\cdots&0 &a_{nn}\\
\end{pmatrix}\quad \mbox{または}\quad
\begin{pmatrix}
a_{11}&a_{12}&\cdots &a_{1n}\\
0&a_{22}&\cdots &a_{2n}\\
\vdots&\ddots& \ddots&\vdots\\
0&\cdots&0 &a_{nn}\\
\end{pmatrix}
$$
とします。
この行列\(A\)の固有多項式を考えてみます。
行列\(A-t I_n\)は
$$
A-tI_n=\begin{pmatrix}
a_{11}-t&a_{12}&\cdots &a_{1n}\\
0&a_{22}-t&\cdots &a_{2n}\\
\vdots&\ddots& \ddots&\vdots\\
0&\cdots&0 &a_{nn}-t\\
\end{pmatrix}\quad \mbox{または}\quad
\begin{pmatrix}
a_{11}-t&a_{12}&\cdots &a_{1n}\\
0&a_{22}-t&\cdots &a_{2n}\\
\vdots&\ddots& \ddots&\vdots\\
0&\cdots&0 &a_{nn}-t\\
\end{pmatrix}
$$
となるので、やはり三角行列です。
従って固有多項式は\(\varphi_A(t)=\det(A-tI_n)\)はどちらの場合も対角成分の積で表すことができます。
実際、次の事実が成り立っていたからです。
命題12.
\(n\)次上三角行列\(A\)の行列式\(\det(A)\)は\(A\)の対角成分の積に等しい。すなわち、次が成り立つ。 $$ \det(A)=a_{11}a_{22}\dots a_{nn} $$命題12.の証明は【線型代数学の基礎シリーズ】行列式編 その2を御覧ください。
従って、\(\varphi_A(t)=\det(A-tI_n)\)は
$$
\varphi_A(t)=\det(A-tI_n)=(a_{11}-t)(a_{22}-t)\cdots(a_{nn}-t)
$$
となって、固有値は固有方程式\(\varphi_A(t)=0\)の解なので、
$$
\varphi_A(t)=\det(A-tI_n)=(a_{11}-t)(a_{22}-t)\cdots(a_{nn}-t)=0
$$
の解だから、\(A\)の固有値\(\lambda\)は
$$
\lambda=a_{11},a_{22},\dots,a_{nn}
$$
となり、対角成分そのものが固有値となります。
まとめると、次の主張になります。
定理13.
\(n\)次正方行列\(A\)が三角行列である時、\(A\)の固有値全体は重複も込めて\(A\)の対角成分と一致する。とどのつまり、
ということです。
ブロックに分かれている行列の固有値
ブロックに分かれている行列も計算しやすいです。
定理14.
\(n\)次正方行列\(A\)が $$ A=\begin{pmatrix} B&C\\ O&D\\ \end{pmatrix} $$ の形をしているとする。ここで\(B\)は\(r\)次正方行列、\(C\)は\((r,s)\)型の行列、\(D\)は\(s\)次正方行列、\(O\)は\((s,r)\)型の零行列とする。このとき、 $$ \varphi_A(t)=\varphi_B(t)\cdot\varphi_D(t) $$ が成り立つ。従って、行列\(A\)の固有値の全体は、重複も込めて行列\(B\)の固有値と行列\(D\)の固有値をあわせたものと一致する。定理14.の証明
なんてことありません。
\(n\)次の単位行列を\(I_n\)と書いたとすると、
$$
I_n=\begin{pmatrix}
I_r&O_{rs}\\
O_{sr}&I_s\\
\end{pmatrix}
$$
と書くことができます。
ただし、\(O_{rs}\)は\((r,s)\)型の零行列、\(O_{sr}\)は\((s,r)\)型の零行列です。
このとき、
$$
\varphi_A-tI_n=
\begin{pmatrix}
B&C\\
O&D\\
\end{pmatrix}-t\begin{pmatrix}
I_r&O_{rs}\\
O_{sr}&I_s\\
\end{pmatrix}=
\begin{pmatrix}
B-tI_r&C\\
O&D-tI_s\\
\end{pmatrix}
$$
です。
ここで、以下の事実を使います。
定理15.
\(X\)を\(n\)次正方行列とし、\(n=r+s\)を満たすような自然数\(r,s\)に対して、\(A\)を\(r\)次正方行列、\(B\)を\((r,s)\)型の行列、\(O\)を\((s,r)\)型の零行列、\(D\)を\(s\)次正方行列とする。このとき、 $$ |X|= \left| \begin{array}{c} A&B\\ O&D\\ \end{array} \right|=|A|\cdot|D| $$ である。定理15.の証明は【線型代数学の基礎シリーズ】行列式編 その2を御覧ください。
定理15.から、\(\varphi_A-tI_n\)の行列式\(\left|\varphi_A-tI_n\right|\)は
$$
\left|\varphi_A-tI_n\right|=
\left|\begin{array}{c}
B-tI_r&C\\
O&D-tI_s\\
\end{array}\right|=\left|B-tI_r \right|\cdot\left|D-tI_s\right|=\varphi_B(t)\cdot \varphi_D(t)
$$
となります。
従って、\(A\)の固有値は\(\varphi_B(t)\cdot \varphi_D(t)=0\)の解なので\(B\)と\(D\)の固有値をあわせたものと一致します。
定理14.の証明終わり
相似な行列
これは次回の対角化とも関わってきますので、少々先取りとして話します。
中学校のとき、三角形の合同と相似を学習したかと思います。
三角形の相似は要するに「2つの三角形のうち、一方の三角形を拡大、または縮小することでもう一方と一致する」ということでした。
とどのつまり形が同じで大きさが違うという”似ている”図形でした。
これは図形に対する相似でしたが、数学ではもっと別のものにも相似という概念があります。
実は行列にもあります。
つまり、”似た行列”というのが相似が行列です。
相似な行列
\(n\)次正方行列\(A\)および\(B\)に対して、 $$ B=P^{-1}AP $$ となる正則行列\(P\)が存在するとき、\(A\)と\(B\)は相似であるという。「どこが似てるんだよ」と思うかもしれませんが、実は、相似な行列同士は固有値が一致します。
そういう意味で”似ている”という事ができます(勿論他にも性質はありますが)。
定理16.
\(n\)次正方行列\(A\)および\(B\)が相似であれば、 $$ \varphi_A(t)=\varphi_B(t) $$ である。従って、\(A\)と\(B\)の固有値全体は重複を込めて一致する。定理16.の証明
簡単です。
なんてことありません。
まず、\(\varphi_B(t)=\left|B-tI_n\right|=\left|P^{-1}AP-tI_n \right|\)です。
単位行列\(I_n\)は行列の積においてどの順序でかけても変わらないので、
\begin{eqnarray}
\varphi_B(t)&=&\left|P^{-1}AP-tI_n \right|\\
&=&\left|P^{-1}AP-P^{-1}tI_nP \right|\\
&=&\left|P^{-1}(A-tI_n)P \right|\\
\end{eqnarray}
です。
ここで、次の事実を使います。
定理17.
\(n\in\mathbb{N}\)、\(A\)および\(B\)が共に\(n\)次正方行列とする。 このとき、次が成り立つ。 $$ \det(AB)=\det(A)\det(B) $$定理17.の証明は【線型代数学の基礎シリーズ】行列式編 その6を御覧ください。
定理17.を使って、
\begin{eqnarray}
\varphi_B(t)&=&\left|P^{-1}(A-tI_n)P \right|\\
&=&\left|P^{-1}\right|\cdot\left| A-tI_n\right|\cdot\left|P \right|
\end{eqnarray}
です。
また、次の事実を使います。
定理18.
正則行列\(A\)に対して、以下が成り立つ。 $$ \det(A^{-1})=\det(A)^{-1} $$定理18.の証明は【線型代数学の基礎シリーズ】行列式編 その6を御覧ください。
定理18. を用いると、
\begin{eqnarray}
\varphi_B(t)&=&\left|P^{-1}\right|\cdot\left| A-tI_n\right|\cdot\left|P \right|\\
&=&\left| P\right|^{-1}\cdot \left| A-tI_n\right|\cdot\left| P\right|
\end{eqnarray}
ここで、行列式は実数ですので、上記の式は実数の掛け算ですから、
\begin{eqnarray}
\varphi_B(t)&=&\left| P\right|^{-1}\cdot \left| A-tI_n\right|\cdot\left| P\right|\\
&=&\left| P\right|^{-1}\cdot \left| P\right|\cdot\left| A-tI_n\right|\\
&=&1\cdot\left| A-tI_n\right|\\
&=&\left| A-tI_n\right|=\varphi_A(t)
\end{eqnarray}
となります。
定理16.の証明終わり
小咄
線型変換\(f:V\to V\)が与えられたとき、\(V\)の1つの基底をとり、その規定に関して\(f\)を行列表示した行列を\(A\)としましょう。
そのとき、行列\(A\)の固有多項式\(\varphi_A(t)\)は基底のとり方に依存しません。
というのも、基底のとりかえは先の相似の関係になるからです。
つまり、基底のとりかえとは\(A\)に正則行列\(P\)を使って\(B=P^{-1}AP\)という操作をすることで得られて、この\(B\)が基底を取り替えた後の\(f\)の行列表示となっているというわけです。
従って、固有多項式というのは行列に対してのコンセプトではなく、より広く線型変換に対してのコンセプトである、ということです。
結
今回は、固有値、固有空間、固有多項式、固有方程式について解説しました。
その中で基礎的な部分をエクストリームに解説しました。
固有値に関する諸概念は線型代数を学ぶ上で避けては通れず、しかも数多の分野で使われます。
そして、今まで学習していた行列式やらの計算方法はある種、固有値を求めるために学んでいた、とも言えると思います(勿論、それだけじゃありませんが、1つの目標ということです)。
次回は、固有値、固有ベクトルの性質を使った線型代数における最重要(と思う)な対角化について解説します。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする