本記事の内容
本記事は行列の演算とその性質、行列の演算と転置の関係性について解説する記事です。
本記事を読むにあたり、「行列とは何か?」ということについて知っている必要があるため、以下の記事もあわせて御覧ください。
行列の演算
行列の演算にはスカラー倍と和とと積の4つが存在します。
「割り算は無いのかネ?」と思うかもしれませんが、行列を行列で割る、という割り算は考えません。
無理やり何か”行列同士の割り算”を定めることはできます(いくらでも)が、その演算に意味がありません。
しかし、行列の割り算に対応するものはあります。
それは次節で解説します。
行列の演算の前にベクトルの演算の復習
ここで注意なのが、前回(【線型代数学の基礎シリーズ】行列編 その1)で述べたように、行列はベクトルをたくさん並べたものと捉えることができます。
これから解説する行列の演算はベクトルの演算を一般化したものとなっていますので、ベクトルの演算を思い出しながら読むとより理解しやすいと思います。
ベクトルの演算についてはすでに高校数学で学んでいると思いますので、サラッと列挙するだけにしておきます。
ベクトルの演算
\(\displaystyle\boldsymbol{a}=\left(\begin{array}{c}a_1\\ a_2\\ \vdots \\a_m\end{array}\right)\)、\(\displaystyle\boldsymbol{b}=\left(\begin{array}{c}b_1\\ b_2\\ \vdots \\b_m\end{array}\right)\)とし、任意の自然数\(1\leq i\leq m\)に対して\(a_i,b_i\in\mathbb{C}\)(\(\mathbb{C}\)は複素数の集合)とする。
- スカラー倍 \(c\in\mathbb{C}\)に対して、\(c\boldsymbol{a}\)を $$ c\boldsymbol{a}=\left(\begin{array}{c}ca_1\\ ca_2\\ \vdots \\ca_m\end{array}\right) $$ をベクトル\(\boldsymbol{a}\)のスカラー倍という。
- 和、差 ベクトル\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の和\(\boldsymbol{a}+\boldsymbol{b}\)および差\(\boldsymbol{a}-\boldsymbol{b}\)を $$ \boldsymbol{a}+\boldsymbol{b}=\left(\begin{array}{c}a_1+b_1\\ a_2+b_2\\ \vdots \\a_m+b_m\end{array}\right),\quad \boldsymbol{a}-\boldsymbol{b}=\left(\begin{array}{c}a_1-b_1\\ a_2-b_2\\ \vdots \\a_m-b_m\end{array}\right) $$
- 内積 \(\boldsymbol{a}\)と\(\boldsymbol{b}\)の内積\((\boldsymbol{a},\boldsymbol{b})\)(または\(<\boldsymbol{a},\boldsymbol{b}>\)やら\(\boldsymbol{a}\cdot\boldsymbol{b}\)で表す)を $$ (\boldsymbol{a},\boldsymbol{b})=\sum_{i=1}^ma_ib_i=a_1b_1+a_2b_2+\dots+a_mb_m $$ で定める。この\((\boldsymbol{a},\boldsymbol{b})\)を\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の内積という。
行列のスカラー倍(定数倍)
簡単です。
というより予想通りといったところです。
行列のスカラー倍はベクトルのスカラー倍と同じで、行列のすべての成分をスカラー倍した行列がその行列のスカラー倍といいます。
これを行列の記号を用いて表すと、次です。
行列のスカラー倍 複素数\(c\)に対して、\((m,n)\)型行列\(A=(a_{ij})\)の各成分を\(c\)倍して得られる\((m,n)\)型行列を、\(A\)のスカラー倍または\(c\)倍といい、\(cA\)で表す。すなわち、 $$cA= \begin{pmatrix} ca_{11}&ca_{12}&\cdots &ca_{1n}\\ ca_{21}&ca_{22}&\cdots &ca_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ ca_{m1}&ca_{m2}&\cdots &ca_{mn}\\ \end{pmatrix} $$ で定める。より端的には\(cA=(ca_{ij})\)で定められる行列のことを\(A\)のスカラー倍または\(c\)倍という。特に、\(c=1\)の場合は\(cA\)を単に\(A\)で表し、\(c=-1\)の場合は\(cA\)を\(-A\)で表す。
要は、「行列を\(c\)倍しなさい」といわれたらば、行列のすべての要素を\(c\)倍するということです。
ここで、\(n=1\)としたとき、上記のベクトルのスカラー倍と一致していることが分かります。
(確かに一般化になっているネ)
行列のスカラー倍はどんな行列とどんな複素数に対しても定まります。
行列の和と差
これも予想通りといったところです。
行列の和、差もベクトルの和、差と同じす。
成分どうしを足し算、引き算するというのが行列の和、差です。
行列の和、差 2つの\((m,n)\)型行列\(A\)および\(B\)を、 $$ A= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}\\ \end{pmatrix},\quad B= \begin{pmatrix} b_{11}&b_{12}&\cdots &b_{1n}\\ b_{21}&b_{22}&\cdots &b_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ b_{m1}&b_{m2}&\cdots &b_{mn}\\ \end{pmatrix} $$ と書いたとする。
- 行列の和 \(A\)および\(B\)に対して、対応する成分の和を成分とする同じ型の行列を\(A\)と\(B\)の和といい、\(A+B\)で表す。すなわち、 $$ A+B= \begin{pmatrix} a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\ a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\\ \end{pmatrix} $$ を\(A\)と\(B\)の和という。
- 行列の和 \(A\)および\(B\)に対して、対応する成分の和を成分とする同じ型の行列を\(A\)と\(B\)の和といい、\(A+B\)で表す。すなわち、 $$ A-B= \begin{pmatrix} a_{11}-b_{11}&a_{12}-b_{12}&\cdots &a_{1n}-b_{1n}\\ a_{21}-b_{21}&a_{22}-b_{22}&\cdots &a_{2n}-b_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{m1}-b_{m1}&a_{m2}-b_{m2}&\cdots &a_{mn}-b_{mn}\\ \end{pmatrix} $$ を\(A\)と\(B\)の和という。
本質的には行列の差はスカラー倍を定めてしまえば、和から自ずと定まります。
というもの、行列の和\(A+B\)の\(B\)を\(-B\)とすれば良いからです。
さて、この和、差の場合も\(n=1\)とすることでベクトルの和、差と一致することが見て取れます。
ここで注意なのが、行列のスカラー倍はどんな行列、どんな複素数に対しても定まりましたが、和、差については同じ型同士の行列のみに定まります。
行列の積
これはスカラー倍と和、差に比べるとちょっとだけ複雑です。
まずは、どういうものかを明言してしまって、その後にベクトルの内積との関わりを述べたほうがわかりやすいと思うので、先に行列の積を明示します。
※ただ、ベクトルの内積を思い出しながら読むと「お?そういうことか?」となるかもしれませんので、思い出しながら読んでいただけると良いと思います。
とはいえ、「は?」となると思いますので、図も合わせてご覧ください。
行列の積 \(m,n,r\in\mathbb{N}\)に対して、\((m,n)\)型行列を\(A\)、\((n,r)\)型の\(B\)とし、 $$ A= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}\\ \end{pmatrix},\quad B= \begin{pmatrix} b_{11}&b_{12}&\cdots &b_{1r}\\ b_{21}&b_{22}&\cdots &b_{2r}\\ \vdots&\vdots& \ddots&\vdots\\ b_{n1}&b_{n2}&\cdots &b_{nr}\\ \end{pmatrix} $$ と書いたとする。このとき\(A\)と\(B\)の積\(AB\)を $$ AB=(c_{ij})=\sum_{h=1}^na_{ih}b_{hj}=a_{i1}b_{1j}+a_{i2}b_{2j}+\dots +a_{in}b_{nj} $$ で定める。すなわち、 \begin{eqnarray} AB&=& \begin{pmatrix} \displaystyle\sum_{h=1}^na_{1h}b_{h1}&\displaystyle\sum_{h=1}^na_{1h}b_{h2}&\cdots &\displaystyle\sum_{h=1}^na_{1h}b_{hr}\\ \displaystyle\sum_{h=1}^na_{2h}b_{h1}&\displaystyle\sum_{h=1}^na_{2h}b_{h2}&\cdots &\displaystyle\sum_{h=1}^na_{2h}b_{hr}\\ \vdots&\vdots& \ddots&\vdots\\ \displaystyle\sum_{h=1}^na_{mh}b_{h1}&\displaystyle\sum_{h=1}^na_{mh}b_{h2}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{hr}\\ \end{pmatrix}\\ &=&\begin{pmatrix} a_{11}b_{11}+a_{12}b_{21}+\cdots+a_{1n}b_{n1}&a_{11}b_{12}+a_{12}b_{22}+\cdots+a_{1n}b_{n2}&\cdots &a_{11}b_{1r}+a_{12}b_{2r}+\cdots+a_{1n}b_{nr}\\ a_{21}b_{11}+a_{22}b_{21}+\cdots+a_{2n}b_{n1}&a_{21}b_{12}+a_{22}b_{22}+\cdots+a_{2n}b_{n2}&\cdots &a_{21}b_{1r}+a_{22}b_{2r}+\cdots+a_{2n}b_{nr}\\ \vdots&\vdots& \ddots&\vdots\\ a_{m1}b_{11}+a_{m2}b_{21}+\cdots+a_{m1}b_{n1}&a_{m1}b_{12}+a_{m2}b_{22}\cdots+a_{mn}b_{n2}&\cdots &a_{m1}b_{1r}+a_{m2}b_{2r}+\cdots+a_{mn}b_{nr}\\ \end{pmatrix} \end{eqnarray}
「ナンジャコリャ(゜∀。)?」となると思います。
そこで模式図を描きます。
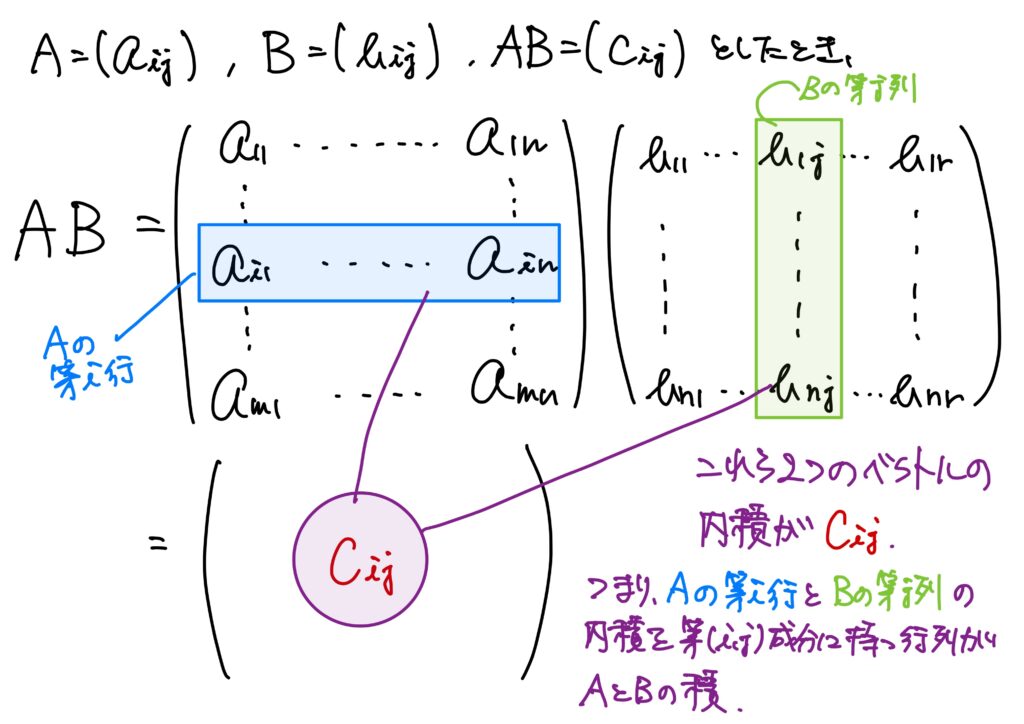
要するに、
ということなのです。
ここで注意なのが、\(AB\)は\((m,r)\)型の行列です。
つまり、
ということです。

すなわち、積\(AB\)が定まったとしても、必ずしも\(BA\)が定まるとは限らず、仮に\(BA\)が定まったとしても\(AB\)と等しくなるとも限らないわけです(勿論、\(AB=BA\)となる場合もあります)。
すでに内積と関係があるということを述べてしまいましたが、\(m=r=1\)の場合を考えてみると、
$$
A=(a_{11}\ a_{12}\ \cdots \ a_{1n}),\quad
B=
\left(
\begin{array}{c}
b_{11}\\
b_{21}\\
\vdots \\
b_{n1}
\end{array}\right)
$$
としたときに、
$$
AB=(a_{11}\ a_{12}\ \cdots \ a_{1n})\left(
\begin{array}{c}
b_{11}\\
b_{21}\\
\vdots \\
b_{n1}
\end{array}\right)=a_{11}b_{11}+a_{12}b_{21}+\dots +a_{1n}b_{n1}=\sum_{h=1}^na_{1h}b_{h1}
$$
となって、これはまさにベクトルの内積です。
行列の積には和、差よりも幾何的に(図形的に)意味を与えることができますが、それは線形変換の記事で解説しようと思います。
ここでは、「行列の掛け算ってこうやってやるんだぁ」と思っていただければ十分です。
いっちょ計算してみっか
やれ「内積だぜ!」といってもイメージが湧きにくいと思いますので、行列の積を実際に計算してみましょう。
ちなみに、筆者はかれこれ9年近く大学数学をやってきましたが、行列の積を計算するときは以下の図のように補助線を引いて、「どことどこの積を足して、どの成分になるのかな」ということを確認しながら計算しています。

では、実際に計算してみましょう!
例1.
$$
A=
\begin{pmatrix}
1&2\\
3&4
\end{pmatrix},\quad
B=
\begin{pmatrix}
5&6&7\\
8&9&10
\end{pmatrix},\quad
$$
としたとき、「\(A\)の行の数\(=\)\(B\)の列の数」が成り立つので、\(AB\)が計算でき、\(AB\)は\((2,3)\)型の行列になります。
\begin{eqnarray}
AB&=&
\begin{pmatrix}
1&2\\
3&4
\end{pmatrix}
\begin{pmatrix}
5&6&7\\
8&9&10
\end{pmatrix}\\
&=&
\begin{pmatrix}
1\times 5+2\times 8&1\times 6+2\times 9&1\times 7+2\times 10\\
3\times 5+4\times 8&3\times 6+4\times 9&3\times 7+4\times 10
\end{pmatrix}\\
&=&\begin{pmatrix}
5+16&6+18&7+20\\
15+32&18+36&21+40
\end{pmatrix}\\
&=&
\begin{pmatrix}
21&24&27\\
47&54&61
\end{pmatrix}
\end{eqnarray}
ここで、\(BA\)は計算できません。
なぜなら、\(B\)の行の数(\(=3\))と\(A\)の列の数(\(=2\))が一致していないためです。
先程も述べましたが、\(AB\)が計算できる(定まる)からといって\(BA\)が計算できる(定まる)とは限りません。
例えば、\(A\)と\(B\)の双方が\((m,m)\)型の正方行列であれば、\(AB\)も\(BA\)も定まります。
例2.
$$
C=
\begin{pmatrix}
1&2\\
3&4
\end{pmatrix},\quad
D=
\begin{pmatrix}
5&6\\
7&8
\end{pmatrix},\quad
$$
としたとき、「\(C\)の行の数\(=\)\(D\)の列の数」が成り立つので、\(CD\)が計算でき、\(CD\)は\((2,2)\)型の行列です。
また、「\(D\)の行の数\(=\)\(C\)の列の数」が成り立つので\(DC\)も計算でき、\(DC\)は\((2,2)\)型の行列です。
\begin{eqnarray}
CD&=&
\begin{pmatrix}
1&2\\
3&4
\end{pmatrix}
\begin{pmatrix}
5&6\\
7&8
\end{pmatrix}\\
&=&
\begin{pmatrix}
1\times5+2\times7&1\times 6+2\times8\\
3\times5+4\times7&3\times 6+4\times 8
\end{pmatrix}\\
&=&
\begin{pmatrix}
5+14&6+16\\
15+21&18+32
\end{pmatrix}\\
&=&
\begin{pmatrix}
19&22\\
36&50
\end{pmatrix}
\end{eqnarray}
\begin{eqnarray}
DC&=&
\begin{pmatrix}
5&6\\
7&8
\end{pmatrix}
\begin{pmatrix}
1&2\\
3&4
\end{pmatrix}\\
&=&
\begin{pmatrix}
5\times1+6\times3&5\times 2+4\times4\\
7\times1+8\times3&7\times 2+8\times 4
\end{pmatrix}\\
&=&
\begin{pmatrix}
5+18&10+16\\
7+24&14+32
\end{pmatrix}\\
&=&
\begin{pmatrix}
23&26\\
31&46
\end{pmatrix}
\end{eqnarray}
このように、\(CD\)および\(DC\)が定まったとしても、必ずしも\(CD\)と\(DC\)は等しくありません。
行列のスカラー倍、和、差、積の性質
行列のスカラー倍、和、差は比較的単純で、積については「ナンジャコリャ(゜∀。)?」というくらい複雑に見えたわけですが、結局どういう規則で複素数の計算をしているか、もっというと数の計算をしているかということです。
故に、数の計算で成り立つことと似たようなことが成り立ちます。
和、差の性質
定理3.(和、差の性質)
\(m,n\in\mathbb{N}\)とする。2つの\((m,n)\)型行列\(A\)および\(B\)に対して、以下が成り立つ。- \(A+B=B+A\quad\)(交換則)
- \((A+B)+C=A+(B+C)\quad\)(和の結合則)
- \(A+O=A\quad\)(\(O\)は\((m,n)\)型の零行列)
- \(A+(-A)=O\quad\)(\(O\)は\((m,n)\)型の零行列)
定理3.の証明
なんてことありません。
単に計算するだけです。
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix},\quad
B=
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix},\quad
C=
\begin{pmatrix}
c_{11}&\cdots &c_{1n}\\
\vdots& \ddots&\vdots\\
c_{m1}&\cdots &c_{mn}\\
\end{pmatrix}
$$
と書いたとします。
(1.(交換則)の証明)
$$
A+B=
\begin{pmatrix}
a_{11}+b_{11}&\cdots &a_{1n}+b_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}+b_{m1}&\cdots &a_{mn}+b_{mn}\\
\end{pmatrix}
$$
であり、
$$
B+A=
\begin{pmatrix}
b_{11}+a_{11}&\cdots &b_{1n}+a_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}+a_{m1}&\cdots &b_{mn}+a_{mn}\
\end{pmatrix}
$$
です。
ここで、
$$
(\forall i,j\in\mathbb{N};1\leq i\leq m,\ 1\leq j\leq n)\ a_{ij}+b_{ij}=b_{ij}+a_{ij}
$$
が成り立つため、\(A+B=B+A\)です。
(2.(和の結合則)の証明)
\begin{eqnarray}
(A+B)+C&=&
\left(
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}
\right)+
\begin{pmatrix}
c_{11}&\cdots &c_{1n}\\
\vdots& \ddots&\vdots\\
c_{m1}&\cdots &c_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}+b_{11}&\cdots &a_{1n}+b_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}+b_{m1}&\cdots &a_{mn}+b_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
c_{11}&\cdots &c_{1n}\\
\vdots& \ddots&\vdots\\
c_{m1}&\cdots &c_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}+b_{11}+c_{11}&\cdots &a_{1n}+b_{1n}+c_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}+b_{m1}+c_{m1}&\cdots &a_{mn}+b_{mn}+c_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
b_{11}+c_{11}&\cdots &b_{1n}+c_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}+c_{m1}&\cdots &b_{mn}+c_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}+\left(
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
c_{11}&\cdots &c_{1n}\\
\vdots& \ddots&\vdots\\
c_{m1}&\cdots &c_{mn}\\
\end{pmatrix}\right)\\
&=&A+(B+C)
\end{eqnarray}
となるので、成り立ちます。
(3.\(A+O=A\)の証明)
\((m,n)\)型の零行列を\(O\)とします。
すなわち、
$$
O=
\begin{pmatrix}
0&\cdots &0\\
\vdots& \ddots&\vdots\\
0&\cdots &0\\
\end{pmatrix}
$$
とします。
ただし、\(O\)は縦(すなわち行の数)に\(0\)が\(m\)個、横(すなわち列の数)に\(0\)が\(n\)個並んでいる行列です。
このとき、
\begin{eqnarray}
A+O&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
+
\begin{pmatrix}
0&\cdots &0\\
\vdots& \ddots&\vdots\\
0&\cdots &0\\
\end{pmatrix}
&=&
\begin{pmatrix}
a_{11}+0&\cdots &a_{1n}+0\\
\vdots& \ddots&\vdots\\
a_{m1}+0&\cdots &a_{mn}+0\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}=A
\end{eqnarray}
となって成り立ちます。
(4.\(A+(-A)=O\)の証明)
\begin{eqnarray}
A+(-A)&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
+
\begin{pmatrix}
-a_{11}&\cdots &-a_{1n}\\
\vdots& \ddots&\vdots\\
-a_{m1}&\cdots &-a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}-a_{11}&\cdots &a_{1n}-a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}-a_{m1}&\cdots &a_{mn}-a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
0&\cdots &0\\
\vdots& \ddots&\vdots\\
0&\cdots &0\\
\end{pmatrix}=O
\end{eqnarray}
となって成り立ちます。
定理3.の証明終わり
積の性質
定理4.(積の性質)
\(m,n,r,s\in\mathbb{N}\)とする。\((m,n)\)型行列\(A\)、\((n,r)\)型行列\(B\)、\((r,s)\)型行列\(C\)に対して、以下が成り立つ。- \((AB)C=A(BC)\quad\)(積の結合則)
- \(AI_n=I_mA=A\quad\)(\(I_n\)および\(I_m\)はそれぞれ\(n\)次、\(m\)次単位行列)
- \(AO_n=O_mA=O_{mn}\quad\) ただし、\(O_n\)は\(n\)次正方行列の零行列、\(O_m\)は\(m\)次正方行列の零行列、\(O_{mn}\)は\((m,n)\)型の零行列を指す。
この証明も単に計算するだけです。
余談(まじで読まなくてOK)
数式を書くソフトウェア(みたいなもの)として\(\LaTeX\)を使っているのですが、行列を\(\LaTeX\)で書こうとすると誠に骨が折れるんです。 疲れるんです。大変なんです。 \(\LaTeX\)を触ったことがある方には分かっていただけると思います。 加えて、\(\LaTeX\)でこういう文章を書くと、手汗と皮脂でキーボードがベタベタになりますよね。 (ちょっとだけでいいから労ってほしいなあ…と心の中の声をこぼしておく)では行きましょう。
定理4.の証明
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix},\quad
B=
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix},\quad
C=
\begin{pmatrix}
c_{11}&\cdots &c_{1s}\\
\vdots& \ddots&\vdots\\
c_{r1}&\cdots &c_{rs}\\
\end{pmatrix},\quad
$$
と書いたとします。
このとき、
\begin{eqnarray}
AB&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}b_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{hr}\\
\end{pmatrix}
\end{eqnarray}
となるため、
\(AB\)の第\((i,j)\)成分(\(i,j\)は\(1\leq i\leq m\)、\(1\leq j\leq r\)を満たす自然数)を\(e_{ij}\)で表したとすると、
$$
e_{ij}=\sum_{h=1}^na_{ih}b_{hj}
$$
と表されることに注意しておきます。
(1.積の結合則の証明)
まずは、\((AB)C\)と\(A(BC)\)が定まるのか、ということについて考えます。
\(A\)は\((m,n)\)型、\(B\)は\((n,r)\)型、\(C\)は\((r,s)\)型です。
故に、まず\(AB\)は\((m,r)\)型の行列として定まります。
次に\(AB\)と\(C\)の積ですが、\(AB\)は\((m,r)\)型、\(C\)は\((r,s)\)型ですので\((AB)C\)は\((m,s)\)型の行列として定まります。
さて、\(B\)は\((n,r)\)型、\(C\)は\((r,s)\)型ですので\(BC\)は\((n,s)\)型の行列として定まります。
また、\(A\)は\((m,n)\)型、\(BC\)は\((n,s)\)型ですので\(A(BC)\)は\((m,s)\)型の行列として定まります。
従って、\((AB)C\)も\(A(BC)\)も定まります。
\begin{eqnarray}
(AB)C&=&
\left(
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}\right)
\begin{pmatrix}
c_{11}&\cdots &c_{1s}\\
\vdots& \ddots&\vdots\\
c_{r1}&\cdots &c_{rs}\\
\end{pmatrix}
\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}b_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{hr}\
\end{pmatrix}
\begin{pmatrix}
c_{11}&\cdots &c_{1s}\\
\vdots& \ddots&\vdots\\
c_{r1}&\cdots &c_{rs}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle c_{11}\sum_{h=1}^na_{1h}b_{h1}+\dots +c_{r1}\sum_{h=1}^na_{1h}b_{hr} &\cdots &\displaystyle c_{1s}\sum_{h=1}^na_{1h}b_{h1}+\dots +c_{rs}\sum_{h=1}^na_{1h}b_{hr} \\
\vdots& \ddots&\vdots\\
\displaystyle c_{11}\sum_{h=1}^na_{mh}b_{h1}+\dots +c_{r1}\sum_{h=1}^na_{mh}b_{hr} &\cdots &\displaystyle c_{1s}\sum_{h=1}^na_{mh}b_{h1}+\dots +c_{rs}\sum_{h=1}^na_{mh}b_{hr} \\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle \sum_{k=1}^rc_{k1}\sum_{h=1}^na_{1h}b_{hk}&\cdots &\displaystyle \sum_{k=1}^rc_{ks}\sum_{h=1}^na_{1h}b_{hk}\\
\vdots& \ddots&\vdots\\
\displaystyle \sum_{k=1}^rc_{k1}\sum_{h=1}^na_{mh}b_{hk}&\cdots &\displaystyle \sum_{k=1}^rc_{ks}\sum_{h=1}^na_{mh}b_{hk}\\
\end{pmatrix}\\
\end{eqnarray}
この\((AB)C\)の第\((i,j)\)成分(\(i,j\)は\(1\leq i\leq s\)、\(1\leq j\leq s\)を満たす自然数)を\(d_{ij}\)で表したとすると、
\begin{eqnarray}
d_{ij}&=&\sum_{k=1}^rc_{kj}\sum_{h=1}^na_{ih}b_{hk}\\
&=&\sum_{k=1}^r\left(\sum_{h=1}^na_{ih}b_{hk}\right)c_{kj}\\
&=&\sum_{k=1}^r\sum_{h=1}^na_{ih}b_{hk}c_{kj}\\
\end{eqnarray}
です。
一方で、
\begin{eqnarray}
A(BC)&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\left(
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}
\begin{pmatrix}
c_{11}&\cdots &c_{1s}\\
\vdots& \ddots&\vdots\\
c_{r1}&\cdots &c_{rs}\\
\end{pmatrix}\right)
\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
\displaystyle\sum_{k=1}^rb_{1k}c_{k1}&\cdots &\displaystyle\sum_{k=1}^rb_{1k}c_{ks}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{k=1}^rb_{nk}c_{k1}&\cdots &\displaystyle\sum_{k=1}^rb_{nk}c_{ks}\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle a_{11}\sum_{k=1}^rb_{1k}c_{k1}+\dots +a_{1n}\sum_{k=1}^rb_{nk}c_{k1} &\cdots &\displaystyle a_{11}\sum_{k=1}^rb_{1k}c_{ks}+\dots +a_{1n}\sum_{k=1}^rb_{nk}c_{ks} \\
\vdots& \ddots&\vdots\\
\displaystyle a_{m1}\sum_{k=1}^rb_{1k}c_{k1}+\dots +a_{mn}\sum_{k=1}^rb_{nk}c_{k1} &\cdots &\displaystyle a_{m1}\sum_{k=1}^rb_{1k}c_{ks}+\dots +a_{mn}\sum_{k=1}^rb_{nk}c_{ks} \\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle \sum_{h=1}^na_{1h}\sum_{k=1}^rb_{hk}c_{k1}&\cdots &\displaystyle \sum_{h=1}^na_{1h}\sum_{k=1}^rb_{hk}c_{ks}\\
\vdots& \ddots&\vdots\\
\displaystyle \sum_{h=1}^na_{mk}\sum_{k=1}^rb_{hk}c_{k1}&\cdots &\displaystyle \sum_{h=1}^na_{mh}\sum_{k=1}^rb_{hk}c_{ks}\\
\end{pmatrix}\\
\end{eqnarray}
この\(A(BC)\)の第\((i,j)\)成分(\(i,j\)は\(1\leq i\leq s\)、\(1\leq j\leq s\)を満たす自然数)を\(d^\prime_{ij}\)で表したとすると、
\begin{eqnarray}
d^\prime_{ij}&=&\sum_{h=1}^na_{ih}\sum_{k=1}^rb_{hk}c_{kj}\\
&=&\sum_{h=1}^n\sum_{k=1}^ra_{ih}b_{hk}c_{kj}\\
&=&\sum_{k=1}^r\sum_{h=1}^na_{ih}b_{hk}c_{kj}\\
\end{eqnarray}
です。
従って、\(d_{ij}=d^\prime_{ij}\)により、積の結合則が成り立ちます。
(2.\(AI_n=I_nA=A\)の証明)
\(I_n\)を\(n\)次単位行列とします。
すなわち、\(I_n\)は\((n,n)\)型の正方行列で、
$$
I_n=
\begin{pmatrix}
1&0&\cdots &\cdots&0\\
0&1&0 &\cdots&0\\
\vdots&0& \ddots&\ddots&\vdots\\
\vdots&\vdots& \ddots&\ddots&0\\
0&\cdots&\cdots&0 &1\\
\end{pmatrix}
$$
とします。
このとき、
\begin{eqnarray}
AI_n&=&\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
1&0&\cdots &\cdots&0\\
0&1&0 &\cdots&0\\
\vdots&0& \ddots&\ddots&\vdots\\
\vdots&\vdots& \ddots&\ddots&0\\
0&\cdots&\cdots&0 &1\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}\times1+a_{12}\times0+\cdots+a_{1n}\times0&a_{11}\times0+a_{12}\times 1+\cdots+a_{1n}\times0&\cdots &a_{11}\times0+a_{12}\times0\cdots+a_{1n}\times1\\
a_{21}\times1+a_{22}\times0+\cdots+a_{2n}\times0&a_{21}\times0+a_{22}\times1+\cdots+a_{2n}\times0&\cdots &a_{21}\times0+a_{22}\times0+\cdots+a_{2n}\times1\\
\vdots&\vdots& \ddots&\vdots\\
a_{m1}\times1+a_{m2}\times0+\cdots+a_{m1}\times0&a_{m1}\times0+a_{m2}\times1+\cdots+a_{mn}\times0&\cdots &a_{m1}\times0+a_{m2}\times0+\cdots+a_{mn}\times1\\
\end{pmatrix}\\
&=&\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}=A
\end{eqnarray}
であり、
\begin{eqnarray}
I_nA&=&
\begin{pmatrix}
1&0&\cdots &\cdots&0\\
0&1&0 &\cdots&0\\
\vdots&0& \ddots&\ddots&\vdots\\
\vdots&\vdots& \ddots&\ddots&0\\
0&\cdots&\cdots&0 &1\\
\end{pmatrix}
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
1\times a_{11}+0\times a_{12}+\cdots+0\times a_{1n}&0\times a_{11}+1\times a_{12}+\cdots+0\times a_{1n}&\cdots &0\times a_{11}+0\times a_{12}\cdots+0\times a_{1n}\\
1\times a_{21}+0\times a_{22}+\cdots+0\times a_{2n}&0\times a_{21}+1\times a_{22}+\cdots+0\times a_{2n}&\cdots &0\times a_{21}+0\times a_{22}+\cdots+1\times a_{2n}\\
\vdots&\vdots& \ddots&\vdots\\
1\times a_{m1}+0\times a_{m2}+\cdots+0\times a_{m1}&0\times a_{m1}+1\times a_{m2}+\cdots+0\times a_{mn}&\cdots &a_{m1}\times0+a_{m2}\times0+\cdots+a_{mn}\times1\\
\end{pmatrix}\\
&=&\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}=A
\end{eqnarray}
ですので、証明完了です。
(3.\(AO_n=O_mA=O_{mn}\)の証明)
\(O_n\)を\(n\)次正方行列の零行列、\(O_m\)を\(m\)次正方行列の零行列、\(O_{mn}\)を\((m,n)\)型の零行列とします。
このとき、\(A\)は\((m,n)\)型なので、\(AO_n\)、\(O_mA\)が定まります。
また、行列の積から\(AO_n\)は\((m,n)\)型の行列、\(O_mA\)も\((m,n)\)型の行列です。
さて、
\begin{eqnarray}
AO_n&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
0&\cdots &0\\
\vdots&\ddots&\vdots\\
0&\cdots &0\\
\end{pmatrix}
\\
&=&
\begin{pmatrix}
a_{11}\times0+a_{12}\times0+\cdots+a_{1n}\times0&a_{11}\times0+a_{12}\times 0+\cdots+a_{1n}\times0&\cdots &a_{11}\times0+a_{12}\times0\cdots+a_{1n}\times0\\
a_{21}\times0+a_{22}\times0+\cdots+a_{2n}\times0&a_{21}\times0+a_{22}\times0+\cdots+a_{2n}\times0&\cdots &a_{21}\times0+a_{22}\times0+\cdots+a_{2n}\times0\\
\vdots&\vdots& \ddots&\vdots\\
a_{m1}\times0+a_{m2}\times0+\cdots+a_{m1}\times0&a_{m1}\times0+a_{m2}\times0+\cdots+a_{mn}\times0&\cdots &a_{m1}\times0+a_{m2}\times0+\cdots+a_{mn}\times0\\
\end{pmatrix}\\
&=&\begin{pmatrix}
0&\cdots &0\\
\vdots&\ddots&\vdots\\
0&\cdots &0\\
\end{pmatrix}=O_{mn}
\end{eqnarray}
一方、
\begin{eqnarray}
O_mA&=&
\begin{pmatrix}
0&\cdots &0\\
\vdots&\ddots&\vdots\\
0&\cdots &0\\
\end{pmatrix}
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\\
&=&
\begin{pmatrix}
0\times a_{11}+0\times a_{12}+\cdots+0\times a_{1n}&0\times a_{11}+0\times a_{12}+\cdots+0\times a_{1n}&\cdots &0\times a_{11}+0\times a_{12}\cdots+0\times a_{1n}\times1\\
0\times a_{21}+0\times a_{22}+\cdots+0\times a_{2n}&0\times a_{21}+0\times a_{22}+\cdots+0\times a_{2n}&\cdots &0\times a_{21}+0\times a_{22}+\cdots+0\times a_{2n}\\
\vdots&\vdots& \ddots&\vdots\\
0\times a_{m1}+0\times a_{m2}+\cdots+0\times a_{m1}&0\times a_{m1} +0\times a_{m2} +\cdots+0\times a_{mn} &\cdots &0\times a_{m1}+0\times a_{m2}+\cdots+0\times a_{mn}\\
\end{pmatrix}\\
&=&\begin{pmatrix}
0&\cdots &0\\
\vdots&\ddots&\vdots\\
0&\cdots &0\\
\end{pmatrix}=O_{mn}
\end{eqnarray}
定理4.の証明終わり
「折角\((i,j)\)成分の話をしたのだから、それを使えばいいんじゃない?」と思われるかもしれません。
勿論それで構いませんし、スマートです。
とはいえ、筆者としては実際に計算してみたほうが納得感があるので、今回はせっせと計算しています。
スカラー倍の性質
次にスカラー倍の性質です。
定理5.(スカラー倍の性質)
\(k,h\in\mathbb{C}\)、\(m,n,r\in\mathbb{N}\)とする。\((m,n)\)型行列\(A\)と\((n,r)\)型行列\(B\)と\(k,h\)に対して次が成り立つ。- \((kh)A=k(hA)\)
- \(k(AB)=(kA)B=A(kB)\)
- \(0A=O_{mn}\quad\)
- \(1A=A\)
これもまた計算するだけです。
定理5.の証明
\(k,h\in\mathbb{C}\)、\(m,n,r\in\mathbb{N}\)とします。
また、\(A\)を\((m,n)\)型の行列、\(B\)を\((n,r)\)型の行列とし、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix},\quad
B=
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}
$$
と書いたとします。
(1.\((kh)A=k(hA)\)の証明)
\begin{eqnarray}
(kh)A=
\begin{pmatrix}
kha_{11}&\cdots &kha_{1n}\\
\vdots& \ddots&\vdots\\
kha_{m1}&\cdots &kha_{mn}\\
\end{pmatrix},
\end{eqnarray}
であり、
\begin{eqnarray}
k(hA)=k
\begin{pmatrix}
ha_{11}&\cdots &ha_{1n}\\
\vdots& \ddots&\vdots\\
ha_{m1}&\cdots &ha_{mn}\\
\end{pmatrix}
=
\begin{pmatrix}
kha_{11}&\cdots &kha_{1n}\\
\vdots& \ddots&\vdots\\
kha_{m1}&\cdots &kha_{mn}\\
\end{pmatrix}
\end{eqnarray}
であるから、成り立ちます。
(2.\(k(AB)=(kA)B=A(kB)\)の証明)
\begin{eqnarray}
k(AB)&=&
k
\left(
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}
\right)
\\
&=&
k
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}b_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{hr}\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle k\sum_{h=1}^na_{1h}b_{h1}&\cdots &k \displaystyle\sum_{h=1}^na_{1h}b_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle k\sum_{h=1}^na_{mh}b_{h1}&\cdots &\displaystyle k\sum_{h=1}^na_{mh}b_{hr}\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle \sum_{h=1}^n(ka_{1h})b_{h1}&\cdots &\displaystyle\sum_{h=1}^n(ka_{1h})b_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle \sum_{h=1}^n(ka_{mh})b_{h1}&\cdots &\displaystyle \sum_{h=1}^n(ka_{mh})b_{hr}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle \sum_{h=1}^na_{1h}(kb_{h1})&\cdots &\displaystyle\sum_{h=1}^na_{1h}(kb_{hr})\\
\vdots& \ddots&\vdots\\
\displaystyle \sum_{h=1}^na_{mh}(kb_{h1})&\cdots &\displaystyle \sum_{h=1}^na_{mh}(kb_{hr})\\
\end{pmatrix}
\end{eqnarray}
これはまさに\(k(AB)=(kA)B=A(kB)\)を表しています。
(3.\(0A=O_{mn}\)の証明)
\begin{eqnarray}
0A&=&0
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
0\times a_{11}&\cdots &0\times a_{1n}\\
\vdots& \ddots&\vdots\\
0\times a_{m1}&\cdots &0\times a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
0&\cdots &0\\
\vdots&\ddots&\vdots\\
0&\cdots &0\\
\end{pmatrix}=O_{mn}
\end{eqnarray}
により、成り立ちます。
(4.\(1A=A\)の証明)
\begin{eqnarray}
1A&=&1
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
1\times a_{11}&\cdots &1\times a_{1n}\\
\vdots& \ddots&\vdots\\
1\times a_{m1}&\cdots &1\times a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}=A
\end{eqnarray}
により、成り立ちます。
定理5.の証明終わり
分配則
定理6.(分配則)
\(m,n,r\in\mathbb{N}\)、\(k,h\in\mathbb{C}\)とする。このとき、3つの行列\(C\)に対して、以下が成り立つ。- \(A\)が\((m,n)\)型、\(B\)及び\(C\)が\((n,r)\)型のとき、\(A(B+C)=AB+AC\)
- \(A\)と\(B\)が\((m,n)\)型、\(C\)が\((n,r)\)型のとき、\((A+B)C=AC+BC\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\(k(A+B)=kA+kB\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\((k+h)A=kA+hA\)
これも真正直に計算すればOKです。
定理6.の証明
\(m,n,r\in\mathbb{N}\)、\(k,h\in\mathbb{C}\)とします。
(1.\(A(B+C)=AB+AC\)の証明)
\(A\)を\((m,n)\)型、\(B\)と\(C\)が\((n,r)\)型の行列として、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix},\quad
B=
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix},\quad
C=
\begin{pmatrix}
c_{11}&\cdots &c_{1n}\\
\vdots& \ddots&\vdots\\
c_{m1}&\cdots &c_{mn}\\
\end{pmatrix}
$$
と書いたとします。
このとき、
\begin{eqnarray}
A(B+C)&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\left(
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}+
\begin{pmatrix}
c_{11}&\cdots &c_{1n}\\
\vdots& \ddots&\vdots\\
c_{m1}&\cdots &c_{mn}\\
\end{pmatrix}
\right)\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
b_{11}+c_{11}&\cdots &b_{1r}+c_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}+c_{n1}&\cdots &b_{nr}+c_{nr}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}(b_{h1}+c_{h1})&\cdots &\displaystyle\sum_{h=1}^na_{1h}(b_{hr}+c_{hr})\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}(b_{h1}+c_{h1})&\cdots &\displaystyle\sum_{h=1}^na_{mh}(b_{hr}+c_{hr})
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^n(a_{1h}b_{h1}+a_{1h}c_{h1})&\cdots &\displaystyle\sum_{h=1}^n(a_{1h}b_{hr}+a_{1h}c_{hr})\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^n(a_{mh}b_{h1}+a_{mh}c_{h1})&\cdots &\displaystyle\sum_{h=1}^n(a_{mh}b_{hr}+a_{mh}c_{hr})
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}b_{h1}+\sum_{h=1}^na_{1h}c_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}b_{hr}+\sum_{h=1}^na_{1h}c_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}b_{h1}+\sum_{h=1}^na_{mh}c_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{hr}+\sum_{h=1}^na_{mh}c_{hr}
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}b_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{hr}
\end{pmatrix}+
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}c_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}c_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}c_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}c_{hr}
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}+
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
c_{11}&\cdots &c_{1n}\\
\vdots& \ddots&\vdots\\
c_{m1}&\cdots &c_{mn}\\
\end{pmatrix}\\
&=&AB+AC
\end{eqnarray}
となるので、成り立ちます。
(2.\((A+B)C=AC+BC\)の証明)
\(A\)と\(B\)が\((m,n)\)型、\(C\)が\((n,r)\)型の行列として、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix},\quad
B=
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix},\quad
C=
\begin{pmatrix}
c_{11}&\cdots &c_{1r}\\
\vdots& \ddots&\vdots\\
c_{n1}&\cdots &c_{nr}\\
\end{pmatrix}
$$
と書いたとします。
このとき、
\begin{eqnarray}
(A+B)C&=&
\left(
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}
\right)
\begin{pmatrix}
c_{11}&\cdots &c_{1r}\\
\vdots& \ddots&\vdots\\
c_{n1}&\cdots &c_{nr}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}+b_{11}&\cdots &a_{1n}+b_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}+b_{m1}&\cdots &a_{mn}+b_{mn}\\
\end{pmatrix}
\begin{pmatrix}
c_{11}&\cdots &c_{1r}\\
\vdots& \ddots&\vdots\\
c_{n1}&\cdots &c_{nr}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^n(a_{1h}+b_{1h})c_{h1}&\cdots &\displaystyle\sum_{h=1}^n(a_{1h}+b_{1h})c_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^n(a_{mh}+b_{mh})c_{h1}&\cdots &\displaystyle\sum_{h=1}^n(a_{mh}+b_{mh})c_{hr}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^n(a_{1h}c_{h1}+b_{1h}c_{h1})&\cdots &\displaystyle\sum_{h=1}^n(a_{1h}c_{hr}+b_{1h}c_{hr})\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^n(a_{mh}c_{h1}+b_{mh}c_{h1})&\cdots &\displaystyle\sum_{h=1}^n(a_{mh}c_{hr}+b_{mh}c_{hr})\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}c_{h1}+\sum_{h=1}^nb_{1h}c_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}c_{hr}+\sum_{h=1}^nb_{1h}c_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}c_{h1}+\sum_{h=1}^nb_{mh}c_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}c_{hr}+\sum_{h=1}^nb_{mh}c_{hr}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}c_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}c_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}c_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}c_{hr}\\
\end{pmatrix}+
\begin{pmatrix}
\displaystyle\sum_{h=1}^nb_{1h}c_{h1}&\cdots &\displaystyle\sum_{h=1}^nb_{1h}c_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^nb_{mh}c_{h1}&\cdots &\displaystyle\sum_{h=1}^nb_{mh}c_{hr}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
c_{11}&\cdots &c_{1r}\\
\vdots& \ddots&\vdots\\
c_{n1}&\cdots &c_{nr}\\
\end{pmatrix}+
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}
\begin{pmatrix}
c_{11}&\cdots &c_{1r}\\
\vdots& \ddots&\vdots\\
c_{n1}&\cdots &c_{nr}\\
\end{pmatrix}\\
&=&AC+BC
\end{eqnarray}
となるので、成り立ちます。
(3.\(k(A+B)=kA+kB\)の証明)
\(k\in\mathbb{C}\)として、\(A\)と\(B\)が共に\((m,n)\)型の行列だとして、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix},\quad
B=
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}
$$
と書いたとします。
このとき、
\begin{eqnarray}
k(A+B)&=&
k\left(
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}
\right)\\
&=&k
\begin{pmatrix}
a_{11}+b_{11}&\cdots &a_{1n}+b_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}+b_{m1}&\cdots &a_{mn}+b_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
k(a_{11}+b_{11})&\cdots &k(a_{1n}+b_{1n})\\
\vdots& \ddots&\vdots\\
k(a_{m1}+b_{m1})&\cdots &k(a_{mn}+b_{mn})\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
ka_{11}+kb_{11}&\cdots &ka_{1n}+kb_{1n}\\
\vdots& \ddots&\vdots\\
ka_{m1}+kb_{m1}&\cdots &ka_{mn}+kb_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
ka_{11}&\cdots &ka_{1n}\\
\vdots& \ddots&\vdots\\
ka_{m1}&\cdots &ka_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
kb_{11}&\cdots &kb_{1n}\\
\vdots& \ddots&\vdots\\
kb_{m1}&\cdots &kb_{mn}\\
\end{pmatrix}\\
&=&
k\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}+
k\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}\\
&=&kA+kB
\end{eqnarray}
となるので、成り立ちます。
(4.\((k+h)A=kA+hA\)の証明)
\(A\)を\((m,n)\)型の行列とし、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
$$
と書いたとします。
このとき、複素数\(k,h\)に対して、
\begin{eqnarray}
(k+h)A&=&
(k+h)
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
(k+h)a_{11}&\cdots &(k+h)a_{1n}\\
\vdots& \ddots&\vdots\\
(k+h)a_{m1}&\cdots &(k+h)a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
ka_{11}+ha_{11}&\cdots &ka_{1n}+ha_{1n}\\
\vdots& \ddots&\vdots\\
ka_{m1}+ha_{m1}&\cdots &ka_{mn}+ha_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
ka_{11}&\cdots &ka_{1n}\\
\vdots& \ddots&\vdots\\
ka_{m1}&\cdots &ka_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
ha_{11}&\cdots &ha_{1n}\\
\vdots& \ddots&\vdots\\
ha_{m1}&\cdots &ha_{mn}\\
\end{pmatrix}\\
&=&
k\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}+
h\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}\\
&=&kA+hA
\end{eqnarray}
となって成り立ちます。
定理6.の証明終わり
いや〜長かったですねえ。
とはいえ、ほとんどの書籍は積の結合則以外は「明らかなので証明は省略」として証明を与えてないものが多い印象があります。
まあ、正直明らかといえば明らかなのですが、個人的には何度か言っていますが、「明らか」かどうかは人によるし、証明が省略されているということは証明されていないのと同じわけですから、証明されていない事実を使うというのは筆者の性に合わないのです。
この節のまとめ
さて、事実が乱立していたのでこれまでの話を1つの定理として明示しておきます。
定理.(和、差、積、スカラー倍の性質、分配法則)
\(k,h\in\mathbb{C}\)とし、\(m,n,r,s\in\mathbb{N}\)とする。- 和、差の性質 2つの\((m,n)\)型行列\(A\)および\(B\)に対して、以下が成り立つ。
- \(A+B=B+A\quad\)(交換則)
- \((A+B)+C=A+(B+C)\quad\)(和の結合則)
- \(A+O=A\quad\)(\(O\)は\((m,n)\)型の零行列)
- \(A+(-A)=O\quad\)(\(O\)は\((m,n)\)型の零行列)
- 積の性質 \((m,n)\)型行列\(A\)、\((n,r)\)型行列\(B\)、\((r,s)\)型行列\(C\)に対して、以下が成り立つ。
- \((AB)C=A(BC)\quad\)(積の結合則)
- \(AI_n=I_nA=A\quad\)(\(I_n\)は\(n\)次単位行列)
- \(AO_n=O_mA=O_{mn}\quad\) ただし、\(O_n\)は\(n\)次正方行列の零行列、\(O_m\)は\(m\)次正方行列の零行列、\(O_{mn}\)は\((m,n)\)型の零行列を指す。
- スカラー倍の性質 \(k,h\in\mathbb{C}\)と\((m,n)\)型行列\(A\)と\((n,r)\)型行列\(B\)に対して次が成り立つ。
- \((kh)A=k(hA)\)
- \(k(AB)=(kA)B=A(kB)\)
- \(0A=O_{mn}\quad\)
- \(1A=A\)
- 分配則 \(k,h\in\mathbb{C}\)と3つの行列\(A\)、\(B\)、\(C\)に対して次が成り立つ。
- \(A\)が\((m,n)\)型、\(B\)及び\(C\)が\((n,r)\)型のとき、\(A(B+C)=AB+AC\)
- \(A\)と\(B\)が\((m,n)\)型、\(C\)が\((n,r)\)型のとき、\((A+B)C=AC+BC\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\(k(A+B)=kA+kB\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\((k+h)A=kA+hA\)
次に行列の演算と転置の関係性を見ていきます。
行列の演算と転置
行列の転置は、一言で言えば「行と列を入れ替えた行列ですよ〜」という話をしていました。
サラッとチャラく復習すると、
転置行列 \((m,n)\)行列\(A=(a_{ij})\)に対して、行と列を入れ替えた行列を\(A\)の転置行列といい、\(A^\top\)や\(^t\!A\)で表す。 すなわち、\(A=(a_{ij})\)を $$ A= \begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots&\vdots& \ddots&\vdots\\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix} $$ と書いたとき、\(^t\!A=(a_{ji})\)を、つまり $$^t\!A=A^\top= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1m}\\ a_{21}&a_{22}&\cdots &a_{2m}\\ \vdots&\vdots& \ddots&\vdots\\ a_{n1}&a_{m2}&\cdots &a_{nm}\\ \end{pmatrix}$$ を\(A\)の転置行列という。
でした。
行列の演算とこの転置の関係性、つまり転置行列が含まれるような行列の演算の性質について解説します。
定理7.(転置行列を含む行列の演算の性質)
\(k\in\mathbb{C}\)、\(m,n,r\in\mathbb{N}\)とし、行列\(A\)、\(B\)、\(k\)に対して、以下が成り立つ。- \(A\)が\((m,n)\)型の行列のとき、すなわち任意の行列に対して、\(\left(A^\top\right)^\top=A\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\(\left(A+B\right)^\top=A^\top+B^\top\)
- \(A\)が\((m,n)\)型、\(B\)が\((n,r)\)型のとき、\((AB)^\top=B^\top A^\top\quad\)(順番に注意)
- \(A\)が\((m,n)\)型の行列のとき、すなわち任意の行列に対して、\((kA)^\top=kA^\top\)
この証明も真正直に計算すればOKです。
定理7.の証明
(1.\(^t!\left(^t!A\right)=A\)の証明)
\(A\)を\((m,n)\)型の行列とし、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
$$
と書いたとします。
このとき、
\begin{eqnarray}
\left(A^\top\right)^\top&=&
\left(\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}^\top\right)^\top
=
\begin{pmatrix}
a_{11}&\cdots &a_{m1}\\
\vdots& \ddots&\vdots\\
a_{1n}&\cdots &a_{mn}\\
\end{pmatrix}^\top
=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}=A
\end{eqnarray}
となって、成り立ちます。
(2.\((A+B)^\top=A^\top+B^\top\)の証明)
\(A\)および\(B\)が共に\((m,n)\)型の行列とし、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix},\quad
B=
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}
$$
と書いたとします。
このとき、
\begin{eqnarray}
(A+B)^\top&=&
\left(
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}
\right)^\top\\
&=&
\begin{pmatrix}
a_{11}+b_{11}&\cdots &a_{1n}+b_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}+b_{m1}&\cdots &a_{mn}+b_{mn}\\
\end{pmatrix}^\top\\
&=&
\begin{pmatrix}
a_{11}+b_{11}&\cdots &a_{m1}+b_{m1}\\
\vdots& \ddots&\vdots\\
a_{1n}+b_{1n}&\cdots &a_{mn}+b_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{m1}\\
\vdots& \ddots&\vdots\\
a_{1n}&\cdots &a_{mn}\\
\end{pmatrix}+
\begin{pmatrix}
b_{11}&\cdots &b_{m1}\\
\vdots& \ddots&\vdots\\
b_{1n}&\cdots &b_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}^\top+
\begin{pmatrix}
b_{11}&\cdots &b_{1n}\\
\vdots& \ddots&\vdots\\
b_{m1}&\cdots &b_{mn}\\
\end{pmatrix}^\top\\
&=&A^\top+B^\top
\end{eqnarray}
となるので、成り立ちます。
(3.\((AB)^\top=B^\top A^\top\)の証明)
\(A\)を\((m,n)\)型、\(B\)を\((n,r)\)型の行列とし、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix},\quad
B=
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}
$$
と書いたとします。
このとき、
\begin{eqnarray}
(AB)^\top&=&
\left(
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}
\right)^\top\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{1h}b_{hr}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{mh}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{hr}
\end{pmatrix}
^\top\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^na_{1h}b_{h1}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{h1}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^na_{1h}b_{hr}&\cdots &\displaystyle\sum_{h=1}^na_{mh}b_{hr}
\end{pmatrix}
\end{eqnarray}
です。
一方、
\begin{eqnarray}
B^\top A^\top&=&
\begin{pmatrix}
b_{11}&\cdots &b_{1r}\\
\vdots& \ddots&\vdots\\
b_{n1}&\cdots &b_{nr}\\
\end{pmatrix}^\top
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}^\top\\
&=&
\begin{pmatrix}
b_{11}&\cdots &b_{n1}\\
\vdots& \ddots&\vdots\\
b_{1r}&\cdots &b_{nr}\\
\end{pmatrix}
\begin{pmatrix}
a_{11}&\cdots &a_{m1}\\
\vdots& \ddots&\vdots\\
a_{1n}&\cdots &a_{mn}\\
\end{pmatrix}\\
&=&
\begin{pmatrix}
\displaystyle\sum_{h=1}^nb_{h1}a_{1h}&\cdots &\displaystyle\sum_{h=1}^nb_{h1}a_{mh}\\
\vdots& \ddots&\vdots\\
\displaystyle\sum_{h=1}^nb_{hr}a_{1h}&\cdots &\displaystyle\sum_{h=1}^nb_{hr}a_{mh}
\end{pmatrix}
\end{eqnarray}
となるから、\((AB)^\top=B^\top A^\top\)が成り立ちます。
(4.\((kA)^\top=kA^\top\)の証明)
\(k\in\mathbb{C}\)、\(A\)を\((m,n)\)型の行列とし、
$$
A=
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
$$
と書いたとします。
このとき、
\begin{eqnarray}
(kA)^\top&=&
\left(k
\begin{pmatrix}
a_{11}&\cdots &a_{1n}\\
\vdots& \ddots&\vdots\\
a_{m1}&\cdots &a_{mn}\\
\end{pmatrix}
\right)^\top\\
&=&
\begin{pmatrix}
ka_{11}&\cdots &ka_{1n}\\
\vdots& \ddots&\vdots\\
ka_{m1}&\cdots &ka_{mn}\\
\end{pmatrix}
^\top\\
&=&
\begin{pmatrix}
ka_{11}&\cdots &ka_{m1}\\
\vdots& \ddots&\vdots\\
ka_{1n}&\cdots &ka_{mn}\\
\end{pmatrix}\\
&=&
k\begin{pmatrix}
a_{11}&\cdots &a_{m1}\\
\vdots& \ddots&\vdots\\
a_{1n}&\cdots &a_{mn}\\
\end{pmatrix}\\
&=&kA^\top
\end{eqnarray}
となるので、成り立ちます。
定理7.の証明終わり
結
今回は、行列の和、差、積、スカラー倍について解説し、その演算の性質を証明しました。
また、転置行列が含まれる演算の諸性質も解説しました。
誠に長丁場だったかと思いますが、実は本記事で扱った内容は量が多いだけで難易度は高ありません。
ただ、行列の積については添字やらなんやらで頭がこんがらがることがありますので難易度はちょっと高めです。
行列の和、差、スカラー倍、積ともにベクトルの演算の一般化となっていました。
積については、今まで扱ってきた実数とちょっと違って、行列の積\(AB\)と\(BA\)は必ずしも定められるわけではなく、仮に定まったとしても必ずしも一致ないということに注意してください。
次回は「正則行列と逆行列」「それらの基本的な性質」について解説します。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする