本記事の内容
本記事は、極大値と極小値とは何か、ロル(ロル)の定理のイメージとその証明を説明する記事です。
本記事を読むにあたり、微分係数について知っている必要があるため、以下の記事も合わせて御覧ください。
極値(極大値、極小値)
極大値、極小値のイメージとその数学的な説明
極値は高校数学で三次関数の単元で出現したと思います。
そのイメージを思い出すと、三次関数に対して、
というような説明で学習したかと思います。
図で描くとこんな感じでした。
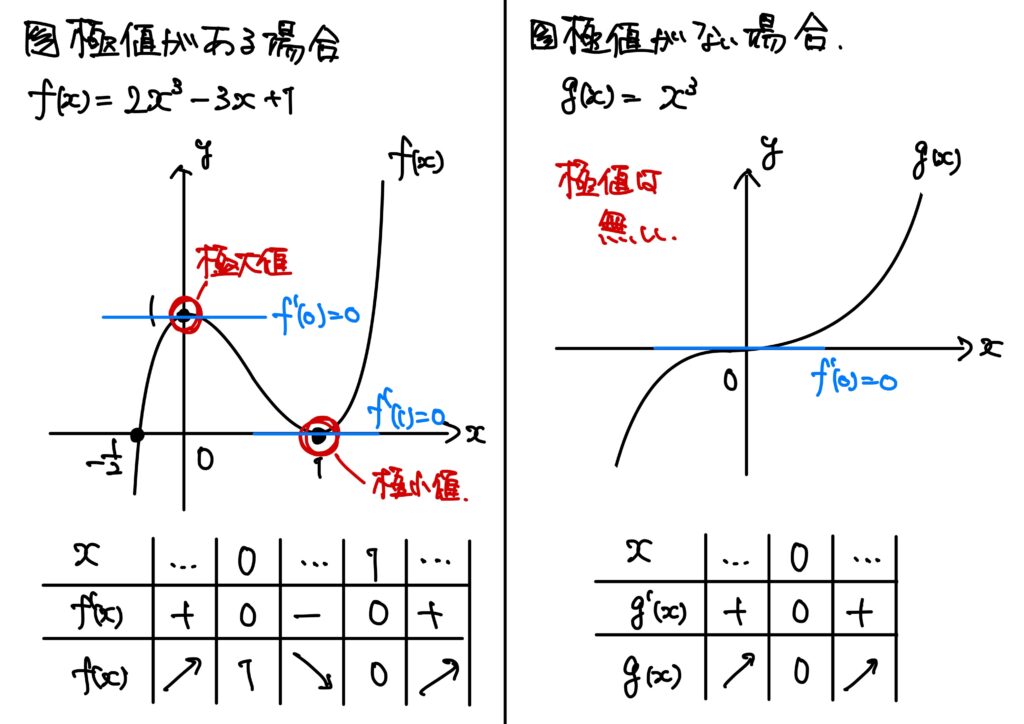
故に、極値が複数あることもあります。
しかし、この説明だと「\(f\)はある範囲で微分可能である。」という仮定が必要になります。
そもそも微分可能でなければ\(f^\prime(x)=0\)という方程式が解けないどころか\(f^\prime(x)\)が存在するかどうか分かりません。
本来極値は微分可能かどうかということには依存しません。
つまり、微分可能でないような関数に対しても極値というのは存在します。
例えば、以下のようなカクカクしている関数にも極値は存在します。
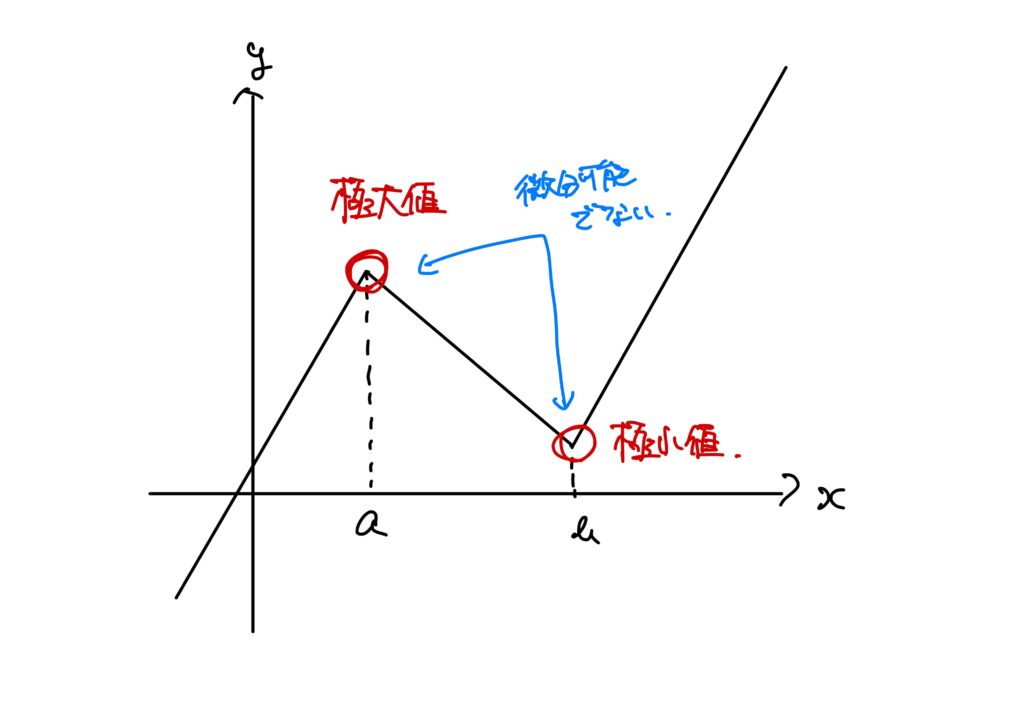
故に、上記の
という説明は微分可能な関数の場合については説明できているのですが、微分可能でない場合の極値については説明していないことになります。
よって、もっと一般的に(微分可能でない場合も含めた)極値、すなわち極大値と極小値とは何か、ということについて説明します。
とはいえ、イメージとしては同じです。
直感的には、
- \(f(c)\)が\(c\)に十分近い範囲で、\(f\)の最大値になっているときに、\(f(c)\)は極大値という。
- \(f(c)\)が\(c\)に十分近い範囲で、\(f\)の最小値になっているときに、\(f(c)\)は極小値という。
ということです。
これを数学的に書くと以下になります。
- 極大値 \(f(c)\)が\(c\)に十分近い範囲で、\(f\)の最大値になっているとき、すなわち $$ (\exists \epsilon>0)\ {\rm s.t.}\ (\forall x\in I:|x-c|<\epsilon)\ f(c)\geq f(x) $$ が成り立っているとき、\(f(c)\)は\(f\)の極大値という。
- 極小値 \(f(c)\)が\(c\)に十分近い範囲で、\(f\)の最小値になっているとき、すなわち $$ (\exists \epsilon>0)\ {\rm s.t.}\ (\forall x\in I:|x-c|<\epsilon)\ f(c)\leq f(x) $$ が成り立っているとき、\(f(c)\)は\(f\)の極小値という。

ここで、注意ですが、極大値と最大値、極小値と最小値は一致することもあります。
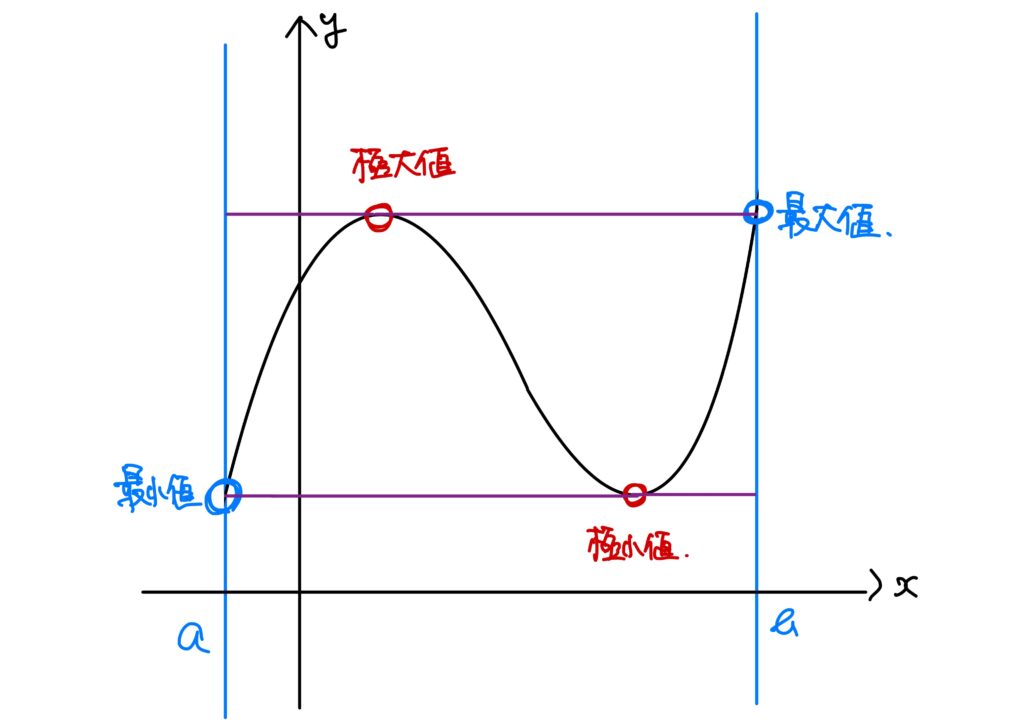
しかし、極大値だからといって最大値とは限りませんし、極小値だからといって最小値とも限りません。
さらに言えば、最大値だからといって極大値は限りませんし、最小値だからといって極小値とも限りません。
極値の性質
極値の説明の際に、最初に高校数学では
というような説明で習いましたよね〜という話をしました。
しかしこれは「微分可能っていう仮定が必要になっちゃってるよね〜」という話もしました。
とはいえ、この高校数学的な説明が間違っているわけではありません。
主張としては正しいです。
ただ、極値の説明としては不十分だ、という話です。
なぜ正しいのか、ということは次の事実が成り立つからです。
要するに、「極値点での微分係数は\(0\)でござんす。」というわけです。
この命題の証明を与えます。
命題1.の証明
まずは、\(f\)が\(c\)で極大値をとる場合を考えます。
※極小値の場合も同様です。
すなわち、
$$
(\exists \epsilon>0)\ {\rm s.t.}\ (\forall x\in I:|x-c|<\epsilon)\ f(c)\geq f(x)
$$
が成り立っているとします。
このとき、\(|h|<\epsilon\)であれば、\(|h-c|<\epsilon\)ですので、
$$
f(c+h)-f(c)\leq 0
$$
です。
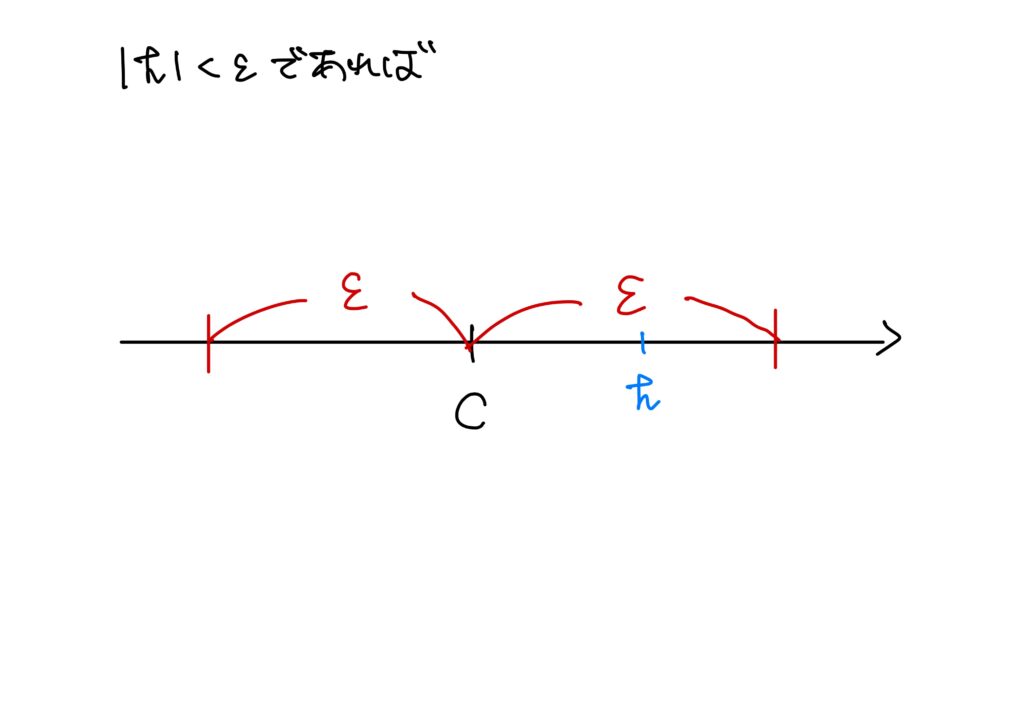
このとき、\(h>0\)であれば、\(h\neq 0\)ですので、
$$
\frac{f(c+h)-f(c)}{h}\leq 0
$$
です。
故に、ここで\(h\to+0\)とすると、\(f^\prime(c)\leq0\)です。
一方、\(h<0\)であれば、\(h\neq 0\)ですので、
$$
\frac{f(c+h)-f(c)}{h}\geq 0
$$
です。
故に、ここで\(h\to-0\)とすると、\(f^\prime(c)\geq0\)です。
従って、\(f^\prime(c)\leq0\)かつ\(f^\prime(c)\geq0\)ですので、\(f^\prime(c)=0\)です。
次に、\(f\)が\(c\)で極小値をとる場合を考えます。
すなわち、
$$
(\exists \epsilon>0)\ {\rm s.t.}\ (\forall x\in I:|x-c|<\epsilon)\ f(c)\leq f(x)
$$
が成り立っているとします。
このとき、\(|h|<\epsilon\)であれば、\(|h-c|<\epsilon\)ですので、
$$
f(c+h)-f(c)\geq 0
$$
です。
このとき、\(h>0\)であれば、\(h\neq 0\)ですので、
$$
\frac{f(c+h)-f(c)}{h}\geq 0
$$
です。
故に、ここで\(h\to+0\)とすると、\(f^\prime(c)\geq0\)です。
一方、\(h<0\)であれば、\(h\neq 0\)ですので、
$$
\frac{f(c+h)-f(c)}{h}\leq 0
$$
です。
故に、ここで\(h\to-0\)とすると、\(f^\prime(c)\leq0\)です。
従って、\(f^\prime(c)\leq0\)かつ\(f^\prime(c)\geq0\)ですので、\(f^\prime(c)=0\)です。
以上のことから、\(f\)が\(c\)で極大値を取ろうが、極小値を取ろうが\(f^\prime(c)=0\)が導けました。
ちなみに、「”\(c\)が\(I\)の内点である”という条件を使って無くね?」と思うかもしれませんが、暗に使っています。
というもの、\(f(c+h)\)を考えるときに使っています。
もし仮に\(c\)が\(I\)の内点でなければ、つまり、\(c\)が\(I\)の外側や端っこの点だったときを考えてみます。
\(c\)が\(I\)の外側だったらそもそも定義域外なので、\(f\)の\(c\)での値\(f(c)\)は存在しません。
\(c\)が\(I\)の端っこの点であれば、\(c+h\)が\(I\)の外側に出てしまう可能性があるのでこの場合もダメです。
従って、\(f(c+h)\)という値の存在を担保するために\(c\)は\(I\)の内点である、という条件が必要になります。
証明終わり
次にロルの定理を説明し、証明します。
ロルの定理
ロルの定理は平均値の定理(後の記事で解説します)の証明に必要な事実になります。
また、ロルの定理はワイエルシュトラスの最大値定理(【解析学の基礎シリーズ】関数の極限編 その16)から導けます。
さて、まずはロルの定理のイメージからいきましょう。
ロルの定理のイメージ
なんてことありません。
「当然じゃね?」となる方も多いと思います(かくいう筆者もそう思います)。
ロルの定理を平たく言えば、
ということです。
文章で書かれても「は?」となるかもしれませんので、図で説明します。

このように、途切れること無く\(f(a)\)と\(f(b)\)を滑らかに(微分可能であるという条件)つないだとき、つないだ線には必ず極値を取りまっせ、ということです。
先程も述べましたが、筆者はロルの定理を初めて見たときに「当然じゃね?」と思いました。
そういう意味ではワイエルシュトラスの最大値定理や中間値の定理を初めて見たときと感覚が似ています。
では、ロルの定理を数学的に明示して、証明しましょう!
ロルの定理の明示とその証明
ロルの定理を明示します。
この定理の証明にはワイエルシュトラスの最大値定理を使います。
ワイエルシュトラスの最大値定理は何だったか、というと、次でした。
ワイエルシュトラスの最大値定理の証明は【解析学の基礎シリーズ】関数の極限編 その16を御覧ください。
では、証明に入りましょう。
ロルの定理の証明
\(f:I=[a,b]\to\mathbb{R}\)は連続で、\((a,b)\)で微分可能、\(f(a)=f(b)\)が成り立つとします。
目標は、\(f^\prime(c)=0\)を満たすような\(c\in(a,b)\)を見つけてくることです。
今、\(f:I\to\mathbb{R}\)は連続ですのでワイエルシュトラスの最大値定理の仮定を満たします。
従って、\(f\)は\(I=[a,b]\)で最大値と最小値を取ります。
仮に、最大値と最小値が等しければ、\(f\)は定数関数です。
実際、\(f\)は\(I\)で最大値と最小値を取るので、
$$
(\exists c\in[a,b])\ {\rm s.t.}\ (\forall x\in [a,b])\ f(c)\geq f(x)\land f(c)\leq f(x)
$$
が成り立ちます。
すなわち、
$$
(\exists c\in[a,b])\ {\rm s.t.}\ (\forall x\in [a,b])\ f(c)=f(x)
$$
です。
\(f(c)\)は定数ですので、これはまさに\(f\)が定数関数であることを指しています。
従って、最大値と最小値が一致していれば、\(f\)は定数関数ですので、\(\displaystyle c=\frac{a+b}{2}\)とすれば、\(c\in(a,b)\)かつ\(f^\prime(c)=0\)です。
次に、最大値と最小値が等しくない場合を考えます。
この場合、最大値と最小値のうち、少なくとも一方は\(f(a)=f(b)\)と等しくありません。
すなわち、\([a,b]\)の端点\(a,b\)でない\([a,b]\)の点(\(a,b\)の中の点)、いわば\(I\)のある内点\(c\)が存在して、\(c\)で\(f\)は最大値かまたは最小値を取ることになります。
より噛み砕いて言えば、
①\(f\)の最大値が\(f(a)=f(b)\)と等しくなく、最小値が\(f(a)=f(b)\)と等しい場合

②\(f\)の最大値が\(f(a)=f(b)\)と等しく、最小値が\(f(a)=f(b)\)と等しくない場合

③\(f\)の最大値と最小値のどちらも\(f(a)=f(b)\)と等しくない場合
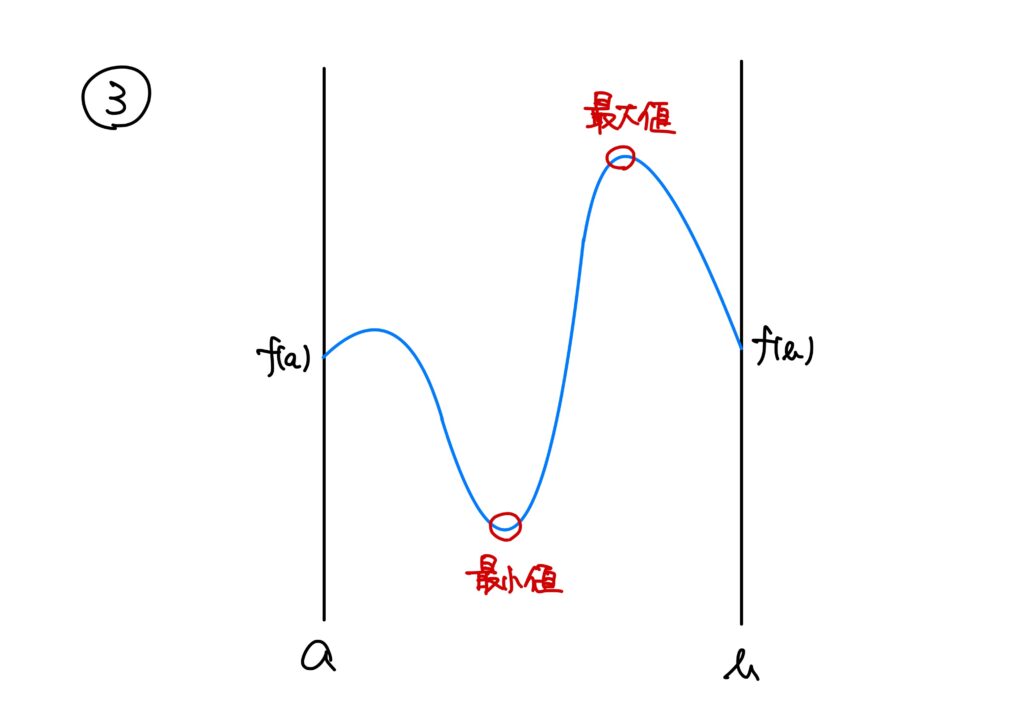
いずれも場合でも、\(I\)の内点\(c\)で最大値か最小値を取ることになります。
この場合、最大値は極大値に、最小値は極小値に一致します。
これは直感的にも分かりますが少々言及しておきます。
\(c\in(a,b)\)で最大値\(f(c)\)を取る場合、\(f(c)\)は\(I\)での最大値ですので、
$$
(\forall x\in I)\ f(c)\geq f(x)
$$
です。
つまり、\(\displaystyle\epsilon=\frac{a+b}{2}\)としたとして、\(|x-c|<\epsilon\)を満たすような\(x\in I\)に対しても、\(f(c)\geq f(c)\)が成り立っています。
故に\(f(c)\)は極大値です。
同様に、\(c\in(a,b)\)で最小値\(f(c)\)を取る場合、\(f(c)\)は\(I\)での最小値ですので、
$$
(\forall x\in I)\ f(c)\leq f(x)
$$
です。
つまり、\(\displaystyle\epsilon=\frac{a+b}{2}\)としたとして、\(|x-c|<\epsilon\)を満たすような\(x\in I\)に対しても、\(f(c)\leq f(c)\)が成り立っています。
故に\(f(c)\)は極小値です。
以上のことから、\(x=c\)で極値を取るわけですので命題1.の仮定を満たします。
従って、命題1.により\(f^\prime(c)=0\)です。
故にロルの定理が成り立ちます。
ロルの定理の証明終わり
結
今回は極値(極大値、極小値)とロルの定理とその証明を説明しました。
極大値、極小値はそれぞれ最大値、最小値とは異なりますが一致することもあります。
つまり、最大値かつ極大値であるような定義域内の点が存在することもあれば、最小値かつ極小値であるような定義域内の点が存在することもあります。
しかし、必ず一致するわけではないということに注意してください。
ロルの定理は平たく言えば、
ということでした。
この定理の証明にはワイエルシュトラスの最大値定理を使うことで最大値と最小値の存在を担保し、この場合はその最大値と最小値がそれぞれ極大値と極小値と一致するので、微分係数が\(0\)ですよ、という流れでした。
次回はこのロルの定理を使って平均値の定理のイメージとその証明を与えます。
乞うご期待!
質問、コメントなどお待ちしております!




コメントをする