【挑戦】(数セミ)エレガントな解答をもとむを解く㉙

本記事の内容

本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題を1時間で解けるか、という挑戦をする記事です。

本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。

今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。

前回の問題については以下の記事を御覧ください！

【挑戦】(数セミ)エレガントな解答をもとむを解く㉘

...

for-spring.com

2023.02.20

問題を明示します。

数列\(\{a_n\}_{n\in\mathbb{N}}\)は以下の漸化式で定義されるとします。
\begin{eqnarray}
&&a_{n+3}=-a_{n+2}+2a_{n+1}+8a_n\\
&&a_1=a_2=a_3=1
\end{eqnarray}
　この\(a_n\)がすべての\(n\)について平方数(整数の\(2\)乗)となることを証明してください。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p23.

チャレンジの結果は…？

チャレンジの結果…解けました。
これは隣接四項間漸化式の解き方を知っていれば、ちょっとのヒラメキで解けます。

筆者の解答を紹介します。

数列\(\{a_n\}_{n\in\mathbb{N}}\)の一般項を求めること自体は単純な隣接四項間漸化式の問題のため、大したことではありません。

隣接四項間漸化式
\begin{eqnarray}
\begin{cases}
a_{n+3}=-a_{n+2}+2a_{n+1}+8a_n\\
a_1=a_2=a_3=1
\end{cases}
\end{eqnarray}
の特性方程式は
$$
\lambda^3+\lambda^2-2\lambda-8=0
$$
です。

\(\lambda=2\)とすれば、
$$
8+4-4-8=0
$$
となるため、多項式\(\lambda^3+\lambda^2-2\lambda-8\)は\((\lambda-2)\)を因数に持ちます。

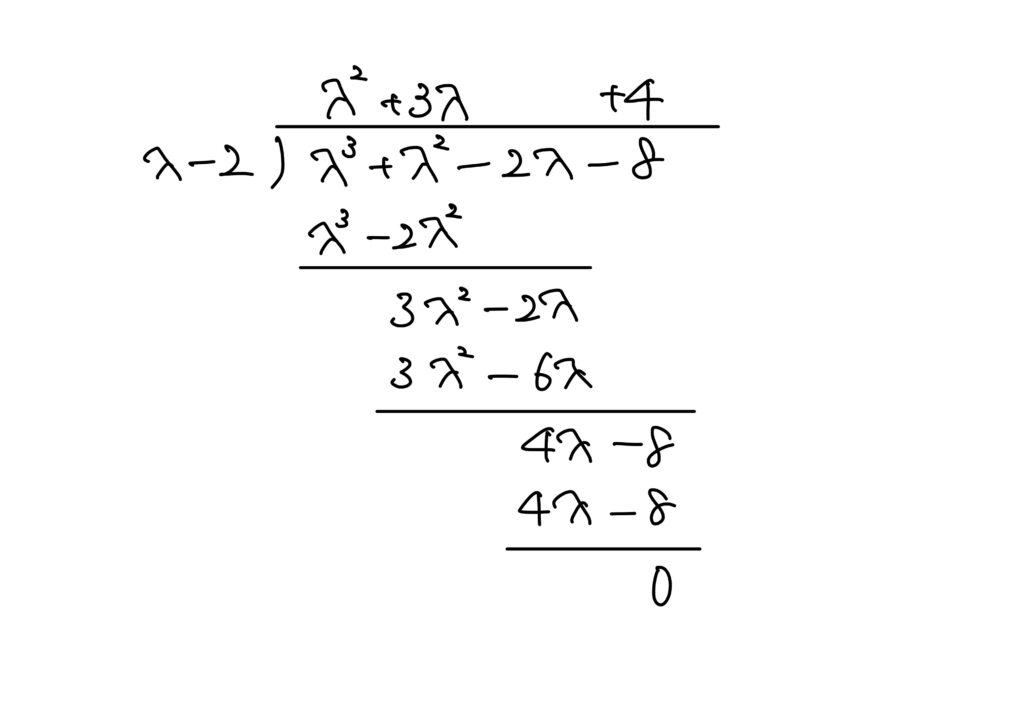
故に、求める\(\lambda\)は
$$
\lambda^3+\lambda^2-2\lambda-8=(\lambda-2)(\lambda^2+3\lambda+4)
$$
を満たす\(\lambda\)となります。
したがって、
$$
\lambda=2,\quad \frac{-3+\sqrt{7}i}{2},\quad \frac{-3-\sqrt{7}i}{2}
$$
です。
ここで、
$$
\begin{cases}
\alpha=2\\
\displaystyle\beta=\frac{-3+\sqrt{7}i}{2}\\
\displaystyle\gamma=\frac{-3-\sqrt{7}i}{2}
\end{cases}
$$
とすれば、\(\{a_n\}_{n\in\mathbb{N}}\)は
$$
a_n=A\alpha^n+B\beta^n+C\gamma^n
$$
という形をしているので、
$$
a_n=A\cdot2^n+B\beta^n+C\gamma^n
$$
です。

今、\(a_1=a_2=a_3=1\)であるから、\(\beta^2\)と\(\gamma^2\)をそれぞれ計算することで
$$
\begin{cases}
\displaystyle2A+\frac{-3+\sqrt{7}i}{2}B+\frac{-3-\sqrt{7}i}{2}C=1\\
\displaystyle4A+\frac{1-3\sqrt{7}i}{2}B+\frac{1+3\sqrt{7}i}{2}C=1\\
\displaystyle8A+\frac{9+4\sqrt{7}i}{2}B+\frac{9-4\sqrt{7}i}{2}C=1
\end{cases}
$$
という連立方程式が立ちます。
これを解けば(骨が折れますが…)、
$$
\left( A,,B,C\right)=\left( \frac{2}{7},-\frac{1}{7},-\frac{1}{7}\right)
$$
となります。
したがって、
\begin{eqnarray}
a_n&=&\frac{2}{7}\cdot2^n-\frac{1}{7}\beta^n-\frac{1}{7}\gamma^n\\
&=&\frac{1}{7}\left( 2^{n+1}-\beta^n-\gamma^n\right)
\end{eqnarray}
となるわけです。

すなわち、問題は

ということになります。
ここで数分悩みました。
常套手段であろう複素数の共役の性質を使うことが鍵になりそうだな、という安易な考えと、\((\cdot)^2\)という形に変形したいということと、\(\beta\)と\(\gamma\)に\(\sqrt{7}i\)という複素数が出現することから
$$
\omega=\frac{1+\sqrt{7}i}{2}
$$
という複素数に着目してみることにしました。
\(\omega^2\)を計算してみると、
$$
\omega^2=\frac{-3+\sqrt{7}i}{2}=\beta
$$
となりました。
どうやら見立てはあっていた模様です。

同様にして\(\omega^3\)を計算してみましたが、\(\omega^3=5-2\sqrt{7}i\)となり、特に関係はなさそうでした。
「であれば、もしかして\(\overline{\omega}^2\)が\(\gamma\)になってたりして」と思い、\(\overline{\omega}^2\)を計算してみました。
すると
$$
\overline{\omega}^2=\frac{-3-\sqrt{7}i}{2}=\gamma
$$
となり、予想は正しかったようです。

ここで「\(\alpha\)はどうすっかな」となりました。
今までの話から、\(\omega\)と\(\overline{\omega}\)を使えばなんとかなりそうな気がしたので、\(\omega\cdot\overline{\omega}\)を計算してみると、
$$
\omega\cdot\overline{\omega}=2=\alpha
$$
となり、道がひらけました。

今の状況をまとめれば、
$$
\begin{cases}
\omega^2=\beta\\
\overline{\omega}^2=\gamma\\
\omega\cdot\overline{\omega}^2=\alpha=2
\end{cases}
$$
です。
これを見たとき、「ああ、なるほど。\(\left(\omega^n+\overline{\omega}^n \right)^2\)がなにか関係してそうだな」と思いました。
実際に計算してみると、
\begin{eqnarray}
\left( \omega^n+\overline{\omega}^n\right)^2&=&\omega^{2n}+2\omega^n\overline{\omega}^n+\overline{\omega}^{2n}\\
&=&\beta^n+2\cdot2^n+\gamma^n
\end{eqnarray}
となりました。
ちょっと惜しかったです。
符号が違ってました。
\begin{eqnarray}
\left( \omega^n-\overline{\omega}^n\right)^2&=&\omega^{2n}-2\omega^n\overline{\omega}^n+\overline{\omega}^{2n}\\
&=&\beta^n-2\cdot2^n+\gamma^n
\end{eqnarray}
ですので、
\begin{eqnarray}
a_n&=&\frac{1}{7}\left( 2^{n+1}-\beta^n-\gamma^n\right)\\
&=&-\frac{1}{7}\left( \beta^n-2\cdot2^{n}+\gamma^n\right)\\
&=&-\frac{1}{7}\left( \omega^n-\overline{\omega}^n\right)^2\\
&=&\left\{\frac{i}{\sqrt{7}}\left( \omega^n-\overline{\omega}^n\right)\right\}^2
\end{eqnarray}
となります。

さて、新たに
$$
b_n=\left\{\frac{i}{\sqrt{7}}\left( \omega^n-\overline{\omega}^n\right)\right\}^2
$$
とすると、問題は、

ということになります。
先程より難度が下がった気がします。

ここで、\(\omega\)に対してもっと情報はないかな？と考えました。
すると、実は\(\omega\)は二次方程式\(\lambda^2-\lambda+2=0\)の解であることがわかりました。
なぜ分かったかと言うと単に\(\left( x-\omega\right)(x-\overline{\omega})\)を展開してみたからです。

さて、\(\omega\)は二次方程式\(\lambda^2-\lambda+2=0\)の解であることから、この二次方程式を特性方程式として見ることで、\(b_n\)は次の隣接三項間漸化式を満たすということがわかります。
$$
b_{n+2}-b_{n+1}+2b_n=0
$$
この漸化式から\(b_1=b_2=-1\)だとわかります。
ということは、\(b_1,b_2\in\mathbb{Z}\)で、任意の\(n\in\mathbb{N}\)で\(b_{n+2}-b_{n+1}+2b_n=0\)を満たすわけですから、任意の\(n\in\mathbb{N}\)に対して\(b_n\in\mathbb{Z}\)ということが分かるわけです。

投稿されたエレガントな解答

筆者は愚直に解いたため、出題者が用意している解答と似ている部分がありましたが、それについては省きます。

（前略）

$$
\lambda=2,\quad \alpha,\quad \beta\quad \left( \alpha=\frac{-3+\sqrt{7}i}{2},\
\beta=\frac{-3-\sqrt{7}i}{2}\right)
$$

（中略）

$$
\frac{1}{7}\left\{ 2^{n+1}-\beta^n-\gamma^n\right\}\tag{1}
$$
ここで、\(\displaystyle\gamma=\frac{1+\sqrt{7}}{2}\)、\(\displaystyle\delta=\frac{1-\sqrt{7}}{2}\)とおくと
$$
\gamma^2=\alpha,\quad \delta^2=\beta,\quad \gamma\delta=2
$$
となるので、
$$
a_n=\left\{\frac{i}{\sqrt{7}}\delta^n-\frac{i}{\sqrt{7}}\gamma^n\right\}\tag{2}
$$
とかける。

（中略）

$$
b_n=\frac{i}{\sqrt{7}}\left( \delta^n-\gamma^n\right)\tag{4}
$$

（中略）

　ところが、\(b_n\)が(4)をみたすことを知ってしまえば実は漸化式を説かなくて良いと気づきます。(4)で\(b_n\)を定義すれば、\(b_n^2=a_n\)が帰納法で示せるのです。たとえば（中略）しは以下のように計算しました。
　\(b_n^2=a_n\)、\(b_{n+1}^2=a_{n+1}\)、\(b_{n+2}^2=a_{n+2}\)を仮定すると
\begin{eqnarray}
a_{n+3}&=&-a_{n+2}+2a_{n+1}+8a_n\\
&=&-b_{n+2}^2+2b_{n+1}^2+8b_n^2\\
&=&-b_{n+2}^2+2b_{n+1}^2+2(b_{n+1}-b_{n+2})^2\\
&=&(b_{n+2}-2b_{n+1})^2=b_{n+3}^2
\end{eqnarray}
幽霊の正体みたりナントヤラ、ですね。この\(b_n\)は
$$
1,\quad 1,\quad ,-1,\quad -3,\quad 5,\quad 7,\quad -3,\quad \cdots
$$
ですから、\(a_n\)の平方根のうち適度に正負を振り分ければ\(b_n\)がみつあるのですが、それは無理というものでしょう。性の平方根だけでなんとかしようとした方々は、\(\ ({\rm mod}\ 3)\)、\(\ ({\rm mod}\ 5)\)、\(\ ({\rm mod}\ 7)\)等で分類されていました。
　また複素根を極座標表示して、3角関数へ持ち込み、チェビシェフ多項式との関連を指摘してくださった方々もおりました。出題者の予期せぬ出会いでした。
　一般化としては、（中略）氏が同じ拡張を教えて下さいました。
　\(b_{n+2}=\alpha b_{n+1}+\beta b_n\)に対し、\(a_n\)を
$$
\begin{cases}
a_{n+3}=(\alpha^2+\beta)a_{n+2}+(\alpha^2+\beta)\beta a_{n+1}-\beta^3a_n\\
a_1=b_1^2,\quad a_2=b_2^2,\quad a_1=(\alpha b_2+\beta b_1)^2
\end{cases}
$$
で定義すると、\(a_n=b_n^2\)がわかります。
　また、（中略）氏は以下のような漸化式をみつけてくれました。
\begin{eqnarray}
&&b_{n+3}^2=-b_{n+1}^2+2b_{n+1}^2+48b_{n+1}b_n+32b_n^2\\
&&b_1=b_2=b_3=1
\end{eqnarray}
こうすると、\(b_i\)は整数であるばかりでなく、平方数であるという恐るべき性質を持っています。(つまり右辺を計算すると必ず4乗数になる！)しかけは簡単ですが、胸がドキドキする拡張でした。

最後にこれまでとまったく異なるアプローチの解答を紹介することにしましょう。

（中略）

数列\(\gamma_n\)を
$$
\gamma_{n+2}=\frac{2^n-\gamma_{n+1}^2}{\gamma_n},\quad \gamma_1=\gamma_2=1
$$
で定義すると、この数列\(\gamma_n\)が以下をみたすことを帰納法で示しました。

1. \(\gamma_n\)は奇数、特に\(\gamma_n\neq0\)。
2. \(\gamma_n=3\gamma_{n-2}-4\gamma_{n-4}\quad (n\geq 5)\)
3. \(\gamma_n^2+3\gamma_{n-1}^2+4\gamma_{n-2}^2=2^n\quad (n\geq 3)\)
   (証明は、少々工夫した計算が必要)

すると3.を用いて、
$$
2(\gamma_k^2+3\gamma_{k-1}^2+4\gamma_{k-2}^2)=\gamma_{k+1}^2+3\gamma_k^2+4\gamma_{k-1}^2
$$
整理して、\(\gamma_{k+1}^2=-\gamma_k^2+2\gamma_{k-1}^2+8\gamma_{k-2}^2\)。
　これと\(\gamma_1=\gamma_2=\gamma_3=1\)から\(a_n=\gamma_n^2\)が得られます。

（中略）

もっともユニークで、もっとも筆者好みの解答は、（中略）から寄せられました。
　（中略）氏は次の関係式を帰納法で示しました。
$$
(a_{n+3}-a_{n+2})^2=64a_{n+1}a_n
$$
するとこの式から\(a_n\)が平方数であれば、\(a_{n+1}\)も平方数であることがわかります。

（後略）

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p195-p198.

読者の皆様への挑戦状！

今から紹介する問題の解答は来週の日曜日に挑戦します！

次の数列は有名なフィボナッチ数列です。
$$
1,1,2,3,5,8,13,21,34,55,\cdots
$$
これは最初の項を\(a_0\)とすると、\(a_0=a_1=1\)、\(n>1\)の一般項\(a_n\)は
$$
a_n=a_{n-1}+a_{n-2}
$$
と表すことができます。つまり、一般項は直前の2つの項の和というわけです。では、
\begin{eqnarray}
&&1,1,2,3,3,4,5,5,6,6,6,8,8,8,10,9,10,11,11,12,12,\\
&&12,12,16,14,14,16,16,16,16,20,17,17,20,21,19,\cdots
\end{eqnarray}
という数列の一般項はどう表現されるでしょう？

（ヒント）フィボナッチ数列ほど単純ではありませんが、最初の\(a_0=a_1=1\)は同じで、\(a_n\ (n>1)\)はそれまでに出てきた2つの項の和になっています。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p23.

前回の問題は【１時間チャレンジシリーズ】挑戦㉘を御覧ください！

結

いかがでしたか？
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。

読者の皆様も是非一度挑戦してみて下さい！
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい！

質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない！」などいただければお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ一週間ほどでお答えします。
(難しかったらもう少しかかるかもしれませんが…)

Twitterでもリプ、DM問わず質問、コメントを大募集しております！

他の「エレガントな解答をもとむ」の問題に挑戦してみたい方はぜひ以下の書籍をお買い求め下さい！